基于两端不确定性的再制造供应链优化*

□ 黄静文 □ 周 敏

1.武汉科技大学冶金装备及其控制教育部重点实验室 武汉 430081 2.武汉科技大学机械传动与制造工程湖北省重点实验室 武汉 430081 3.武汉科技大学精密制造研究院 武汉 430081

1 研究背景

在国家实施中国制造2025的战略背景下[1],再制造是中国制造业未来的发展方向之一。再制造是以经济、节能、环保等作为准则,对废旧产品实施修复的一系列技术措施和工程活动的总称。发展再制造有利于减少自然资源的消耗,降低环境的污染,符合当今强调低碳经济和环境可持续性发展的要求。

由于废旧产品回收的时间、数量、质量不确定,再加上再制造产品市场需求、销售价格、销售数量的不确定,再制造商在满足客户需求的同时,选择再制造工艺,控制其生产成本和生产周期,获得最大收益,这一直是一个挑战。因此,研究两端不确定的再制造供应链优化问题具有重要意义。

在研究再制造供应链方面,国内外专家主要集中在传统的供应链管理方式下,对于在废旧产品回收和再制造产品市场需求不确定情况下的再制造供应链优化研究较少。Xu Xiaofeng等[2]研究了基于供应链协同问题,以达到最优资源为目标,提出了利用混合智能算法的随机约束数学模型,并进行求解。熊中楷等[3]在研究专利许可下再制造闭环供应链问题,利用收益共享和费用分担契约的方法,优化了闭环供应链系统。邓乾旺等[4]分析了回收质量不确定环境下的三种政策机制对闭环供应链的影响,认为政府补贴和碳税相结合的机制可以更加有效地解决问题。刘广东等[5]研究了在生产成本下,集中和分散供应链在零售价格、直销价格及销售量三个方面的稳定性,比较了两种类型的供应链在生产成本扰动和风险规避存在差异时的定价差异性问题。Ben-Daya等[6]建立了两级闭环供应链下的生产再制造库存系统模型,以持有成本和订购成本为关键参数,进行灵敏度分析,实现最优解决策方案。Reddy等[7]提出了一个两阶段的随机线性模型,通过集成产能和库存决策,构建了按订单制造的混合制造-再制造生产系统。Afshar-Bakeshloo等[8]将产成品以折扣价替代再制造产品,运用试验设计和方差分析研究阈值的影响,研究了随机需求下再制造系统的库存控制问题。韩梅等[9]构建了双重竞争下的定价决策模型,运用数值分析的方法进行求解,为闭环供应链管理提供了指导。Al-Salamah[10]提出一种针对不完全制造工艺和项目的经济订单数量模型,利用模型推导出最佳的经济订货批量。Gong Xiting等[11]研究了混合制造/再制造库存系统,以满足有限规划范围内的随机需求,达到在规划范围内将预期的总折扣成本降至最低的目标。

从上述文献可以看出,基于两端不确定性的再制造产品供应链优化研究较少。因此,需要考虑再制造产品回收和再制造的特性,划分再制造产品多组件质量级别。为满足消费者需求,笔者从供应链整体利益角度出发,建立基于多个暂存区的再制造产品多组件库存模型。面对不确定性的市场需求,以期望利润为目标函数,研究再制造产品的最优利润问题,并列举案例,为再制造企业的供应链优化提供有力的理论支持。

2 再制造供应链模型构建

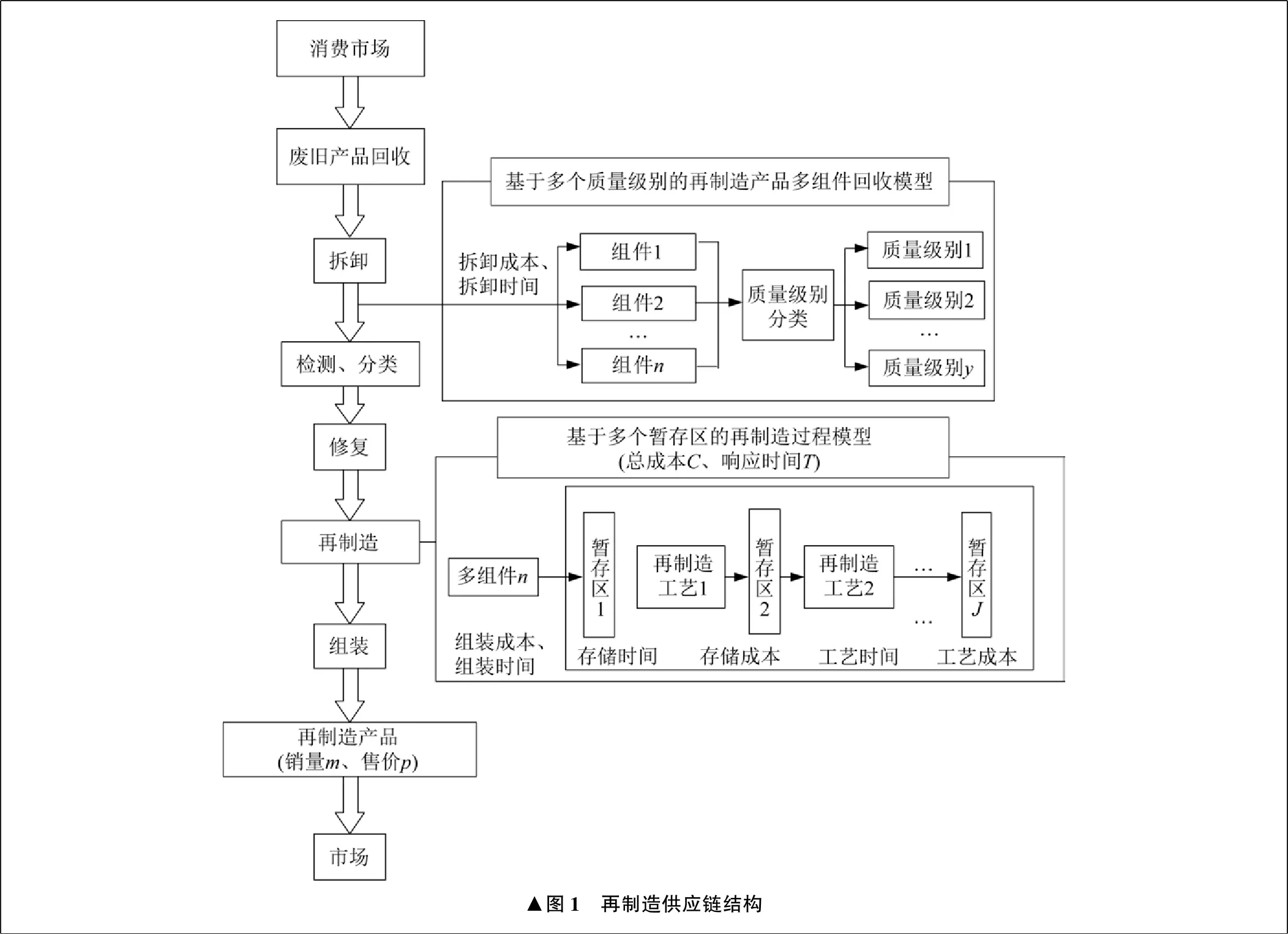
再制造供应链的具体结构如下:① 回收中心从消费市场上回收大量的废旧产品;② 经过回收中心的拆卸、检测、分类、修复等处理工艺;③ 回收后进行拆解的产品分成不同的组件,存储在暂存区中,等待最后一道工艺结束后进行统一的组装;④ 再制造产品通过分销中心向消费市场进行销售。再制造供应链结构如图1所示。

再制造供应链涉及废旧产品回收、拆卸、检测、分类、再制造、组装、再制造产品销售等多个环节[12]。在再制造供应链系统中,再制造产品的销量、售价及废旧产品回收质量是不确定的。因此,进行再制造供应链系统优化研究时,必须要考虑到再制造产品的销量、售价及废旧产品回收质量两端的不确定因素。

由回收不确定性可能会引发库存的不确定性。再制造回收产品的质量级别不同,再制造所需要的加工方式和所花费的时间也不同,同时,存储所需要的存储区级别也不相同,单位成本也不同。单纯地将经再制造工艺的半成品放置在一个暂存区无疑会影响库存成本。

因此,笔者在考虑再制造多级组件的库存时,研究多个暂存区。其再制造过程包含拆解、再制造工艺以及重新组装,回收后进行拆解的产品可以分成不同的组件,存储在暂存区1中,经过每一道再制造工艺后的产品可以依次存储在暂存区2至暂存区j中,等待最后一道工艺结束后进行统一的重组。由于翻新水平下工艺路线的不确定性和加工时间的不确定性,不同组件的单位库存并不相同。

3 再制造产品成本分析

相对于再制造产品而言,传统制造的生产工艺流程几乎是固定不变的,工艺时间的变化不大,响应时间是容易控制的。而再制造产品的回收不确定性因素对其利润变化的影响较大,存在例如回收时间、数量、质量等诸多不确定因素,导致利润预测更加复杂。笔者仅对再制造产品的回收质量不确定性进行研究,使再制造商对利润预测更具前瞻性,并使在不确定性条件下的期望利润达到最优。

3.1 废旧产品的回收成本分析

库存获得成本是指企业为达成订购数量而在自身内部开展各项工作的成本。对于再制造产品而言,库存获得成本就等于其再制造产品的回收成本。

研究库存获得成本有必要考虑再制造产品的回收特性。回收产品经过拆分后得到不同级别的组件,其回收价格不同,回收总成本也不同。某回收产品拆分后存在i个组件,i=1,2,…,n,若根据市场需求回收m件废旧产品,设质量级别为Y类,令废旧产品的回收成本为C1:

(1)

式中:qiy为质量等级为y的组件i的回收价格;μiy为m个回收产品第i个组件拆解成质量级别为y的概率。

▲图1 再制造供应链结构

3.2 再制造产品库存持有成本分析

由于各组件的加工时间和加工顺序不尽相同,因此,各组件库存的持有成本就不相同。

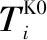
(2)

当i=1,2,…,n时,各个组件从拆解到组装的时间Ti为:

(3)

3.3 制造产品工艺成本分析

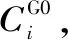
(4)

4 再制造产品市场需求分析

当市场处于完全竞争环境中,再制造产品需求不会间断,市场需求量D与产品价格P、响应时间T之间存在线性函数关系,且市场需求随价格增加而减少。

D=d-b1P-b2Td≥0,b1≥0,b2≥0

(5)

式中:d为供应链基本需求量;b1为市场需求率的价格弹性因数;b2为市场需求率的响应时间弹性因数;T为供应链响应总时间,即供应链中产品交货期。

价格对承诺响应时间敏感,承诺响应时间越长,价格越低,承诺响应时间越短,价格越高。供应链响应时间与产品价格的关系为:

P=P0-hT

(6)

式中:P0为响应时间为0的价格;h为产品价格受供应链响应时间的弹性因数。

由式(6)可以看出,产品价格与响应时间成反比关系,即供应链的响应时间越短,产品价格越高。

将式(5)代入式(6),得:

D=(d-b1P0)+(b1h-b2)T

(7)

5 再制造产品利润预测模型

5.1 再制造产品利润预测模型构建

首先对模型做如下假设:

(1) 拆分后的每个质量级别都可用来再制造,不考虑损坏或过低质量级别的组件;

(2) 废旧组件进行再制造会存储在各个暂存区中,其各组件符合上述的再制造流程;

(3) 将市场需求量D与产品价格P、响应时间T简化为线性函数关系。

一个垄断市场的需求依赖于价格,根据时间安排做出两个决定。第一是确定最优库存数量关于价格的函数,根据最大化期望利润函数,求出最优的售卖价格。第二是根据售卖价格,确定好库存数量。

总成本C为:

C=C1+C2+C3

(8)

令利润函数为I(P,D,T),当D(P,T)>m时,有:

I(P,D,T)=PD(P,T)-C

=(P0-hT)(d-b1P0-b2T+b1hT)

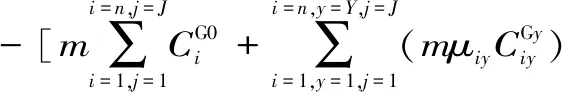
(9)

在销售季开始前,再制造商回收m件废旧商品。如果需求量D不大于m,那么D废旧商品使用再制造产品以单位价格P出售,剩余m-D部分以单位价格a清空。

当D(P,T)≤m时,有:

I(P,D,T)=PD(P,T)-C+[m-D(P,T)]a

=(P0-hT)(d-b1P0-b2T+b1hT)

-b1hT+b2T)a

(10)

5.2 再制造产品利润预测模型求解

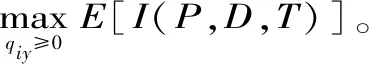
由于期望利润函数是一个关于P和m的二元函数,所以首先找到最优的库存。

E[I(P,D,m)]关于变量T的一阶与二阶偏导为:

+2b2hT-2b1h2T

(11)

(12)

对式(11)求二次导数,可以得到利润有关时间的二次导函数:

(13)

由于有关利润的二元函数中导数小于0,则期望利润函数关于变量T为严格凹函数,即可以确定最大的市场需求量D和价格P,使期望利润函数达到最大,达到再制造供应链的优化目标。

6 案例分析

为验证上述模型的可靠性,以某公司回收的一批再制造发动机产品的利润变化为例,计算最优的再制造产品利润。

某公司回收一批废旧发动机,m为58件,将回收的这批发动机进行拆卸,可拆卸为八类主要组件,其参数值见表1。

表1 八类主要回收组件参数值

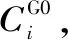
在该公司对再制造发动机进行销售期间,相关参数设定见表2。

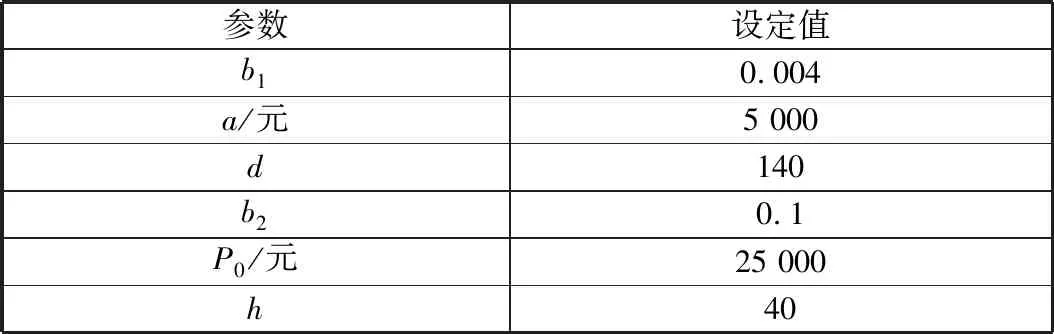
表2 参数设定

基于上述模型,对市场需求进行分析,判断废旧商品的数量m是否会大于市场需求D,代入各参数,计算再制造产品响应总时间T。

经过计算,当市场需求D为43件的时候,计算的总利润I为481 690元,价格P为23 200元/件,再制造周期T为45 d,再制造库存获得成本C1为240 497元,再制造库存持有成本C2为12 992元,再制造工艺成本C3为262 421元,同时,各组件在暂存区1或2的存储时间见表3。

表3 各暂存区存储时间

7 结束语

笔者针对再制造产品回收不确定和市场需求不确定导致的供应链收益不确定问题,研究了再制造产品的回收特性,对回收的多组件划分出不同的质量级别,建立了基于不同质量级别的回收模型。针对不同质量级别的组件再制造工艺和库存成本不同,研究基于多个暂存区的再制造库存。然后以期望利润为目标函数,建立受价格、响应时间影响的再制造产品市场需求模型。根据产品市场需求和废旧产品回收情况,建立利润函数,以利润最大化作为再制造供应链的优化目标,对模型进行求解。最后,以某公司回收一批再制造发动机为例,计算最大利润和最优的库存方案,验证了模型的可行性。

由于该模型只考虑了单个再制造商的决策,在未来的研究中,可以考虑在再制造混合系统下研究再制造产品供应链优化问题。