基于多尺度特征融合的蔬菜价格预测模型研究

刘合兵，韩晶晶,2，庄晨辉,2，郑光,2，席磊,2，张红阳

(1.河南农业大学信息与管理科学学院，河南 郑州 450046；2.农田监测与控制河南省工程实验室，河南 郑州 450046)

农业是关乎国计民生的基础性产业，农产品价格的稳定对中国国民经济具有重要影响。当前，相关价格调控政策主要针对耐存储的大米、小麦、棉花等大宗农产品，涉及具有高度易腐蚀的鲜瓜果蔬菜却少之甚少[1]。现实生活中，蔬菜价格受到市场供需不平衡、种植运输成本、天气变化以及特殊节假日等诸多因素影响，其价格序列表现出频繁的波动性,也为蔬菜价格的预测带来挑战。本研究通过对蔬菜价格进行波动特征分析，开展价格预测研究，可为经营者提供前瞻性信息，调整生产销售思路,也为相关部门提高市场风险规避能力[2]。

围绕农产品价格，国内外开展了广泛研究，目前主要涉及价格的波动特征及其规律的研究、影响因素的研究和价格预测方面的研究。首先，关于价格波动特征及其规律的研究，学者们分别提出关于生产和商品价格的波动，形成蛛网理论的雏形，为农产品价格的研究奠定基础。其次，关于影响因素的研究，供给和需求是影响农产品价格变动的根本原因，其他市场因素、国家政策等均是通过影响供求进而影响农产品价格的波动[3]。最后，普遍关注的就是农产品价格的预测研究，农产品种植受气候限制和影响，再加上特殊节日(如春节、中秋节)等因素，其价格波动具有季节性、趋势性及随机波动性。

目前，主要有计量经济预测法、数理统计预测法、智能模型法和组合预测法4种预测方法。计量经济学旨在揭示经济现象中的因果关系，价格预测中最常用到的就是回归分析法，根据影响农产品价格的因素与价格之间的函数关系建立线性或非线性回归模型[4-5]。由于影响价格变动的因素较多，在预测时并不能一一列举，也并不能一一量化，且不同的影响因素对价格影响的严重程度、持续时间也不同，这就对价格预测工作带来很多不便，制约计量经济学对价格预测的准确度。数理统计预测是统计学的重要功能，也是预测领域最常用到的方法。在农产品市场的价格预测中，应用最广泛的是传统的时间序列预测方法，主要包括季节指数法[6]、移动平均法[7]、指数平滑法[8]等。这些方法处理数据时较为理想化，对于线性特征的时间序列数据预测的精度较高。但是，很多方法涉及模型参数的调整问题，需要研究学者耗费大量时间精力，积累实践经验获取较高的预测精度。此方法在进行预测时，为模型参数调整带来较大困难，反映出一定的局限性，且这些方法在对于非线性的农产品价格预测的实际应用中结果并不太理想。

随着信息技术的快速发展，相对应的智能方法也被应用于各个领域，学者们对农产品价格也应用智能分析方法进行预测，例如神经网络预测法[9-11]、灰色预测法[12-13]、支持向量机[14]等。组合模型[15-23]已成为目前预测领域的热门方向，它可以利用单一模型的预测优势，结合研究对象的实际变化规律，充分挖掘研究对象的特征信息。通过将不同的方法所得的结果进行等权或不等权的组合，或通过辅助方法进行先处理促进后续预测方法预测精度的提升。结果证实组合预测方法充分结合了单一预测方法的优势，表现出更佳的预测精度。

关于价格预测问题的研究，虽然成果颇为丰富，但仍然存在一定的不足。首先，国内外学者大都关注大宗农产品的研究，对蔬菜价格的研究极少，且鲜有针对区域的研究。第二，对于蔬菜价格预测的研究，虽然预测精度很好，但预测方法的应用并不能验证其对多种类的蔬菜预测。第三，对蔬菜价格预测的研究往往跟价格波动特征的分析分割开来，造成价格预测的解释性较差。第四，由于蔬菜价格是受多种因素的影响，且个别影响因素并不能以数据形式量化出来，不同的影响因素对价格的影响时间长短、影响程度也不同。基于以上的思考，本研究对农产品价格进行预测的着眼点为价格数值的研究，在对河南省批发市场的蔬菜进行波动特征分析的基础上，提出多尺度特征融合方法(multi-scale feature fusion，MSFF)，对各个种类的代表性蔬菜分别进行预测研究，揭示其价格波动规律，准确把握未来价格走势。

1 数据与方法

1.1 数据

1.1.1 数据来源 本研究实验数据来自河南省农产品信息监测系统(http://ncpprice.agridoor.com.cn/login.asp)，从中选择某农贸市场马铃薯、莲藕、番茄、黄瓜、大白菜、油麦菜的月均价格。参照数据可获得性和连续性原则，选择2014年1月至2019年12月的等间隔连续数据为样本进行实证分析。其中，根茎类蔬菜代表是马铃薯和莲藕。马铃薯是最有前景的高产作物，也是热门的营养食品。莲藕外表细嫩光滑味甜而脆，药用价值非常高，是一种药食同源的佳品。茄果类蔬菜的代表番茄和黄瓜。番茄清热止渴，富含维生素C，可以补充大量人体需要的元素，且在一年四季均消费量较大。黄瓜清新可口脆嫩鲜美，是夏季最为活跃的一道凉菜。叶菜类蔬菜选择大白菜和油麦菜。大白菜价格相对较低，消费量也大。油麦菜在种植中适应环境的能力比较强，是众多农户种植蔬菜的首要选择，产量相对稳定。

1.1.2 河南省蔬菜价格波动变化 马铃薯、莲藕、番茄、黄瓜、大白菜、油麦菜2014年1月至2019年12月的月均价格波动特征如图1所示。不同种类的蔬菜价格走势各不相同，但均表现出不平稳、非线性波动趋势。从图1中可以看出，莲藕的整体价格均比马铃薯的价格高，且2种蔬菜的价格走势并不一致，莲藕比马铃薯表现出较强的周期波动性，莲藕价格在每年的3月开始上涨至6—8月份时达到最高值，随即开始下跌至波谷，而马铃薯每年的价格走势较为平缓，并未表现出较强的波动性。莲藕在2015年6月的价格最高为8.84元·kg-1,是2017年11月最低价格2.17元·kg-1的4.07倍。马铃薯在2016年4月的价格最高为4.36元·kg-1，最低的价格在2017年7月为1.16元·kg-1，最高价是最低价的3.76倍。可以看出莲藕的月均价格差值大于马铃薯，且马铃薯相比较莲藕易于储存，莲藕表现出较强的周期波动性与其在秋天上市紧密相关。

图1 蔬菜价格变化Fig.1 Changes in vegetable prices

从图1中可以看出，番茄和黄瓜的整体价格相差不大，且相对于根茎菜和叶片菜，番茄和黄瓜表现出较为一致的价格波动特征。番茄和黄瓜的价格从每年的1月份开始慢慢下跌，到5—7月份价格跌落至最小值，接着价格从波谷慢慢上涨至每年的12月至第2年的2月份，价格达到最大值即完成一个新的周期变化。这6年来番茄在2019年2月的价格最高为6.05元·kg-1，是2016年7月最低价格0.94元·kg-1的6.44倍。黄瓜在2019年12月价格最高为6.12元·kg-1，最低价格在2016年6月为0.82元·kg-1，最高价是最低价的7.46倍。可以看出番茄和黄瓜的月均价格最高值和最低值相差较大，且其表现出强烈的周期波动性，这跟番茄和黄瓜都是在每年夏天产出，集中上市阶段供大于求导致番茄和黄瓜的价格较低。

从图1中可以看出，油麦菜的整体价格比大白菜的高，虽然这2种蔬菜的价格走势并不雷同，但都表现出一定的波动频率和幅度。在这6年时间内油麦菜波动次数比大白菜次数多，且波动幅度也比较大。油麦菜在2017年9月价格最高为6.67元·kg-1，是2014年4月最低价格0.93元·kg-1的7.17倍。大白菜在2016年3月价格最高为2.62元·kg-1，最低价格在2018年12月为0.49元·kg-1，最高价是最低价的5.35倍。可以看出油麦菜的月均价格差值大于白菜，大白菜的价格波动较小，主要是由于目前大多数的大白菜属于大棚作物，一年四季均可种植，受气候影响较小。

1.2 方法

1.2.1 价格预测方法 在预测研究中，不论是时间序列预测模型还是智能预测模型，都会涉及模型参数的反复调整问题。参数的设置需要研究原始序列的波动特征，依据其特征，花费大量的时间精力积累实践经验进行调整才能获得较好的预测结果。本研究利用经验模态分解(empirical mode decomposition，EMD)和极限学习机(extreme learning machine，ELM)的优势进行组合预测研究。EMD是一种适用于非线性、非平稳时间序列的信号分解方法。它可以根据信号本身的特征对其自行分解，分解前不需要设置任何基函数，可以根据序列特征自行分解出本征模态函数(intrinsic mode function，IMF)和余项，IMF的数量是根据原序列特定产生的。极限学习机(extreme learning machine，ELM)在建立预测模型时只需要设置好隐含层神经元的个数即可，该方法克服了传统神经网络需要设置大量参数的缺点，且具有学习效率快、预测结果佳的优势。

本研究提出的多尺度特征融合的预测模型具体流程如图2所示，根据蔬菜的价格时间序列利用EMD进行分解，得出若干个IMF和一个线性余项分量。其中，对IMF1进行小波变换分解出近似序列和细节序列，对分解出的多尺度分量分别用极限学习机建立预测模型，最后将各个分量的预测结果进行累加融合得到最终预测值。

多尺度特征融合模型将单一的非线性非平稳的时间序列分解成具有一定周期波动规律的多尺度特征分量，对这些多尺度特征分量分别建立独立的预测模型，这些预测模型是价格序列的重要组成部分，但各分量又相互独立，结合不同分量预测模型的特征优势对其进行累加融合得到最终的蔬菜价格预测值。

图2 蔬菜价格预测流程图 Fig.2 Vegetable price forecast flow chart

1.2.2 结果评价方法 选择平均绝对误差(MAE)、平均百分比误差(MAPE)与均方根误差(RMSE)指标来度量预测模型的精度。各指标的公式如下:

(1)

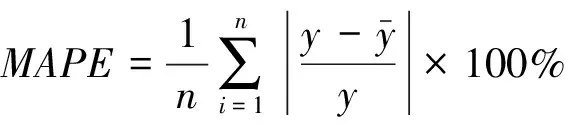
(2)

(3)

2 多尺度特征融合模型构建

2.1 经验模态分解

EMD是一种适用于非线性、非平稳时间序列的信号分解方法，根据信号本身的特征对其自行分解，分解前不需要设置任何基函数，这是它从根本上摆脱了傅里叶变换理论的束缚，也是与傅里叶分解和小波分解的本质区别。它将原始序列分解为若干个本征模态函数和一个剩余分量。

经验模态分解步骤如下：

(1)取原始序列x(t)的所有极大值和极小值。

(2)分别通过3次样条函数拟合出极大值、极小值的上包络线xmax(t)和下包络线xmin(t)，计算上下包络线的均值m1(t)，即

m1(t)=[xmax(t)+xmin(t)]÷2

(4)

(3)计算x(t)与m1(t)之差，记为h1(t)，即h1(t)=x(t)-m1(t)，如果h1(t)满足IMF的条件，则记为c1(t)=h1(t)，c1(t)就是第一个IMF分量；如果h1(t)不是IMF，则将h1(t)视为新的信号x(t)，重复以上步骤直到h1(t)是一个IMF，记为c1(t)。

2.2 小波变换

20世纪80年代，真正意义的小波变换概念被提出。它能够对信号进行多尺度分解，在分解过程中能够充分突出信号的细节特征，在信号高频部分进行时间细分，在低频部分进行频率细分，从而达到聚焦信号细节特征的作用，实现对分析对象更为细致的逼近，提高对信号细节信息的分析处理能力。

小波变换能够有效地反映信号的局部信息，是一种处理非平稳信号的好工具。在实际生活中采集到的数据往往是离散的，因此对于连续小波变换理论而言，主要应用于对理论层面上的分析，难以直接应用于实际中。小波变换的数学表达式为：

(5)

式中:α为尺度因子，τ为平移量，f(t)为基本小波。在应用中，小波分解结果的好坏依赖于小波函数的选择。满足小波定义要求的函数均可被称作为小波函数，这也使得小波函数的种类多种多样，选取不同的小波函数得到的信号处理结果不同。

2.3 极限学习机

ELM作为一种新型的单隐层神经网络，其网络结构包括输入层、输出层和一个隐含层。它可以用最简单的线性回归得到满意的解，大大提高训练速度，解决了传统前馈神经网络训练速度慢、网络参数多次迭代更新、易陷入局部最优等问题。在训练之前，只需要设置适当的隐含层节点数，随机为输入权重和隐含层偏置进行赋值，然后通过最小二乘法得到输出层权值。它不需要多次迭代，也不需要在迭代中确定参数，从而大大降低了计算量和搜索空间。

假设有N个任意的样本(xi,yi)，其中xi=[xi1,xi2,…,xin]T∈Rn为输入向量，yi=[yi1,yi2,…yim]T∈Rm为输出向量。对于一个有L个隐含层节点的神经网络可以表示为：

(6)

式中：j=1,2,……,N,，Wi=[Wi1,Wi2,…,Win]T是连接第i个隐含层节点和输入节点的权重，bi是第i个隐含层节点的偏置，βi=[βi1,βi2,…,βim]T是第i个隐含层节点和输出节点之间的权重。g(x)是激活函数。如果该神经网络能以零误差逼近训练样本，则N个方程的矩阵形式可写为Hβ=Y，其中H是隐含层的输出矩阵，Y是目标输出矩阵。

ELM在训练过程中已经转化成求解方程最小值的最优化问题。极限学习机所得解是唯一最优解，保证了网络泛化能力，且学习速度快[24]。在保证较好的预测结果前提下，其优异的训练速度为其自身与其他方法结合提供了便利，越来越引起各个领域的高度关注和深入研究。

3 多尺度特征融合模型应用实例

3.1 预测模型应用

蔬菜价格的变化图表现出不平稳、非线性特征。EMD可以利用MATLAB编写程序将序列分解为若干个IMF和余量,结果如图3所示。图3中第一曲线图为各个蔬菜的原始序列图，中间为IMF分量图，最后一个为余量图。可以发现，原始的价格序列通过经验模态分解后，不同种类的蔬菜呈现出不同的分量波动特征，菠菜的IMF分量最多，为5个。其次是马铃薯和莲藕的IMF分量为4个，番茄、黄瓜和大白菜的IMF数量最少，为3个。其中，每种蔬菜的本征模态函数分量中IMF1分量跟原始价格相比，波动幅度有明显的下降，波动频率有所增加。IMF2分量与IMF1分量相比，波动频率明显减少，波动幅度与原始价格序列的波动幅度较为相似。最后几个IMF分量波动缓慢且有规律，余量与原序列整体走向一致，反映其线性趋势。从整体的分量图看，IMF1分量依然波动剧烈，且其序列的不平稳、非线性特征严重影响后续的预测精度。

图3 蔬菜价格序列及EMD分量Fig.3 Vegetable price series and EMD components

针对农产品价格预测提出的多尺度特征融合模型中涉及2种不同的分解技术，即经验模态分解和小波变换。特别是经验模态分解被选为主要的分解方法，充分利用了它能够根据非线性信号其自身特征自行分解出几个IMF和余项。然而，EMD分解产生的IMF1依然具有强烈的非线性和不规则特征。根据文献[25]所述原始序列的非线性越高，IMF1就越不规则，且IMF1的数值总是如此之小。虽然它对模型拟合贡献不大，但将导致后续预测难度的增加，对时间序列的预测精度有着很大的干扰。在文献[26]的记载中证实将IMF1从本征模态函数分量的集合中剔除，预测精度略有提升。

针对IMF1分量分解后依旧波动剧烈问题提出多尺度分解方法，即利用小波变换对每个种类蔬菜的IMF1进行再次分解。根据IMF1分量的具体波动特征，采用Daubechies小波基函数(简称dbN，N为小波的阶数)，选择阶数为5，对IMF1分量进行去噪处理。模型选择小波变换的分解尺度为2，可以避免分解尺度过小不利于细节特征的突出，分解尺度过大加重实践操作的弊端，即对IMF1进行db5的2尺度分解得到趋势低频部分a2及细节高频部分d1、d2，对其波动的频率和幅度进行更为细致的透视，分解过程如图4所示。

蔬菜价格经过多尺度分解后得到多个序列分量，分别MATLAB编写程序运用ELM对其每个分量建立预测模型，将2014年至2018年月均价格数据作为训练集，分解出的2019年的数据作为测试集。在预测过程中为了获得较高的预测精度，预先对分量序列进行归一化处理。由于蔬菜价格具有强烈的季节波动特征，每年对应月份的价格波动具有一定的相似性。因此，设置神经网络时选用当前6个月的价格和上一年同月份的价格共7个数据作为输入层数据进行提前一步预测，其输入输出的构成如图5所示。在隐含层神经元个数的设定时，考虑到研究序列的长度，构建从3至25的预测模型，对每个模型在预测时重复训练15次，选取绝对误差最小的预测模型。隐含层神经元的个数根据不同分量的波动特征经过实践选择不同的数值。对输出数据进行反归一化处理，最后对各个分量的预测值进行累加融合得到预测值。

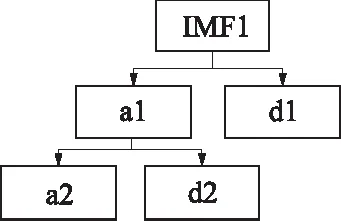
图4 IMF1小波分解示意图 Fig.4 IMF1 wavelet decomposition diagram

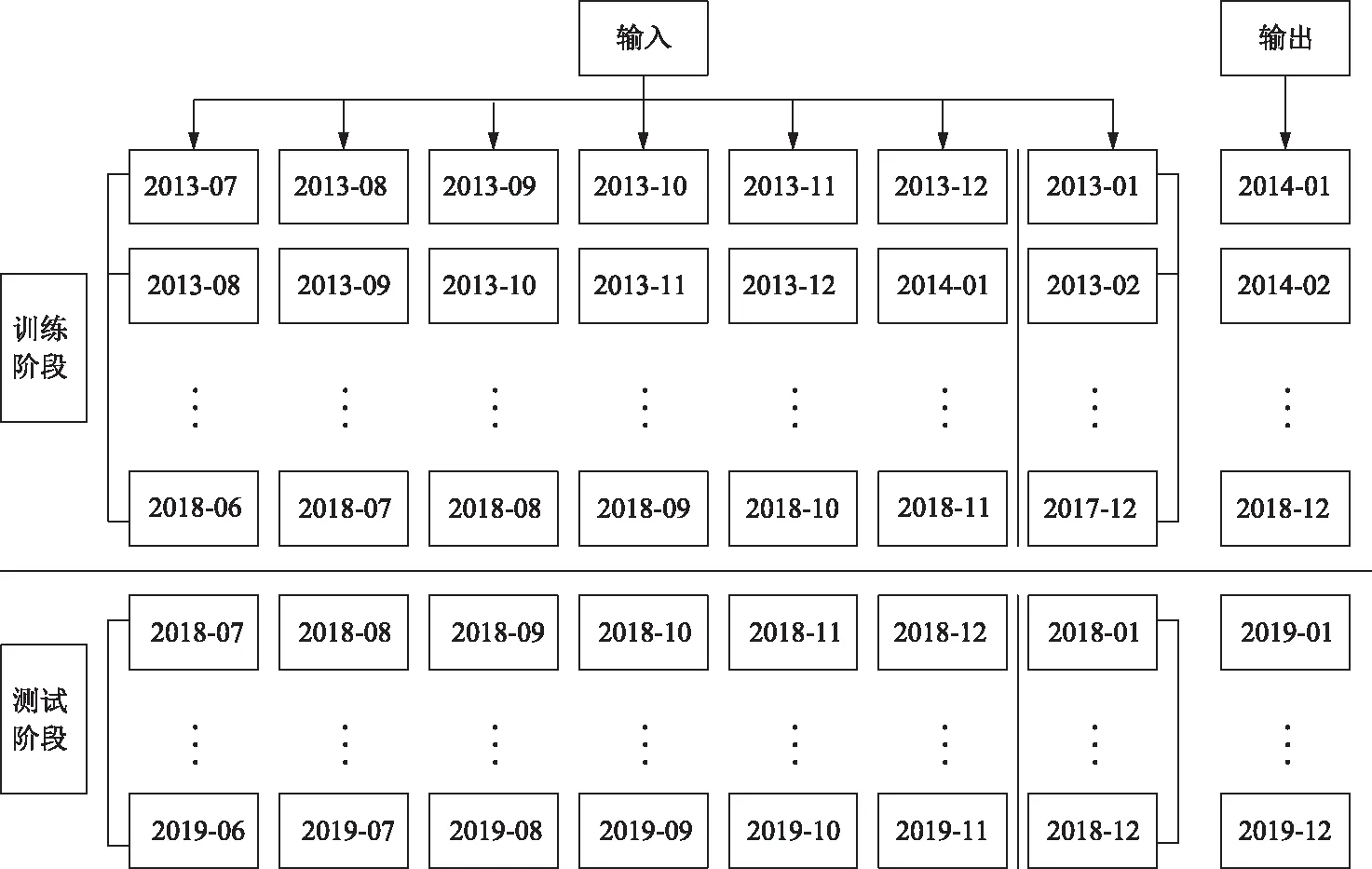
图5 ELM的输入和输出数据构成 Fig.5 ELM input and output data composition

3.2 结果分析

为了分析多尺度特征融合模型的预测性能，分别对根茎菜(以马铃薯和莲藕为例)、茄果菜(以番茄和黄瓜为例)以及叶片菜(以大白菜和油麦菜为例)应用预测模型，与EMD-ELM组合模型进行比较，预测精度评价指标分析结果如表1所示。EMD-ELM组合模型在预测时选择与多尺度特征融合模型同样的操作步骤，主要为ELM建模的相关操作步骤即先对各序列进行归一化处理，选择当前6个月的价格和上一年同月份的价格共7个数据作为输入层数据进行提前一步预测，最后对预测数据进行反归一化处理，进行累加得到预测值。从表中可以看出，基于多尺度特征融合的预测模型的预测精度较好。由于对原始的蔬菜价格序列用经验模态分解方法进行了分解，并针对IMF1用小波变换再次分解，分解后的多尺度分量有效降低了后续预测过程的复杂度。图6为6种蔬菜价格2019年12个月份经过多尺度特征融合方法得到的预测值与实际值的拟合图，从图中可以看出其预测值与实际值的拟合情况基本吻合，整体来看茄果菜表现最好，预测值与实际值的整体重合度最高。

基于多尺度特征融合的预测模型实际应用于河南省马铃薯、莲藕、番茄、黄瓜、大白菜、油麦菜的月均价格进行预测。结果表明，马铃薯、莲藕、番茄、黄瓜、大白菜、油麦菜平均绝对误差分别为0.06、0.25、 0.14、0.19、0.04、0.17 元·kg-1,平均百分比误差为2.70%、4.58%、4.71%、4.76%、3.90%、3.84%，均方根误差为0.08、0.37、0.17、0.26、0.05、0.21。且其平均绝对误差、平均百分比误差和均方根误差均比EMD-ELM组合模型的预测结果表现好。综合对比可以看出，3个精度评价指标中根茎菜中马铃薯和叶片菜中大白菜数值最小，模型预测结果表现最佳。参照蔬菜价格的走势图可以看出马铃薯和大白菜的价格跟其他4种蔬菜相比，其价格数值区间大部分在0～3元·kg-1的低价位区间，且对比其他种类的蔬菜波动情况，马铃薯和大白菜的波动幅度最小，因此在预测模型的应用中预测评价指标表现最好。莲藕的价格数值区间跟其他种类的蔬菜相比最大，具有强烈的波动特征，因此平均绝对误差和均方根误差的数值最大，相对于其他蔬菜的预测精度表现较差。

表1 蔬菜价格预测结果对比 Table 1 Comparison of vegetable price forecast results

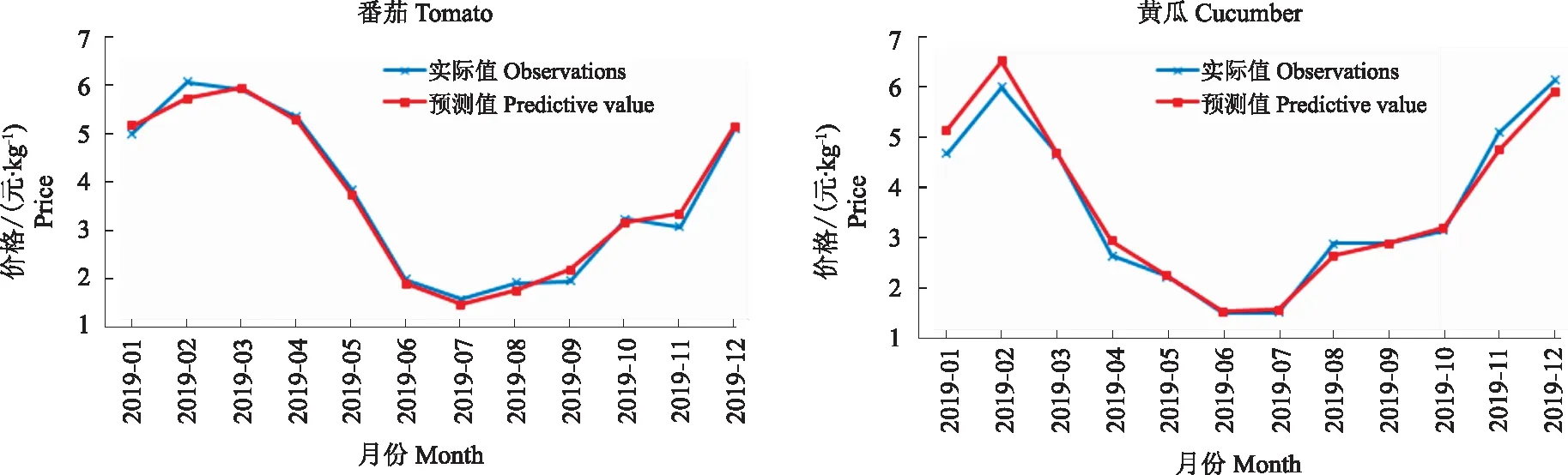
图6 蔬菜价格预测拟合Fig.6 Fitting diagram of vegetable price forecast

4 结论

本研究以河南省为特定区域，在分析根茎类、茄果类和叶菜类的代表性蔬菜的价格波动趋势的基础上，针对蔬菜价格的非线性波动形态，采用经验模态分解、小波变换和极限学习机，提出一种多尺度特征融合的预测模型，并对根茎类、茄果类及叶菜类的代表性蔬菜进行预测研究，对其结果进行预测精度的指标度量。

1)通过对根茎类、茄果类和叶菜类的代表性蔬菜进行波动特征分析，得出不同种类的蔬菜价格波动特征不同，其中茄果类的代表番茄和黄瓜整体波动特征较为一致。蔬菜价格的波动周期基本跟产出时间节点相关。

2)蔬菜的价格序列通过EMD分解出不同的IMF分量及剩余分量。IMF分量的数量与蔬菜价格的原始序列相关，从各分量的展示图中得出IMF1分量虽然有效地降低了原始序列的波动幅度，但仍存在分量波动频繁的特征。

3)基于IMF1分量仍存在波动频繁特征，提出多尺度特征融合预测模型，将其预测结果与EMD-ELM模型进行对比，表明预测结果在MAE、MAPE及RMSE3个指标中均比EMD-ELM的组合模型表现好，说明对IMF1利用小波变换做再次分解能有效降低时间序列的非平稳性，有利于后续预测精度的提高。实验证实蔬菜价格的波动幅度和频率影响价格的预测精度。

本研究提出的多尺度特征融合的预测模型，结果表明经验模态分解和小波变换对原序列做分解可以兼顾序列的时序性和非线性特点，极限学习机又能深入挖掘序列隐含的某些特征，得出较好的预测精度。该方法能够为非线性复杂的价格短期精准预测提供一种新的思路，为未来价格走势做出模拟。但是本研究在进行分析和预测时，选取蔬菜为代表，为进一步验证方法的普适性，还需对其他地域、其他种类的农产品做进一步尝试。