不同ET0计算方法在华北土石山区的适用性评价

蒋丽娅, 陈静, 桑玉强, 贾长荣, 何春霞, 张劲松

(1.河南农业大学林学院, 河南 郑州450002；2.济源市林业工作站，河南 济源 459000;3.中国林业科学研究院林业研究所/国家林业局林木培育重点实验室,北京100091)

参考作物蒸散量(reference crop evapotranspiration，ET0)为“假设作物高度为0.12 m，冠层阻力为70 s·m-1，反照率为0.23的参考冠层的蒸散量，相当于生长旺盛、长势一致、完全覆盖地面且水分供应充足的开阔绿色草地的蒸散量”[1]，是水文循环过程中的重要参数[2]，也是计算作物需水量的关键因子。准确计算ET0对区域内的水资源规划、水资源管理具有重要意义，尤其是在指导作物灌溉方面发挥着重要作用[3-4]。根据所需要的气象参数不同，ET0计算方法大致可分为3类，分别为综合法、辐射法和温度法[5]。由于各方法因地域限制难以得到大范围推广，联合国粮农组织(International Food and Agriculture Organization， FAO)推荐使用综合法中的Penman-Monteith方法(PM方法)作为计算ET0的标准方法和评估其他方法的标准方法[1]。该方法基于能量平衡和空气动力学原理，较全面地考虑了影响蒸散的各种因素，在气候差异较大的区域也取得了令人满意的结果，具有普遍适用性[6-7]。但该方法需要太阳辐射、温度、相对湿度、风速、日照时数等多个气象数据，且计算过程复杂，很多地区难以同时获得这些数据，从而制约了该方法的推广[8]。为了能在气象资料不足的条件下也能较准确地计算出ET0，找到一种更简便的方法代替PM方法是十分有必要的。

近些年，国内外学者以Penman-Monteith方法为标准，对多种ET0计算方法的适用性进行了评价[8-15]，发现不同计算方法适用性的地域差异较大。如尹春艳等[9]、GAO等[10]、魏光辉等[11]分别发现Priestley-Taylor方法在黄河三角洲湿润地区、新疆阿克苏、新疆焉耆盆地的适用性较好。姜梦琪等[12]、魏宾[13]、GAO等[10]、黄彩霞等[14]发现，Hargreaves方法在鄂尔多斯乌审旗地区[12]、新疆车尔臣河流域[13]、陕西铜川、甘肃中东部等干旱半干旱地区的适用性最好。徐冰等[15]发现，Irmark-Allen方法则在西藏高寒牧区更适用。闫浩芳等[16]发现，FAO Penman 法更适合内蒙古河套灌区；LU等[17]则发现，Priestly-Taylor方法、Turc方法和Hamon方法在美国湿润的东南部适用性较好。说明不同ET0计算方法在不同地区、不同气候条件下适用性存在一定的差异。目前，前人对ET0的研究较少，多集中在西北干旱半干旱地区、四川盆地湿润地区、黄河中游干旱半干旱地区，涉及华北地区相对较少[4]。华北土石山区是华北平原重要的生态安全屏障，其南端紧邻黄河，在黄河流域生态保护和高质量发展中发挥着重要作用。因此，科学评价和确定ET0计算方法对当地的水资源管理与利用至关重要。本研究以Penman-Monteith方法的计算结果为标准，分别选择了辐射法中的Priestley-Taylor方法和Irmark-Allen方法，温度法中的Hargreaves方法和Mc Clound方法，综合法中的Penman1963方法，对其进行评价，分析这5种方法在华北土石山区的适用性，为缺乏气象数据的条件下计算该地区的ET0提供依据。

1 材料与方法

1.1 研究区概况及数据资料

研究区为河南黄河小浪底地球关键带国家野外科学观测研究站(35°01′45″N，112°28′08″E)，位于河南省济源市境内，地处华北土石山区的太行山南麓，是典型的低山丘陵区。海拔在400 m左右，属暖温带大陆性季风气候，主要植被类型为暖温带落叶阔叶林及针阔混交林等。土壤成分为棕壤和石灰岩风化母质淋溶性褐土，土壤结构不良，石砾含量10%～18%，土层厚度小于50 cm。全年平均日照时数为2 368 h，0 ℃以上年均有效积温为5 282 ℃·d，年均气温12.4～14.3 ℃。年均降水量641.7 mm，降水季节分配不均，6—8月平均降水量438.0 mm，占全年降水量68.3%，年均蒸发量1 611.2 mm[18]。

因该地区作物主要生长月份集中在5—11月，本研究选择该时间段的气象数据进行分析。综合考虑天气条件尤其是降雨量要素，将整个观测期分为前期(5—7月)和后期(8—11月)2个阶段。所用气象资料均取自观测研究站逐日气象数据(共428 d，无数据缺失)，主要气象参数包括空气温度、风速、大气压强、相对湿度、太阳总辐射及日照时数等。

1.2 计算方法

(1)Penman-Monteith方法[1]

(1)

式中：ET0为参考作物蒸散量/(mm·d-1)；Rn为作物表面净辐射/(MJ·m-2·d-1)；G为土壤热通量/(MJ·m-2·d-1)；T为日平均气温/℃；U2为距离地面2 m高处的风速/(m·s-1)；es为饱和水汽压/kPa；ea为实际水汽压/kPa；Δ为温度-饱和水汽压关系曲线在温度t处的切线斜率/(kPa·℃-1)；γ为湿度计常数，γ=0.066，单位为kPa·℃-1。

(2)Hargreaves方法[19]

ET0=0.002 3Ra(t+17.8)(tmax-tmin)0.5

(2)

式中：Ra为太阳总辐射/(MJ·m-2·d-1)；T为日平均气温/℃；tmax、tmin为日最高气温、日最低气温/℃。

(3)Irmark-Allen方法[20]

ET0=0.489+0.289Rn+0.023T

(3)

式中：Rn为作物表面净辐射/(MJ·m-2·d-1)；t为日平均气温/℃。

(4)Priestley-Taylor方法[21]

(4)

式中：λ为水汽化潜热/(MJ·kg-1)；Δ为温度-饱和水汽压关系曲线在温度t处的切线斜率/(kPa·℃-1)；γ为湿度计常数，γ=0.066，单位为kPa·℃-1；Rn为作物表面净辐射/(MJ·m-2·d-1)；G为土壤热通量/(MJ·m-2·d-1)。

(5)Mc Clound方法[22]

ET0=0.254×1.071.18T

(5)

式中：T为日平均气温/℃。

(6)Penman1963方法[23]

(6)

式中：Δ为温度-饱和水汽压关系曲线在温度T处的切线斜率/(kPa·℃-1)；γ为湿度计常数，γ=0.066，单位为kPa·℃-1；Rn为作物表面净辐射为(MJ·m-2·d-1)；G为土壤热通量/(MJ·m-2·d-1)；aw、bw为风函数系数，aw=1，bw=0.537；U2为距离地面2 m高处的风速/(m·s-1)；es为饱和水汽压/kPa；ea为实际水汽压/kPa。

1.3 评价指标

本研究以PM方法的计算结果为标准，对其他5种方法的计算结果进行评估，分析其精度。评价指标包括平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)、一致性指数(d)，MAE、RMSE越接近于0，d越接近于1，则该方法和PM方法的误差越小、一致性越好、计算精度越高，其计算方法如下[10]：

(7)

(8)

(9)

式中：Pi为其他方法计算的ET0值/(mm·d-1)；Oi为PM方法计算的ET0值/(mm·d-1);O为PM方法所计算的ET0平均值/(mm·d-1)；n为样本数。

2 结果与分析

2.1 不同计算方法的ET0变化规律比较

根据2019年和2020年5—11月的逐日气象数据，分别计算得到6种方法的日ET0值和月ET0值(图1、图2)。从图1中可以发现，5种方法计算的ET0变化趋势与PM方法基本一致，Hargreaves方法计算的ET0显著高于其他方法。线性回归分析变化斜率显示ET0呈逐渐下降趋势，均表现为观测前期(5—7月)ET0值较高，后期(8—11月)ET0值逐渐下降。主要原因在于该地区春旱较为明显，观测前期降雨稀少。以2019年为例，5—7月降雨量仅有93.5 mm，占总降雨量的19.2%，使得空气温度高，相对湿度小，晴天较多，净辐射强，植物蒸腾和土壤蒸发强烈，导致ET0较高。8—10月降雨较为集中，降雨量为392.30 mm，尤其是8月份高达235.90 mm，连续的阴雨天气使得相对湿度增加，空气温度和净辐射较前一阶段分别降低了29.5%和16.7%，导致ET0逐渐下降。基于PM方法计算的2019年和2020年ET0总值分别为678.96和539.83 mm，平均值为609.40 mm(表1)，日ET0最大值出现在5、6月份(图2)，日均值4.70 mm。

各方法的计算结果与PM方法之间差异较大(表1)，5种计算方法结果大小为：Hargreaves法>Penman1963法>Irmark-Allen法>Mc Clound法>Priestley-Taylor法，其中Hargreaves法、Irmark-Allen法和Penman1963法大于PM方法，Mc Clound法与Priestley-Taylor法小于PM方法。与PM法最接近的是Irmark-Allen法(784.81 mm)，其次是Penman1963法(929.80 mm)，误差最大的则是Hargreaves法(2 223.08 mm)。

2.2 不同计算方法的相关性分析

以PM方法的计算结果为标准，将其他5种方法的计算结果分别与PM方法进行相关性分析(图3)。从图3中可以发现，2019年和2020年各方法与PM方法间都具有极显著相关性(P<0.01)。其中Penman1963方法与PM方法的相关性最强，决定系数R2最大，2019年和2020年分别为0.98和0.99，说明在不考虑偏离程度的情况下，Penman 1963方法与PM方法的相关性最好。其余4种方法与PM方法间的相关性较强，其中Hargreaves方法、Priestley-Taylor方法和Irmark-Allen方法的R2分别为0.63和0.71、0.56和0.61、0.52和0.62，Mc Clound方法的R2最小，仅为0.49和0.45。

2.3 不同计算方法的误差比较

为进一步评价各计算方法与PM方法之间的差异，采用MAE、RMSE和d等评价指标对5种方法计算的参考作物蒸散量ET0值与PM方法进行误差分析(表2)。由表2可知，Mc Clound方法、Penman 1963方法和Irmark-Allen方法的MAE较小，分别为1.44、1.50和1.51 mm·d-1，其次为Priestley-Taylor方法，MAE为1.87 mm·d-1，Hargreaves方法的MAE最大，为7.56 mm·d-1。Irmark-Allen方法和Penman1963方法的RMSE最小，分别为1.77和1.79 mm·d-1，其次为Mc Clound方法和Priestley-Taylor方法，RMSE分别为2.13和2.56 mm·d-1，Hargreaves方法的RMSE最大，为8.25 mm·d-1。Penman1963方法和Irmark-Allen方法的一致性指数d最高，分别为89.03%和73.48%，其次为Mc Clound方法和Priestley-Taylor方法，两者分别为56.04%和54.00%，Hargreaves方法的一致性指数最小，为38.54%。综合2 a观测期内各方法的评价指标来看，Penman1963方法和Irmark-Allen方法与PM方法间的误差最小，其次为Mc Clound方法和Priestley-Taylor方法，Hargreaves方法的误差最大。

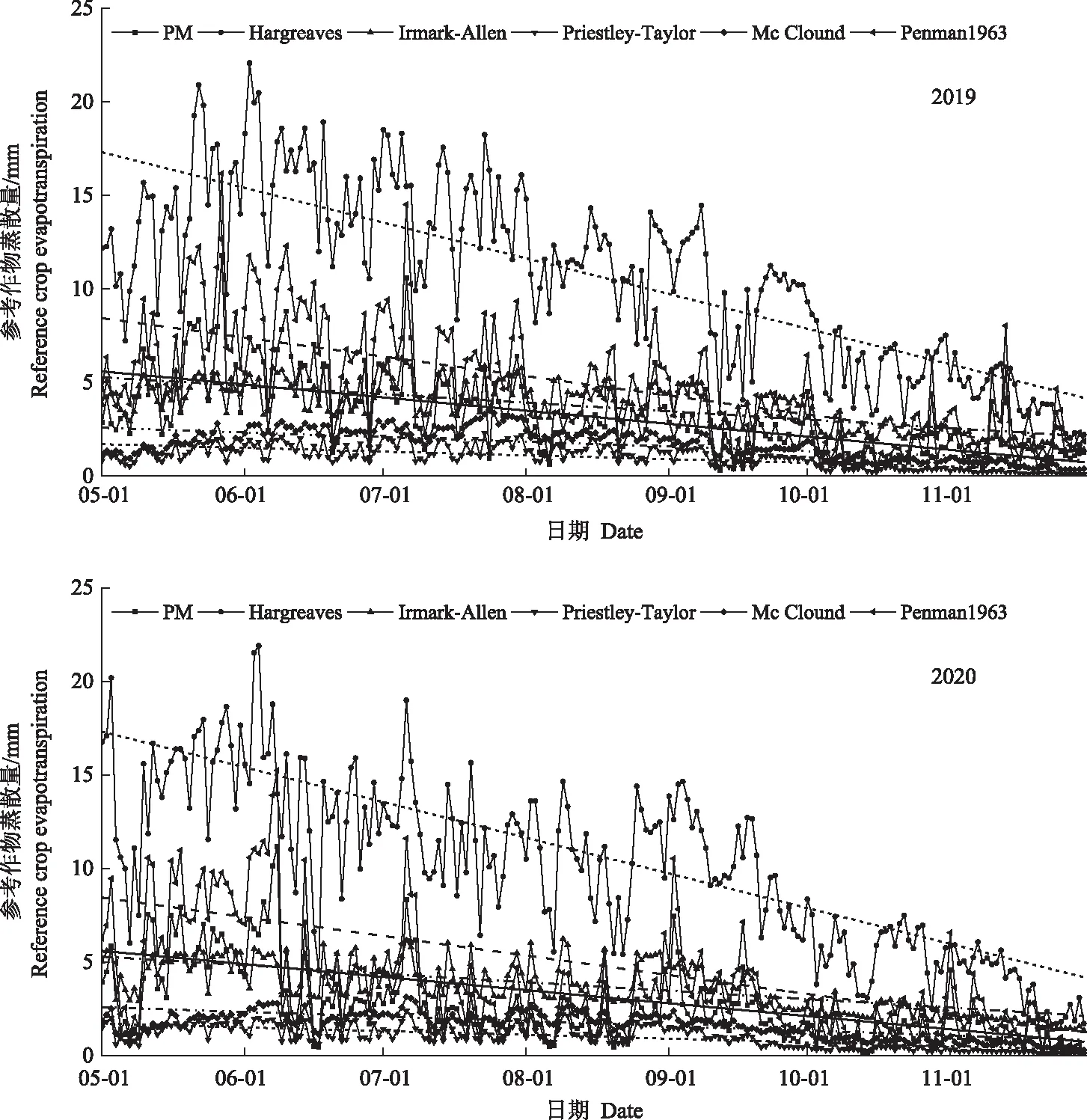
图1 不同方法计算的参考作物蒸散量日变化(2019—2020)Fig.1 Daily variation of reference crop evapotranspiration calculated by different methods (2019—2020)

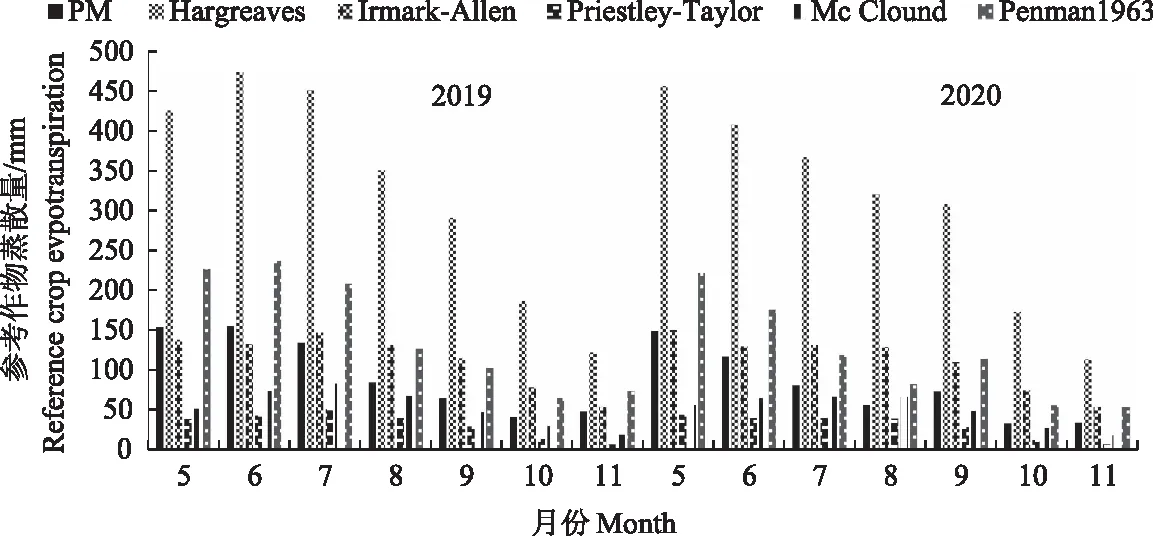
图2 不同方法计算的参考作物蒸散量月变化(2019—2020)

表1 不同计算方法月ET0比较(2019—2020年)Table 1 Comparison of monthly ET0 based on different calculation methods (2019—2020) mm

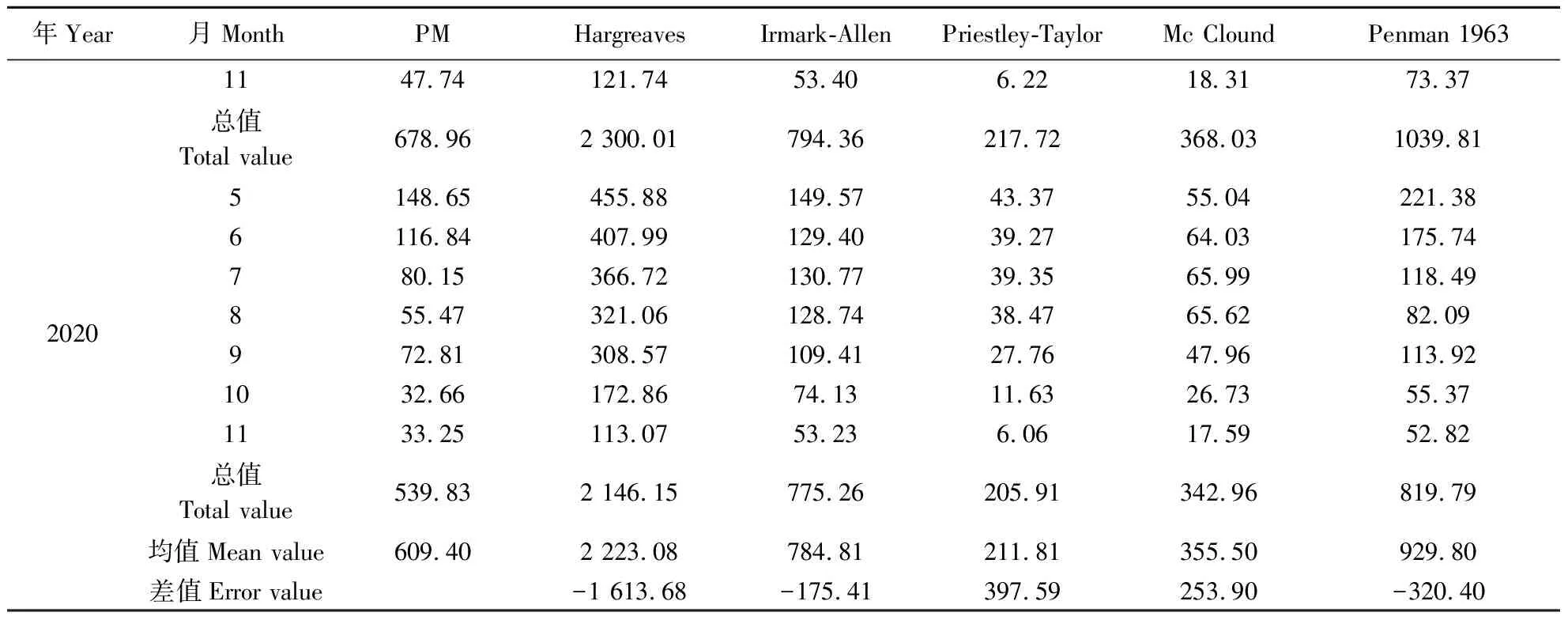
续表 Continuing table

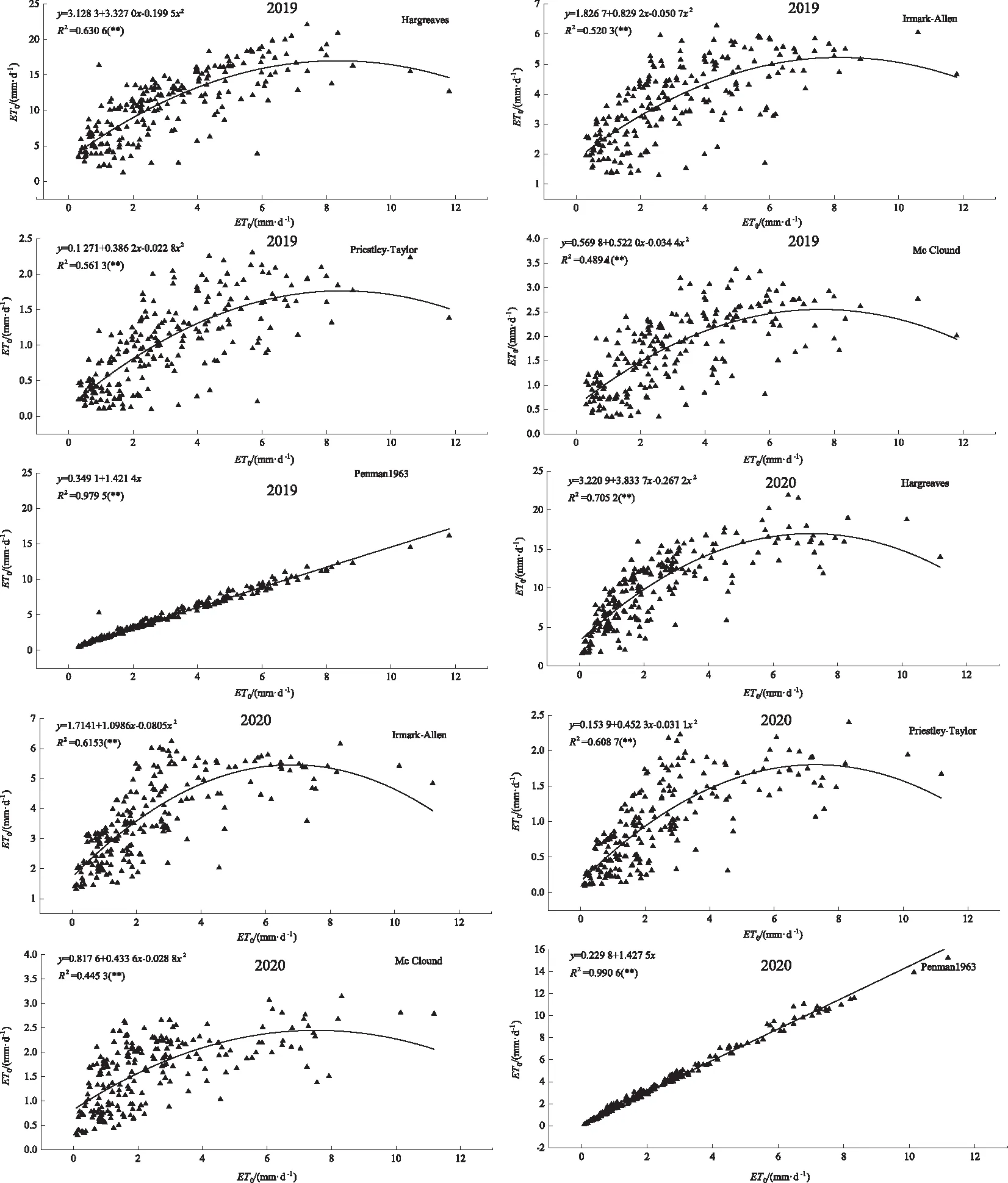
图3 不同计算方法与PM方法的相关性分析

表2 5种方法与PM方法的误差分析(n=428)

3 结论与讨论

本研究以Penman-Monteith方法的计算结果为标准，比较了5种ET0计算方法在华北土石山区的适用性，以便在缺少气象数据条件下找到一种有效的方法替代PM方法。5种方法与PM方法计算的标准值变化趋势基本一致。Irmark-Allen方法与PM方法的计算结果最接近，Hargreaves方法和Penman1963方法的计算结果大于标准值，而Priestley-Taylor方法和Mc Clound方法的计算结果则小于标准值。各方法与PM方法间均具有极显著相关性关系。Penman1963方法与PM方法的相关性最强，Hargreaves方法、Priestley-Taylor方法和Irmark-Allen方法次之，Mc Clound方法最小。Penman 1963方法和Irmark-Allen方法与PM方法间的误差最小，Hargreaves方法最大。综合来看，Irmark-Allen方法更适合代替PM方法来计算华北土石山区的ET0。

本研究发现，Irmark-Allen方法的计算结果与PM方法最为接近，且误差较小，与李银坤等[24]的结论一致。主要原因在于研究区光照充足，2019年和2020年太阳净辐射分别为1 999.84和1 946.43 MJ·m-2，ET0受太阳净辐射和温度影响较大，该方法综合考虑了太阳净辐射和温度的影响，因此计算精度较高。但李晨等[3]、赵璐等[25]则发现Irmark-Allen方法计算误差较大，这可能是因为该方法起源于湿润地区，忽略了相对湿度的影响，而相对湿度是ET0的主要影响因子。二者的研究区域均位于四川，导致该方法计算的误差较大，也说明该方法在四川的适用性较差。Priestley-Taylor方法与Irmark-Allen方法同属于辐射法，但其计算结果小于PM方法，与PM方法间的误差较大。本研究与GAO等[10]、魏光辉等[11]、汤鹏程等[26]、CELESIN等[27]、SHAFIEIYOUN等[28]的研究结果类似，主要原因在于Priestley-Taylor方法默认研究区域是湿润的，忽略了相对湿度对ET0的影响，而华北土石山区因降雨分配不均匀导致相对湿度变化明显，表现为雨季相对湿度大，非雨季相对湿度小，2019年和2020年相对湿度最大值均出现在8月份，分别为74.84%和86.10%，最小值均出现在5月份，分别为44.29%和50.81%，相对湿度的巨大变化使得Priestley-Taylor方法低估干旱地区ET0。而朱潇枭等[29]、LU等[17]则发现Priestley-Taylor方法在海南省、美国东南部有较好的适用性，因为海南省和美国东南部地处热带、亚热带湿润性气候带，降雨充沛，相对湿度变化较小，太阳辐射在湿润气候条件下估算ET0时起了重要的作用[30]，因此Priestley-Taylor方法计算结果误差较小。

Hargreaves方法属于温度法，与PM方法间的相关性虽较好，但计算结果远大于PM方法，误差也最高。徐冰等[15]、XU等[31]、FENG等[32]的研究结果也证实了这一结论。主要原因在于Hargreaves方法所需参数除了太阳辐射外，还需要平均气温、最高气温和最低气温，温差对其计算精度影响较大。试验地2019年和2020年平均温差分别为11.3和10.5 ℃，其中2019年5月22日、6月2日和2020年5月3日、6月3日温差分别高达24.0、24.0、23.7和23.8 ℃，温差越大，导致Hargreaves方法计算的ET0越大，与PM方法结算结果误差更大。而李晨等[3]在四川不同区域研究发现Hargreaves方法、Pristley-Taylor方法与PM计算方法间的误差较小，适用性好。可能是因为Hargreaves方法采用的温度参数容易受到风速、天气和云层厚度的影响，而四川省属于亚热带季风性湿润气候，受常年云层遮挡的影响，太阳辐射小，气温日较差小，因此Hargreaves方法在当地的适用性较好。而同属于温度法的Mc Clound方法的计算结果小于PM方法，与PM方法间的相关性也最低，与LIU等[4]、刘松林等[33]研究结果一致。主要原因在于Mc Clound方法只考虑了平均气温在计算ET0中的影响，忽略了太阳净辐射对ET0的贡献，研究区光照充足，不考虑太阳净辐射导致该方法的计算结果误差较大。Penman1963方法的计算结果与PM方法接近，误差也最小，与LIU等[4]、曹金峰等[34]的结论一致。这主要是因为Penman1963方法和PM方法均属综合法，综合法以能量平衡和水汽扩散理论为基础，综合考虑了影响ET0的关键因子太阳辐射和水汽压亏缺[4,30]，因此，其适用性和精度高于辐射法和温度法。