基于多DEA-Gini的纺织业碳排放效率时空分异研究

马玉超，张永林

基于多DEA-Gini的纺织业碳排放效率时空分异研究

马玉超，张永林

（武汉纺织大学 管理学院，湖北 武汉 430200）

基于2010年到2019年我国30个省（市，自治区）纺织业的面板数据，采用多种DEA模型并结合Gini准则对其碳排放效率进行测度，并利用全局趋势分析法、探索性空间数据分析法和标准差椭圆技术揭示其时空分异特征。研究发现：观察期内，我国各省份纺织业碳排放效率差距明显，存在集聚趋势；纺织业碳排放效率在东西和南北方向均呈现倒“U”型趋势，且东西（南北）方向上的差距有所缩小（扩大）；纺织业碳排放效率自2017年开始表现出显著的正向空间自相关性；纺织业碳排放效率区位分布由偏东北—偏西南转变为偏东南—偏西北，分布重心向南移动。最后，根据研究发现提出若干政策建议。

纺织业；Gini准则；碳排放效率；时空分异

我国在“十三五”期间已经基本实现了从纺织大国到纺织强国的转变，我国纺织业在全球价值链中的位置稳步提升，整体竞争力进一步增强。有关资料显示，我国在2020年的纺织纤维加工总量占世界纤维加工总量的一半以上，化纤产量更是达到了70%以上的占比，我国纺织品服装出口额稳居世界首位[1]。随着全球气候治理形势的日益紧迫，我国提出了“争取二氧化碳排放量在2030年前达到峰值，在2060年前实现碳中和”的目标愿景，这对高能耗、高污染的纺织业形成了刚性要求。因此，在“十四五”期间，纺织业作为国民经济和社会发展的支柱产业，迫切需要实现高质量发展。纺织业碳排放效率的测算是实现我国纺织业高质量发展的重要决策依据，中国地大物博，由于各地区资源禀赋不同，各地区纺织业发展水平也不尽相同，纺织业碳排放效率也可能存在时空分异现象。于是对我国纺织业碳排放效率进行科学测算，探索其时空分异，对于促进我国纺织业高质量发展与我国“双碳”目标的实现有着重大意义。

1 文献回顾

关于碳排放效率，国内外相关研究已取得不少成果。碳排放效率可以分为单要素碳排放效率和全要素碳排放效率。早期研究主要以单要素碳排放效率为主，例如以碳指数[1]、碳排放强度[3]、能源强度[4]等指标来衡量碳排放效率，仅考虑了碳排放量和GDP、人口等单个变量的关系。而近年来学者们开始关注于全要素碳排放效率，将经济、能源和环境纳入测算指标，使得碳排放效率的测算指标更为全面。如今关于碳排放效率测度的对象，已有学者将国家或者地区作为对象测算其碳排放效率，同时也有众多学者针对不同产业开展了丰富的研究，例如工业[5]、交通运输业[6, 7]、制造业[8]、物流业[9]、农业[10]等。然而，目前学界对纺织业的关注度相对较低，吕明元等测算了我国纺织业的生态效率并对其结构性因素进行分析[11]。Zhao和Lin测算了我国纺织业在碳排放约束下的能源效率[12]。Lin和Bai测算了我国各省的纺织业能源绩效，发现在不同的时空尺度上，中国三大地理区域的动态能源效率呈上升趋势[13]。Gai等认为纺织业子行业对环境造成的影响存在差异，于是将重点放在棉化纤纺织行业、非棉纺织行业和印染行业，对三个子行业的生态效率进行了测度，结果发现三个子行业之间的差异较大[14]。从研究尺度来看，已有关于碳排放效率测算的研究主要基于国家、区域、省域和县域层面。从测算方法来看，如今的主流方法主要有三类。第一类是通过构建绿色技术创新评价指标体系，然后采用熵值法等客观评价方法测算碳排放效率[15, 16]，这类方法具有简单易懂且能够避免人为因素导致结果出现偏差等优点，但是忽略了指标本身的重要程度。第二类方法是采用随机前沿分析法（SFA）测算碳排放效率[17, 18]，SFA是参数方法的典型代表，其优点是能够考虑随机因素对产出的影响，其缺点是需要事先对生产前沿的具体形式进行确定，且模型中只能有一个产出指标。第三类方法则是数据包络分析法（DEA），其为非参数方法的代表，这类方法可以有效解决SFA模型的局限之处，因此得到广泛应用，且发展出了各种形式，例如BCC[19]、超效率DEA[20]、SBM[21]、EBM[22]、MinDS[23]、DDF等模型[24]。

空间分异最初来源于地理学，是指某一属性在不同地理区域之间存在的差异。本文增加时间维度的考量，将纺织业碳排放效率时空分异界定为“纺织业碳排放效率在地理区域之间存在的差异，以及差异在时间维度上的变化规律”。关于碳排放效率的空间分异，已有学者从不同角度开展了研究，但是目前以纺织业为对象的研究却凤毛麟角。王兴民等基于198个地级市数据，发现中国城市层面的CO2排放存在明显的空间分异[25]。牛亚文等基于县域数据测算了长株潭地区的土地利用碳排放并分析其空间分异现象[26]。高新才和韩雪研究了黄河流域碳排放的空间分异，发现黄河流域碳排放效率呈现出较强的空间相关性且有加强趋势，碳排放分布存在较强的转移惰性[27]。韩传峰等则采用多种空间数据分析方法对长三角地区城市层面的碳排放空间分异进行分析[28]。

综上所述，可以看出现有关于碳排放效率测算及其空间分异的研究已经取得了丰硕的研究成果，但仍然存在一些不足之处：首先，现有关于碳排放效率测算的研究对纺织业的关注较少，而纺织业是我国经济与社会发展的支柱产业，同时也是我国开展国际合作和融合发展的优势产业，其对于民生和美化生活具有重要作用；其次，在碳排放效率测算方法上，现有绝大多数研究多采用单一DEA模型，由于每个测算模型都具有从自身角度出发的有价值的信息，采用单一模型可能会导致结果出现偏误或者不可比的情况；最后，对于纺织业碳排放效率的时空分异特征，目前还几乎没有学者进行探讨。鉴于此，本文为了丰富纺织业碳排放效率的相关研究，从以下方面对现有研究进行拓展：一是参考相关研究，采用多DEA-Gini方法对纺织业碳排放效率进行测算，避免使用单一模型存在的风险；二是基于ArcGIS平台，采用多种空间分析方法实证考察我国纺织业碳排放效率的时空分异特征。从碳排放效率视角对纺织业进行研究，可以为政府部门制定有针对性的纺织业低碳发展战略提供理论和实证依据，进而有利于纺织业的转型升级和高质量发展。

2 研究设计

2.1 多DEA-Gini准则模型

本文采用了多种DEA模型对2010年到2019年中国30个省、直辖市和自治区（不含西藏和港澳台）的纺织业碳排放效率进行了测度，然后采用数据挖掘分类回归决策树理论中的Gini准则来对各DEA模型赋予权重，最终计算出结合多种DEA模型所得结果的综合值[29]，以避免重要信息被忽略和效率结果不可比的情况。本文首先基于规模报酬不变和可变假设，然后考虑到DEA结果可能会出现很多“1”从而导致无法对决策单元进行进一步的比较，于是最终选择了规模报酬不变假设下的SBM模型和超效率SBM模型、规模报酬可变假设下的SBM模型和超效率SBM模型。根据这四种不同的DEA模型测算出的不同结果，通过Gini准则，得到综合效率值。

2.1.1 标准效率和超效率SBM模型

本文采用的标准效率和超效率SBM模型的具体形式如下所示。

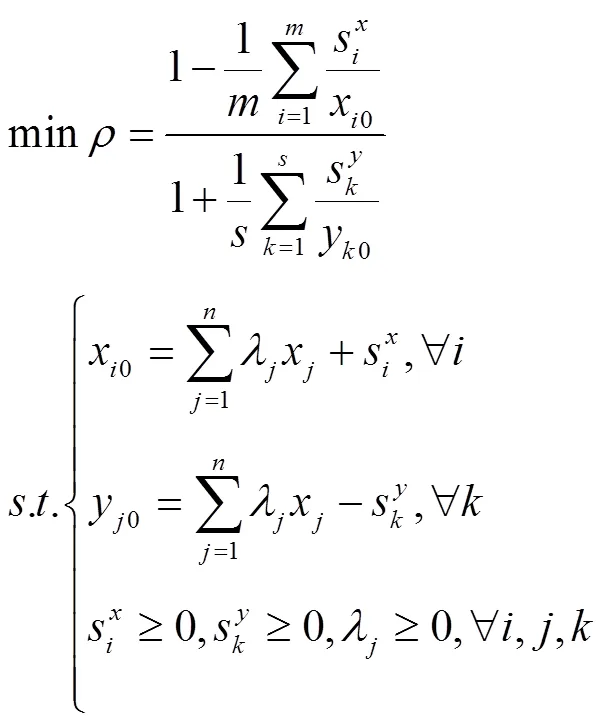
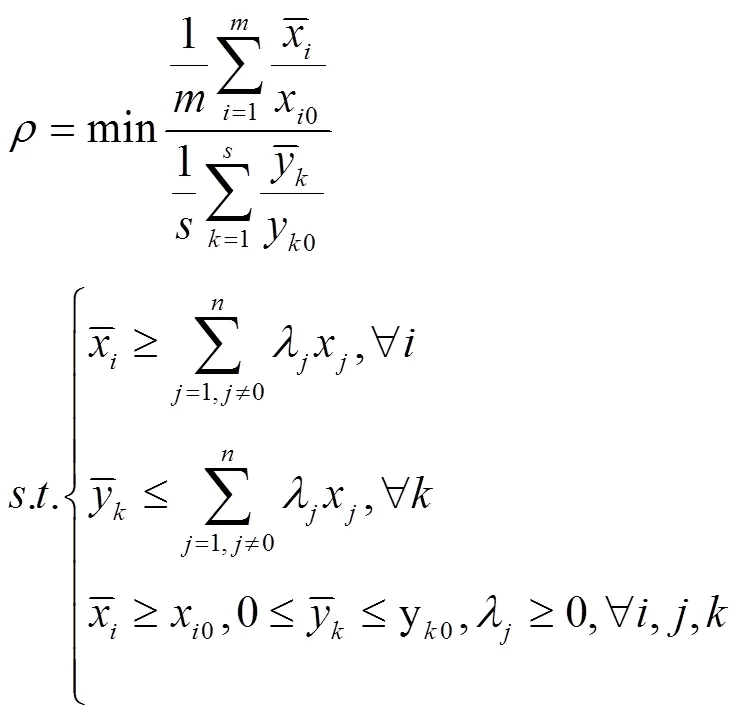
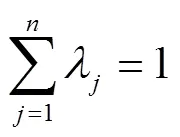
2.1.2 Gini准则

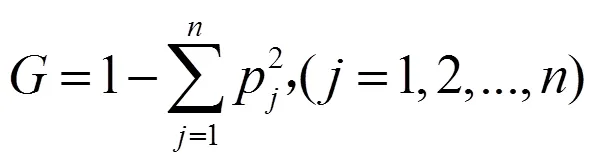
2.1.3 多DEA-Gini准则方法步骤

参考薛晖等[29]的研究，本文采用的多DEA- Gini准则方法步骤如下。

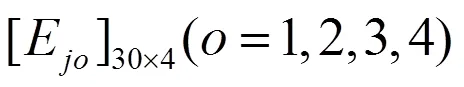
2.2 全局趋势分析法

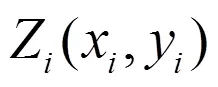
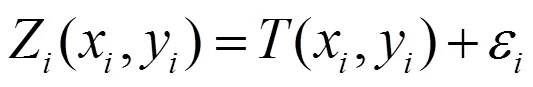
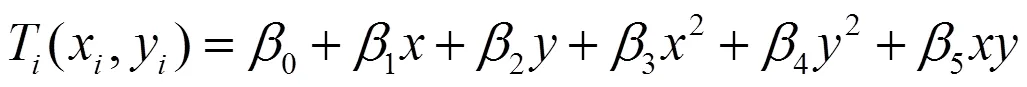
2.3 探索性空间数据分析法

探索性空间数据分析（ESDA）是一种具有识别功能的空间数据分析方法，主要用于探测某些变量的空间相关性和集聚性。目前，该方法已经在多个领域得到了广泛应用，最为常见的有全局莫兰指数和局部莫兰指数（LISA），在本文中可以检验纺织业碳排放效率在整体上的空间自相关性和局部上的集聚性。全局莫兰指数大于0则表示空间正相关，值越接近1表示具有相似属性的地区越倾向于聚集在一起（即高值与高值邻接，低值与低值邻接）；全局莫兰指数小于0表示空间负相关，值越接近-1表示具有相异属性的地区越倾向于聚集在一起（即高值与低值邻接，低值与高值邻接）；全局莫兰指数接近0时，则表示该属性是随机分布的，不存在空间相关性。与全局莫兰指数相似，局部莫兰指数（LISA）为正，则表示一个高值被高值所包围（高—高），或者是一个低值被低值所包围（低—低）；若指数为负，则表示一个低值被高值所包围（低—高），或者是一个高值被低值所包围（高—低）[31]。两种指数的计算方法见式5和6。

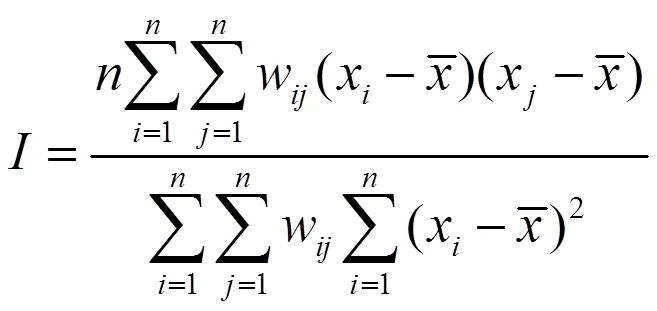
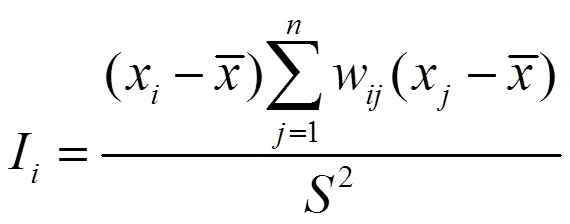
2.4 标准差椭圆

标准差椭圆是一种衡量地理要素空间分布特征的统计技术，但该方法也在诸多其他领域得到广泛应用。在本文中，采用标准差椭圆来考察我国纺织业碳排放效率的空间集聚和区位特征。标准差椭圆分析中的重要参数包括分布重心、椭圆长短半轴和方位角等，具体计算公式参考刘华军等[32]。

2.5 指标设定与数据来源

根据柯布-道格拉斯生产函数的思想，并结合本文的特点，在文中主要有资本、劳动力和能源三种投入变量。其中资本投入由各省份纺织业固定资产投资额表示，劳动力投入由各省份纺织业就业人数表示，由于能源消耗量和碳排放量具有线性关系，如今国家提倡节能减排，碳排放量越小越好，符合作为DEA投入指标的条件，因此在本文中用各省份纺织业二氧化碳排放量代替能源投入。产出变量采用各地区纺织业主营业务收入代表。

资本投入数据来源于2011年到2020年的《中国固定资产统计年鉴》和《中国纺织工业发展报告》，劳动力投入数据来源于2011年到2020年的《中国劳动统计年鉴》，碳排放量数据来源于中国碳核算数据库（CEADs）（https://www.ceads.net.cn/），与IPCC公布的碳排放数据相比，中国碳核算数据库基于表观能耗数据和更新之后的中国的碳排放因子，从而提供的数据更加准确[33]。产出数据来源于2011年到2020年的《中国工业统计年鉴》。

3 中国纺织业碳排放效率评价结果

多DEA-Gini准则方法计算出的各个模型的权重值如表1所示。在四种DEA模型中，基于规模报酬可变假设的超效率SBM模型的信息纯度最大，为0.0049，因此应该给予该模型较大的权重值；基于规模报酬可变假设的标准效率SBM模型的信息纯度最小，为0.0037，因此应该给予该模型较小的权重值。最终，基于规模报酬不变和可变假设的标准效率SBM模型、基于规模报酬不变和可变假设的超效率SBM模型的权重值分别为0.228、0.223、0.254、0.295。将四种DEA模型的结果根据权重值加总所得综合效率结果如表2所示。受限于篇幅，本文只选取2010、2013、2016、2019年的效率结果进行汇报。

多DEA-Gini方法测算结果显示，在观察期内我国纺织业碳排放效率均值有所上升，但上升幅度较小，我国绝大多数省份的纺织业碳排放效率小于1，具有较大的提升空间。为了将效率测度结果进行直观展示，本文借助ArcGIS10.5软件对我国30个省份的纺织业碳排放效率进行可视化展示。具体方法为，将我国30个省份的纺织业碳排放效率数据导入ArcGIS10.5软件，采用自然断点法（Natural Breaks）将各省份按照纺织业碳排放效率高低分为5个等级，分别为高、较高、中等、较低和低效率，由此得到我国纺织业碳排放效率的空间分布地图（图1）。从图1中可以发现，高效率水平地区有青海、宁夏、海南，效率均值较高的地区有北京、内蒙古、江苏、安徽、河南、湖北、江西、贵州等地；低效率水平地区有黑龙江、吉林、山西、广西和云南，效率均值较低的地区有辽宁、天津、广东、重庆、四川、甘肃、新疆等地；其余省份效率水平居中。从空间分布格局的演变来看，随着时间的推移，纺织业碳排放效率呈现出一定的聚集趋势，具体表现为效率较高地区发生聚集（主要分布在东南沿海和中部地区），效率较低的地区发生聚集（主要分布在东北地区，部分北方地区和西南地区）。

表1 各模型权重值

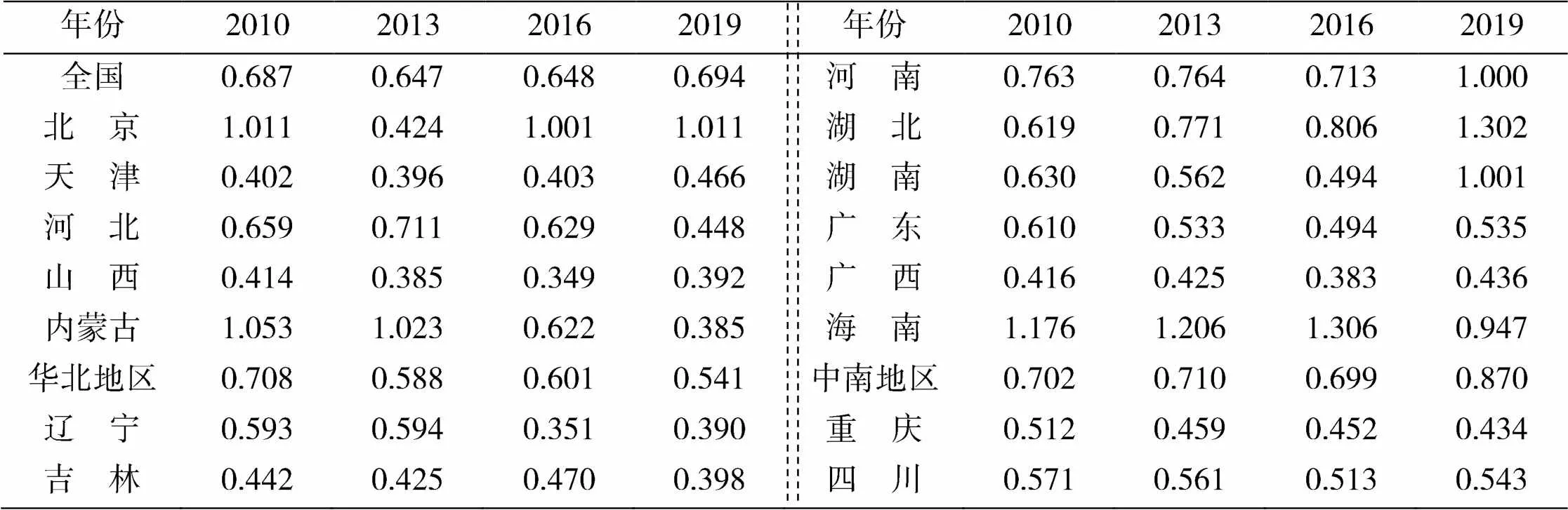
表2 纺织业碳排放效率结果

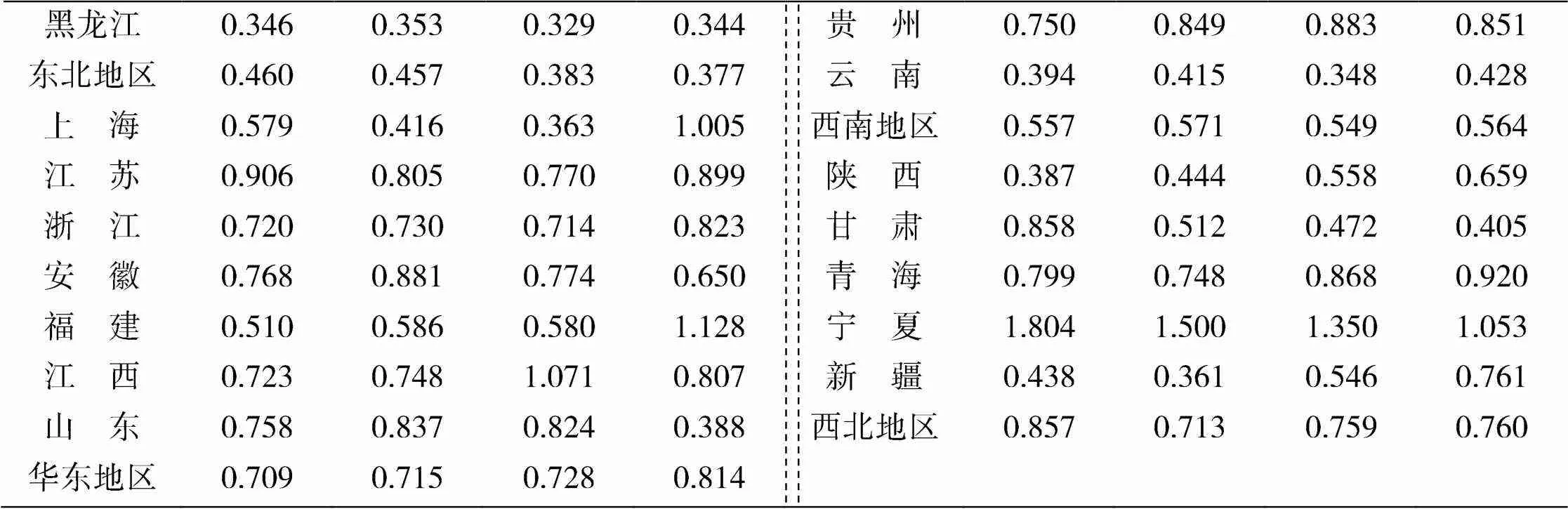
续表2

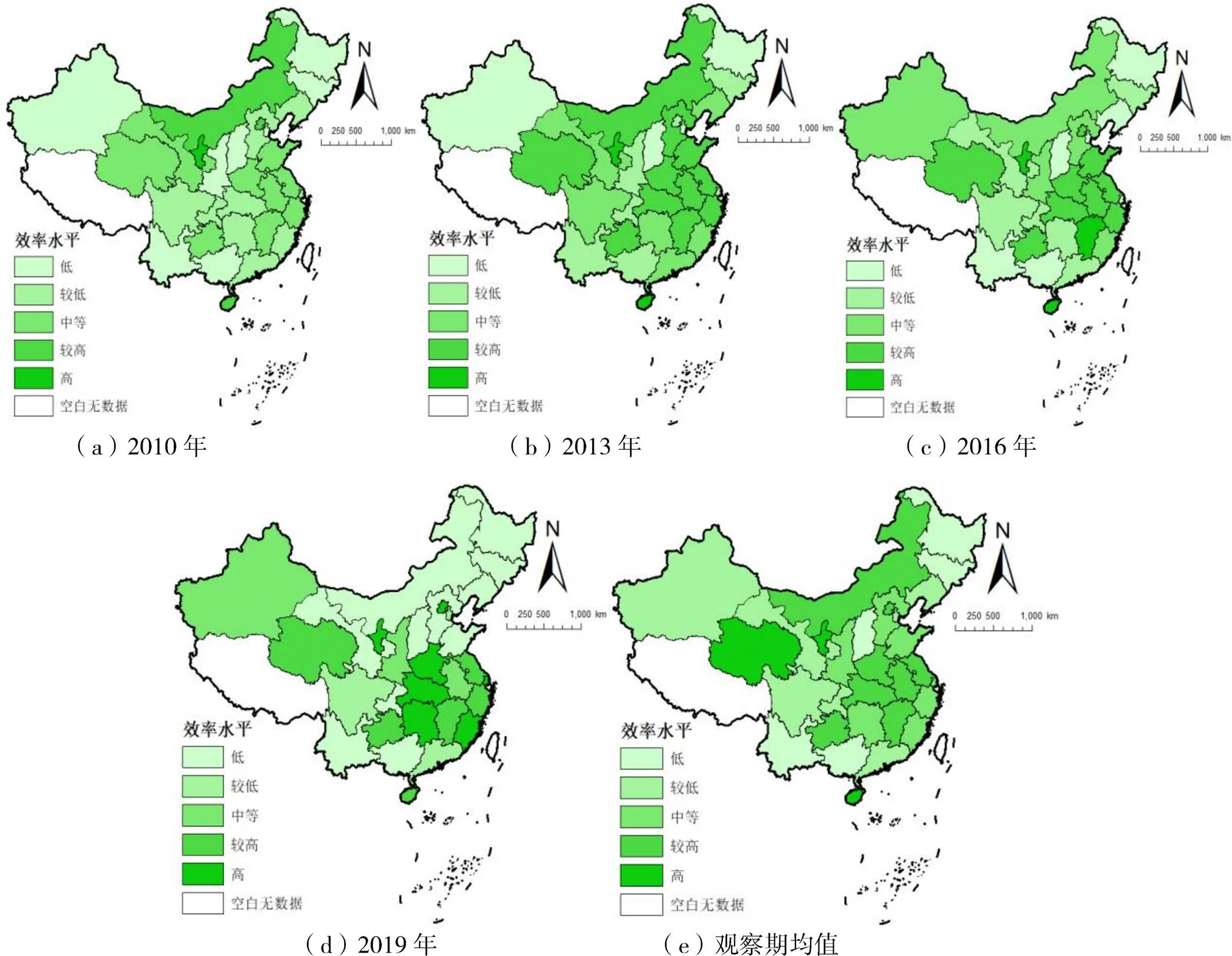
图1 中国纺织业碳排放效率空间分布

注：该图基于国家自然资源部标准地图（审图号：GS(2019)1822号）绘制，底图无修改。

4 中国纺织业碳排放效率时空分异分析

4.1 全局趋势分析

以正东和正北方向作为X轴和Y轴，以纺织业碳排放效率作为 Z轴，以此直观显示2010到2019年我国纺织业碳排放效率的空间分布趋势（图2）。从趋势线图2中可以发现，我国纺织业碳排放效率在东西方向和南北方向上均呈现出倒“U”型趋势，这表明我国纺织业碳排放效率存在明显的空间非均衡状态，总体呈现出中心高，周围低的空间分布趋势。随着时间的推移，效率空间分布趋势也发生了变化，图中趋势曲线的弧度越大，表明纺织业碳排放效率间的差异越大。从趋势曲线的弧度变化可以发现，在观察期内，东西方向的趋势曲线弧度有所减小，南北方向的趋势曲线弧度有所增大，两种方向上仍然保持着倒“U”型趋势，这表明我国纺织业碳排放效率在东西方向上的差距有减少的趋势，南北方向上的差距有扩大的趋势，且我国纺织业碳排放效率仍然显现中心高，四周低的空间分布趋势。

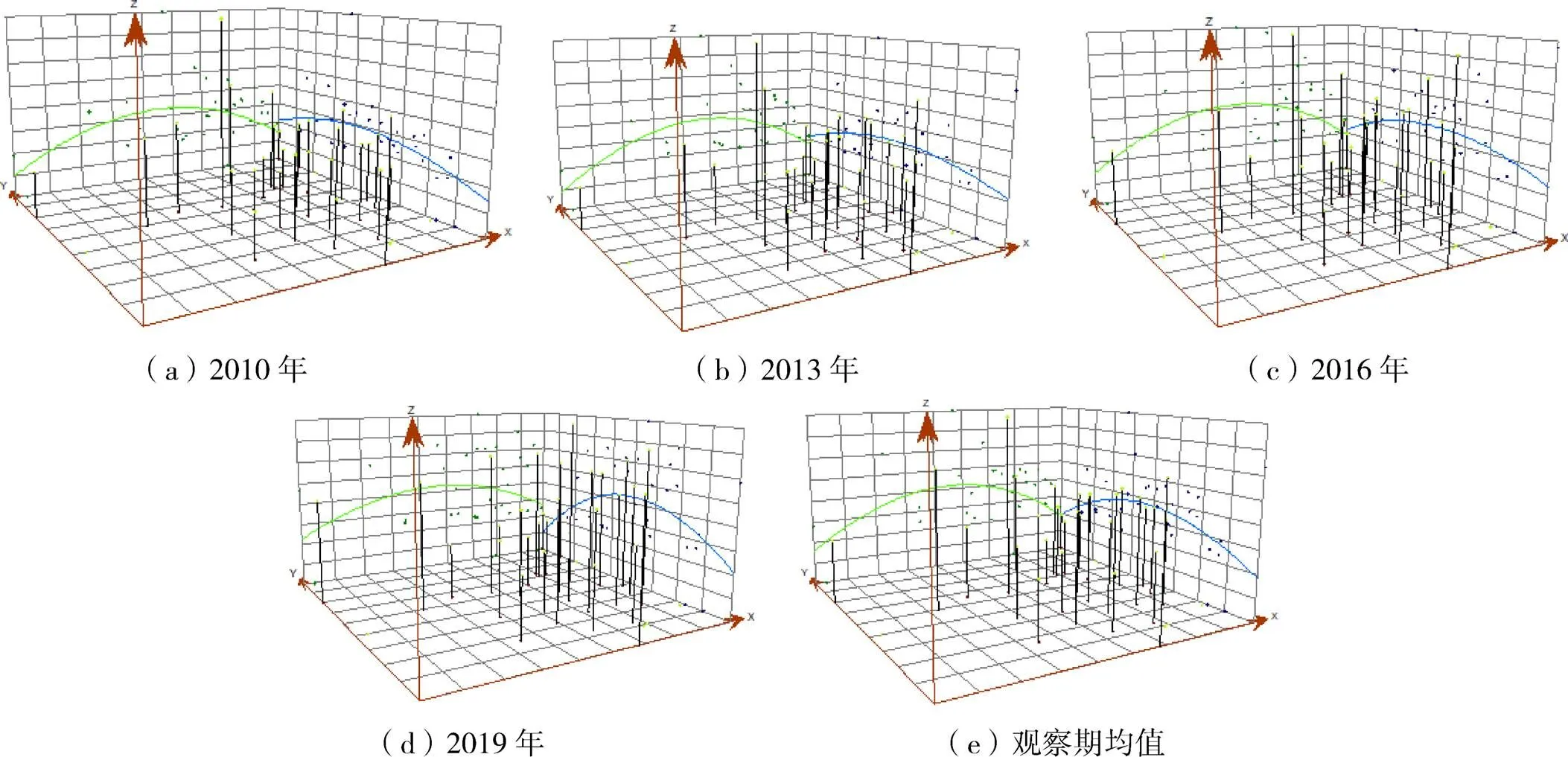
图2 中国纺织业碳排放效率空间趋势线

4.2 空间自相关性分析

全局空间自相关性检验结果见表3。可以发现，我国纺织业碳排放效率的全局莫兰指数在2010年到2016年期间为负，且未通过显著性水平检验，表明我国纺织业碳排放效率在此期间不存在显著的空间自相关性。然而，自2017年起，莫兰指数由负转正，且通过了显著性水平检验，表明我国纺织业碳排放效率开始表现出显著的正向空间自相关性，即高效率地区与高效率地区聚集，低效率地区与低效率地区聚集，这验证了前文通过直观观察所得出的结论。

表3 全局莫兰检验结果

全局莫兰指数检验无法反映局部地区的集聚情况，本文进一步对局部空间自相关性进行检验，结果采用LISA集聚地图形式展示，经过分别对2010年、2013年、2016年和2019年的纺织业碳排放效率局部空间自相关检验发现，2010年和2013年不存在显著的局部空间自相关性，2016年和2019年存在显著的局部空间自相关性。因此，限于篇幅，仅展示2016和2019年的LISA集聚地图，如图3所示。在2016年，只有安徽省位于高—高值集聚区，同时在5%的水平上显著；处于高—低集聚区的只有贵州省，且通过了5%的显著性水平检验。在2019年，江西省成为唯一位于高—高值集聚区的省份，在1%的水平上显著；内蒙古、黑龙江、吉林、辽宁等地属于低—低值集聚区，分别在5%、5%、1%、5%的水平上显著。

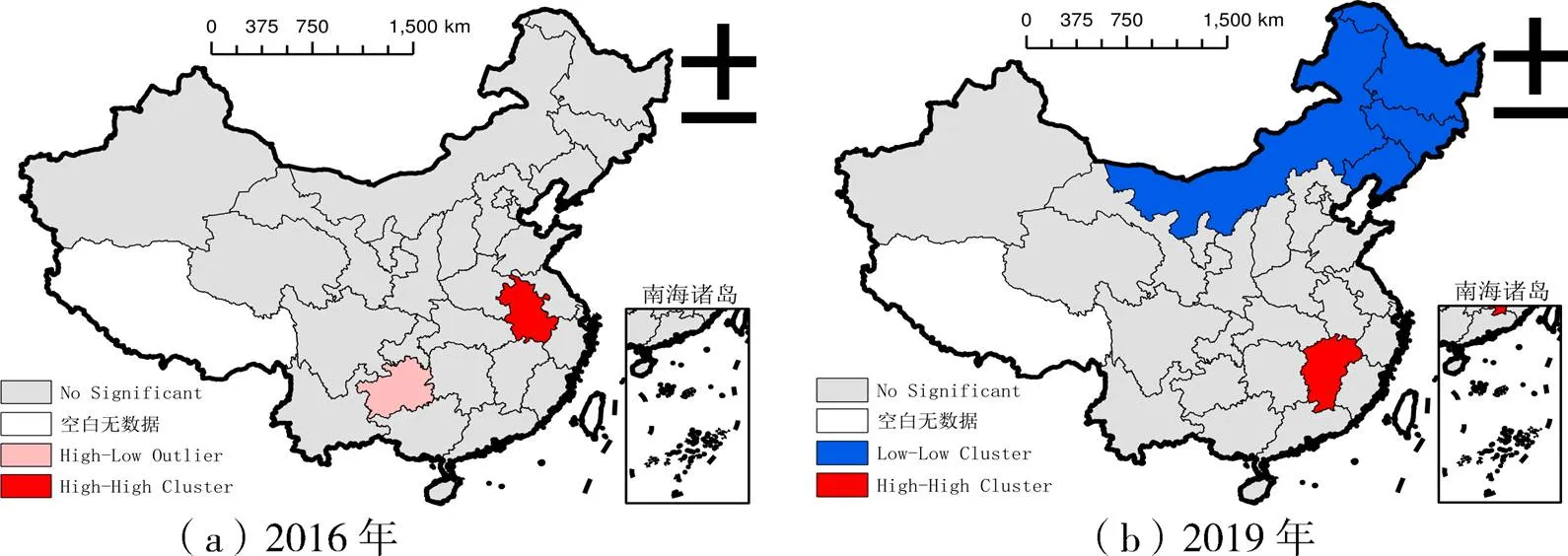
图3 中国纺织业碳排放效率LISA集聚图

注：该图基于国家自然资源部标准地图（审图号：GS(2019)1822号）绘制，底图无修改。

4.3 标准差椭圆分析

我国纺织业碳排放效率的标准差椭圆及重心转移情况如图4所示，相关参数见表4。从椭圆形状来看，2010年、2013年、2016年和2019年的平均形状指数分别为0.88、0.84、0.91、0.95，呈现出增加态势，形状接近于正圆，这说明向心力较弱，意味着集聚区内各省份的纺织业碳排放效率更加均衡。从方位角来看，纺织业碳排放效率的标准差椭圆在观察期内从偏东北—偏西南向偏东南—偏西北方向旋转了112.314度，表明纺织业碳排放效率的空间分布方向具有较大的偏移趋势。具体从长短半轴来看，长半轴在观察期内有所缩短，短半轴在观察期内有所延长，结合方位角可知起初我国纺织业碳排放效率在偏东北—偏西南方向上的空间集聚特征有所增加，在偏东南—偏西北方向上的空间集聚特征有所下降，随后在偏东南—偏西北方向上的空间集聚特征有所增加，在偏东北—偏西南方向的空间集聚特征有所下降。从标准差椭圆的面积来看，2019年与2010年纺织业碳排放效率的标准差椭圆面积之比为1.014，变化程度较小，这说明纺织业碳排放效率的空间聚集特征未发生明显变化。从椭圆重心位置来看，纺织业碳排放效率的分布重心均位于河南省境内，但重心位置存在转移趋势，2010年位于栾川县和嵩县边界处，2013年和2016年位于内乡县境内，2019年移动至邓州市境内。整体来看，重心东西移动范围小于南北移动范围，意味着我国纺织业碳排放效率空间分布重心更倾向于在南北方向发生转移。

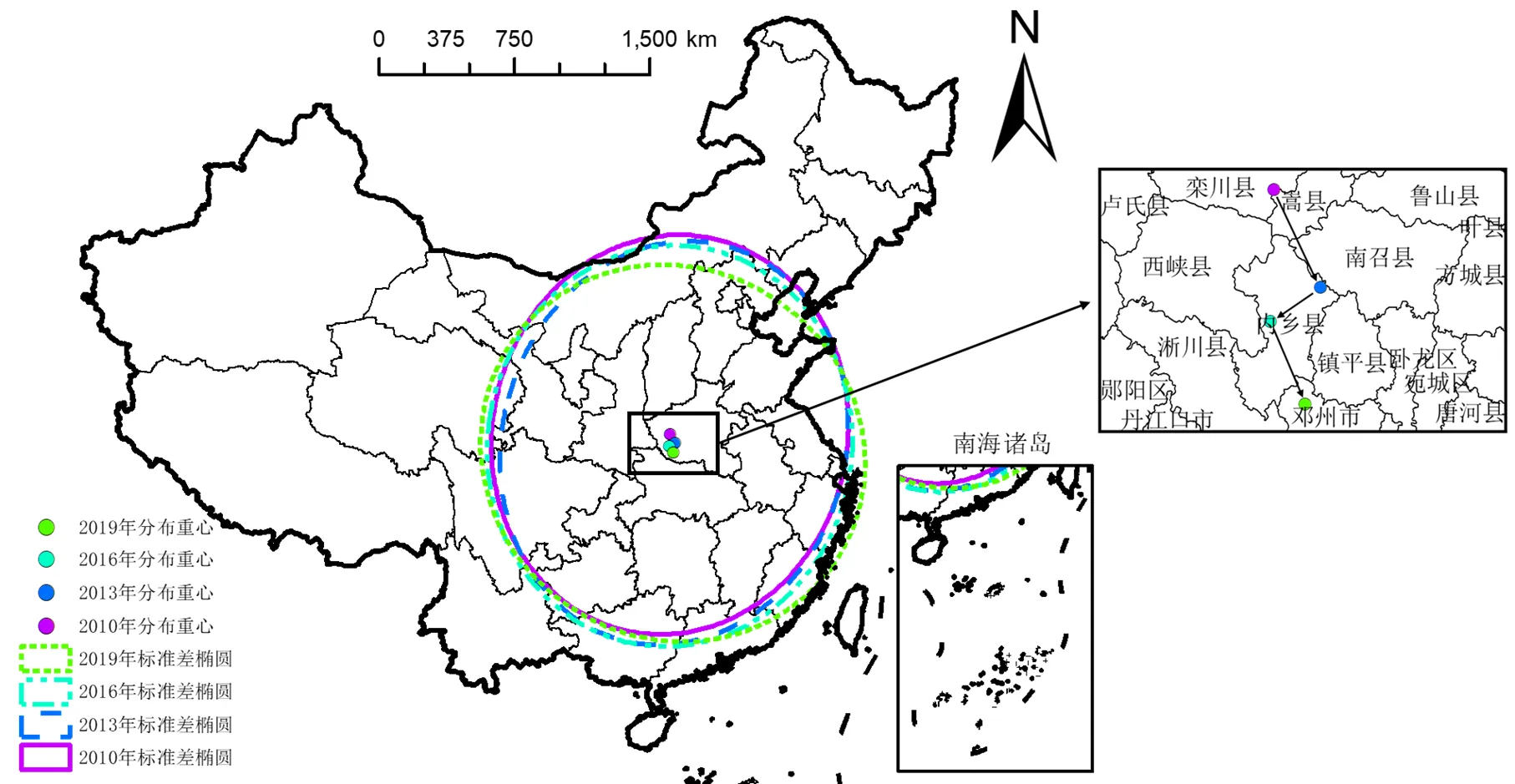
图4 中国纺织业碳排放效率标准差椭圆

注：该图基于国家自然资源部标准地图（审图号：GS(2019)1822号）绘制，底图无修改。

表4 中国纺织业碳排放效率标准差椭圆相关参数

5 结论与启示

5.1 研究结论

本文基于省级层面的纺织业数据，采用多种DEA模型并结合Gini准则对我国30个省（市，自治区）的纺织业碳排放效率进行了测算，并采用多种空间数据分析方法检验了纺织业碳排放效率的时空分异特征。本文主要有以下发现：（1）多DEA-Gini方法测算结果显示，2010年到2019年期间我国整体纺织业碳排放效率有小幅上升，绝大多数省份的效率值小于1，具有较大的提升空间。高水平地区有青海、宁夏、海南等地，低水平地区有黑龙江、吉林、山西、广西和云南等地，且随着时间推移，纺织业碳排放效率存在聚集趋势。（2）全局趋势分析结果显示，我国纺织业碳排放效率在东西和南北方向上均呈现出倒“U”型趋势，表明我国纺织业碳排放效率存在明显的空间非均衡状态，观察期内东西（南北）方向上的差距有缩小（扩大）的趋势。（3）空间自相关分析发现，我国纺织业碳排放效率空间自相关性在2010年到2016年期间不显著，但从2017年开始显著，局部空间自相关检验发现，2016年只有安徽省位于高—高值集聚区，贵州省处于高—低值集聚区，2019年江西省成为高—高值集聚区，内蒙古和东北三省为低—低值集聚区。（4）标准差椭圆分析发现，在观察期内，集聚区内各省份纺织业碳排放效率更加均衡，空间分布方向具有较大的偏移趋势，纺织业碳排放效率空间分布方向由偏东北—偏西南方向发散分布转向偏东南—偏西北方向发散分布，偏东南—偏西北方向的集聚程度有所增加，偏东北—偏西南方向的集聚程度有所下降，分布重心在观察期内表现出向南移动的趋势。

5.2 政策建议

本文基于研究发现和现实背景，提出以下政策建议：（1）加强低碳技术创新，推进节能低碳发展。纺织业高质量发展需要持续加强基础研究投入，实现关键技术突破，同时还要优化能源结构，鼓励企业使用清洁能源，提高二次能源消费比重，以达到碳排放量减少的目的。（2）提升区域协调发展水平。我国各省份纺织业发展相对孤立，高效率水平地区辐射带动能力不足，因此要加强地区之间的联系与合作，打破区域保护壁垒和要素流动藩篱，高效率水平地区和低效率水平地区要做到合理分工，实现优势互补。（3）因地制宜地制定发展模式。我国各地区之间纺织业碳排放效率具有明显差距，各省份应该充分考虑自身比较优势，探索不同的纺织业发展路径。比如，东部地区要借助自身良好的经济和技术基础，大力提高产业低碳水平，为其他地区树立产业标准；东北地区可以借助自身的工业基础，优化纺织业空间布局，挖掘地区低碳发展潜能。（4）推进高水平产业集聚发展。在京津冀城市群、长三角地区、粤港澳大湾区和长江经济带等战略区域落实行业发展重点，优先建设具有世界领先的创新能力、制造能力和可持续发展能力的纺织产业集群，发挥龙头企业跨区域布局的作用以带动中小纺织企业发展。

[1] 中国纺织工业联合会. 纺织工业“十四五”发展纲要[J]. 纺织科学研究, 2021, (07): 40-49.

[2] Mielnik O, Goldemberg J. The evolution of the “carbonization index” in developing countries[J]. Energy Policy, 1999, 27(5): 307-308.

[3] Sun J W. The decrease of CO2emission intensity is decarbonization at national and global levels[J]. Energy Policy, 2005, 33(8): 975-978.

[4] Ang B W. Is the energy intensity a less useful indicator than the carbon factor in the study of climate change?[J]. Energy Policy, 1999, 27(15): 943-946.

[5] Gao P, Yue S J, Chen H T. Carbon emission efficiency of China’s industry sectors: From the perspective of embodied carbon emissions[J]. Journal of Cleaner Production, 2021, 283: 124655.

[6] Zhao P J, Zeng L G, Li P L, et al. China’s transportation sector carbon dioxide emissions efficiency and its influencing factors based on the EBM DEA model with undesirable outputs and spatial Durbin model[J]. Energy, 2022, 238: 121934.

[7] Shao H Q, Wang Z F. Spatial network structure of transportation carbon emission efficiency in China and its influencing factors[J]. Chinese Journal of Population, Resources and Environment, 2021, 19(04): 295-303.

[8] Li J X, Cheng Z. Study on total-factor carbon emission efficiency of China’s manufacturing industry when considering technology heterogeneity[J]. Journal of Cleaner Production, 2020, 160: 121021.

[9] 范建平，肖慧，樊晓宏. 考虑非期望产出的改进EBM-DEA三阶段模型——基于中国省际物流业效率的实证分析[J]. 中国管理科学, 2017, 25(08): 166-174.

[10] 银西阳，贾小娟，李冬梅. 农业产业集聚对农业绿色全要素生产率的影响——基于空间溢出效应视角[J/OL]. 中国农业资源与区划, https://kns.cnki.net/kcms/ detail/11.3513.S.20220129.1448.016.html.

[11] 吕明元，孙献贞，陈维宣. 供给侧结构性因素对产业生态效率影响的实证研究——基于中国纺织业的DEA-Tobit分析[J]. 科技管理研究, 2018, 38(06): 240-245.

[12] Zhao H L, Lin B Q. Assessing the energy productivity of China’s textile industry under carbon emission constraints[J]. Journal of Cleaner Production, 2019, 228: 197-207.

[13] Lin B Q, Bai R. Dynamic energy performance evaluation of Chinese textile industry[J]. Energy, 2020, 199: 117388.

[14] Gai Y X, Qiao Y B, Deng H J, et al. Investigating the eco-efficiency of China’s textile industry based on a firm-level analysis[J]. Science of the Total Environment, 2022, 833: 155075.

[15] 范莉莉，江玉国. 基于熵值法的钢铁企业低碳竞争力评价[J]. 软科学, 2016, 30(08): 42-46.

[16] 曹阳，胡继亮. 调整工业结构发展三峡低碳经济——以湖北省宜昌市为例[J]. 长江流域资源与环境, 2012, 21(01): 17-23.

[17] 苗成林，孙丽艳，杨力. 能源消耗与碳排量约束下区域技术效率研究[J]. 科研管理, 2016, 37(02): 1-8.

[18] 朱磊，张建清，孙元元，等. 环境治理约束与中国经济增长——以控制碳排放为例的实证分析[J]. 中国软科学, 2018, (06): 163-171.

[19] 马飞，胡江艳，孙启鹏，等. 中国省际物流业碳排放绩效测度及驱动因素研究[J]. 生态经济, 2021, 37(09): 27-33+39.

[20] 王恩旭，武春友. 基于超效率DEA模型的中国省际生态效率时空差异研究[J]. 管理学报, 2011, 8(03): 443-450.

[21] 曹炳汝，邓莉娟. 长江经济带物流业效率增长影响因素[J]. 经济地理, 2019, 39(07): 148-157.

[22] 刘华军，郭立祥，乔列成，等. 中国物流业效率的时空格局及动态演进[J]. 数量经济技术经济研究, 2021, 38(05): 57-74.

[23] 董梅，李存芳. 中国低碳技术效率、技术差距与低碳化进程研究——基于MinDS-Luenberger方法的实证分析[J]. 华东经济管理, 2020, 34(11): 81-89.

[24] 邵帅，范美婷，杨莉莉. 经济结构调整、绿色技术进步与中国低碳转型发展——基于总体技术前沿和空间溢出效应视角的经验考察[J]. 管理世界, 2022, 38(02): 46-69+4-10.

[25] 王兴民，吴静，白冰，等. 中国CO2排放的空间分异与驱动因素——基于198个地级及以上城市数据的分析[J]. 经济地理, 2020, 40(11): 29-38.

[26] 牛亚文，赵先超，胡艺觉. 基于NPP-VIIRS夜间灯光的长株潭地区县域土地利用碳排放空间分异研究[J]. 环境科学学报, 2021, 41(09): 3847-3856.

[27] 高新才，韩雪. 黄河流域碳排放的空间分异及影响因素研究[J]. 经济经纬, 2022, 39(01): 13-23.

[28] 韩传峰，宋府霖，滕敏敏. 长三角地区碳排放时空特征、空间聚类与治理策略[J]. 华东经济管理, 2022, 36(05): 24-33.

[29] 薛晖，郑中华，谢启伟. 基于多种DEA模型和Gini准则的效率评价方法——兼对我国高校运营绩效的评价[J]. 中国管理科学, 2014, 22(4): 98-104.

[30] 李少惠，韩慧. 我国省域公共数字文化服务供给效率空间分异及驱动因素研究[J]. 图书情报工作, 2021, 65(7): 67-77.

[31] Anselin L. Local indicators of spatial association——LISA[J]. Geographical Analysis, 1995, 27(2): 93-115.

[32] 刘华军，王耀辉，雷名雨. 中国战略性新兴产业的空间集聚及其演变[J]. 数量经济技术经济研究, 2019, 36(07): 99-116.

[33] 刘华军，郭立祥，乔列成，等. 中国物流业效率的时空格局及动态演进[J]. 数量经济技术经济研究, 2021, 38(05): 57-74.

Research on the Spatial and Temporal Variation of Carbon Emission Efficiency in Textile Industry based on Multi-DEA-Gini

MA Yu-chao, ZHANG Yong-lin

(School of Management, Wuhan Textile University, Wuhan Hubei 430200, China)

Based on the panel data of textile industry in 30 provinces (municipalities, autonomous regions) in China from 2010 to 2019, the carbon emission efficiency of textile industry was measured by using multiple DEA models combined with Gini criterion, and its spatial-temporal differentiation characteristics were revealed by using global trend analysis, exploratory spatial data analysis and standard deviation ellipse technology. The results show that during the observation period, the carbon emission efficiency gap of textile industry in all provinces of China is obvious, and there is an agglomeration trend; The carbon emission efficiency of textile industry showed an inverted "U" trend in both east-west and north-south directions, and the gap narrowed (widened) in east-west (north-south) direction. The carbon emission efficiency of textile industry has shown a significant positive spatial autocorrelation since 2017. The location distribution of carbon emission efficiency of textile industry changed from northeast-southwest to southeast-northwest, and the distribution center moved southward. Finally, some policy suggestions are put forward based on the research findings.

textile industry; gini criterion; carbon emission efficiency; spatial and temporal variation

马玉超（1970-），女，教授，硕士，研究方向：绿色供应链管理.

F425

A

2095－414X(2022)06－0015－09