二级EMI滤波器磁场近场耦合效应研究
杨湘木 王 会
(珠海格力电器股份有限公司 珠海 519070)
引言
电源EMI(Electromagnetic Interference,电磁干扰)滤波器是抑制传导电磁干扰常用手段之一。然而,实测电源EMI滤波器,性能与理论预期相差甚远,造成这种情况的主要原因有:滤波器件的寄生参数,如电容器的引线电感或者电感器的绕组自电容等;印制电路板(PCB)形式的EMI滤波器,板子走线本身的高频寄生效应[1]; 最后,滤波器布局紧密,器件之间不可避免的存在着较大的近场耦合效应的影响,电磁耦合现象也将影响滤波器的高频性能。综上,为了更准确的评估和预测电源EMI滤波器在150 kHz~30 MHz频率范围内抑制传导电磁噪声的能力,有必要将以上影响因素考虑进设计之中[2]。
目前,对于滤波器的研究主要集中在对关键器件的高频寄生效应研究上,通过提高器件的高频性能来改善电源EMI滤波器的插入损耗[3]。面向器件之间耦合效应影响的研究相对较少,且大都是基于电路理论,耦合系数的选取具有经验性、主观性,无法全面表征材料磁导率、磁饱和特性、线圈形状尺寸、线圈位置和距离等因素的综合影响[4]。
本文以二级EMI滤波电路为例,系统研究了器件间近场耦合效应的机理,建立了器件之间耦合的高频模型,并通过分析器件之间近场耦合量的分布,将器件之间的耦合关系和相互影响通过添加互感系数的方式与整个滤波电路相结合,建立了考虑器件间近场耦合效应的仿真电路模型,避开了人工解耦的繁杂。最后,通过将滤波器插入损耗的仿真计算结果与测试结果相对比,表明近场耦合效应对滤波器性能影响显著,同时验证了本文近场耦合建模方法的正确性和可行性。
1 电源EMI滤波器近场耦合的基本原理
1.1 激励电流下近场耦合分析
近场耦合效应可以在相邻元器件上产生感应电压,此感应电压产生的感应电流可以通过传导的方式直接耦合到临近器件,而且,这部分噪声电流的频率范围通常在150 KHz~30 MHz内,因此,传导干扰预测模型需要将近场耦合的影响考虑进去。
近场耦合包括磁场耦合和电场耦合。研究表明,对于滤波器件间的近场耦合作用,磁场耦合比电场耦合的影响更为严重[5];并且,在实际使用中,用来描述电场耦合作用的等效电容比滤波电感器件自身的寄生电容要小很多[6],所以,电场耦合效应对滤波性能的影响可以忽略,对于EMI滤波器的近场耦合分析以磁场耦合为主。磁场耦合指的是磁性元件产生的磁场可以在周围闭合导体上产生感应电压,此感应电压产生的感应电流可以通过传导的方式直接耦合到临近器件。
本文研究的单相电源EMI滤波器的结构和电路形式如图1所示,该滤波器为二级滤波,其中,主要滤波元器件有共模扼流圈、跨接于零火线间的X电容和零火线与地之间的Y电容。

图1 二级电源EMI滤波器
当共模电流流经扼流圈时,由于扼流圈的共模分量较大,共模分量的磁通在磁芯中形成回路,且Y电容的容值一般较小,因而扼流圈与Y电容之间的近场耦合效应可以忽略不计[7],仅需考虑两个扼流圈之间的近场耦合效应;当差模电流流经扼流圈时,磁路无法通过环形磁芯闭合,部分磁通通过周边的空气形成回路,即产生了漏磁通,且X电容的容值一般较大,因而此时除了扼流圈之间存在耦合作用外,扼流圈与X电容之间的近场耦合效应也将会影响电源EMI滤波器的性能,在实际应用中必须予以考虑。
器件之间存在的耦合特性在电路模型上可以用元件间的互感参数M来表示。综上,该二级滤波器考虑近场耦合的电路模型如图2所示。X电容与不相邻扼流圈之间距离较远,且有其他器件相隔,二者之间的耦合作用非常弱,为方便分析,在此忽略。

图2 二阶滤波器近场耦合示意图
1.2 近场耦合电路解耦
互感M存在于两个元件之间,要分别对它们进行直接测量是不可能的。倘若对包含两个元件的网络进行测量,然后从测量的网络参数数据中推导互感则是可行的[9]。如图3将X电容与电感解耦模型等效为一个T型网络,首先测量端口1和端口2的S参数,根据阻抗参数(Z参数)和散射参数(S参数)的变换关系,由测量的S参数计算出电容器支路的阻抗Z3,最终确定M。进一步的,根据表达式(5)求出互感系数K:
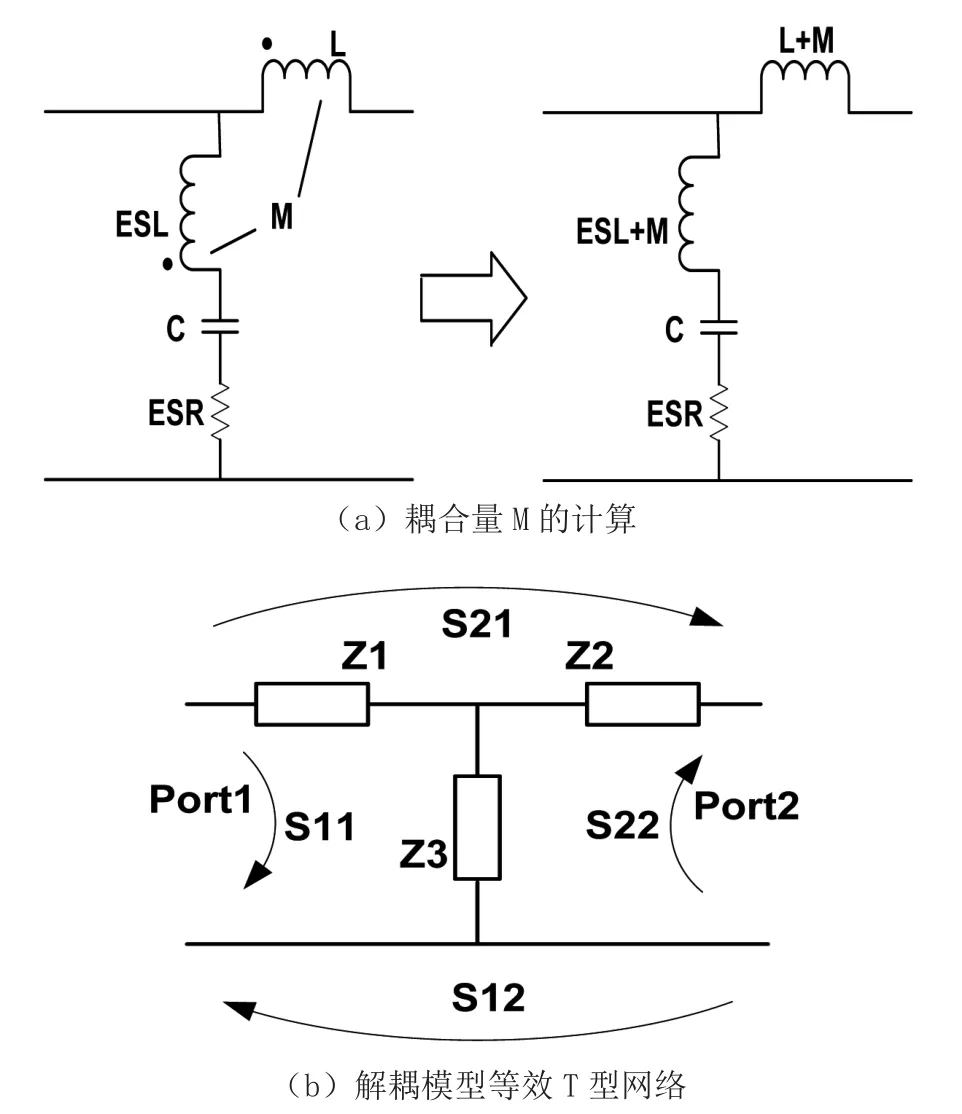
图3 基于S参数解耦示意
其中,为参考阻抗值,一般为50 Ω。
2 电源EMI滤波器的电磁计算模型
2.1 近场磁耦合系数提取
2.1.1 共模扼流圈三维模型的建立
电源EMI滤波器中主要的磁场源是共模扼流圈,首先需要建立扼流圈的三维模型。在以往的设计经验中,可以通过直接建模,优点是模型能够最大程度的反应扼流圈螺旋绕多匝漆包线的特征信息,计算精度高,缺点是受限于扼流圈本身的结构特征,直接建模过于复杂,耗时耗力,且由于扼流圈绕组至少几十匝,导线相对较细,导致有限元网格数量太多,一般不适用于长期的工程应用;另外,对扼流圈还可以简化建模,主要手段是将多匝线圈合并为完整的几何结构处理,见图4。“线包”的处理方式虽然能够节省建模的难度,并可大大降低电磁仿真计算的要求,但简化的“线包”模型却往往不能正确的反应扼流圈的漏磁通影响,由此带来的误差很大。
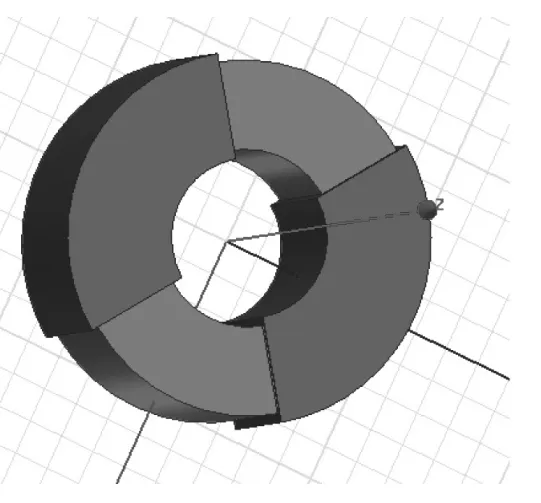
图4 扼流圈模型的简化处理
本文中,扼流圈模型的建立采用PEmag软件包,从软件自带的模型库中取出需要的磁芯形状及绕组形式等信息来完成二维建模,如图5所示,阴影部分代表磁芯,绿色部分代表隔离层。本文研究的扼流圈的具体参数见表1,最后根据磁芯的磁化曲线(如图6)对磁芯材料进行编辑。

图5 扼流圈二维模型

图6 磁芯磁化曲线

表1 扼流圈参数信息表
自动生成的扼流圈三维模型如图7所示。可以看出,Pemag已将扼流圈两个绕组的螺旋线结构简化为相同圈数的单匝闭合线圈,两组绕组在磁芯上形成的包围角度一致。这种处理方式就能够真实反映扼流圈漏磁通的情况,保证了仿真的精度,同时使拥有复杂几何结构的扼流圈模型建立得以简化。

图7 扼流圈三维模型
2.1.2 扼流圈之间的互感计算
在Maxwell 3D中建立两个扼流圈之间的近场耦合模型见图8所示,将两个扼流圈分别命名为group1、group2,通过调节激励方向,分别完成二者之间差模、共模两种形式的近场耦合量的计算。

图8 两个扼流圈互感仿真模型
计算结果如图9所示。可以看出,差模电流激励下,两个器件之间的互感量M=-2401.15 nH;共模电流激励下,两个器件之间的互感量为M=-29.76 nH。计算结果中的正、负号分别代表正耦合和负耦合的情况。

图9 Maxwell中两个扼流圈互感计算结果
可以看出,共模激励下扼流圈之间的互感量相对于其自身的磁场特性来说很小,因此不会对实际滤波性能产生影响,为方便计算,共模激励下扼流圈之间的磁场耦合效应无需考虑。综上,在建立电源EMI滤波器性能预测模型时,只需要考虑差模模式下磁场耦合效应的影响。本文接下来基于差模滤波特性做进一步分析验证。
2.1.3 扼流圈与X电容之间的互感计算
当电容器的摆放位置与扼流圈位置较近,电容器的寄生电感就会不可避免的耦合到扼流圈磁芯产生的漏磁场,从而影响其滤波性能。图10所示是X电容的结构特征,实际能匝链外部磁场的面积仅仅是极板底部与引脚之间构成的环路,用阴影表示。这是因为,X电容内部为圈绕结构,铝箔或银箔分层交替连接电容两级,当漏磁方向与电容内部电场方向共面时,该圈绕结构并不在两极产生电压;当漏磁方向与电容内部电场方向垂直时,每层金属箔内部产生环流,也不在两极感应电压。因此对该部分模型建立时用等尺寸的金属块简化代替。
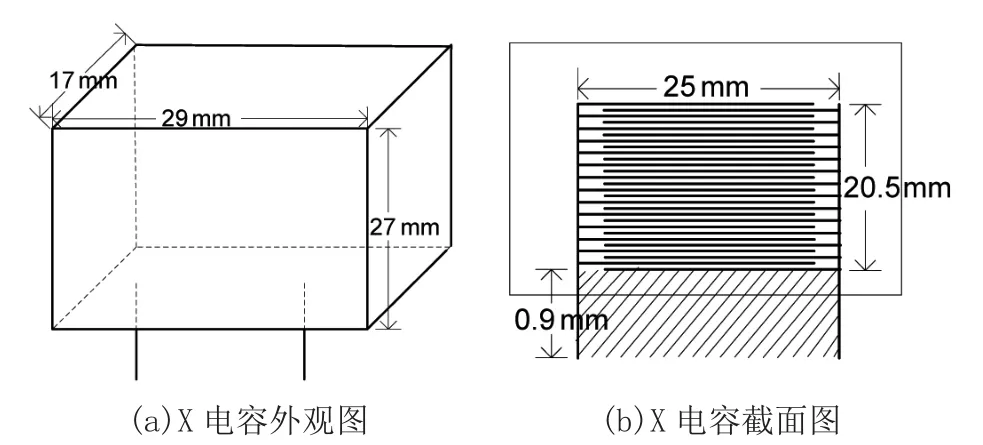
图10 X电容几何结构
按照电容器结构特性建立如图11所示的简化电磁模型,扼流圈与电容器之间相距14 mm。扼流圈绕组和电容器中加入相同的差模电流激励,并分别命名为group1和current1。完成扼流圈与X电容之间差模激励下磁场近场耦合计算,如图12所示,两个器件之间的互感量为M=25.8 nH。
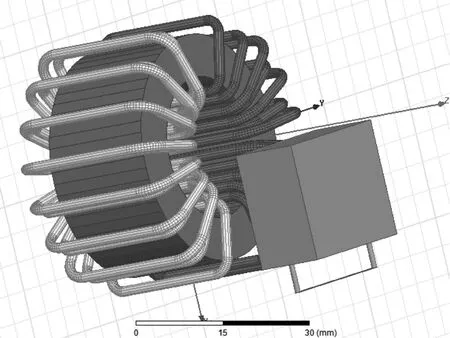
图11 扼流圈与X电容互感仿真模型

图12 扼流圈与X电容互感计算结果
2.2 滤波元件电路模型参数提取
对于滤波元器件的高频模型,可以基于实验测量的方法,根据阻抗分析仪的测试结果,结合相应等效电路模型进行参数拟合来建立。
电容器的等效电路模型可简化为RLC串联网络,如图13所示:ESL为电容器等效串联电感,它包括电容器的绕线电感、内部引线电感和导线电感;ESR为等效串联电阻。最终,得到电容的等效电路参数见表2。

图13 X/Y电容等效电路模型
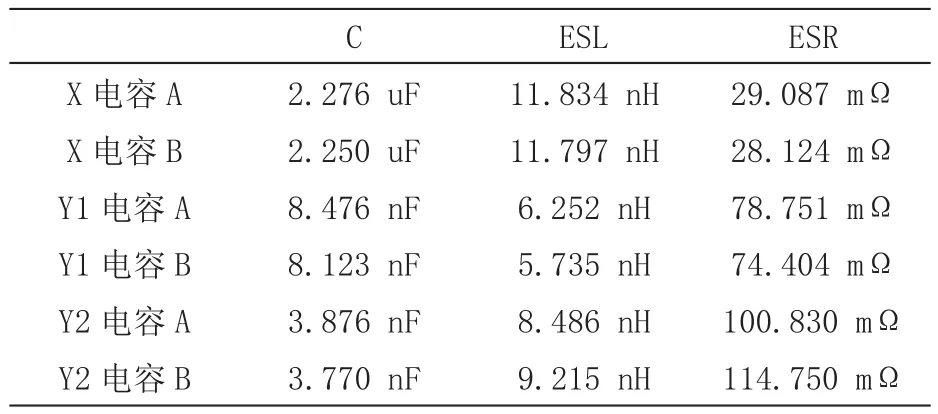
表2 电容模型参数
共模扼流圈的等效差模模型需要考虑线圈的差模电感、绕组交流电阻、电感磁滞和涡流损耗、两个绕组间的寄生电容以及匝间电容,分别以Ld、Rac、Rd、C2、Cd表示。本文研究的电源滤波器工作电流在20~25 A,选用较粗的线径(1.6 mm)绕制扼流圈,表面积较大,且出于散热考虑,导线间距在0.5 mm以上,因此绕组铜线由于趋肤效应和临近效应导致的交流电阻Rac很小,与感抗相比可忽略不计,最终建立其差模等效电路模型如图14所示,等效电路参数见表3。

图14 共模扼流圈差模等效电路模型

表3 共模扼流圈模型参数
因此,根据公式(5),扼流圈之间互感系数K=-0.266;扼流圈与相邻X电容之间互感系数K=0.08。
2.3 PCB寄生参数提取
电源EMI滤波器的PCB的寄生参数在高频时对滤波器性能有很大影响,本文通过Q3D Extractor对PCB寄生参数进行数值分析。图15为由参数提取结果导出的PCB的部分元(PEEC)等效模型,该模型用来反映PCB板布局布线等因素的影响。

图15 PCB寄生参数的PEEC模型
3 仿真与实验验证
3.1 器件间近场耦合量计算方法的验证
为验证器件间近场耦合效应电磁计算模型的正确性,本文将滤波器中共模扼流圈和X电容的等效电路模型、元器间近场耦合系数以及PCB寄生参数模型,按照图16所示的电路结构连接起来,元器件间的近场耦合作用已经通过耦合系数K加载到电路之中,对其端口S参数进行计算,源端和负载端阻抗均为50 Ω。

图16 差模仿真电路模型
利用矢量网络分析仪测试该结构差模端口下的S参数,如图17所示。将测试曲线与本文模型进行对比,结果如图18所示。其中,实线代表实际测量得到的曲线,点线代表未考虑元器件间近场耦合效应的差模仿真曲线,长虚线代表考虑近场耦合效应的差模仿真曲线。通过与测试曲线对比,可以看出,考虑近场耦合效应后的求解结果与实测结果接近,证明本文提出的器件间近场耦合量的计算方法正确可行;同时三条曲线对比后也能看出,考虑器件间近场耦合效应在该结构S参数分析中是非常有必要的。
图17 扼流圈与X电容滤波结构S参数测试
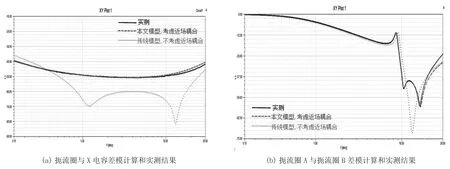
图18 计算和实测结果
3.2 电源滤波器差模滤波性能验证
对于图1中的典型二级EMI滤波器,为了预测差模插入滤波性能,按照上文分析方法将关键滤波器件等效电路模型、元器间近场耦合系数以及PCB寄生参数模型搭建完整的电源滤波器差模模型如图19所示,并使用矢量网络分析仪对滤波器测试其端口的差模传输特性,源端和负载端阻抗设置为50 Ω,最终结果如图20所示。实线是实测结果,长虚线是考虑近场耦合效应计算结果,点线是未考虑近场耦合效应计算结果。对比可知,在整个传导干扰测量范围内150 kHz~30 MHz,近场耦合效应对滤波器差模衰减性能影响非常大,尤其是在1 MHz之前的低频段,由于耦合引起了谐振效应,由此可见分析近场耦合作用是预测滤波性能的关键工作。最后,应用本文提出的方法考虑器件间近场耦合效应后,仿真得到的电源EMI滤波器差模插入损耗与测量结果吻合良好,使得差模插入损耗预测精度提高了约20 dB。

图19 EMI滤波器差模仿真电路

图20 滤波器差模计算与实测结果
4 结论
本文深入研究了二级EMI滤波器,通过对磁性器件精确建模,分析其磁场近场耦合效应机理;最终在提取PCB寄生参数及元器件高频等效电路模型的基础上,建立了考虑器件之间近场耦合效应的电源EMI滤波器性能预测模型,通过将计算结果与实测结果比较,验证了该电路模型的正确性与有效性,从而为电源EMI滤波器对电子设备传导干扰影响的深入研究奠定了基础。

