小学数学单元复习课深度学习:理解—迁移—创新
——以苏教版五上“多边形的面积”单元复习课为例
包春霞
(古田县凤埔中心小学,福建 古田 352200)
小学数学复习课必须以实现学生高阶思维发展为旨归,对单元知识进行有意义地联接与整合。通过“知识理解”层面的目标设定,引导学生对已学知识的回顾与反思,达成对数学基础知识、基本技能的深度理解和掌握;“知识迁移”的目标设定,着眼于知识理解的拓展与勾连,通过对核心知识关键要素的判断和把握,触类旁通,在新的问题情境中判断差异并迁移运用数学原理、解题思路;而“知识创新”旨在引导学生在富有挑战性的问题情境中,突破常规的方法,产生创造性的思路和方案,从而拓展学生对已学知识的认知,形成新认识、新经验,促进学生创新意识和实践能力的发展。笔者以苏教版五年级上册“多边形的面积”单元复习课为例,截取其中的教学片段,从三种知识形态“知识理解”“知识迁移”“知识创新”[1]层面,试析在深度学习背景下如何上好复习课。
一、知识理解:构建概念体系,聚焦核心问题探究
基于深度学习的小学数学单元复习课,首先,要引导学生对所学知识进行回顾梳理与反思,关注对知识的本质、类属以及相关联知识的理解、领悟与组织,构建单元概念体系。其次,强调对知识的灵活应用。知识的理解不能脱离知识的应用,应用是理解的必要环节,通过应用才能达到对知识的真正理解。因此,复习课要依托问题情境,提出引发学生深度思考的关键问题,组织学生围绕关键问题进行深度探究。
[片段一]
学生回顾梳理已经学过的长方形、正方形、三角形、平行四边形和梯形等平面图形的面积计算,明确组合图形是“由两个或两个以上的基本图形组合成的图形”的基本概念。之后,教师揭示课题“多边形的面积复习”,引导学生进行探究。
教师可出示题目:
拍卖一块土地,起拍价每平方米2 万元,一家开发商要想获得这块土地,至少要准备多少万元?
(1)出示问题:这块土地的形状是一个组合图形(如图1),怎样对图形进行合理分割或添补?一共有几种方法?小组讨论交流,并在学习单上完成。
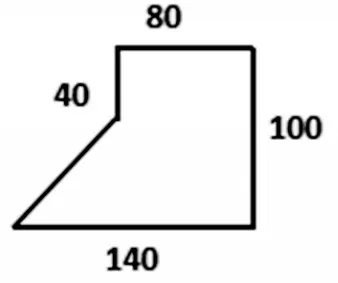
图1
(2)全班反馈交流,汇总得出分割或添补的几种方法(如图2)。

图2
(3)讨论并思考:
其一,比较①②③④四种方法,它们的解题思路有什么不同?
学生通过讨论,明确不同之处在于:方法①②③是通过“分割求和”,把多边形的面积转化为两个基本图形面积之和;方法④是运用“添补求差”,把多边形的面积转化为长方形与梯形的面积之差。教师要让学生明确:转化的路径不同,解决问题的方法也不同。
其二,计算方法不同,但它们在解题策略方面有什么相同之处?
学生通过质疑反思,感悟多边形的面积计算都是运用转化的思想,通过图形的等积变形,运用“分割”“添补”等方法,把多边形转化为两个基本图形面积之和或差,化未知为已知,求出多边形的面积。
其三,教师结合⑤⑥⑦强调解题方法的优化,让学生认识到要把多边形尽可能转化为基本图形个数最少的面积之和。同时,教师要引导学生注重图形分析,根据给出的条件合理推算出其他必要的数据。
(4)请选择其中的一种方法,列式解决问题。
教师小结:计算多边形面积的方法是多种多样的,可以通过“分割求和”“添补求差”等方法把多边形转化为基本图形的组合,再结合具体的问题情境,选择计算多边形面积的最优策略。
学习多边形的面积计算,有助于扩展学生对图形的认识,体现多边形与基本图形的关系,发展学生的空间观念。在具体教学展开的过程中,教师通过对核心问题的提炼,驱动学生的深度思考,是实现深度学习的有效途径。该环节的教学,教师通过精心创设的开放式问题情境,梳理回顾了多边形面积转化为基本图形面积的计算方法,同时,在对多种方法的思辨、比较中,增强学生解决问题的优化意识,引导学生从基础知识和数学技能两个方面对多边形面积的计算进行梳理。学生通过层层质疑、步步比较,优化策略,温故而知新,强化了分析图形、合理推算数据的基本技能。如此,学生超越简单的具体知识,深入理解学习内容,提高了运用所学知识解决实际问题的能力。
二、知识迁移:引导多元反思,感悟数学思想
以深度教学为指向的数学复习课,要着力于培养学生在“知识理解”的基础上,把所学的知识、形成的基本技能迁移到不同的情境中去,解决与数学知识相关的现实情境问题。复习重在引导学生感悟数学知识背后的数学思想、方法和价值意义,帮助学生获得经验的生长和数学素养的提升。[2]该单元所学的求组合图形的面积是求多边形面积的“种子课”,是具有迁移性、生长性的关键课。运用转化的思想,通过割、补、移等方法求多边形面积,对于后续学习更复杂的多边形面积具有迁移价值。
[片段二]
出示题目:校园里有一块草坪(如图3 左),中间有人行道穿过。你会求出这个草坪的面积吗?(单位:米)

图3
学生尝试独立解决。教师展示学生不同的解法。(如图4~5)

图4

图5
教师让学生分别说明以上两种方法的解题思路。如,第一种解法是先求出两条人行道的面积,再从总面积里减去人行道的面积,求出草坪的面积,计算过程繁复。第二种解法是通过平移化整,把四块草坪的面积转化为长是(15-1)米,宽是(11-1)米的长方形的面积(如图3 右)。
引导比较:你喜欢哪种方法?你能给第二种方法起个名字吗?(平移化整)
教师小结:在解决实际问题时,除了分割法、添补法可以求多边形的面积,还可以通过“平移化整”,把分割后的几部分图形组合成一个基本图形。
学生在“分割求和”“添补求差”这两种基本方法的学习中,初步形成了分与合的数学思想,明确多边形可以分解成基本图形,基本图形也可以组合成多边形,形成综合与分析的解题思路。本环节的教学,教师通过引导学生对分与合思想的迁移运用,触类旁通,灵活运用整体思维,把四个分散的梯形小草坪的面积“平移化整”,转化为一个长方形的面积,丰富了学生对求多边形面积方法的认识。
三、知识创新:突破常规思路,培育高阶思维
深度学习的根本目的就是发展学生的高阶思维。指向深度学习的数学复习课可着力于通过“知识创新”激活学生的思维,引导学生突破常规的方法,解决稍复杂的实际问题,生成超越教材规定内容的数学知识或方法,形成新认识、新经验,帮助学生形成数学学科特有的理解问题和分析问题的思维方式,促进学生高阶思维的发展。
[片段三]
在挑战自我环节,教师出示:双山小学有一块直角梯形的花圃(如图6)。其中①②两个是等腰三角形,分别种月季和玫瑰,③种牡丹。你能求出这个花圃的总面积吗?
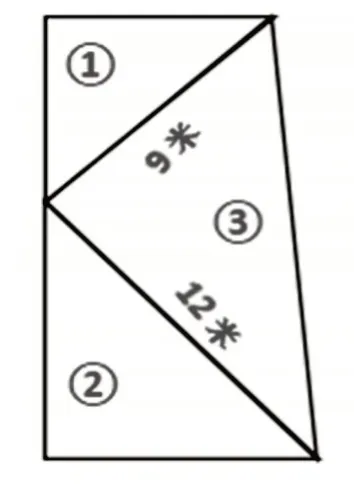
图6
要求这个花圃的总面积,要先分别求出①②③三个直角三角形的面积。由①②是等腰直角三角形可推出③也是直角三角形;已知两条直角边可求出牡丹园③的面积。此题的关键是求出①②两个等腰直角三角形的面积。而要求等腰直角三角形的面积只要已知其中的一条直角边。如何把9 米或12 米转化为新图形的一条直角边呢?
教师可组织学生讨论,并启发:能否通过添补法进行转化,把三角形①转化为直角边为9 米的等腰直角三角形面积的一半,进而求出它的面积?
学生讨论,画图尝试(如图7)。显然,三角形①的面积是直角边为9 米的等腰直角三角形面积的一半。其他学生受到启发,用同样的方法,把三角形②转化为直角边为12 米的等腰直角三角形面积的一半,最后求得总面积。

图7
最后,教师引导学生反思:“做完这道题你们有什么新的收获?”一位学生深有体会地说:“添补法表面上看很简单,却能用它来解决复杂的实际问题。”
从学生的角度而言,有深度的教学就是让学生进行深度思维的教学。[3]在“知识理解”层面,学生已经掌握用“添补法”解决简单多边形的面积。该环节中,教师通过创设富有挑战性的学习情境,引导学生灵活运用“添补求半”的方法,把等腰直角三角形斜边转化为新等腰直角三角形的直角边,化未知为已知,进而创造性地解决非常规性问题。学生在富有思维张力的解题活动中,感悟数学基本方法的魅力,实现知识和思维的同步发展。
深度学习为指向的小学数学复习课,以实现知识理解、知识迁移和知识创新为层层进阶的教学目标,通过整理与复习力求让学生对已学知识理解深刻,感悟透彻;同时,通过对知识的迁移运用,真正与学生原有知识发生深刻的交融,能够顺利地进行迁移和运用,解决一些常规性的复杂问题;最后通过解决一些较复杂的实际问题,突破常规的方法,引导学生深入知识的背后获取知识背后丰富的思维价值,从而使学生的思维不断深化。

