精心设计核心问题 助力学生深度学习

蔡鹭燕

（厦门市集美小学，福建 厦门 361024）

短短的一堂课内如何实现有效教学？用核心问题来统摄知识点极为重要。所谓核心问题，即数学教学中的中心问题、基本问题，它既能激发与促进学生自主活动，又能整合课堂的关键内容和重点内容，还能贯穿整节课的任务或问题。［1］

如果说教育是为思维而教，那么数学教学就是为数学思维而教。适当的“问题引领”正是实现学生深度学习、促进思维发展的重要途径。［2］学生学习本身就是一个复杂的过程，需要教师在课堂上设计出好的核心问题，来将这个复杂的过程变成一个探索的、思考的、有意义的学习过程，可见“核心问题”的设计的重要性。

一、追溯知识本质，设计核心问题

教师往往清楚每节课的知识重点是什么，但是在设计问题时，往往浮于表面，不能有效引导学生深入探究和理解数学知识本质，当学生面对具有挑战性的问题，一时答不上来或没答到点子上时，教师就直接以一句“你是不是这样想的……”来化解自己认为的“教学困境”，这实际上是让学生被动地去接受知识，学生不能真正地了解知识的本质。

例如，《11-20 各数的认识》是人教版一年级上册的内容，它既是前面10 以内数的认识的延伸，又是后面认识较大数的基础。教师通过阅读教参和其他书籍，能很快地找出本节课知识的重点和难点是初步感知“十进位值制”的计数方法，体会“十进位值制”的简洁方法。那么教师如何发现并确定该课的核心问题？数起源于数，学生已经认识了10 以内的数，一个一个数是我们之前认识数的方法，那么，该节课要认识的11-20 各数，数量越来越大，如果再一个一个去数，学生会觉得很麻烦，于是“为什么要把满十根的小棒捆成一捆”就成了该节课的核心问题。

于是笔者在教学《11-20 各数的认识》时，创设了古人计数的情境。

情境一：从前有两兄弟，他们每天都会到山上打猎。第一天，打猎归来，老大高兴地对老二说：“我今天打了6 只羊”。老二说：“哥哥，哥哥，我今天打了5只羊呢。”（图1）

图1

问题1：老大和老二说得对吗？请你认真数一数。

情境二：第二天，打猎归来，老大指着地上的13块小石头，兴奋地对老二说：“老二，你快看，我今天打了13 只山鸡呢！”老二一听，可坐不住了，对老大说：“我打的山鸡比你多，我打了14 只呢！”（图2）

图2

问题2：你能最先判断出谁说的是正确的，为什么？

情境三：第三天，打猎归来，老二打了17 只羊，老大打了15 只羊。

问题3：你能用你手中的小棒表示老大、老二打的羊的只数，让别人不用数，一眼就看出哪份是老大打的，哪份是老二打的呢？

问题1 激活了学生已有的知识经验，一个一个数10 以内的数，问题2 让学生切身体会到“十进位值制”的简洁性，产生“可以把10 个一当成1 个十”的心向，最后问题3 激发了学生的创造，让学生自然而然用“十进位值制”表示11-20 各数。这三个子问题串联起来，解决了“为什么要把满十根的小棒捆成一捆”这个大的核心问题，指向教学内容的本质用“十进位值制”表示11-20 各数，促使学生去经历数学知识“再创造”的过程。

二、探析学生认识错误点，设计核心问题

教师课前应探析学生认识错误点，根据这些错误点设计有针对性的“核心问题”，就能把课堂教学中的差错融化为一种教学资源，化腐朽为神奇［3］，促进学生全身心地融入创造性学习活动中，感受数学学习的乐趣。

教学《倍的认识》前，笔者让学生试着用图表示自己心目中的倍。学生会出现以下几种误解：一是认为倍是独立存在的，忽略倍是两个量之间的比较。二是以为把谁看成标准，不需要把所有的都看成一份。于是，顺着学生认识的错误点，围绕“倍是什么”这一核心问题进行教学，笔者进行了以下问题设计：

问题1：单独出示3 个苹果，问：你能说一说苹果是谁的几倍吗？为什么？

问题2：再出示6 个梨，请你通过圈一圈说明梨和苹果有怎样的倍数关系？

问题3：第一位同学（见图3）是把一个苹果看成了标准，第二位同学（见图4）是把所有的苹果当成了标准，到底谁的想法合理呢？

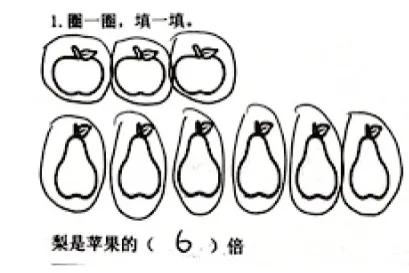
图3

图4

通过问题1，学生都认为只有苹果一种东西，是不能说出谁是谁的几倍的，直击学生的误区一，接着问题2 的提出，引发学生去通过圈一圈的方式，自主寻找倍的关系，暴露学生错误的认识点，最后问题3的提出，激起学生思维火花的碰撞，去反思自己想法的合理性，直击学生的误区二，通过这三个问题的串联，解决了“倍是什么”这个大的核心问题，层层递进，激起了学生探究的欲望和思维碰撞的火花。

三、理清操作活动目的，设计核心问题

在新课标引领下，很多教师已越来越关注学生学习方式地转变，如课堂上教师都会依实际需要组织学生开展必要的操作活动：一是激发学生数学学习的兴趣，二是化抽象为直观，将数学规律外显，助力学生探索知识的内涵，促进学生深度学习。但是，也经常发现教师在设计操作活动环节时只注意引导学生怎么做，而忽略引导学生思考为什么这么做，即忽视了操作活动中核心问题的设计，导致学生停留在表面的操作。

例如，笔者听过这样一堂课，教师在教学《平行四边形的面积》时，教师很用心地设计给小组分配不同形状的平行四边形，让小组合作去剪一剪、拼一拼来将平行四边形转化成长方形，却未能引导学生认真地去思考：怎么剪？为什么这么剪？

笔者认为，在让学生进行剪一剪、拼一拼的活动前，应围绕核心问题：怎样把平行四边形转化为学过的图形（长方形）？平行四边形与转化后的图形之间有哪些联系？来引发学生边操作边思考，建立“动手”和“动脑”之间的良好的协作关系。笔者建议可以进行如下问题设计：问题1：你是怎么剪的？问题2：为什么剪出来的必须是直角呢？问题3：平行四边形与转化后的图形什么联系？问题1 先引发学生去回顾自己的操作过程，问题2 引发学生去思考为什么要沿着高剪，找到如何剪才能更准、更快、更省事，最后问题3，引发学生深层次思考，使学生通过去寻找转化后的图形与平行四边形之间的联系，来达到证明平行四边形的面积等于底乘高这一操作目的。这样融“核心问题”于活动中，让学生的小组合作更具有目的性和实效性。

学贵有疑，疑问是促使思考、深化学习的催化剂。课堂中教师适时用核心问题引领教学，把准学生的思考方向，就能提高学生的思考高度，促使学生进行深度学习。巧妙地于知识本质、学生认识错误点、操作活动目的这三处设计核心问题，能使教师的问更有深度，更具广度，促使学生更有探索的欲望，小组合作探究也更有时效性和目的性。