均匀能流密度槽式聚光器设计及光学特性
赵 芳, 蒋 波, 程道来
(1.上海应用技术大学 城市建设与安全工程学院, 上海 201418; 2.上海应用技术大学 机械工程学院, 上海201418)
0 引言
太阳能聚光器能将反射镜上大面积的光线聚焦起来,再反射到接收器上,可以实现低成本提高光斑能流密度的目的。然而在聚光过程中,接收器会出现聚焦光斑能流密度分布不均匀、 局部温度过高的现象[1],[2],这不仅影响接收器的光电的转换效率,而且还影响接收器的使用寿命,因此研制聚焦光斑能流密度分布均匀、 光学性能高的聚光器具有重要意义。
聚光系统对能流密度分布均匀性有较高的要求, 为了使接收器上聚焦光斑能流密度分布足够均匀,学者们对聚光系统进行了改进[3],[4]。江守利[5]提出了一种等光强分布的折平板反射聚光器。 孙后环[6]改变了接收器的形状以此来获取均匀分布的光斑。 荆雷[7]通过等光程原理和柯勒照明原理将二次反射和折平板相结合, 设计了能够实现均匀照度的光伏聚光器。 Yang[8]通过平面镜阵列法对聚光器的轮廓进行了重新设计以实现太阳能电池板上的光斑能流密度均匀分布。 Wang[9]通过改进聚光器和增加光谱分频器来提高光伏电池片表面的能流密度均匀性。 以上研究均是通过改变接收器的形状或增加二次反射装置, 以损失较多光通量为代价实现接收器上能流密度均匀分布。
本文根据聚光系统的光线反射路径, 利用几何构造法和微元法设计出两种结构紧凑、 聚焦光斑能流密度分布均匀的非成像聚光器, 在光通量损失较少的情况下, 使接收器上能流密度分布均匀,在选取最优模型的基础上,利用蒙特卡洛光线追踪法(Monte Carlo Ray Tracing, MCRT)分析了光线入射方式、几何聚光比、接收器安装误差和系统跟踪误差对接收器上光斑能流密度均匀分布的影响。
1 聚光器设计
1.1 构建几何模型
传统的抛物面聚光器将光线聚焦到一条焦线上,而非成像聚光器是将光线聚焦到一个区域。根据给出的接收器宽度W、高度H 和几何聚光比C的关系, 运用光线跟踪法对聚光系统进行光学分析。 利用微元法与几何构造法来求解非成像聚光器曲面的点阵坐标公式。 图1 为聚光器光路示意图。 由图1(a)可以看出,两侧聚光器反射光线在接收器上无交叉, 单侧聚光器反射光线聚焦到同侧半边接收器上。 由图1(b)可以看出,单侧聚光器光线反射到整个接收器宽度区域, 两侧聚光器反射光线在接收器上交叉重叠。 显然这两种光线路径都符合边缘光线原理, 为了方便区分这两种聚光器,将图1 中(a)和(b)两种聚光器分别命名为Ⅰ型和Ⅱ型聚光器。

图1 聚光器光路示意图Fig.1 The schematic diagram for the light path of the concentrator
本文将微元法与几何构造法相结合, 设计能够实现接收器上能流密度均匀分布的非成像聚光器。 将聚光器沿宽度方向在x 轴上的投影进行等分,与接收器上相对应等分区域建立映射关系。根据已知聚光器内表面初始反射点和接收器的位置关系, 计算聚光器内表面下一反射点在y 轴上的坐标, 再根据y 轴坐标来计算得到该点在x 轴方向上坐标, 依此步骤计算内表面反射点在x 轴和y 轴方向的点阵, 最后得到聚光器内表面所有点阵的x 轴和y 轴坐标。
1.1.1 聚光器两侧反射光线在接收器上无交叉重叠根据微积分理论, 将接收器沿宽度方向划分n 段,每段宽度为Δw=W/2n。每段对应的平均能流密度分别为i1,i2,i3,…,in。 由能量守恒定律可得:
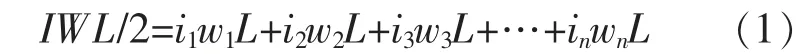
式中:I 为接收面的平均能流密度;W 为接收器宽度;L 为接收器的长度。由于该接收器上接收面的能流密度分布处处相等,每个单元大小相等,因此该接收面每段光线聚焦到的能量都相等,存在:

图1(a)中P,Q 两点分别为接收器的两个边界点,点A1(W/2,0)为聚光器内侧反射面的起始点,其横坐标等于边界点Q 的横坐标。 点A2与点A1之间的关系为

式中:C 为几何聚光比。
点A3与点A2之间的关系为

根据式(4),(5)依次类推聚光器内侧反射面上点A4,A5,…,An的坐标,得到Ⅰ型聚光器内侧反射面的末端点An坐标为

从式(6)~(9)可以看出,接收器的高度、宽度与几何聚光比可以描述Ⅰ,Ⅱ型聚光器形状,假设接收器的宽度固定, 可以根据所需几何聚光比来确定Ⅰ,Ⅱ型聚光器的形状。
1.2 聚光器结构尺寸
对聚光器系统中接收器高度、 宽度和几何聚光比赋值,代入式(6)~(9)中,通过MATLAB 求解,并将求解的点阵坐标导入软件中建模,同时对抛物面聚光器y=x2/4H 赋相同参数值进行建模。图2 为3 种聚光器反射面计算结果。
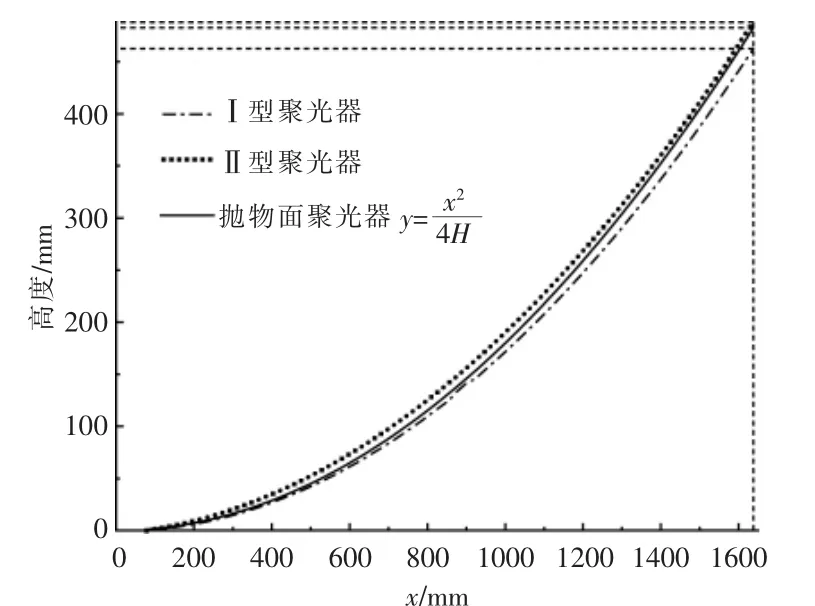
图2 3 种聚光器反射面Fig.2 Reflectors of three types of concentrators
从图2 中可以看出, Ⅱ型聚光器的槽深要比另外两种聚光器的槽深要深, 并且Ⅱ型聚光器的曲率要比Ⅰ型聚光器和抛物面聚光器的曲率大,由于3 种聚光器的槽深和曲率不一样, 将会导致3 种聚光器的聚光性能存在差异。
2 仿真与结果分析
利用Trace Pro 光学追踪软件对聚光器进行光线追踪分析,设置光源为长方形的格点光源,光源强度为637 W/m2, 光线波长设为0.546 1 mm,聚光器表面的反射率为0.95, 接收器的吸收率为1, 为了保证光线模拟精度, 将光线总数设置为9.9×107条,同时将光束的入射方式分别设置为平行光源和日照分布两种形式, 分别探究聚光器在平行光线下和太阳光照下, 反射到接收器上的能流密度分布的均匀程度。
2.1 接收面能流密度分析
图3 为3 种聚光器反射到W=156 mm,H=1 390 mm,C=20 的接收器表面的光斑能流密度二维分布。由图3 可以看出,无论在平行光还是太阳光入射下,与抛物面聚光器相比,本文所设计的Ⅰ型和Ⅱ型聚光器其接收器上能流密度分布的均匀程度均有明显改善,且能流分布区域也明显增大。

图3 接收器表面能流密度分布Fig.3 Energy flux density distributions of the receiver surface
图4 为接收器水平中心线的能流密度分布曲线。 对于抛物面聚光器,当平行光入射时,接收器能流分布区域的宽度为78.13 mm,中心处能流密度峰值为110 kW/m2,向两侧迅速衰减为0;当太阳光入射时, 接收器能流密度峰值为91 kW/m2,能流分布区域为93.5 mm。 由此可知,抛物面聚光系统中接收器能流密度分布均匀性较差, 且接收器能流分布区域较小,能流密度梯度较大。 此外,太阳光照下接收器受光照区域比平行光照下大,这是因为太阳光比平行光多一个0.267°的“光锥角”[11],导致太阳光入射聚光器的入射角比平行光入射角大, 造成抛物面聚光器反射出的光线反射角也比平行光的反射角大, 使太阳光线比平行光线从接收器中心向两端扩散程度大, 增加了受光照区域。
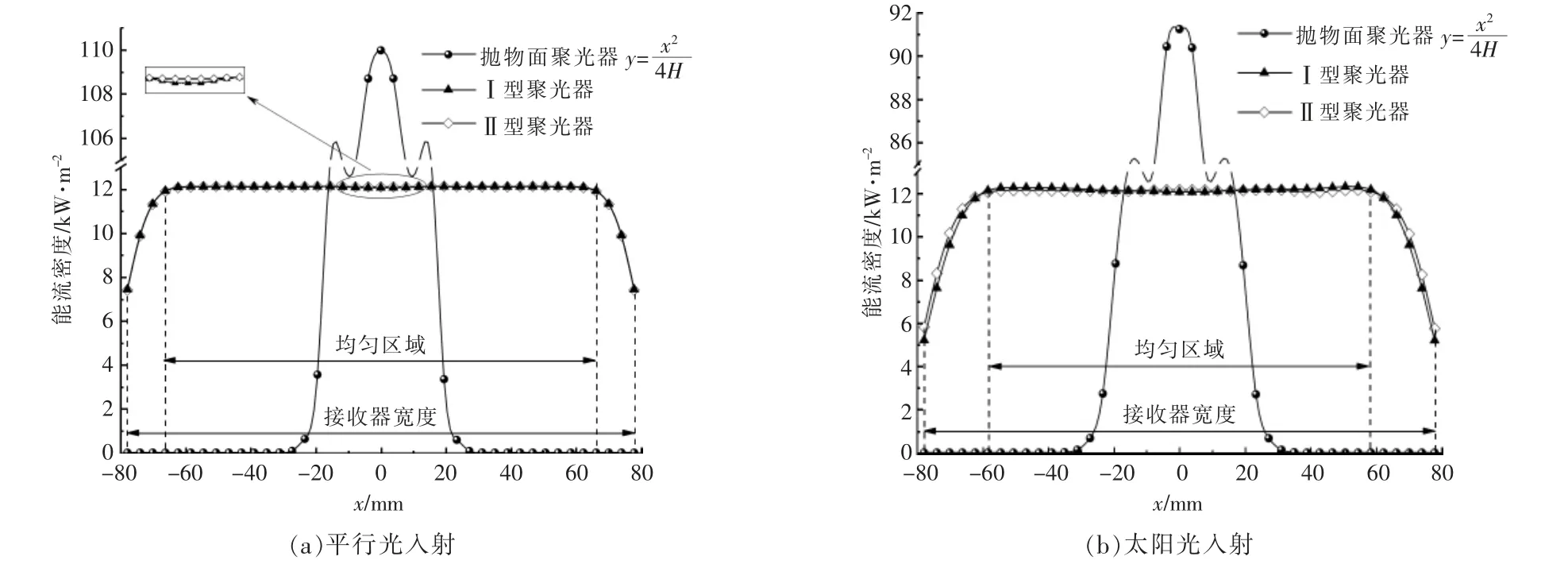
图4 3 种不同聚光器接收器在水平中心线(y=0)处能流密度分布Fig.4 Energy flux density distributions at the horizontal centerline (y=0) for three different concentrator receivers
由图4(a)可知,平行光入射条件下,经Ⅰ型聚光器聚光后, 接收器上能流密度整体分布比较均匀,约为12 kW/m2,但中间区域(x=-11~11 mm)能流密度值出现微小波动,波动范围较大,然而,对于Ⅱ型聚光器, 接收器能流密度分布在区域内(x=-62~62 mm)内没有明显波动,均匀程度更佳。此外, Ⅱ型聚光器反射到接收器上两侧边缘的能流密度比Ⅰ型聚光器边缘处高, 说明Ⅱ型聚光器从接收器两侧溢出的光线比Ⅰ型聚光器少, 且匀光效果和光学效率均优于Ⅰ型聚光器, 证明了Ⅱ型聚光器计算模型的合理性和有效性。
由图4(b)可知,当太阳光入射时,在x=-62~62 mm 区域内, Ⅱ型聚光器反射到接收器上的能流密度比平行光入射时波动幅度大, 但仍小于Ⅰ型聚光器接收器能流密度的波动幅度。此外,在太阳光入射下, 两种聚光器所对应的能流密度均匀区域均减小,这是由于太阳光的“光锥角”,造成部分光线从接收器的两侧边缘区域溢出, 导致两侧边缘区域能流密度下降, 两侧边缘不均匀区域扩大。 同时,在太阳光入射下,Ⅰ型聚光器反射到接收器边缘的能流密度依旧比Ⅱ型聚光器要小,说明Ⅱ型聚光器在太阳光入射下的光学特性依旧优于Ⅰ型聚光器。
图5 是聚光比为20, 宽度为156 mm 的接收器在不同高度所接收到的光斑能流密度分布。 由图5(a)可知,当平行光线入射聚光器时,经过Ⅱ型聚光器反射到接收器上能流密度曲线分布足够均匀。经过Ⅱ型聚光器反射到接收器上,接收器在不同高度所对应的能流密度曲线基本重合, 而Ⅰ型聚光器在不同高度对应的能流密度曲线重合度相对较差。Ⅰ、Ⅱ型聚光器在平行光线下反射到接收器两侧边缘能流密度值比太阳光线反射到接收器两侧边缘密度值大。
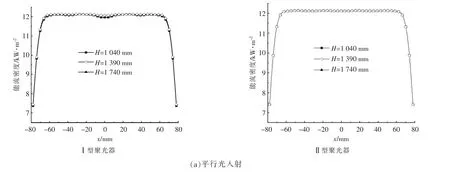
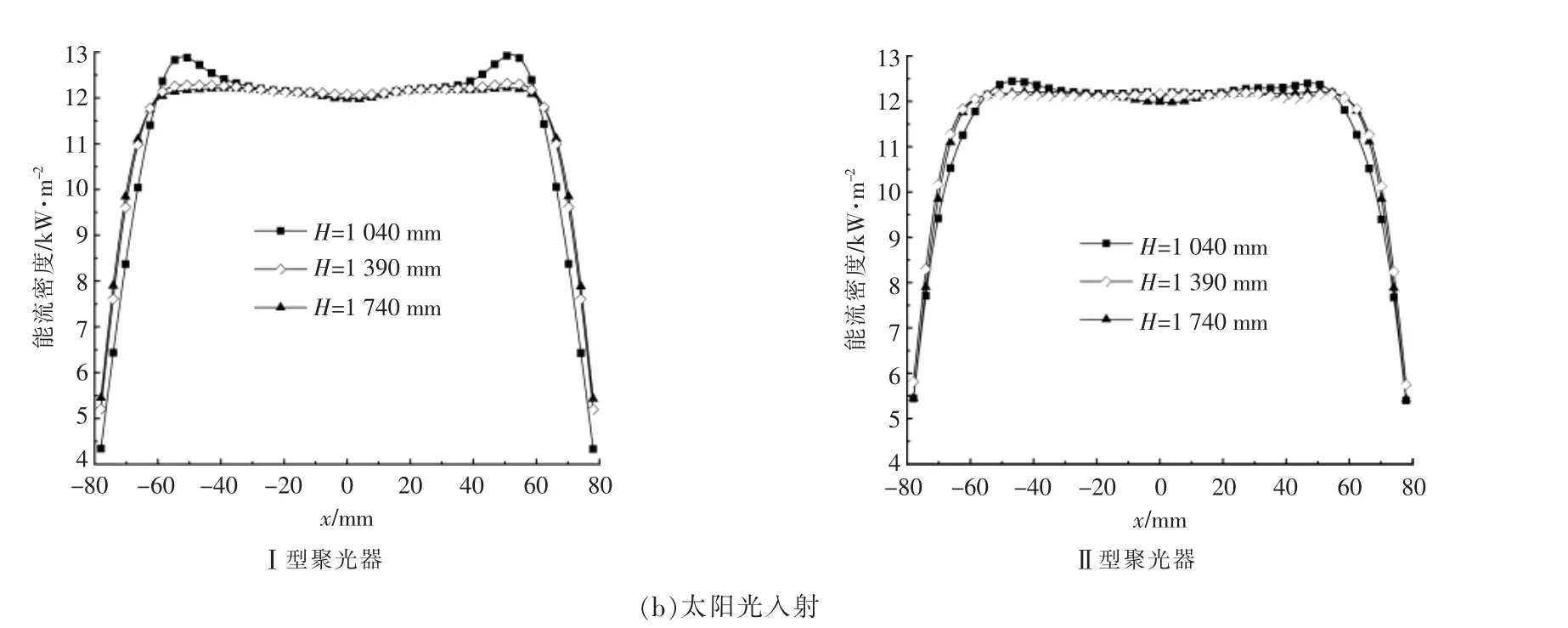
图5 接收器水平中心线(y=0)处能流密度分布Fig.5 Energy flux density distributions at the horizontal centerline of the receiver (y=0)
由图5(b)可知,太阳光线入射时,在不同高度的接收器所对应的Ⅱ型聚光器, 其反射到接收器上的能流密度分布曲线出现波动, 但是其波动幅度小于Ⅰ型聚光器。 Ⅰ型聚光器反射到接收器上的能流密度分布非常不均匀,并呈现中心下降,两端上升的趋势, 这是由于太阳光线不是平行光线,而是含有0.267°的“光锥角”所导致的。 由前文可知, Ⅱ型聚光器的高度高于Ⅰ型聚光器的高度, 所以Ⅱ型聚光器内表面边缘的反射角大于Ⅰ型聚光器内表面边缘的反射角。 由于入射太阳光线的偏离角很小, 造成边缘区域光线偏离接收器表面的能量小,导致能流密度呈现较小的突变。考虑到太阳光线的光学特性, Ⅱ型聚光器更适合太阳聚光。
通过对比传统的抛物线型聚光器及本文设计的Ⅰ,Ⅱ型聚光器的光学特性,可以得出,Ⅱ型聚光器聚光性能优于Ⅰ型聚光器。 在平行光及太阳光入射两种工况下, 光线在不同的接收器安装高度下, 经Ⅱ型聚光器聚光后接收器能流密度均匀分布区域更大,能流密度分布均匀程度更佳,波动幅度更小,边缘地区光线泄漏较少。
2.2 聚光器参数的敏感性分析
采用MCRT 对Ⅱ型聚光器进行光学模拟,并对其光学特性进行分析, 探讨其在不同几何聚光比、 不同误差条件下的光学效率和对几何聚光比参数的敏感性。
2.2.1 几何聚光比对电池板接收器能流密度的影响
聚光器的水平截面面积与接收器面积之比称为几何聚光比[10],其为聚光能力提供了一个量化标准, 一般认为聚光比越高则相对应的聚光器的性能就越好。由于几何聚光比的不一致,导致接收器上接收到的能流密度分布不同。
图6 为W=156 mm,H=1 390 mm 时, 不同几何聚光比接收器水平中心线能流密度分布。 由图6(a)可知,平行光入射时,虽然MCRT 的性质造成左右两侧接收器上能流密度存在微小的差距,但是接收器上的能流密度几乎是对称分布的,且分布依旧非常均匀。 几何聚光比在10~20 时,接收器上能流密度均匀分布区域逐渐增大, 几何聚光比在20~30 时,能流分布区域的大小随着几何聚光比的增大而逐渐减小。由此可见,在一定范围内,几何聚光比对光斑偏移量影响显著,当几何聚光比为20 时,其能流密度均匀分布的区域宽度为125.08 mm,占接收器区域的80.18%,此区域能流密度值为12 kW/m2,此时聚光器的光学聚光比为18.8。
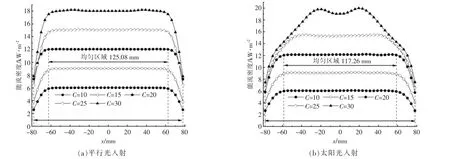
图6 不同几何聚光比下接收器水平中心线(y=0)处能流密度分布Fig.6 Energy flux density distributions at the horizontal centerline(y=0)of the receiver under different geometric concentration ratios
由图6(b)可知,当太阳光入射时,几何聚光比在10~25 时,接收器上能流密度分布均匀性极佳,并且与平行光线入射时理论分析的趋势一致。几何聚光比为20 时,接收器上的能流密度均匀分布最大,其均匀分布的区域宽度为117.26 mm,占宽度为156 mm,接收器宽度区域的75.17%,此区域能流密度值为12 kW/m2,此时聚光器的光学聚光比为18.2。 当几何聚光比为30 时,聚光器的匀光效果明显不佳,这是因为太阳产生的“圆盘”效应,随着聚光比增加,造成太阳光线从接收器溢出的光线也就越多, 导致两侧能流密度分布均匀效果显著下降。
通常把接收器接收到的光通量与聚光器上接收到的光通量比值称之为光学效率[11]。 图7 为不同几何聚光比下接收器光学效率。 在相同的参数条件下, 平行光入射的效率始终比太阳光入射的效率要高。 在不同几何聚光比下,平行光的光学率均达到了94%以上,其主要的损失是由于平行光束在反射面的损失和少部分光线从接收器两侧边缘溢出所造成的。 几何聚光比为20 时,聚光器的性能为最佳。

图7 不同几何聚光比下接收器光学效率Fig.7 The optical efficiency of the receiver under different geometric concentration ratios
2.2.2 不同光学误差特性分析
在理想条件下, 整个聚光系统在跟踪系统的作用下始终无误差地指向太阳、 接收器在高度方向上安装精确, 但在实际情况中聚光系统在跟踪方向和接收器安装上都存在误差。 本节讨论当W=156 mm,H=1 390 mm,C=20 时,聚光器系统存在一定的跟踪误差和安装误差对于接收器上光斑能流密度分布的影响。
聚光系统中存在跟踪误差会导致接收器上入射光线方向发生偏移, 偏移的光线会直接影响接收器上的能流密度分布, 并进一步影响光电转换效率, 因此对跟踪误差进行量化是衡量聚光器性能的一个评判标准。 图8 为跟踪误差为5,10,15 mrad 时,接收器能流密度的分布。由图8(a)可知,随着跟踪误差α 的增大,能流密度曲线发生了整体偏移, 这是因为大角度的平行光入射后会导致大角度的反射光,造成过多的光线泄漏,导致接收器的光学效率降低。同时跟踪误差增大,光线入射角增大,使光线反射路径增长,造成扩散现象更明显,导致反射光线辐射的区域更宽,辐射中心区域的能流密度升高。 由于接收器的宽度始终为156 mm, 接收器在接收边缘处的光线溢出接收器,导致边缘处能流密度减小,两侧不均匀区域扩大,能流密度均匀分布的区域宽度从109.29 mm 降低至58.84 mm, 导致均匀区域占比从70.06%降至37.72%。 同时反射光线不再是平行光入射聚光器,而是以一定角度入射聚光器,此时接收器的能流密度曲线不再保持对称, 正方向和负方向边缘缓冲区域的占比增大, 接收器上均匀光斑的宽度随着跟踪误差的增大而逐渐减小。
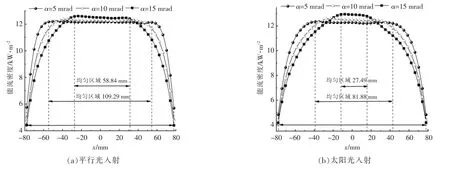
图8 不同跟踪误差下接收器水平中心线(y=0)处能流密度分布Fig.8 Energy flux density distributions at the horizontal centerline of the receiver (y=0) under different tracking errors
由图8(b)可以看出,接收器上能流密度均匀分布区域随着跟踪误差的增大而减小, 在宽度为156 mm 的接收器上, 能流密度均匀分布宽度从81.88 mm 减小到27.49 mm, 其有效占比从52.49%减小到17.62%,并且均匀分布的区域减小的幅度相对于平行光入射下跟踪误差要大。 这是由于太阳光光线本身就含有一定的“光锥角”,当无跟踪误差的时, 太阳光入射分布均匀的区域比平行光入射时小,随着跟踪误差的增大,向接收器两侧偏离的光线就越多, 两侧溢出接收器的光线也越多, 导致不均匀区域从两侧边缘向中间逐渐增加。
图9 为接收器安装误差ΔH 对能流密度分布的影响。当接收器的安装位置存在误差时,接收器上的聚焦光斑能流密度也会发生变化。 由图9(a)可以看出,由于ΔH 增大,光斑偏移,均匀分布的区域宽度由108.89 mm 逐渐降低至94.05 mm,同时导致接收器上均匀分布区域占比从69.80%降低至60.29%,但是接收器上能流密度的最大值却随着安装误差的增大而逐步增大。 从能流密度变化规律可知, 接收器中心区域的能流密度值随着反射光线在中心辐射区域的增加而逐渐增大。
由图9(b)可以看出,随着安装误差的增加,均匀光斑分布区域逐渐减小, 这是因为接收器的高度增加,导致太阳光入射下最大采光半角减小,均匀分布区域宽度减小, 随着安装误差从3 mm增大至10 mm, 其均匀分布的宽度从101.71 mm降低至85.67 mm,同时造成光斑能流密度均匀分布的区域占比从65.20%降低至54.92%。 光学误差导致接收器上焦点分布区域扩展, 能流密度聚光比降低, 这将需要更大的接收器, 以免光线溢出, 然而过大的接收器会导致较大的辐射和对流损失, 所以本文对于优化过后的Ⅱ型聚光器产生的能量损失是可以接受。
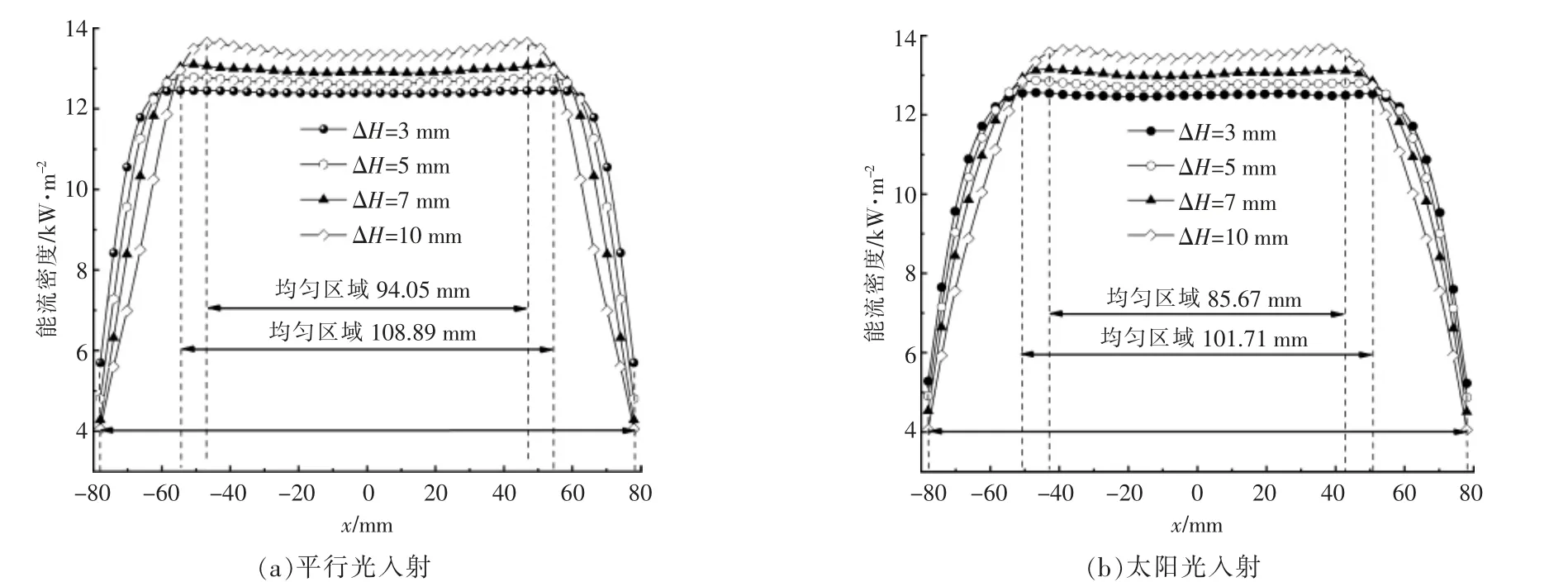
图9 不同安装误差下接收器水平中心线(y=0)处能流密度分布Fig.9 Energy flux density distributions at the horizontal centerline of the receiver (y=0) under different installation errors
3 结论
本文对槽式聚光器进行了优化设计, 结合微元法与几何构造法提出了Ⅰ,Ⅱ型聚光器模型,对其光学特性进行了模拟, 并与抛物面聚光器进行对比,主要结论如下。
①与抛物面聚光器相比,Ⅰ,Ⅱ型聚光器接收器上能流密度分布均匀程度明显提高,其中,Ⅱ型聚光器性能最佳, 其聚光后接收器上能流密度均匀分布的区域最大, 且能流密度分布波动幅度最小,能量密度值集中于12 kW/m2。
②C=20 时,Ⅱ型聚光器光学特性最佳,平行光和太阳光分别入射到Ⅱ型聚光器, 反射到接收器上的光斑能流密度均匀分布的区域都达到最大,分别占总接收器区域的80.18%和75.17%,此时光学效率也达到最大,分别为99%和95%。
③聚光系统中跟踪误差对Ⅱ型聚光器的匀光效果影响较大, 为保证接收器上能流密度均匀分布的区域大,跟踪误差越小越好;接收器的安装误差增大, 接收器上的光斑能流密度仍然保持较高的均匀性,说明安装误差对该聚光器影响较小。

