基于BOPPPS模型培养数学思维的高等数学教学设计——以“定积分的概念”为例

宋彩虹

南京城市职业学院 江苏南京 211200

高等数学作为高等职业院校理工科专业的一门重要基础课程，是面向大学一年级学生开设的必修课。根据高等职业教育人才培养目标，高等数学课程教学需遵循“适度、够用”的原则[1]，即培养适度的逻辑思维、够用的计算能力。通过学习本课程，既能掌握足够的数学知识，又能提升数学核心素养，为后续专业课程的学习和职业发展、终身学习奠定基础，最终达到高等职业教育的人才培养目标。

数学思维是运用数学知识，有条理地进行理性思维、逻辑推理等的一系列思维活动。比如转化与化归、类比、从一般到特殊、从特殊到一般、数形结合、积微成著等思想。数学思维的本质是数学抽象和逻辑推理，所以，也决定了高等数学的学习具有一定的难度。而由于高职院校招生来源的多样性，学生数学基础参差不齐，大部分学生对高等数学课程有畏难情绪，同时，传统的教学模式效果不尽如人意。因此，高职院校的高等数学课程教学改革迫在眉睫。

在高等数学课程教学中，如何设计有效培养学生数学思维、注重数学应用的教学方案，是任课教师需要思考和研究的。文章将BOPPPS模型引入高等数学教学中，并以定积分的概念为例，展示了培养学生数学思维的策略和做法。

一、BOPPPS模型

BOPPPS模型[2]是加拿大广泛推行的教师技能培训体系ISW的理论基础[3]，是一个指导教师拆分并探究教学过程、发现教学盲点、达成教学目标的有效工具。根据学生专注力持续时间(大约15分钟)的规律[4]，把课堂教学过程分为六个模块(也称为六要素)：导入(Bridge-in)、学习目标(Objective)、前测(Pre-assessment)、参与式互动学习(Participatory Learning)、后测(Post-assessment)和总结(Summary)[5-6]。根据BOPPPS模型，课堂教学被分成若干个教学小单元，每个教学小单元(约15分钟)内具有“起承转合”的功能，且每个教学小单元组合而成的课堂也要遵循“起承转合”的脉络[4]。

BOPPPS模型从教学设计结构上给出了遵循“教学目标—教学行为—学习活动—教学评估—教学目标”的教学循环过程，使得教师能够有效地组织课程教学，获得反馈信息[7]；该模式强调以学生为中心的教学理念，在全面了解学情的基础上，从学生的兴趣点和学生能够接受的知识点出发，明确教学目标，以参与式互动学习为核心，通过后测环节发现教学盲点，反馈教学目标达成情况，最后进行总结，整合学习要点，布置课后作业，巩固学习目标。该教学模型有明确的操作步骤，具有非常强的可实施性，它可以使课堂教学设计更加条理化、合理化。

二、BOPPPS模型在“定积分的概念”教学中的应用

定积分的概念是学习定积分的基础，在高等数学中占有重要地位，上承导数和不定积分，下启定积分的计算与应用。BOPPPS模型将本次课堂教学过程拆分为六个模块，具体设计框架见下表：

BOPPPS模型的六个教学模块表

(一)导入(Bridge-in)

本次课的导入环节采用问题形式，教师给出实际问题：“某城市绿化园划拨了一块形状不规则的土地，用于绿化，已知每平方米的绿化费用，请你预算一下绿化的总费用?”这个问题从生活中的实际案例出发，结合定积分的几何意义，从学生已有的知识过渡到新知识，激发学生探求“定积分的概念”这一核心知识的兴趣，强化数学有用的思想。

(二)学习目标(Objective)

教师利用多媒体阐明本节课的学习目标，让学生有目标地参与后续课堂教学中，从而提高学习效率。本节的学习目标：

知识目标：(1)深刻理解定积分的概念；(2)了解定积分概念的发现过程；(3)理解定积分的几何意义和物理意义。

技能目标：(1)掌握求解实际问题的“分、匀、和、精”的数学思想；(2)能利用定积分的几何意义求简单平面图形的面积；(3)能用积分的思想进行简单的数学建模解决实际问题。

素养目标：(1)通过两个引例的求解让学生感受“化整为零、以直代曲、积微成著”的数学思想；(2)培养学生类比、抽象、数形结合等数学思维的能力；(3)结合中华传统文化，提升学生数学文化素养。

(三)前测(Pre-assessment)

教师通过学习通平台布置课前学习任务，发布微积分发展史及刘徽的割圆术的相关微课视频，并提出三个问题：(1)矩形的面积公式？(2)刘徽的割圆术运用了什么数学思想？(3)如何描述极限的定义？

学生观看微课并回答问题，通过前测环节，教师可以了解学生对预备知识的掌握情况、兴趣点和参与度，更好地掌握学生的学情，为参与式互动学习环节做好准备。

(四)参与式互动学习(Participatory Learning)

为解决导入环节的绿化建设预算费用问题，教师引导学生对问题进行转化，通过分析，将问题转化为求封闭曲线所围成的平面图形的面积。利用PPT演示动画：一条不规则的封闭曲线，用两组互相垂直的平行线对其进行分割，如图1所示，所得的图形为曲边梯形和曲边三角形，而曲边三角形可以看作是曲边梯形的特殊情况，最终，把问题转化为求曲边梯形的面积。由此给出第一个引例：

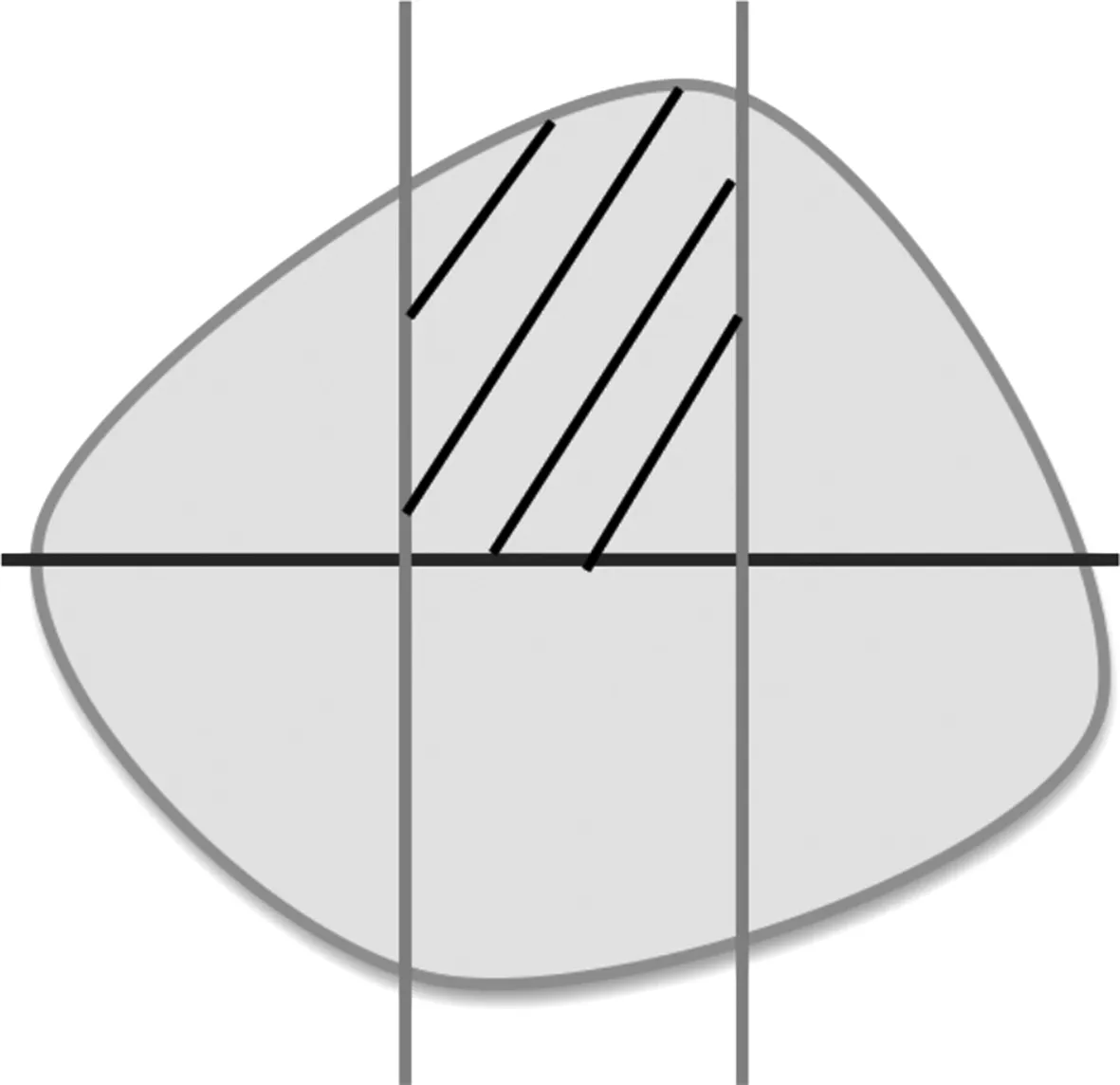
图1

引例1 求曲边梯形的面积？

首先，让学生思考如何利用化归的数学思想，将难的问题转化为易于解决的问题，启发学生学会如何化整为零、以直代曲；接着，教师演示动画，让学生直观地看出:随着区间分割越来越细，分割的小矩形越来越多，每个小矩形的面积就越接近于所在的小曲边梯形的面积，所有小矩形的面积之和就越接近所求曲边梯形的面积；此时，教师向学生提问：结合所学知识，用什么样的数学工具来刻画这一动态过程？最后，教师根据学生的回答，引导学生总结出借助极限求解曲边梯形面积的表达式。然后，教师给出第二个引例：

引例2 求变速直线运动的路程？

利用已知求未知的数学思想，从匀速直线运动的路程入手，引导学生回忆平均速度和瞬时速度之间的关系，进而用“分、匀、和、精”的数学思想，推导出变速直线运动的路程表达式。

最后，教师引导学生进行类比，归纳总结出上述两个引例的共性：一是求解的量具有相同特征；二是解决问题的思想方法和步骤相同；三是都归结为具有同样数学结构的和式极限的计算。进而抽象出一般函数在区间上定积分的定义。然后，教师完整讲解定积分的定义，并引导学生找出定积分与不定积分的区别与联系，为定积分的计算做好铺垫。

教师在围绕教学主线(见图2)实施教学的过程中，需引导学生积极参与、思考和归纳。通过两个引例，使学生了解定积分这一抽象概念的发现过程以及解决类似问题所用到的“分、匀、和、精”的数学思想，理解定积分的几何意义和物理意义，突破教学的重难点。

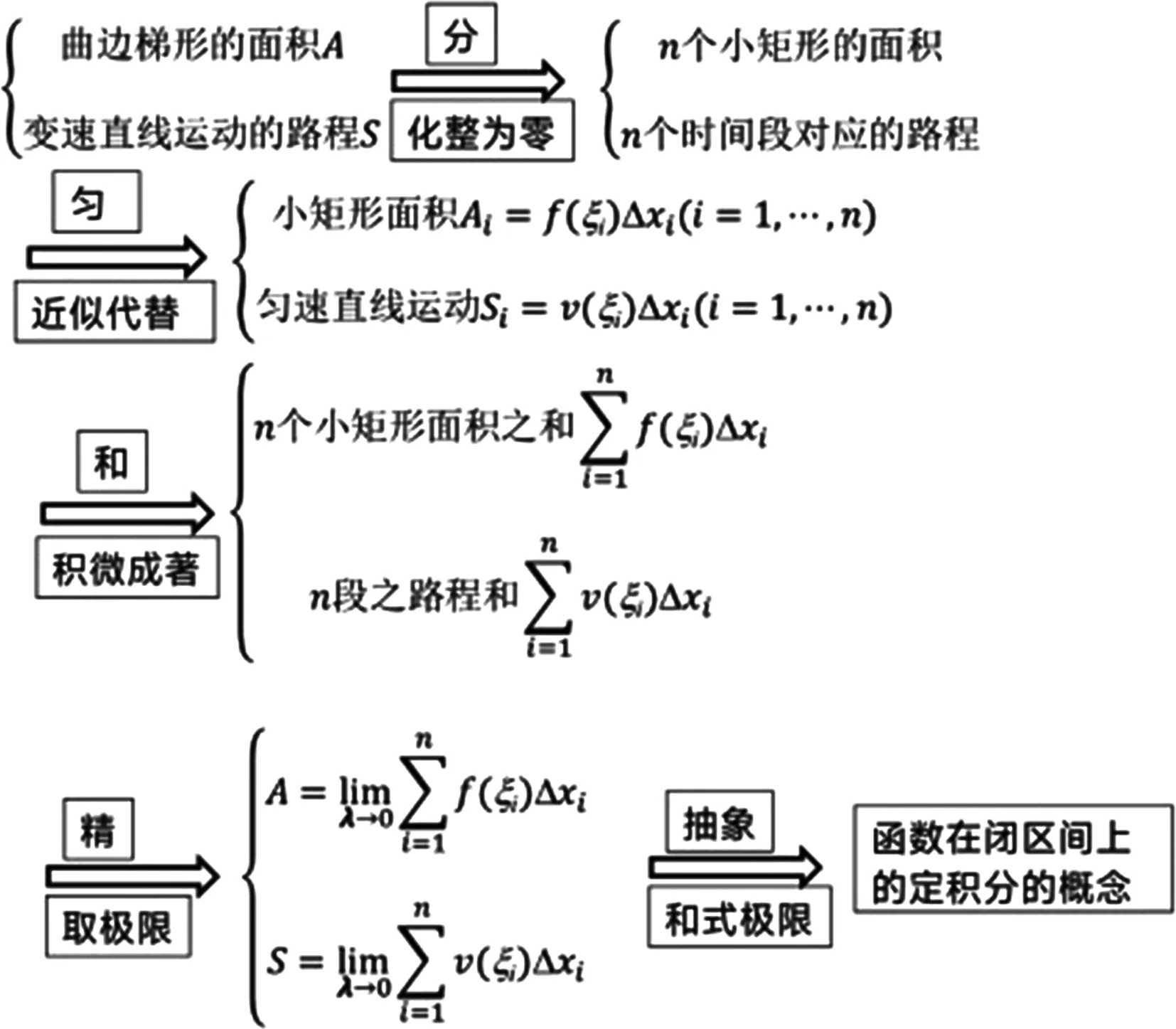
图2 教学主线

(五)后测(Post-assessment)

围绕定积分的概念这一重点，在学习通平台设置后测问题，请学生思考并动手做一做：

(1)用定积分表示出y=x2与x=1、x轴围成的平面图形的面积？

设计意图：本题需要学生利用数形结合的方法，用定积分正确表示出所求平面图形的面积。注意定积分的两要素—被积函数和积分上下限的确立方法。

设计意图：本题主要考查学生如何将定积分转化为对应平面图形的面积的能力。

(六)总结(summary)

本次课学习的主要内容为定积分的概念，从贴近生活的案例出发，激发学生学习的兴趣，从而避免课程枯燥。根据定积分的几何意义，可以通过求对应平面图形的面积来计算出定积分，为下一次课的教学内容——牛顿-莱布尼兹公式的引入埋下伏笔。教师通过布置课后作业，巩固数形结合思想，加深对定积分概念的理解。

三、结论

教师在进行高等数学课程教学设计时，需遵循“必需、够用”为度，“实用、会用”为主的原则，即以理论够用，技能运用为主的原则，教学内容上要弱化严格的论证、繁琐的推导和复杂的运算，强化高等数学的基本知识和技能有用的意识并学会如何应用。具体到应用BOPPPS模型进行高等数学教学设计时要注意：

(1)要以前测环节为前提，全面了解学生学情。可通过问卷、考试、作业、提问或讨论等形式全面了解学情，对不同学情的学生进行针对性的教学设计。从学生的兴趣及能够接受的知识点出发，采用多样化的教学手段，制定一套以学生发展为中心的教学体系。

(2)要确立学生作为参与式互动学习环节的主体地位。教师在设计整个教学过程时，要坚持“以学生为中心”的教学理念，须从传统教学的讲授者转变为引领学生全方位参与探究式学习的领航者，以培养学生主动学习和创新意识。

(3)要以学习目标为核心。导入、学习目标、前测、参与式互动学习、后测和总结，这六个环节都是为有效达成学习目标而开展的教学过程。因此，教师要按照人才培养方案，制定好课程标准，准确把握课程学习目标，开展有针对性的教学设计。而数学思维最终是要运用到不同学科中解决实际问题，因此，教师在进行高等数学教学设计时，可以根据需要，设计与其他学科相关的应用案例，以培养学生将数学思维运用到其他学科专业的能力。这种教学理念可鼓励教师跨越本学科与其他学科之间的界限，更加主动地学习新知识、新理念和新技能，从而有效地提高教师的教学能力和综合素质，进而提升高等数学课程的教学质量。