考虑时间满意度的生鲜前置仓双目标选址优化

0 引言

随着新零售时代的到来，传统生鲜电商的单一线上模式已经难以满足顾客即时配送和生鲜品质等全方位的需求，于是生鲜电商企业开始由单一线上模式转化为线上平台+线下体验的新模式来满足顾客多样化的需求，提出了一种新的仓配模式——前置仓。前置仓是在生鲜货物送往目的地前的最后一个仓库和站点，也是最靠近消费者的一个节点，为了满足分钟级的配送，前置仓的服务半径通常约为3～5公里，采用这种模式能够大幅度缩短生鲜货物的运输时间，尽可能保证商品的新鲜度，提升商品的品质[1-3]。

前置仓属于末端物流配送中心，与传统物流配送中心不同的是，前置仓对时效性要求更高，目前对于前置仓的研究主要聚焦在前置仓模式分析层面上，在具体实施层面上关于前置仓选址问题的研究较少[4]。近年来关于物流配送中心选址问题主要从单目标、多目标及求解算法等方面进行了研究。肖建华等引入了非等覆盖半径的思想建立了生鲜农产品配送中心选址模型并提出了一种基于自适应遗传算法的动态膜进化算法[5]，魏洁等建立了最小距离约束的生鲜农产品多配送中心连续选址模型并设计了由模糊C均值聚类算法与改进模拟退火算法嵌套而成的FCM-ISA算法[6]，Dou等针对冷藏食品易腐烂的特点引入新鲜度和时间窗等约束条件建立了冷链物流配送中心选址问题的数学优化模型，并提出了一种免疫狼群混合算法[7]；随着研究复杂度的提升，有学者将单目标选址问题延伸至多目标选址问题，Zhang等从顾客对生鲜商品需求不确定性的角度建立了生鲜配送中心选址模型并提出了一种改进的果蝇优化算法[8]，宋英华等综合考虑了灾后应急物资动态需求和实际道路状况建立了多周期多目标应急物资配送中心快速选址模型并采用耦合Dijkstra算法的分层序列法进行求解[9]，黄露等针对延误情境下配送中心选址问题提出了双层规划模型，并利用层次遗传算法进行求解[10]。从对配送中心选址的研究成果来看，目前关于选址的模型多为考虑成本的单目标选址模型，且从顾客时间需求的角度来考虑的配送中心选址研究还较少。

基于时效性对前置仓的重要程度，本文将时间满意度引入前置仓选址问题中，建立了配送成本最小和时间满意度最大的双目标优化模型，在传统的遗传算法基础上基于进化逆转的思想提出了进化突变操作并引入了精英保留策略[11]，用于提高遗传算法的寻优能力与收敛速度，最后通过算例对模型和算法进行验证。

1 问题描述及模型建立

1.1 问题描述

本文研究的生鲜前置仓选址问题可描述为，在由前置仓、顾客需求点构成的二级物流网络中，已知顾客需求点的位置与需求量，在满足两个目标函数总配送成本最小和时间满意度最大并达到最优的情况下，从候选点中选出P个前置仓建设点。

1.2 模型假设

（1）每个需求点的顾客对时间满意感知程度是一样的，时间满意度只与配送时间有关且时间满意度函数是呈岭形分布，不考虑因配送时间所造成的生鲜货物的损耗。

（2）每个需求点的位置和需求量已知，并且需求量保持不变，前置仓配送可以直接送达每个需求点，由于前置仓的建设成本为固定成本，所以不必算入成本目标函数中。

（3）配送成本与运输距离成正比，所有生鲜货物的单位距离运输成本相同，且拥有足够的运力进行运输，不考虑竞争因素。

1.3 符号说明

表1 符号含义说明

1.4 配送成本及时间满意度

（1）配送成本

配送成本是由从前置仓运送生鲜货物至顾客需求点所产生的物流运输费用，配送成本与生鲜货物运输量、运输距离、单位运输费用有关。由于本文给出的前置仓与需求点的距离为两点之间的欧氏距离，所以乘以城市道路非直线系数来转换为货物的运输路程。配送成本计算方式如公式（1）所示。

（2）时间满意度函数

时间满意度函数为生鲜货物从前置仓运送至顾客需求点所花费时间的满意程度，当所花费的配送时间越长，满意度就越低。配送时间与配送距离和配送速度有关，配送时间的计算如公式（2）所示，本文选取的是余弦分布时间满意度函数[12]，函数式如公式（3）所示。

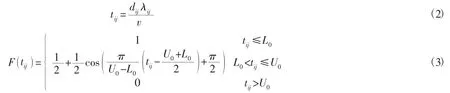
1.5 模型构建

本文建立了配送成本最小和时间满意度最大的双目标优化模型：

约束条件为：

目标函数式（4）表示最小化总配送成本，目标函数式（5）表示最大化总的顾客需求点的时间满意度，目标函数式（6）表示使用极大极小归一化与线性加权处理将双目标函数转化为单目标函数，约束式（7）表示每一个需求点最多只能被一个前置仓服务，约束式（8）表示拟建设的前置仓数量为P个，约束式（9）表示需求点不能被没有选中的前置仓候选点服务，约束式（10）表示需求点的满意度水平达到了α时才能被覆盖，约束式（11）表示每个前置仓所覆盖的需求点的需求量之和必须达到总需求量的β倍，约束式（12）表示总覆盖需求必须达到θ以上，约束式（13）表示对决策变量Xj、Yij的0～1约束。

2 算法设计

针对前置仓选址问题，本文给出了两种前置仓候选点的选取方式并设计出相应的求解方法。第一种为将需求点通过聚类算法进行聚类，将聚类后得到的聚类中心作为候选点，运用CPLEX求解器求解整数规划模型。第二种为将顾客需求点本身作为候选点，由于CPLEX不适合求解大规模问题，所以本文设计了改进的遗传算法对其进行求解。

2.1 K-means聚类算法

利用K-means聚类算法将分散的需求点聚为K簇，将每一簇的聚类中心作为前置仓的候选点，通过MATLAB调用CPLEX对所建立的模型进行求解。聚类操作可以简述为三步：

Step1：首先随机抽取K个需求点作为最初的聚类中心。

Step2：将每个需求点分配到离他们最近的聚类中心，生成K簇。

Step3：对于每个簇，计算出所有被分到该簇的需求点的平均值作为新的聚类中心，重复步骤2和步骤3，当聚类中心的位置不再发生改变时，迭代停止，聚类完成。

2.2 改进的遗传算法

（1）编码及解码操作

编码方式采用的是实数编码，染色体的长度为待建前置仓数量加1，每一段染色体对应着前置仓候选点的编号，0代表所有未能被待建前置仓所服务的需求点集合，例如{9,12,47,68,78,31,64,0}为一个完整的染色体。

染色体解码操作如下：

Step1：判断需求点是否能满足当前染色体下任意前置仓候选点的最低时间满意度约束。

Step2：若无法满足，则将该需求点归为未能被待建前置仓所服务的需求点集合。若能够满足，则查找出大于最低时间满意度的前置仓候选点集合，按照距离远近的划分原则，将需求点分给集合中距离需求点最近的前置仓候选点。

Step3：重复上述步骤直至所有染色体完成解码。

（2）选择、交叉、变异

选择算子操作，通过适应度函数可以评判各个个体的优劣程度，本文的选择算子通过轮盘赌的方式来进行操作，个体的适应度越大，该个体的基因遗传到子代的概率也就越大。

交叉是产生新个体基因的主要来源，交叉的操作如下[13]：

Step1：在任意两个基因之间随机选择两个切点，被选中的两个基因称之为父代1和父代2。

Step2：从父代1中将两个切点之间的基因片段复制给子代1。

Step3：从父代2中排除父代1遗传给子代1的基因，以此避免重复，之后从父代2中按照基因出现的顺序，逐个复制基因给子代1，直到子代1的所有位置被填满。

Step4：将上述操作的父代1和父代2进行角色互换，得到子代2。

交叉操作示例如图1所示。

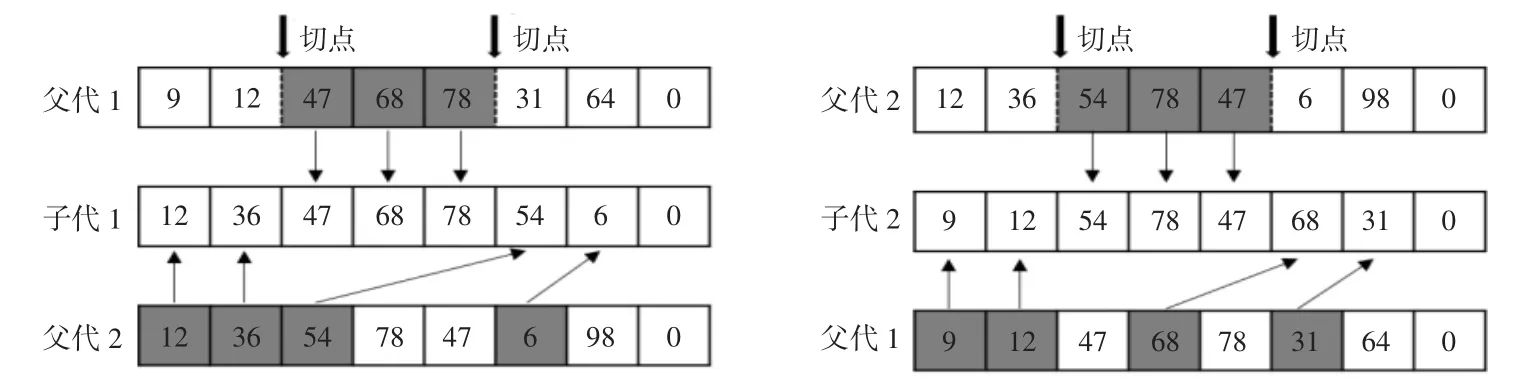
图1 交叉操作示例

变异操作有利于维持种群的多样性，避免算法过早陷入局部最优，变异操作为随机选择两个基本位，按照变异概率将两个基本位上的基因值替换为个体中从未出现过的基因值。变异操作示例如图2所示。

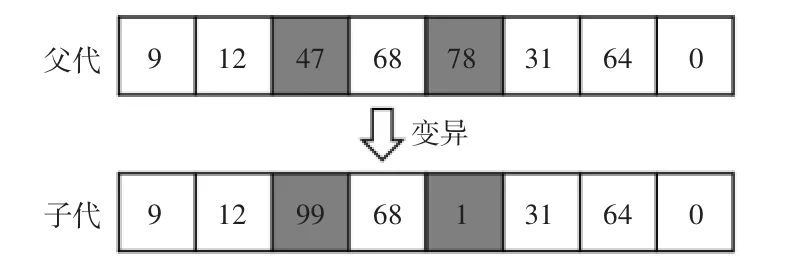
图2 变异操作示例

（3）进化突变

基于进化逆转的思想，本文提出了进化突变操作，进化突变是指随机替换基因个体上的片段，新替换的基因片段为替换之前个体中所没有出现过的基因，进化体现在，当进化突变过后的基因个体适应度变高，则进行突变，否则不进行突变。进化突变示例如图3所示。

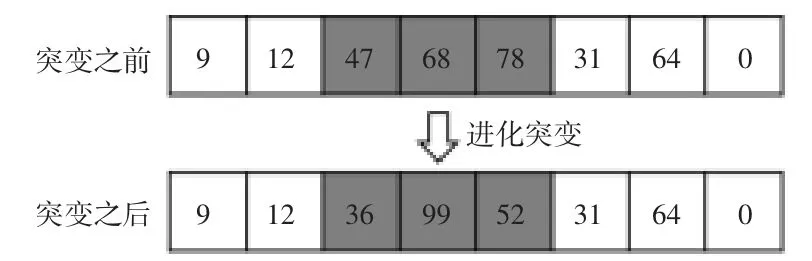
图3 进化突变示例

（4）精英保留

采用精英保留可以确保优良的个体能够保留得以延续至下一代，保证子代不会比父代差，精英保留的操作步骤如下：

Step1：将经过选择、交叉、变异、进化突变操作后形成的子代与父代放在一起，按照适应度高低进行排序，遵循从适应度高到低的选择原则，选择出一定比例适应度高的基因。

Step2：将选择出来的适应度高的基因等量替换步骤1中所形成的子代中适应度低的子代，此时重新形成的子代为真正的子代，精英保留操作完成。

3 数值实验

3.1 实验设计

本文通过算例来证明模型和改进的遗传算法的有效性以及候选点选取方式的优劣性，算例的需求点坐标来自于文献[14]，每个需求点的年度需求量的数值为随机生成，取值范围为0.2千吨到5千吨，需求量数据如表2所示。本文是在Windows10系统下进行的求解操作，模型采用CPLEX 12.80来进行求解，算法使用的是MATLAB 2018a软件来进行编写。遗传算法的种群规模为300，迭代次数为500，交叉概率为0.9，变异概率为0.1，精英保留比例为0.3。其他相关参数如表3所示。

表2 各需求点的需求量数据

表3 其他相关参数

3.2 算例求解

采用传统的遗传算法与本文改进之后的遗传算法分别求解单目标下的时间满意度的最大值，两种算法的求解次数均为10次，取10次中的最优结果作为最终时间满意度的最大值，两种算法的优化过程如图4所示，通过对比可以发现本文改进后的遗传算法的寻优能力与收敛速度均优于传统的遗传算法。

图4 改进遗传算法的时间满意度迭代过程

通过K-means聚类算法将130个需求点聚成11类，得到11个聚类中心，聚类结果如图5所示。

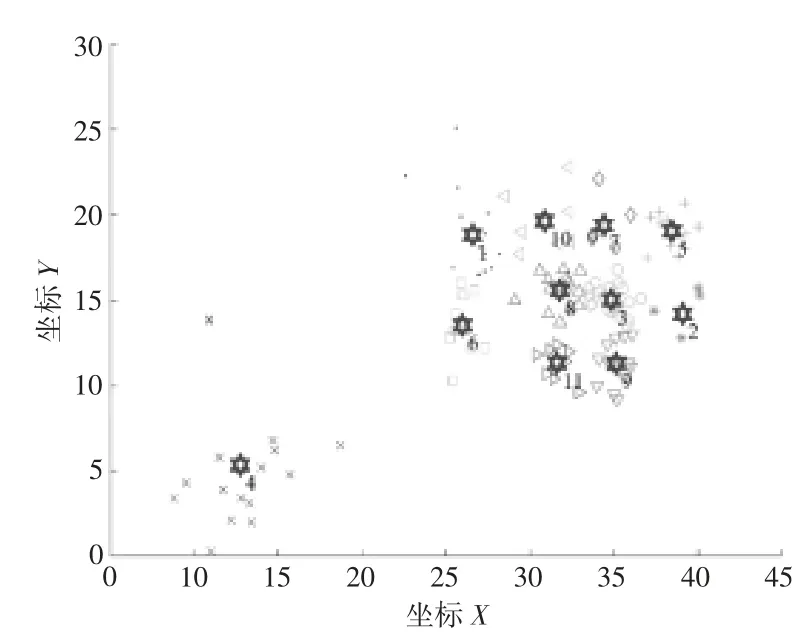
图5 需求点聚类结果

运用CPLEX对模型进行求解，最终从11个聚类中心中选出聚类中心1、3、4、5、6、8、9作为前置仓建设点，最终前置仓覆盖结果如图6所示。运用改进之后的遗传算法对模型进行求解，得到将需求点17、26、47、61、72、102、117作为前置仓建设点，最终前置仓覆盖结果如图7所示。

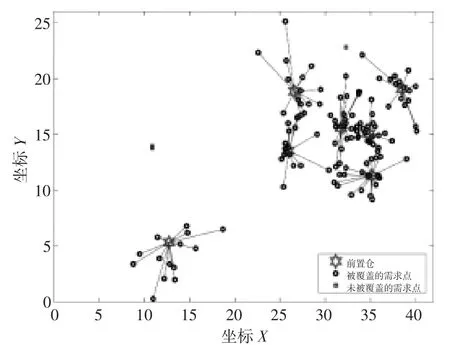
图6 运用CPLEX模型求解前置仓覆盖结果

图7 运用改进后的遗传算法模型求解前置仓覆盖结果

3.3 结果分析

根据上述所给参数，分别计算出CPLEX软件与改进之后的遗传算法（下文简称“GA”）在两个目标函数各自为单目标函数情况下的极值，求解结果如表4所示。

表4 单目标求解结果

将计算出的数值带入公式（6）中，ω的取值为0.1～0.9，取值间隔为0.1，CPLEX与GA的计算结果见表5所示。

表5中CPLEX的求解结果均为双目标优化的帕累托最优解，决策者可根据自身的偏好，选择相应的最优解。本文选取ω=0.4、0.6时，成本为171.8327万元，时间满意度为240.2521作为CPLEX的最终求解结果。在GA的求解结果中，当ω=0.5时的结果要优于ω=0.4、0.6、0.7时的求解结果，所以ω=0.4、0.6、0.7时的解为劣解，应予以淘汰，本文选取ω=0.5时，成本为167.9798万元，时间满意度为227.2361作为GA的最终求解结果。

表5 不同ω取值下CPLEX与GA的计算结果

在ω相同的条件下，将CPLEX与GA计算出的成本与时间满意度的结果进行对比，除了ω的取值为0.5和0.6的情况下，CPLEX求出的成本不仅比GA小，并且时间满意度还比GA大，求解结果完全优于GA。在ω=0.5和0.6时，虽然CPLEX所计算出的成本与时间满意度均高于GA，但仔细比较来看，在成本上CPLEX与GA的成本差异幅度较小，在时间满意度上CPLEX与GA差异的幅度要高于成本的差异幅度，说明CPLEX求解的将聚类中心作为候选点的选址方案成本效用更高。综上分析，将聚类中心作为候选点的选址效果要优于将需求点作为候选点的选址效果。

4 结束语

本文针对前置仓选址问题，在分析现有物流配送中心选址模型的特点和不足的基础上，从满足顾客时间需求的角度来考虑前置仓选址问题，引入了时间满意度这一概念，建立了以总配送成本最小，总顾客需求点的时间满意度最大的双目标选址模型。在传统的遗传算法之上引入了精英保留策略并基于进化逆转的思想提出了进化突变操作，并用算法对模型进行了求解，从理论和具体实施两个层面分析了所建模型及算法的有效性。通过对比两种候选点选取方式的最终求解结果，发现以聚类中心作为候选点的方式要优于将需求点本身作为候选点的方式。现有关于物流配送中心选址和前置仓选址研究较少考虑时间满意度因素和不同候选点选取方式的优劣性，本文在一定程度上丰富了相关的设施选址理论及应用，为前置仓选址布局提供了决策参考。