组态思维视角下物流效率的建设路径研究

0 引言

自2009年颁布《物流业调整和振兴规划》以来，物流业成为了我国的支柱性产业之一。自此之后，“物流效率”的概念开始明确并逐步成为实现复兴工作的抓手。例如《国家物流枢纽布局和建设规划》（以下简称《规划》）中指出，将建设一批能够使得物流运行效率大幅提高的国家物流枢纽。然而如何能够有效提高物流效率发展，是否存在着高质量发展路径，目前尚未出现一个宏观的研究进行讨论。

“物流效率”的研究目前已形成了较为固定的研究范式。学者们普遍选取合适的指标及案例，通过数据包络分析（Data Envelopment Analysis，DEA）测算效率。本文试图在其基础上与组态理论结合，该理论认为“事物的发生是不同条件组合影响的结果”，考虑了因素之间的复杂组合机制，能够进一步剖析效率建设过程中的组态发展路径[1]。

基于此，本文使用定性比较分析（Qualitative Comparative Analysis,QCA）与DEA相结合展开研究。首先通过DEA测算我国各省的物流效率，进而以必要条件分析（Necessary Condition Analysis，NCA）充分讨论各因素对结果的必要性程度，最后通过QCA开展组态分析，挖掘我国物流效率建设背后的组态构型。本研究在以往物流效率相关研究的基础上进一步结合组态理论，摒弃了传统对单一因素的讨论[2]，而是考虑了因果复杂性问题，主要解答了以下问题：我国物流效率建设过程中是否存在必要条件？是否存在高质量路径？

1 研究方法与设计

1.1 案例选择与数据来源

本文将我国30个省、市、自治区作为研究案例。由于西藏的官方数据并未实时更新，因此本文暂不考虑。考虑到2021年各地的统计数据尚未完全更新，本文最终选取2014—2020年各地运输、仓储、邮政等行业的数据作为本文原始数据，数据均来自《中国统计年鉴》。

1.2 研究方法与变量选取

DEA是一种能够测算物流效率并评价有效性的决策方法。DEA以相对效率为基础，构建多投入和多产出指标体系，利用数学规划模型对同类型决策单元进行有效性测算，为了考虑时间因素，本文使用DEA-Malmquist指数[3]。以往DEA研究中普遍将人力、固定资产等变量作为投入，总值、货运量作为产出。本文最终选择物流从业人员工资、固定资产投入、物流土地投入作为投入指标，从业人员数量、货运量及周转量作为产出指标进行DEA计算。

QCA基于组态思维，能够深度剖析某种结果出现时的因素组合[4]。而为了进一步剖析物流效率建设过程中的高质量发展路径，本文将DEA计算所得的生产率作为结果变量。条件变量的获取本文基于文献归纳法，扎根于各类物流宏观政策，最终选择了经济、交通、人口、科技、开放五种条件变量。最终的物流效率组态评价体系如表1所示。

表1 物流效率组态评价指标

1.3 数据分布与模糊校准

QCA研究中的模糊集相较于其他方法，需要开展模糊校准，延伸了对数据的处理方式，本文选择模糊集开展研究。在校准前首先需要了解数据的分布情况，进而选择合适的校准锚点。描述性统计分析完成后，本文最终选择了上下四分位点以及中位数分别作为完全隶属、完全不隶属、交叉点的校准锚点[5]。描述性统计结果及校准锚点如表2所示。

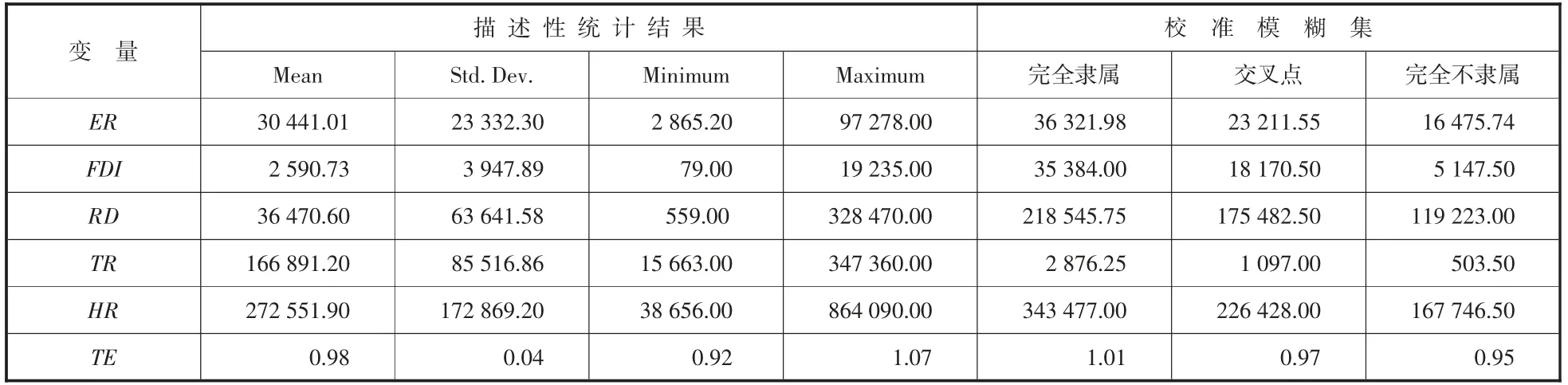
表2 描述性统计及校准锚点

2 实证与分析结果

2.1 全要素生产率结果

本文使用Deap2.1对30个案例省（市）的物流业效率进行测算，结果如表3所示。由表3可知，不同区域的物流业全要素生产率存在较大差异，北京、江苏等10个地区的全要素生产率指数大于1，其余地区均小于1。为了探究地区发展差异，并找到物流效率背后的发展组合，本文在DEA基础上进一步使用QCA开展分析。

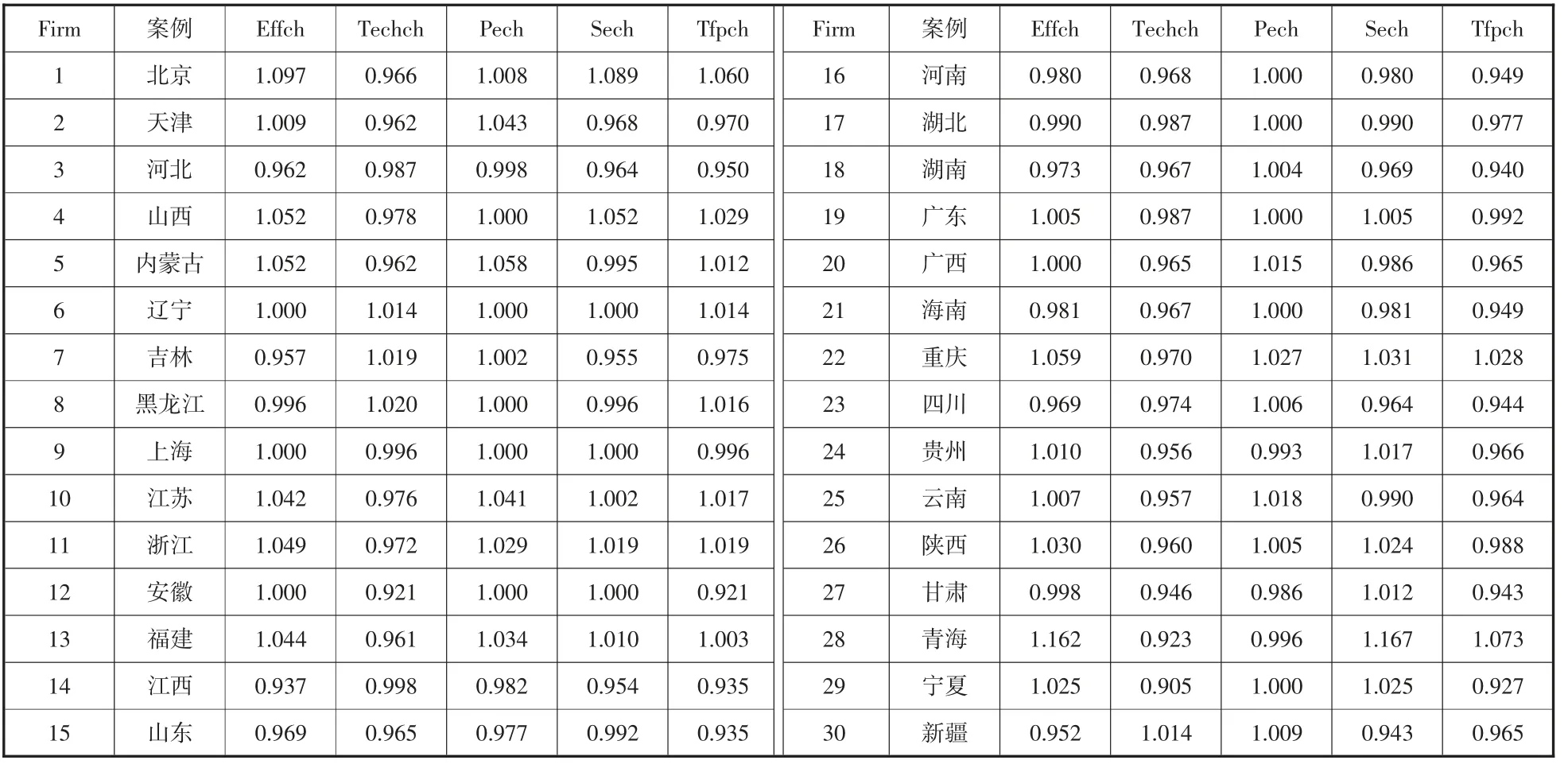
表3 2014—2020年各省（市）物流业全要素生产率

2.2 QCA与NCA必要性分析

在进行组态分析前首先需要开展必要性测试，用以判断某一条件是否构成结果的必要条件。当某条件与结果一致性达到0.9时，即认为该条件为必要条件，且在组态分析中也将作为核心条件出现。如表4所示，各条件均未达到0.9，并未直接构成必要条件。

表4 物流效率QCA必要性检测

而为了进一步判断各条件对结果的必要性程度，本文以NCA中的效应值进一步研究。该方法能对单一条件的必要性细粒度展开更深入的讨论，是QCA必要性分析的良好补充[6]。从效应值(d)来说，0＜d＜0.1时表示效应值较小，0.1≤d＜0.3时表示效应值中等，0.3≤d＜0.5时表示效应值较大，d≥0.5时表示效应值非常大。当效应值大于0.1且蒙特卡洛仿真置换检验（Monte Carlo Simulations of Permutation Tests）显示效应量显著时可认为某条件构成结果的必要条件。从表5中看出，各条件效应值均未达到必要条件水平，与QCA结果一致，即并不存在能直接影响物流效率建设的关键因素。

表5 NCA效应值与显著性结果

2.3 组态分析

QCA的组态分析中将形成三种解，中间解相较于复杂解与简约解考虑了价值较高的逻辑余项，因此本文汇报中间解。考虑到本文的案例数为30，属于中小样本研究，因此本文将案例阈值设为1，一致性阈值为0.8，PRI一致性默认。并且由于必要条件分析中并未检测出核心条件，本文将以另一种方式识别构型中的核心因素：当某条件同时出现在相对应的中间解和简约解时为核心条件，仅出现在中间解时为边缘条件。如表6为最终的中间解组态构型。其中一致性代表着构型与结果的相似度，覆盖度代表对结果变量的解释程度。

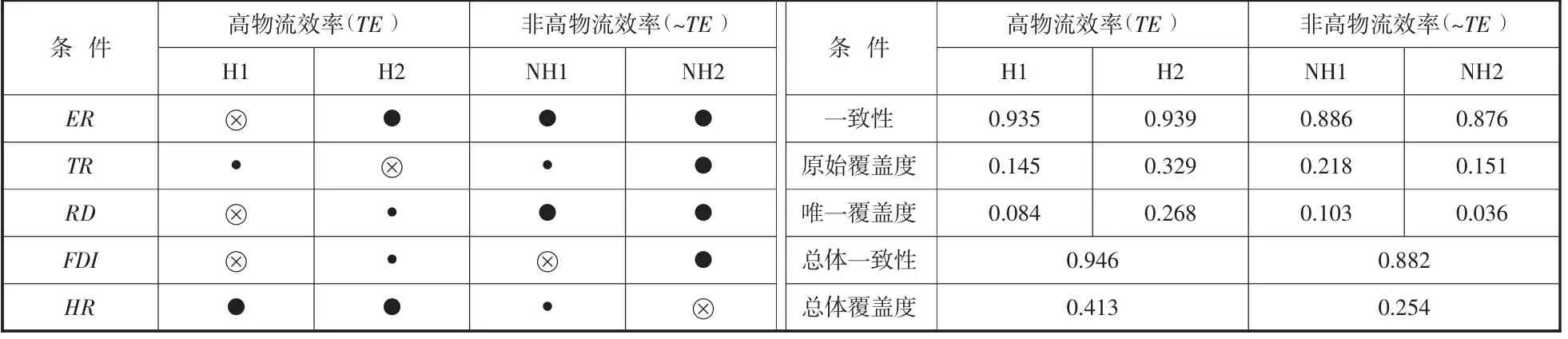
表6 物流效率高与非高时的组态构型

人力驱动型。该路径意味着非高ER、非高RD、非高FDI、高HR作为核心条件，高交通环境为边缘条件可以导致高物流效率的产生。黑龙江是该路径下的典型省份。可以看到，该路径虽然与高效率的一致性达到了0.935，但覆盖率较低。

人力与经济双元驱动型。该路径意味着高ER、高HR、非高TR为核心条件，高RD、高FDI作为边缘条件的条件组合可以导致高物流效率的产生。处于该路径下的省市为：北京、上海、浙江、福建、辽宁。该路径与人力驱动型相比，一致性相似，但覆盖度更高，且处于该路径下的案例更多，属于结构更为成熟的组态构型。

经济与科技双元驱动型。该路径意味着高ER、高RD、非高FDI为核心条件，高TR、高HR为边缘条件的条件组合会导致非高物流效率的产生。河南与河北是处于该路径下的典型案例。

多元因素驱动型。该路径意味着高ER、高TR、高FDI、高RD、非高HR均作为核心条件出现的条件组合会导致非高物流效率的产生。湖南是处于该路径下的唯一案例，虽然该路径的一致性较高，但解释力度相较于前一条路径并不大。

3 结论与讨论

3.1 研究结论

本文使用DEA-Malmquist指数测算2014—2020年30个省、市、自治区的物流效率，并对全要素生产率进行关键因素的识别以及组态构型分析。结果显示：（1）能够直接影响物流效率建设的关键因素并不存在，但人力资源相较于其他因素，在必要性测试中更为突出，且在两条高物流效率的发展路径中均以核心条件出现；（2）出现了两条高物流效率的发展路径，分别是以黑龙江为典型案例的人力驱动型以及以北京、上海等地为案例的人力与经济双元驱动型路径；（3）出现了两条非高物流效率的路径，分别是以河南、河北为典型案例的经济与科技双元驱动型路径以及一条以湖南为案例的多元因素驱动型路径。

3.2 贡献与管理启示

本文的贡献主要在于：第一，在以往使用DEA作为研究工具的物流研究基础上，使用组态理论，进一步挖掘背后的优质发展路径，提供了较新的研究视角。第二，以QCA+NCA的形式展开因素的必要性讨论，这种方法的应用在物流领域较为新颖。

本文基于研究结论总结了如下的管理启示。（1）聚焦物流人才以及人力的投入。通过QCA+NCA的双重识别发现，人力资源虽然并未直接构成高物流效率的必要条件，但在两条高效率建设的构型中均作为核心条件存在。因此在组态视角下，人力是更为突出的关键因素。（2）注重组态思维发展。通过DEA+QCA本文挖掘出两条高物流效率的发展路径，其中以北京、上海为案例的路径在解的一致性与解释力度方面均十分强，且两条发展路径在稳健性测试后仍保持稳定。（3）规避发展误区，注重对标发展。本文同样发现了两条非高物流效率的路径，且有3个省份隶属于其中。本文建议这类地区以对标发展的思维将本文两条高物流效率发展路径作为对标路径，查漏补缺，针对性发展。

3.3 不足与展望

本文扩充了现有的研究，提供了较新的研究方法，但本文仍存在一定缺憾，以待未来进一步研究。第一，未来可通过改变投入产出指标或是QCA变量来开展更为细致的研究。第二，未来可以考虑将多个年份的物流效率结果均进行组态分析，以动态的目光审视发展路径。最后，未来可以采取大样本研究，以提高最终管理启示的普适性。