基于XFEM 和GA-BP 神经网络的裂纹智能识别研究*

毛晓敏， 张慧华， 纪晓磊， 韩尚宇

（南昌航空大学 土木建筑学院，南昌 330063）

引 言

随着建造水平及民众安全意识的不断提高，人们对实际工程结构的安全问题愈发重视.受不同因素的影响，在建造和使用过程中，结构中难免会产生各类缺陷（如裂纹、孔洞等）.裂纹这类代表性缺陷的存在会影响结构的承载力、适用性和耐久性，甚至可能会造成结构物的垮塌等严重事故.因此，及时发现结构中的裂纹是确保结构安全的关键措施之一.目前，较为常见的裂纹检测和识别方法主要包括人工检测、图像识别法和无损检测技术等，但这些方法存在着一些固有的局限，比如，人工检测费时费力、图像识别法易受环境影响、无损检测技术费用较为昂贵等.近年来，数值技术与人工智能算法的有机结合凭借其高效率、高精度、低成本和适用性强等特点在裂纹识别等反分析问题中得到了广泛的应用.

基于数值技术和人工智能算法建立的裂纹反演分析模型一般包括正向分析和目标极小化两个部分.正向分析通过各类数值方法获取含裂纹结构中测点的响应值（如位移）；目标极小化则利用相关智能优化算法对正向分析中的一系列输入和响应数据进行处理，据此进一步预测裂纹信息.早期，有限元法[1]和边界元法[2]被广泛地用于裂纹问题的正向分析，这两种数值方法均要求单元边与裂纹几何一致，这导致需要不断进行网格重构以获取不同裂纹形态下的测点响应，大大降低了计算效率.而扩展有限元法 (XFEM)[3]正好可以弥补上述不足，XFEM 通过引入非连续位移模式，可在网格固定的情况下改变水平集函数模拟域内不同构型（如不同的缺陷类型、位置、尺寸和数量等）的缺陷，大大降低了正向分析的成本.至今，XFEM 已被应用于求解诸多裂纹问题[4-5].在智能优化算法方面，人工蜂群 (ABC)算法[6]、遗传算法 (GA)[7]和各类人工神经网络算法（如误差反向传播多层前馈（BP）神经网络[8]）等是其中的典型代表.

国内外已有不少学者结合XFEM 与智能优化算法进行了缺陷反演.文献[9]基于XFEM 和改进ABC 算法对结构内部单个圆形、椭圆形缺陷和两个不规则缺陷进行了反演分析.文献[10]提出了一种基于动态XFEM 和改进ABC 的多缺陷检测法.为准确检测和识别结构中的裂纹，文献[11]发展了一种基于XFEM 和GA 的计算工具，文献[12]阐述了XFEM 和GA 在结构缺陷检测中的实验应用与改进，文献[13]建立了XFEM与GA 相结合的缺陷反演分析模型.

GA 是一种全局性概率搜索方法[14]，该算法独立于求解域且具有较强的鲁棒性，但其存在收敛速度慢和局部搜索能力差等问题.作为当前应用最为广泛的神经网络模型之一，BP 神经网络具有较强的局部搜索能力，可有效弥补GA 的缺点.与此同时，GA 的全局随机搜索能力也可防止BP 神经网络陷入局部最优，即GA 和BP 可以实现互补.基于GA-BP 开展的研究已有不少[15-16]，但利用XFEM 和GA-BP 神经网络进行缺陷识别的相关研究工作尚未见报道.为此，本文将XFEM 与GA-BP 神经网络算法进行有机结合，采用XFEM 获得GABP 神经网络的训练数据，利用GA 对BP 神经网络的初始权值和阈值进行优化，围绕线弹性断裂力学中的理想化直线裂纹进行反演分析.通过典型算例验证模型的可行性和精度，并进一步探讨输入数据噪声对网络预测结果的影响，为结构中裂纹的快速准确识别提供初步的理论和技术支撑.

1 裂纹反演模型简介

进行裂纹识别时，一般先通过计算模拟或实验器材检测获得结构中某些关键点（即测点）的位移等响应量，在此基础上运用相关方法来反演结构中裂纹的几何信息.以图1 给出的双直线裂纹识别问题为例，待反演的参数向量为

图1 含裂纹结构及测点示意图Fig. 1 Schematic diagram of the structure with cracks and the measuring points

2 XFEM 简介

2.1 裂纹问题的XFEM 位移近似函数

XFEM 是在单位分解法[18]和标准有限元法的基础上发展起来的新型数值方法.通过在标准有限元逼近函数中引入裂面改进函数和裂尖改进函数，XFEM 可在与裂纹几何不一致的稀疏网格上获得高精度的解答.以各向同性材料中的裂纹问题为例，XFEM 的位移近似函数可表示为[18]

2.2 XFEM 离散方程

基于已构造的位移近似(式(5))，进一步根据变分原理可导出XFEM 求解裂纹问题的总体离散方程为[19]

3 GA-BP 神经网络算法

BP 神经网络是一种信号前向传播、误差反向传递的多层前馈网络[8].它主要由一个输入层、一个或多个隐藏层以及一个输出层构成.BP 神经网络是目前应用最广泛的神经网络模型之一、具有较强的非线性映射能力、自学习和自适应能力、泛化能力以及容错能力，主要缺点则包括易陷入局部极小化、收敛速度较慢以及网络结构选择不一等[20].GA 是一种全局随机搜索优化计算技术[21]，其基本原理可以总结为“优胜劣汰”四个字，主要优点有：①适用于复杂的优化问题且可获取优化问题的全局最优解；②算法独立于求解域；③具有较强的鲁棒性；其不足之处主要表现在收敛速度慢、局部搜索能力差和需要控制的变量多.

为了提高BP 网络的收敛速度和降低陷入局部最优的可能性，本文采用GA 对BP 神经网络的初始权值和阈值进行优化，算法的总体实现框架见图2.

图2 GA 优化BP 神经网络的流程图Fig. 2 The flow chart of the BP neural network optimized by GA

3.1 确定BP 神经网络的结构

3.2 基于GA 对BP 神经网络的初始权值和阈值进行优化

基于GA 优化BP 神经网络的具体计算过程为[20]：

① 初始值编码.首先采用实数编码法对BP 神经网络的初始权值和阈值进行编码，个体编码的长度计算公式为

② 确定适应度函数.采用BP 神经网络的训练输出值与期望输出值误差平方和的倒数作为个体i的适应度函数Fi，即

图3 BP 神经网络的结构模型Fig. 3 The structure of the BP neural network

按照所选择的适应度函数并通过遗传中的选择、交叉和变异对个体进行筛选，使适应度好的个体保留下来.通过反复循环，将种群中最终得到的最优个体作为BP 神经网络的最优权值和阈值.

3.3 计算BP 网络的训练误差

将GA 算法得到的最优个体赋值为BP 神经网络的初始权值和阈值，利用训练样本对网络进行训练，其中隐藏层和输出层的输出计算分别为

3.4 判断迭代是否结束

判断式(20)得到的误差是否满足精度要求.若满足，则网络迭代结束，据此可开展裂纹识别；若不满足，可参考文献[20]对权值和阈值进行更新，并通过式(18)～(20)重新计算网络的训练误差，如此循环直至满足精度要求.

4 XFEM 与GA-BP 神经网络的实现

本文运用XFEM 与GA-BP 神经网络算法进行裂纹反演分析.该方法主要包括两部分：一部分是运用XFEM 进行正向分析以获取测点的位移响应量，另一部分则是利用测点位移数据对GA-BP 神经网络进行训练并据此识别裂纹几何参数.方法的主要实现流程如图4 所示.

图4 XFEM 与GA-BP 神经网络算法开展裂纹识别的流程图Fig. 4 The flow chart of crack identification based on the XFEM and the GA-BP neural network algorithm

5 算 例 分 析

5.1 矩形板内的单边水平裂纹识别

如图5 所示，矩形板高H=6 m ， 宽W=2 m， 板左侧在距板上边缘H/2处 有一长度为a的单边水平裂纹.板顶部受到 σ =1 MPa 的 拉应力作用，板底边的竖向位移和底边左端的水平位移均为零.弹性模量E=2.1×1011Pa，Poisson 比ν =0.3， 按平面应变进行分析.式(20)中的误差ek取为10-7.

图5 单向拉伸作用下含单边裂纹的矩形板Fig. 5 A rectangular plate with an edge crack under uniaxial tension

5.1.1 XFEM 精度验证

通过校核应力强度因子的求解精度来测试XFEM 的正向分析精度.分别基于4 种由四结点矩形单元组成的网格对a=0.7 m 的裂纹进行模拟（单元数量分别为120，435，780 和1 540，相应的离散域见图6）.表1 给出了裂尖A 的XFEM 仿真结果及相应的参考解[23]，括号内是相对误差，可以看出随着网格的加密，XFEM 解逐渐趋于参考解，很好地展示了该方法的收敛性.

图6 XFEM 网格：(a) 120 个单元； (b) 435 个单元； (c) 780 个单元； (d) 1 540 个单元Fig. 6 XFEM meshes: (a) 120 elements; (b) 435 elements; (c) 780 elements; (d) 1 540 elements

表1 不同网格下的 KI(单位：MPa·m1/2)Table 1 K I for different meshes (unit: MPa·m1/2)

5.1.2 GA-BP 神经网络的训练和预测结果

1) 网络的训练

网络的输入数据为XFEM 模拟得到的测点位移值，输出数据为裂尖A 的X坐标（即XA）.XFEM 仿真时采用图6(c)的网格对裂纹长度取0.5 m，0.6 m，0.7 m，···，1.4 m 等10 种情况进行模拟.首先按图7(a)的方式布置14 个测点，各测点的坐标值列于表2.据此，BP 神经网络的输入层、隐藏层和输出层的神经元个数分别取为14，4 和1；此外，GA 中种群的最大迭代次数为50，种群规模为20，种群的交叉概率为0.5，变异概率为0.1.为验证GA-BP 神经网络的可靠性，采用训练数据进行裂尖坐标预测，相关结果见表3，可以看出，对给定的10 种裂纹构型，该网络的预测精度都很高.

表2 测点坐标Table 2 Coordinates of measuring points

表3 GA-BP 神经网络对XA 的训练输出结果Table 3 Training results of the GA-BP neural network for XA

2) 网络的预测精度

裂纹长度先后取0.5 m，0.6 m，0.7 m，···，1.4 m，1.5 m 等11 种情况，对每种情形，分别基于XFEM 并按图7所示的6 种测点布置方案获取对应的位移值.网络搭建时，采用a=0.5 m，0.6 m，0.7 m，···，1.4 m 等10 种情形对应的结果作为训练数据，并分别基于搭建好的GA-BP 神经网络和传统BP 神经网络模型（神经网络的结构相同）预测裂尖的坐标值，即将a=1.5 m 时的测点位移值作为网络的输入数据以预测XA.相关结果列于表4.可以看出，GA-BP 神经网络预测的最大相对误差为2.16%，而传统BP 神经网络预测的最大相对误差为6.51%，且同等情况下GA-BP 神经网络模型的预测精度大体上高于传统BP 神经网络，很好地展示了本文方法的优越性.此外，从表4 还可以看出，在6 个测点布置方案中，传统BP 神经网络预测时方案2 的效果最佳，而GA-BP 神经网络预测时方案3 和方案5 的效果最佳.在GA-BP 神经网络预测的情况下，可发现方案1 胜于方案2，方案3 胜于方案4，方案5 胜于方案6，由此可见，矩形板上边缘的测点有利于结构内部裂纹的检测识别，这主要是因为板顶部距有位移约束的板底较远，其上各点的变形对裂纹构型变化的敏感度更大.

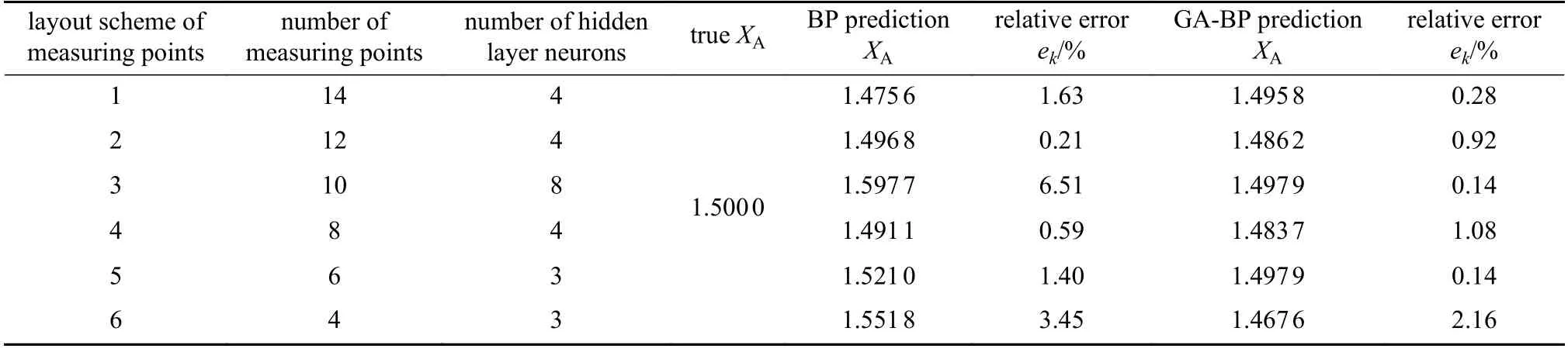
表4 BP 与GA-BP 神经网络预测的XA 值Table 4 Prediction of XA by BP and GA-BP neural networks

为了测试GA-BP 神经网络的稳定性，进一步对由XFEM 模拟获得的输入数据添加噪声，即

其中，uinput为 GA-BP 神经网络的输入数据（即输入的测点位移值），uXFEM为XFEM 正向分析获得的测点位移值， δ为噪声的大小（百分比）.

图8 给出了 δ分别取1%，2%，5%和10%时XA预测的相对误差绝对值随噪声值的变化情况（测点按图7方案5 布置，隐藏层神经元数量取3）.可以看出，随着噪声值的增加，裂尖位置预测的相对误差逐渐增大.此外，还可发现当噪声强度等级不超过10%时，XA预测的相对误差均小于1%，表明搭建的GA-BP 神经网络具有较好的容噪性和鲁棒性.

图7 测点布置方案：(a) 方案1，14 个测点； (b) 方案2，12 个测点； (c) 方案3，10 个测点；(d) 方案4，8 个测点；(e) 方案5，6 个测点； (f) 方案6，4 个测点Fig. 7 Layouts of measuring points: (a) scheme 1, 14 points; (b) scheme 2, 12 points; (c) scheme 3, 10 points;(d) scheme 4, 8 points; (e) scheme 5, 6 points; (f) scheme 6, 4 points

图8 不同噪声下XA 预测的相对误差绝对值Fig. 8 Absolute values of relative errors of predicted XA under various noises

5.2 方板中的内嵌双斜裂纹识别

如图9 所示，方板边长L=2 m，两条裂纹的长度均为a（单位 m），裂纹与水平方向夹角均为 β =45°，裂纹中心点至板左右两侧的距离b=0.7 m，其他条件与5.1 小节相同.

图9 单向拉伸荷载作用下含双斜裂纹的方板Fig. 9 A square plate with two inclined cracks under uniaxial tension

5.2.1 GA-BP 神经网络的训练和预测结果

1) 网络的训练

网络的输入数据仍采用XFEM 模拟得到的测点位移值，输出数据为裂尖A、B、C、D 的坐标，即(XA,YA)、(XB,YB)、(XC,YC)和(XD,YD).XFEM 仿真时采用图10 的网格，裂纹长度先后取0.500 m，0.528 m，0.556 m，0.585 m，0.613 m，0.641 m，0.670 m 和0.698 m，12 个测点的布置如图10 所示.据此，BP 神经网络的输入层、隐藏层和输出层的神经元个数分别取为12，4 和4；GA 中种群的最大迭代次数为50，种群规模为20，种群的交叉概率为0.5，变异概率为0.1.为验证网络的可靠性，采用训练数据进行裂尖坐标预测，相关结果见表5 ～ 8.可以看出，对给定的8 种裂纹尺寸，该网络的预测精度都很高.

表5 GA-BP 神经网络对裂尖A 坐标的训练值Table 5 Training coordinates of crack tip A by the GA-BP neural network

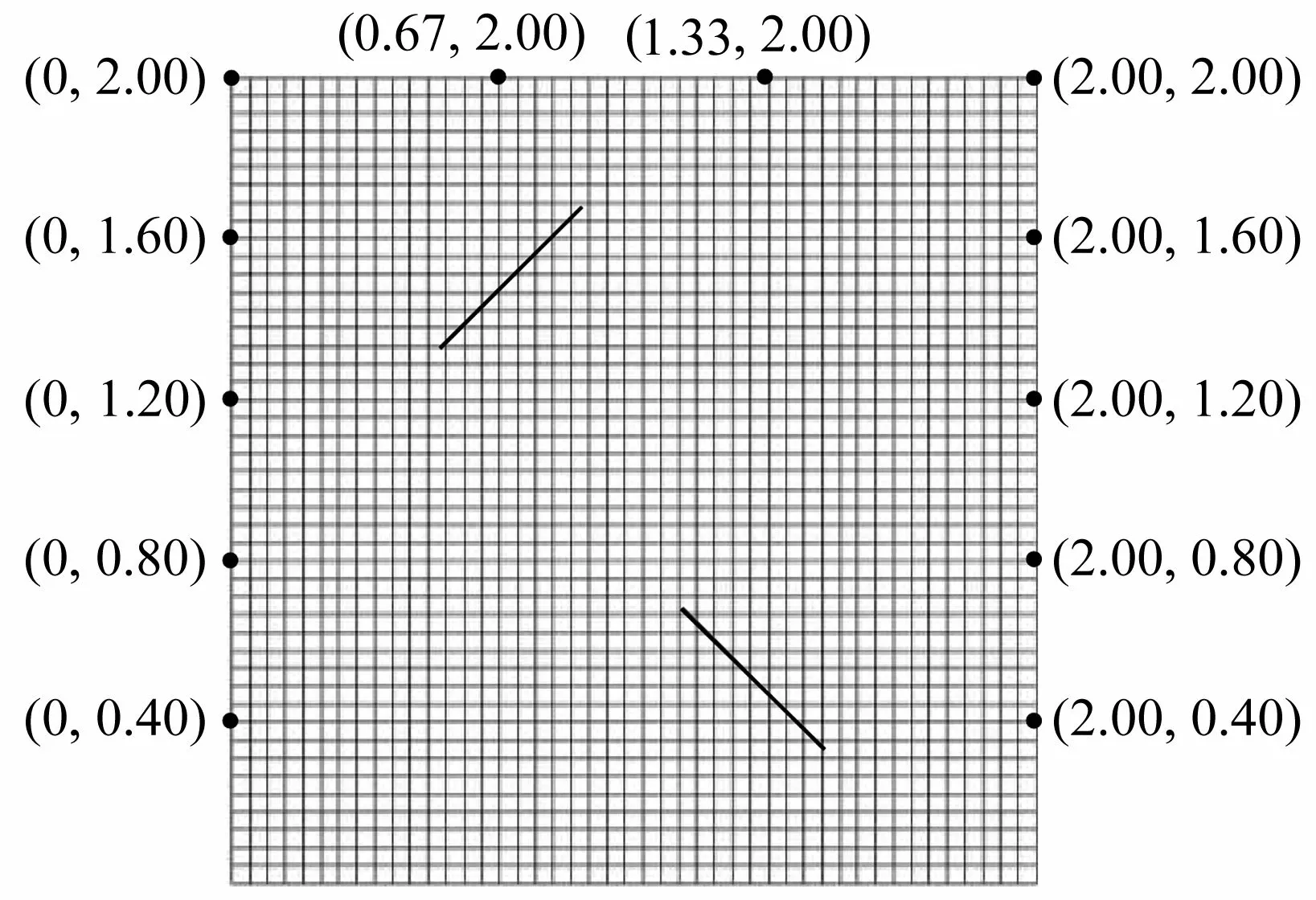
图10 XFEM 网格和测点布置 (a=0.5 m)Fig. 10 The XFEM mesh and measuring points (a=0.5 m)

2) 网络的预测精度

基于已经搭建好的GA-BP 神经网络和传统BP 神经网络，将a=0.726 m，0.755 m 和0.783 m 时由XFEM得到的测点位移作为输入数据，分别预测各裂尖的坐标值，相应的结果见表9 和10.可以看出，除个别情况（a=0.783 m 时的YC）传统BP 神经网络的预测精度稍高外，GA-BP 神经网络的预测结果与实际值均更吻合，可见本文搭建的GA-BP 神经网络较传统的BP 神经网络总体上拟合度更高、误差更小、更有利于结构内部裂纹的定位识别.

表6 GA-BP 神经网络对裂尖B 坐标的训练值Table 6 Training coordinates of crack tip B by the GA-BP neural network

表7 GA-BP 神经网络对裂尖C 坐标的训练值Table 7 Training coordinates of crack tip C by the GA-BP neural network

表8 GA-BP 神经网络对裂尖D 坐标的训练值Table 8 Training coordinates of crack tip D by the GA-BP neural network

表9 BP 与GA-BP 神经网络对裂尖A、B 的预测值Table 9 Prediction of crack tips A and B by BP and GA-BP neural networks

表10 BP 与GA-BP 神经网络对裂尖C、D 的预测值Table 10 Prediction of crack tips C and D by BP and GA-BP neural networks

为进一步测试网络的鲁棒性，仍然对输入数据添加噪声.真实裂纹长度依次取0.726 m，0.755 m 和0.783 m，图11 和12 给出了噪声值依次取1%，2%，5%和10%时4 个裂尖坐标相对误差的绝对值.可以看出，随着噪声强度等级的增加网络预测的相对误差也逐渐增大.此外，在同一裂纹长度和同一噪声值下，裂尖A 的误差大都大于裂尖B，XC的误差也基本大于XD，而YC的误差则小于YD.当噪声强度不超过5%时，预测结果的误差均在10%以内且绝大部分小于5%，当噪声强度为10%时，绝大部分误差在8%以内，表明搭建的网络具有较好的鲁棒性.此外，由图12 可以看出，对于三种裂纹长度，YD的预测误差均明显大于其他情况，这主要与裂尖D 的位置和测点分布有关，由于该裂尖靠近板底部，而板底部所有点的Y向位移均为零，致使该裂尖附近区域点（含部分测点）的纵向位移对外载和裂纹长度变化的响应不明显，从而导致预测精度的退化.此外，还可以看出4 个裂尖的X坐标的预测精度总体较Y坐标的更高，这主要与整块板仅左下角点处存在水平位移约束有关；而对裂尖D，由于其距水平约束点最远，相较于其他裂尖，D 点附近区域点的水平位移受该约束的影响最小，进而使得相关的响应对裂纹构型的变化更敏感，因而XD的预测精度整体来说较其他裂尖的对应值更高.

图11 不同噪声下，XA，XB，XC 和XD 预测值的相对误差绝对值Fig. 11 Absolute values of relative errors of predicted XA, XB, XC and XD under different noises

图12 不同噪声下，YA，YB，YC 和YD 预测值的相对误差绝对值Fig. 12 Absolute values of relative errors of predicted YA, YB, YC and YD under different noises

6 结 论

通过在标准有限元的框架内引入裂面和裂尖改进函数，XFEM 可使用固定网格对不断变化的裂纹构型进行高精度模拟.GA 是一种独立于求解域且具有较强鲁棒性的全局性概率搜索方法，BP 神经网络优化算法则具有较强的非线性映射能力和局部搜索能力.本文结合了三者的优点，基于XFEM 获取网络训练数据，利用GA 对BP 神经网络的初始权值和阈值进行优化，建立了用于结构内部直线裂纹反演分析的XFEM 与GABP 神经网络方法.在给出XFEM、GA 和BP 神经网络基本原理的基础上，重点阐述了GA 优化BP 的结合策略和计算过程，最后通过两个典型算例对其精度和鲁棒性等进行了验证，并探讨了网格密度、测点布置和输入数据噪声等因素对精度的影响.结果表明，XFEM 正向分析的精度、GA-BP 神经网络的裂纹识别精度及鲁棒性均较好.另外，与传统的BP 神经网络对比，本文搭建的GA-BP 神经网络的预测精度普遍更高.

需要说明的是，本文基于经典的线弹性断裂力学模型开展分析，选用了较简单的裂纹构型（如单直线和双直线裂纹等）进行反演分析.但就方法本身而言，本文的工作可以推广至更复杂的如多裂纹、分支、交叉和曲线裂纹等的预测工作中.在现有工作的基础上，后期我们将进一步围绕更复杂更贴合实际的裂纹开展更深入的研究工作.

参考文献（ References ） ：

［1］KWAN A K H, MA F J. Crack width analysis of reinforced concrete under direct tension by finite element method and crack queuing algorithm[J].Engineering Structures, 2016, 126（1）: 618-627.

［2］XIE G Z, ZHOU F L, LI H, et al. A family of non-conforming crack front elements of quadrilateral and triangular types for 3D crack problems using the boundary element method[J].Frontiers of Mechanical Engineering,2019, 14（3）: 332-341.

［3］ 李录贤, 王铁军. 扩展有限元法(XFEM)及其应用[J]. 力学进展, 2005, 35（1）: 5-20. （LI Luxian, WANG Tiejun. The extended finite element method and its application: a review[J].Advances in Mechanics, 2005, 35（1）: 5-20.（in Chinese））

［4］ 王振, 余天堂. 模拟三维裂纹问题的自适应多尺度扩展有限元法[J]. 工程力学, 2016, 33（1）: 32-38. （WANG Zhen,YU Tiantang. Adaptive multiscale extended finite element method for simulating three-dimensional crack problems[J].Engineering Mechanics, 2016, 33（1）: 32-38.（in Chinese））

［5］XIAO G Z, WEN L F, TIAN R. Arbitrary 3D crack propagation with improved XFEM: accurate and efficient crack geometries[J].Computer Methods in Applied Mechanics and Engineering, 2021, 377: 113659.

［6］LI Y M, XIA Y D, XIE D L, et al. Application of artificial bee colony algorithm for particle size distribution measurement of suspended sediment based on focused ultrasonic sensor[J].Transactions of the Institute of Measurement and Control, 2021, 43（7）: 1680-1690.

［7］ALHADDAD W, HALABI Y, MEREE H, et al. Optimum design method for simplified model of outrigger and ladder systems in tall buildings using genetic algorithm[J].Structures, 2020, 28: 2467-2487.

［8］MOLDOVANU S, OBREJA C-D, BISWAS K C, et al. Towards accurate diagnosis of skin lesions using feedforward back propagation neural networks[J].Diagnostics(Basel), 2021, 11（6）: 936.

［9］ 王佳萍, 杜成斌, 王翔, 等. 基于XFEM和改进人工蜂群算法的结构内部缺陷反演[J]. 工程力学, 2019, 36（9）: 25-31.（WANG Jiaping, DU Chengbin, WANG Xiang, et al. Inverse analysis of internal defects in structures using extended finite element method and improved artificial bee colony algorithm[J].Engineering Mechanics, 2019,36（9）: 25-31.（in Chinese））

［10］DU C, ZHAO W, JIANG S, et al. Dynamic XFEM-based detection of multiple flaws using an improved artificial bee colony algorithm[J].Computer Methods in Applied Mechanics and Engineering, 2020, 365: 112995.

［11］RABINOVICH D, GIVOLI D, VIGDERGAUZ S. XFEM-based crack detection scheme using a genetic algorithm[J].International Journal for Numerical Methods in Engineering, 2007, 71（9）: 1051-1080.

［12］CHATZI E N, HIRIYUR B, WAISMAN H, et al. Experimental application and enhancement of the XFEM-GA algorithm for the detection of flaws in structures[J].Computers and Structures, 2010, 89（7）: 556-570.

［13］ 王佳萍, 杜成斌, 江守燕. 扩展有限元与遗传算法相结合的结构缺陷反演分析[J]. 力学与实践, 2017, 39（6）: 591-596.（WANG Jiaping, DU Chengbin, JIANG Shouyan. Analysis of structural defect inversion based on extended finite element and genetic algorithm[J].Mechanics in Engineering, 2017, 39（6）: 591-596.（in Chinese））

［14］ 孟建军, 孟高阳, 李德仓. 基于SA-GA混合算法的动车组车辆轮重分配优化[J]. 应用数学和力学, 2021, 42（4）: 363-372. （MENG Jianjun, MENG Gaoyang, LI Decang. Optimization of wheel weight distribution for EMU vehicles based on the SA-GA hybrid algorithm[J].Applied Mathematics and Mechanics, 2021, 42（4）: 363-372.（in Chinese））

［15］WANG H Y, ZHANG Z X, LIU L M. Prediction and fitting of weld morphology of Al alloy-CFRP welding-rivet hybrid bonding joint based on GA-BP neural network[J].Journal of Manufacturing Processes, 2021, 63: 109-120.

［16］WANG Z W, FEI Y, YE P X, et al. Crack characterization in ferromagnetic steels by pulsed eddy current technique based on GA-BP neural network model[J].Journal of Magnetism and Magnetic Materials, 2020, 500:166412.

［17］ 江守燕, 杜成斌. 基于扩展有限元的结构内部缺陷(夹杂)的反演分析模型[J]. 力学学报, 2015, 47（6）: 1037-1045. （JIANG Shouyan, DU Chengbin. Numerical model for identification of internal defect or inclusion based on extended finite elememt methods[J].Chinese Journal of Theoretical and Applied Mechanics, 2015, 47（6）: 1037-1045.（in Chinese））

［18］ 张慧华. 典型不连续固体力学问题的数值求解[D]. 博士学位论文. 西安: 西安交通大学, 2009. （ZHANG Huihua.Numerical solutions to typical discontinuous problems in solid mechanics[D]. PhD Thesis. Xi’an: Xi’an Jiaotong University, 2009. （in Chinese））

［19］ 茹忠亮, 朱传锐, 张友良, 等. 断裂问题的扩展有限元法研究[J]. 岩土力学, 2011, 32（7）: 2171-2176. （RU Zhongliang, ZHU Chuanrui, ZHANG Youliang, et al. Study of fracture problem with extended finite element method[J].Rock and Soil Mechanics, 2011, 32（7）: 2171-2176.（in Chinese））

［20］ 冉雨晴, 吴玮, 狄鑫. 基于遗传算法优化BP神经网络的管网漏失定位模型研究[J]. 水电能源科学, 2021, 39（5）: 123-126. （RAN Yuqing, WU Wei, DI Xin. Study on leakage location model of water supply network based on bp neural network optimized by genetic algorithm[J].Water Resources and Power, 2021, 39（5）: 123-126.（in Chinese））

［21］HOLLAND J H.Adaptation in Natural and Artificial Systems: an Introductory Analysis With Applications to Biology, Control, and Artificial Intelligence[M]. Cambridge : The MIT Press, 1992.

［22］WANG X, AN S, XU Y Q, et al. A back propagation neural network model optimized by mind evolutionary algorithm for estimating Cd, Cr, and Pb concentrations in soils using vis-NIR diffuse reflectance spectroscopy[J].Applied Sciences, 2020, 10（1）: 51.

［23］ 中国航空研究院. 应力强度因子手册[M]. 增订版. 北京: 科学出版社, 1993. （Chinese Aeronautical Establishment.Stress Intensity Factor Manual[M]. revised and enlarged ed. Beijing: Science Press, 1993. （in Chinese））