计及多重阻塞的电动汽车移动储能特性建模*

严浩源， 赵天阳， 刘晓川， 丁肇豪

（1. 暨南大学 能源电力研究中心，广东 珠海 519070；2. 南洋理工大学 能源研究院，639798，新加坡；3. 华北电力大学 电气与电子工程学院，北京 102206）

引 言

电动汽车是减少交通系统碳排放、提高交通系统能源安全的主要途径之一.电动汽车也是新型电力系统的重要成员，其充电行为对电力系统安全、稳定、经济的负面影响已被广泛研究[1-2].通过有序放电，电动汽车具有规模化移动储能的属性，可有效支撑新型电力系统的低碳转型[3].相比于固定式储能，电动汽车的移动储能特性受道路可达性、充电设施阻塞等影响[4].因此，亟需开展低碳、多重阻塞环境下电动汽车移动储能特性的研究.

城市交通电力耦合系统(urban coupled transportation power systems，UCTPSs)由城市道路系统、充电设施和城市电网构成，提供交通、电力服务[5].在给定交通出行量及电力负荷需求的环境下，交通流、电力流在相关基础设施上聚合为交通电力流.为优化交通电力流，研究人员基于最优潮流与交通分配问题(traffic assignment problem，TAP)，提出最优交通电力流模型.基于静态交通流分配问题，文献[5-6]分别在无线充电、快速充电等补能模式下，提出了面向UCTPSs 的静态交通电力流模型，并在社会效益最大化[5]、用户利益均衡[6]的模式下，提出了相应的分析方法.为进一步描述交通电力流的时间特性，研究人员基于半动态TAP[7]、动态TAP[8]对静态交通电力流进行扩展，考虑时变的交通出行量，形成了动态最优交通电力流(dynamic optimal traffic power flow，DOTPF)问题.在构建的动态交通电力流模型中，文献[7]采用半动态TAP 刻画了交通流在中短期内的传播以及需求在相邻时段内的分配特性.进一步地，文献[8]采用动态TAP 考虑了多段短期内变化的出行需求分配以及交通流分布特性.

此外，电力交通流的时空分布受到UCTPSs 阻塞的影响.UCTPSs 阻塞可出现在道路[9]、输电线路[8]、充电设施[8]处.文献[10]通过引入道路容量、充电站容量约束，避免UCTPSs 内出现阻塞现象；文献[11]利用时空网络(time space network，TSN)提出了应对配电系统阻塞、电压安全约束下移动储能车的调度方法.上述研究表明，阻塞影响通行时间、充电时间及供电能力，改变交通流、电力流的时空分布，进而影响电动汽车的移动储能特性.

为实现低碳目标，一方面，本地可再生能源并网比例将提高，而电网需具备更好的调控能力以应对可再生能源自身的气候条件依赖性诱发的波动性、间歇性等；绿色出行等理念也促进了网约车等运营车辆全面电气化.另一方面，运营电动汽车在充电设施处，可向电网放电，作为储能提高城市电网的可再生能源的消纳能力.因此，在DOTPF 中应当考虑充电站模型由可控负荷向储能电站的演化.

然而，目前的模型中尚未计及多重阻塞环境下，电动汽车移动、静止、排队、充电的状态转换关系，且功率、能量状态离散，无法准确量化电动汽车并网的充放电特性.此外，现有DOTPF 以电网经济性、路网通行时间为导向，未计及发电过程的碳排放.

为分析低碳、阻塞环境下的城市电网、充电设施、道路网络在电动汽车时空移动过程中交通、电流时空分布，本文提出了带队列时空网络模型，以表示阻塞环境下电动汽车的移动、静止、排队、充电状态转换关系；然后提出了考虑经济性、碳排放、交通需求等多目标的DOTPF 模型.

1 UCTPSs

典型的UCTPSs 如图1 所示.该系统由城市电网、充电设施、城市路网构成.本文采用有向图表示电力节点、充电站、交通节点间的链接关系；i∈N，c∈C，s∈S，w∈W，m∈M分别表示电力节点、充电站、储能电站、可再生能源场站、交通节点集合.ij∈E表示线路集合；l∈L表示道路集合.对于任意的充电站c∈C，其电能由电网提供.其中，(N∪C，E)和(C∪M，R)构成的子图联通.

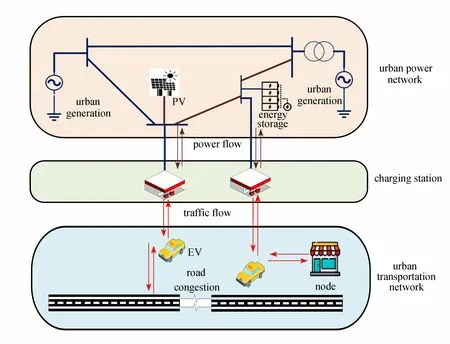
图1 UCTPSs 示意图Fig. 1 Schematic of UCTPSs

城市电网内的电力节点由城市供电电源、储能、本地可再生能源构成，经过输电线路联结.城市路网内的节点包含出发节点、终止节点、中间节点等.如图1 所示，电动汽车在城市路网内移动形成交通流，经过充电设施与城市电网进行双向电力流交互.

为便于分析，与现有研究一致[5,8]，本文以城市高压配电网为研究对象，采用直流潮流描述城市电网潮流分布；城市路网内假设仅含有纯电动汽车，其被划分为有限的车队集合v∈V；每个车队v的时空移动、充放电过程可表述为车辆的调度问题.系统调度时间被划分为T个等时间步长Δt区间.

2 基于队列时空网络的动态交通分配模型

为描述离散时间环境中交通网阻塞状态下，电动汽车在充电站及交通节点的时空移动特性，本节构建队列时空网络模型，以表示电动汽车在充电设施进行排队时的储能特性.

2.1 含队列的时空网络模型

对路网进行时间的拓展，如图2 所示，图2 (a) 表示原始路网，权重为距离.图2 (b)中距离转化为通行时间，并引入表示充电站内队列的排队节点.对任意车队v，其对应的时空网络可表述为以下加权有向图＜Mv∪Cv∪Qv∪{Ov,Dv}，Av，Wv＞.其中，Mv，Cv，Qv表示车队v在给定时间集合T内交通节点、充电站、队列的空间位置集合，即Cv: =∏t∈TCt，Mv: =∏t∈TMt，Qv: =∏t∈TQt，ct=Ct(c)，mt=Mt(m)，qt=Qt(q)，∀t∈T；Ov和Dv为车队v的初始节点和最终节点；ζij∈Av表示不同节点间空间或时间的转移关系，包含移动弧AM,v、静止弧AS,v、初始弧AO,v、终点弧AD,v、预排队弧APQ,v、排队弧AQ,v、预充电弧APC,v、充放电弧AC,v、满充弧AF,v.决策变量ζij=1 表示该弧属于最优路径，否则ζij=0.

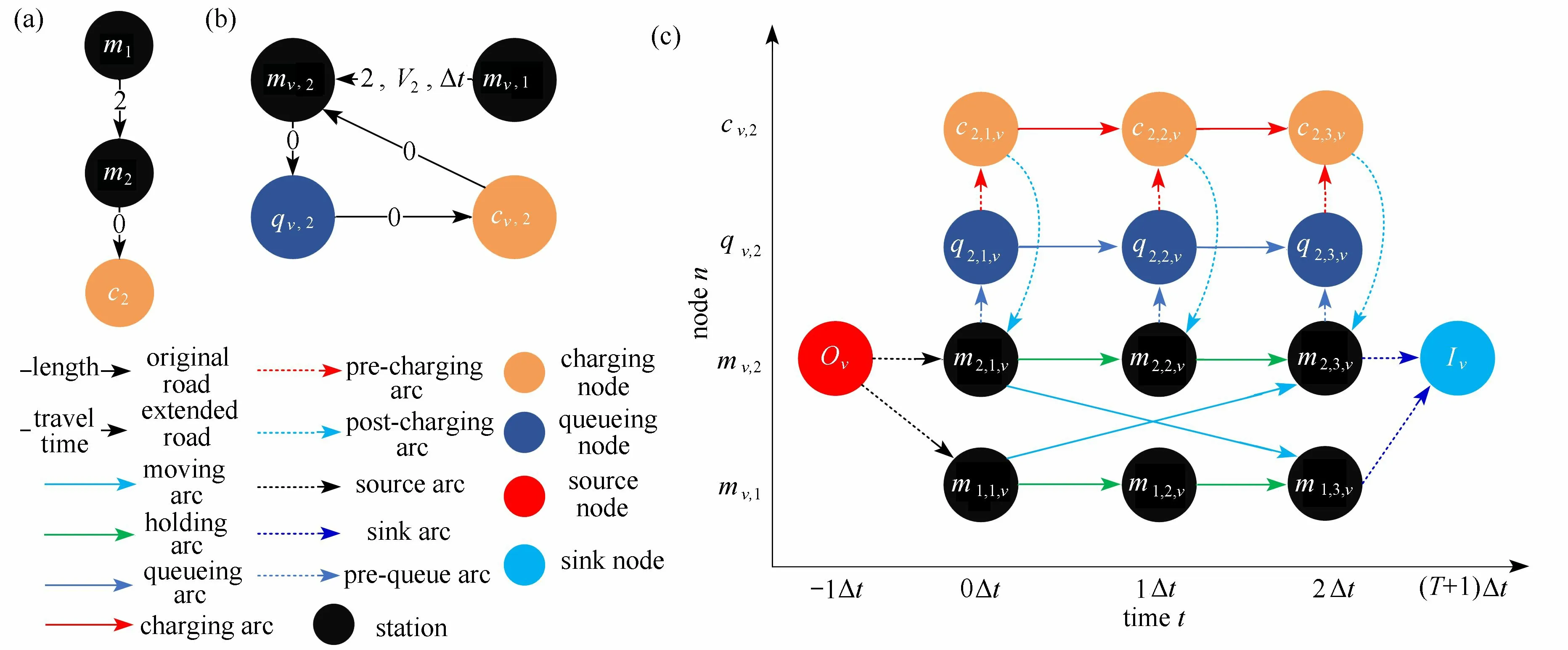
图2 队列时空网络Fig. 2 Time-space networks with queues

需要说明的是，与常规时空网络不同[8,11]，本文在每个充电站内引入了一个排队节点Qc，以表示充电设施有限时，车队从接入充电站到开始充电前的排队状态.

对于图2 中构建的时空网络，基于流量守恒等条件，构建以下约束集合，表示车队v在不同节点及不同状态间的转换关系：

式(1)表示初始位置约束，式(2)表示最终位置约束，式(3)表示空间节点约束，式(4)表示排队节点约束，式(5)表示充电站节点约束.

2.2 基于队列时空网络的车辆调度模型

基于图2、式(1) ～ (5)构建的队列时空网络模型，任一车队v的车辆调度模型可表述为以下混合整数线性规划模型：

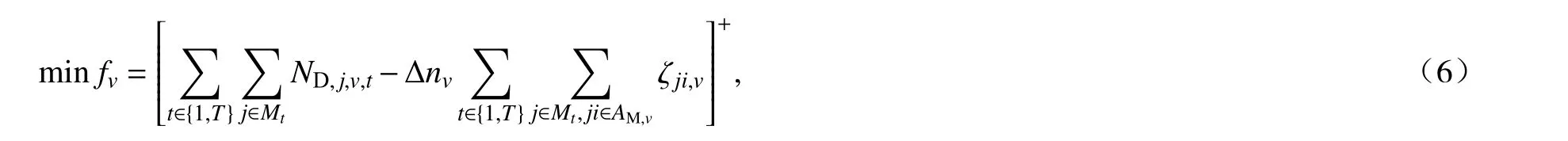
式中，fv是车队v的交通出行损失量，即未满足的交通需求量；ND,j,v,t是车队v时段t收到节点j的出行服务指派量，由2.3 小节中动态交通流指派生成；Δnv为车队v的载客量.式(6)中，函数[x]+定义为max{x,0}，即当电动汽车可提供的载客量超过需求量时，未完成的交通出行量，交通损失为0；反之，则载客量小于需求量，则记入交通损失.

在车辆调度过程中还需满足各时刻的能量约束.车队v在各节点j处的能量状态，可表示如下：

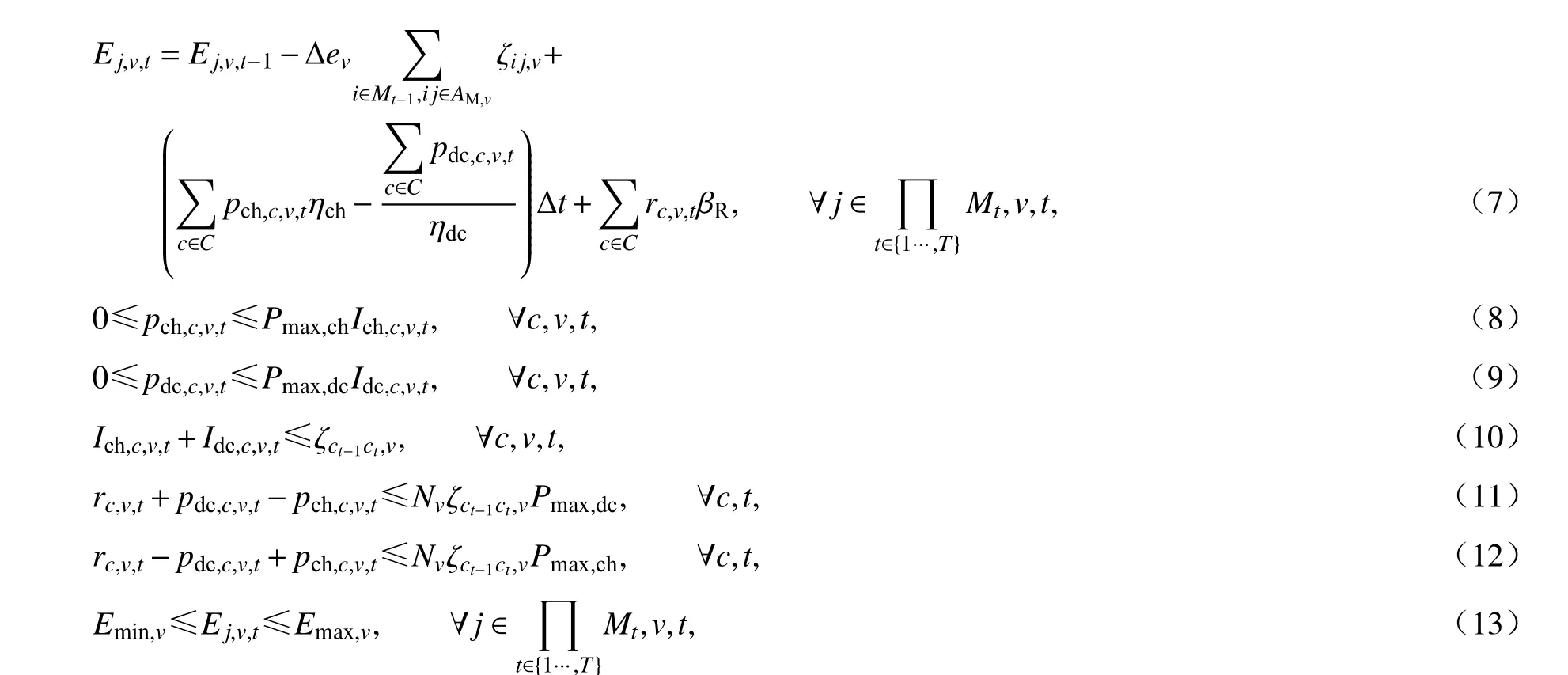
式中，Ej,v,t是表示节点j车队v时刻t的能量状态；Δev表示车队v的单位能耗；pch,c,v,t，pdc,c,v,t和rc,v,t分别表示充电设施c处车队v时段t的充电、放电功率及正负对称的备用容量[12]；βR为备用调用对充电过程的影响；Ich,c,v,t和Idc,c,v,t是二进制变量，为车队v充电或放电的状态标识；Pmax,ch和Pmax,dc表示充电桩的充电、放电额定功率；Emax,v和Emin,v表示车队v的最大和最小能量约束；ηch和ηdc表示充放电效率，Nv表示车队v的车数.

式(7)表示车队v的动态能量变化，式(8)、(9)表示充放电功率约束，式(10)表示充放电状态约束，式(11)、(12)表示计及备用约束后的容量约束，式(13)为车队v的能量状态约束.

为表示充放电、移动、静止、排队状态之间的互斥性，引入以下约束条件：

同时，车辆调度模型中，还需要满足式(1) ～ (5)所示的队列时空网络约束条件.

2.3 动态交通流分配模型

为满足不同空间节点处的时变出行需求，基于各车队的交通服务能力，构建以下动态交通流分配模型：

由于道路r的容量、充电设施c的容量及排队q的容量有限，引入式(17) ～ (20)控制阻塞程度，即道路、充电设施以及队列长度流量不超过相应的容量，道路上车队的通过时间为自由通行时间与排队时间之和，充电设施内车队的停留时间为充放电时间与排队时间之和.

式中，fl,t为道路l时段t上的流量，即所对应的弧ij上的流量.以图2(c)为例，道路(m1,m2)在时刻1 对应弧ζ(m1,1,m2,3)，道路(m1,m2)在时刻2 对应弧ζ(m1,2,m2,4).

聚合各车队的充放电功率及备用容量，充电站c处的充放电功率及备用容量可表示为

式中，Pch,c,v,t，Pdc,c,v,t和rc,v,t分别表示充电站c时段t的充电、放电功率及备用容量[12].

3 动态低碳经济调度建模

汇聚本地可再生能源、城市电网供电电源、城市电源，本节构建多目标动态经济调度模型，通过优化常规机组、储能及电动汽车充电站的调度计划，在满足城市电网安全运行的前提下，同时减少发电成本、碳排放.

动态低碳经济调度满足常规机组、储能、线路安全、功率平衡、备用容量约束，如下：

1）常规机组约束

式中，g∈G为发电机组集合；Pmin,g和Pmin,g分别为最小和最大技术出力；Rg,60,+，Rg,60,-和Rg,10,+分别为60 min和10 min 的爬坡速率.

式(23)、(24)为考虑备用后的发电机容量约束，式(25)为发电机提供备用容量约束，式(26)、(27)为机组爬坡速率约束[13].

2）储能约束

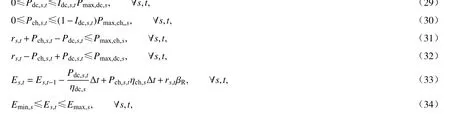
式中，Pmax,ch,s和Pmax,dc,s表示储能电站s的充电、放电额定功率；Emax,s和Emin,s表示储能电站s的最大和最小能量约束；Pch,s,v,t，Pdc,s,v,t和rs,t分别表示储能电站s时段t的充电、放电功率及备用容量.

式(29)、(30)表示储能电站s的充放电功率约束，式(31)、(32)表示计及备用约束后储能电站s的容量约束，式(33)、(34)表示储能电站s的动态能量变化、能量状态约束.

3）线路安全约束

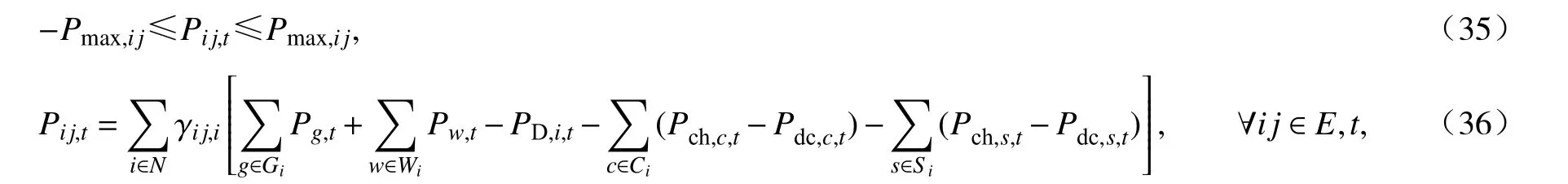
式中，Pij为输电线路ij上的传输功率；γij,i为节点i对于支路ij的潮流转移因子[14]；Pmax,ij为输电线路ij上的最大传输功率限制.

4）功率平衡约束

式中，a2,g，a1,g，a0,g为常规机组的发电成本系数，b2,g，b1,g，b0,g为常规机组的碳排放系数.需要说明的是，本文的研究对象为电动汽车，不考虑燃油汽车；交通网内的碳排放均来自电动汽车.同时，式(21)、(22)、(37)表明电动汽车的电能来自城市电网，而城市电网的碳排放来自式(40)内常规机组的发电过程.因此，本文中UCTPSs 的碳排放仅来自发电机组的碳排放.

4 多目标动态交通电力流模型

基于构建的动态交通分配模型、动态低碳经济调度模型，本节构建如下的多目标优化模型：

由于集合X为线性集合，x为混合整数向量，式(41)为混合整数二次规划多目标优化模型.同时，由于a2,g和b2,g非负，该问题为凸.可采用字典序法[15]、线性加权[16]等方法将其转换为单目标优化问题.

基于目前的碳排放价格λcarbon及交通出行订单损失惩罚价格λunmet，可以通过式(38)中的发电成本、碳排放及交通出行损失转转为总成本函数：

式(42)为混合整数凸二次规划问题，可采用Gurobi、Cplex 等商业求解器求解.

5 算 例 分 析

5.1 算例描述

为测试所提出模型的有效性，基于IEEE-30 节点及Sioux Falls 路网系统[17]构建两个大小规模不同的测试算例.发电机组成本参数如文献[18]所示；时间步长Δt=1 h；λcarbon=8.12 $/吨，λunmet=5 $/辆.各算例采用Gurobi 9.5 求解，计算环境为Intel Xeon Gold 6226R*2，128 GB RAM.

测试系统1 由 IEEE-30 系统内的节点1 ～ 4 及Sioux Falls 路网中的节点21 ～ 24 所组成.电力节点1 和2 分别接入机组1 与机组2.电力节点3 接入位于交通节点4 的充电站2.电力节点4 接入电池储能电站1 座，容量为20 MW/20 MWh，ηch=0.95，ηdc=0.9，初始能量状态为10 MWh，Emax,s= 18 MWh，Emin,s= 2 MWh；同时，接入50 MW 光伏电站1 座，位于交通节点2 的充电站1.路网系统内含有2 组交通需求，在8:00—15:00 由交通节点1 到节点3，以及在14:00—21:00 由交通节点3 到节点1，需求量为5 700 和5 600；交通需求分配至4 个车队，每个车队的规模是800 辆，通行速度为每小时1 单位距离，每辆车的充放电功率为33 kW.为说明道路、充电设施、线路阻塞及其组合对发电成本、碳排放及出行损失的影响，构建表1 所示的对比情景.

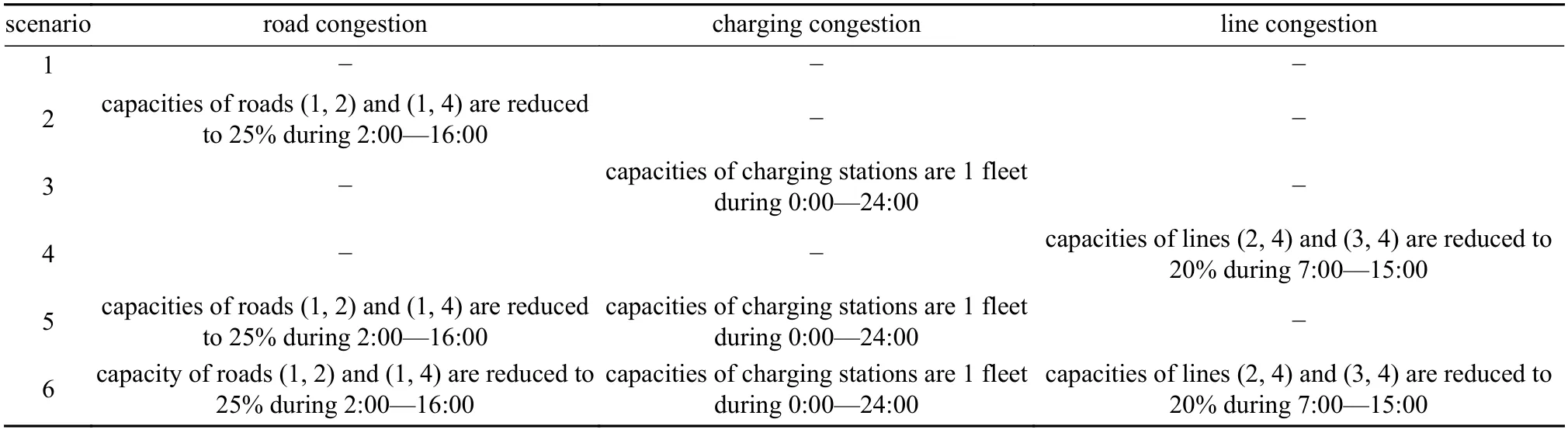
表1 仿真情景设计Table 1 Simulation scenarios

如图A1 所示，测试系统2 由 IEEE-30 系统以及Sioux Falls 路网构建.电力节点7 接入光伏电站1 座，装机容量为50 MW，并接入位于交通节点11 的充电站1.充电站2 连接电力节点25 与交通节点16，充电站3 连接电力节点11 与交通节点21.电力节点4 和24 各接入1 座20 MW/20 MWh 的储能电站.路网系统内选取4-10、7-10、13-10、20-10 等包含来回的4 组交通需求，在8：00 时从交通节点10 出发，在13:00 开始返回交通节点10，需在5 h 内完成，由21 条车队满足，每条车队规模为600 辆.道路阻塞设置为所有道路通行容量减少至30%，充电设施阻塞设置为1 时段内仅2 车队，线路阻塞设置为所有线路容量减少至80%.

图A1 测试系统2 单线图Fig. A1 Single line diagram for case 2

5.2 算例分析

5.2.1 阻塞对系统运行影响

测试系统1 中，不同情景下的总成本、发电成本、碳排放量、交通出行损失见表2.可见，随着系统内阻塞情况的恶化，总成本逐渐增加，最终增加了15.01%.系统内主要成本的增加由交通出行损失引起，交通出行损失增加了65.30%.

表2 测试系统1 各情景下计算结果Table 2 Results under different scenarios for case 1

不同情景下，电动汽车充电站的充放电曲线如图3 所示；其中正值为放电，负值为充电.由情景1 和情景2 中总负荷曲线对比可知，道路阻塞导致10：00—12：00 的充电负荷降低；情景3 中充电站阻塞与情景4 中线路阻塞会限制充电供给，使出行车辆减少；进一步地，情景2 和情景5 中负荷曲线差异的表明，充电站阻塞导致充电负荷向10：00—11：00 转移；情景6 中，在道路、充电站、线路同时阻塞时，充电负荷由10：00—12：00转移至14：00—18：00，同时电动汽车可向电网内注入更多功率.可见，阻塞会显著影响充电负荷的时序过程；仅发生一种阻塞时，线路阻塞对充电功率的影响最大；道路、充电站、线路同时阻塞时，充电负荷发生时移最大.

在测试系统1 内，共有4 个车队.情景1 及情景6 下各车队位置(包含节点和队列)的时间变化如图A2 及图A3 所示.为满足用户从节点1 到节点4 的出行需求，在情景1 下，车队1、2、3、4 分别在8：00、9：00 由节点1 驶向交通节点4，并在充电站2 进行充电，形成图3 中11：00—12：00 的充电高峰.在道路、充电站、线路阻塞时，如图A3 所示，各车队的行驶特性发生显著变化.为减少线路阻塞的影响，车队2 由交通节点1 行驶至交通节点2，并在充电站1 提前充电.

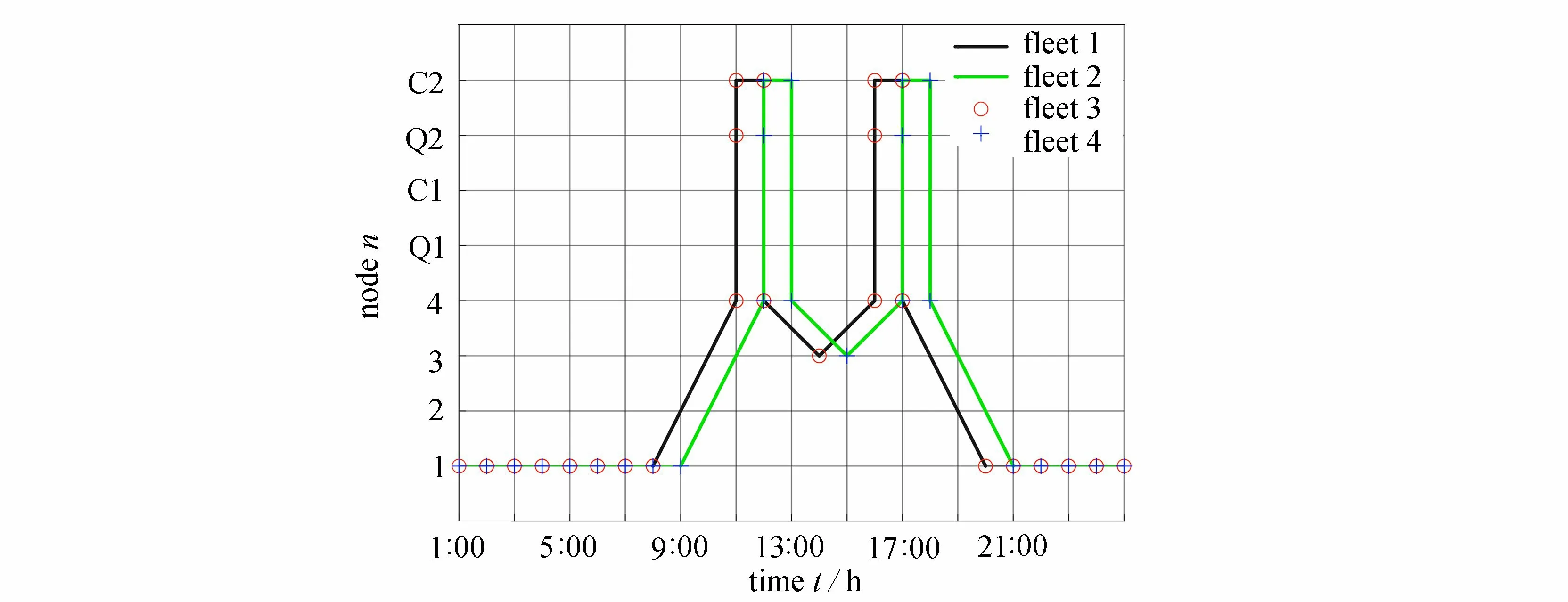
图A2 情景1 下的车队移动曲线Fig. A2 Routine of electric vehicles fleets under scenario 1

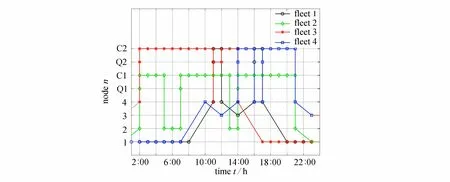
图A3 情景6 下的车队移动曲线Fig. A3 Routine of electric vehicles fleets under scenario 6

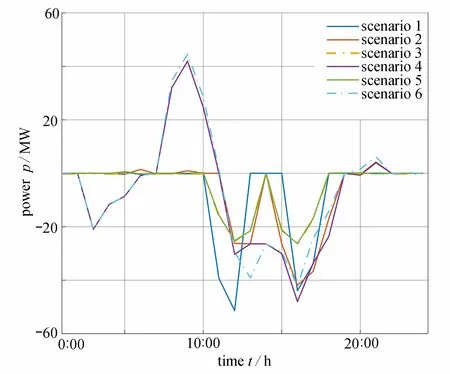
图3 不同情景下总充放电负荷曲线Fig. 3 Total charging/discharging load profile under different scenarios

为说明线路阻塞对潮流以及充电行为的影响，情景1 与情景4 中线路(3，4)的传输功率如图4 所示.为满足线路传输功率约束，线路(3，4)的阻塞使得传输功率由13:00—15:00 转移至8:00—12:00.

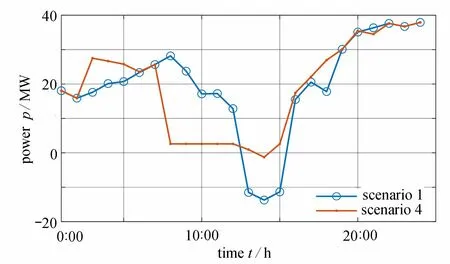
图4 情景1 和情景4 下线路(3, 4)传输功率Fig. 4 Power flow on line (3, 4) under scenarios 1 and 4

为说明道路阻塞对交通流以及充电负荷的影响，情景1 与情景2 下的道路流量分布如图5 所示.受到道路通行容量的限制，道路(1，4)的阻塞使得通行流量在8:00—11:00 降低且产生滞后，改变位于交通节点4 的充电站1 的车辆到达过程，进而影响图3 中充电功率的时间分布.

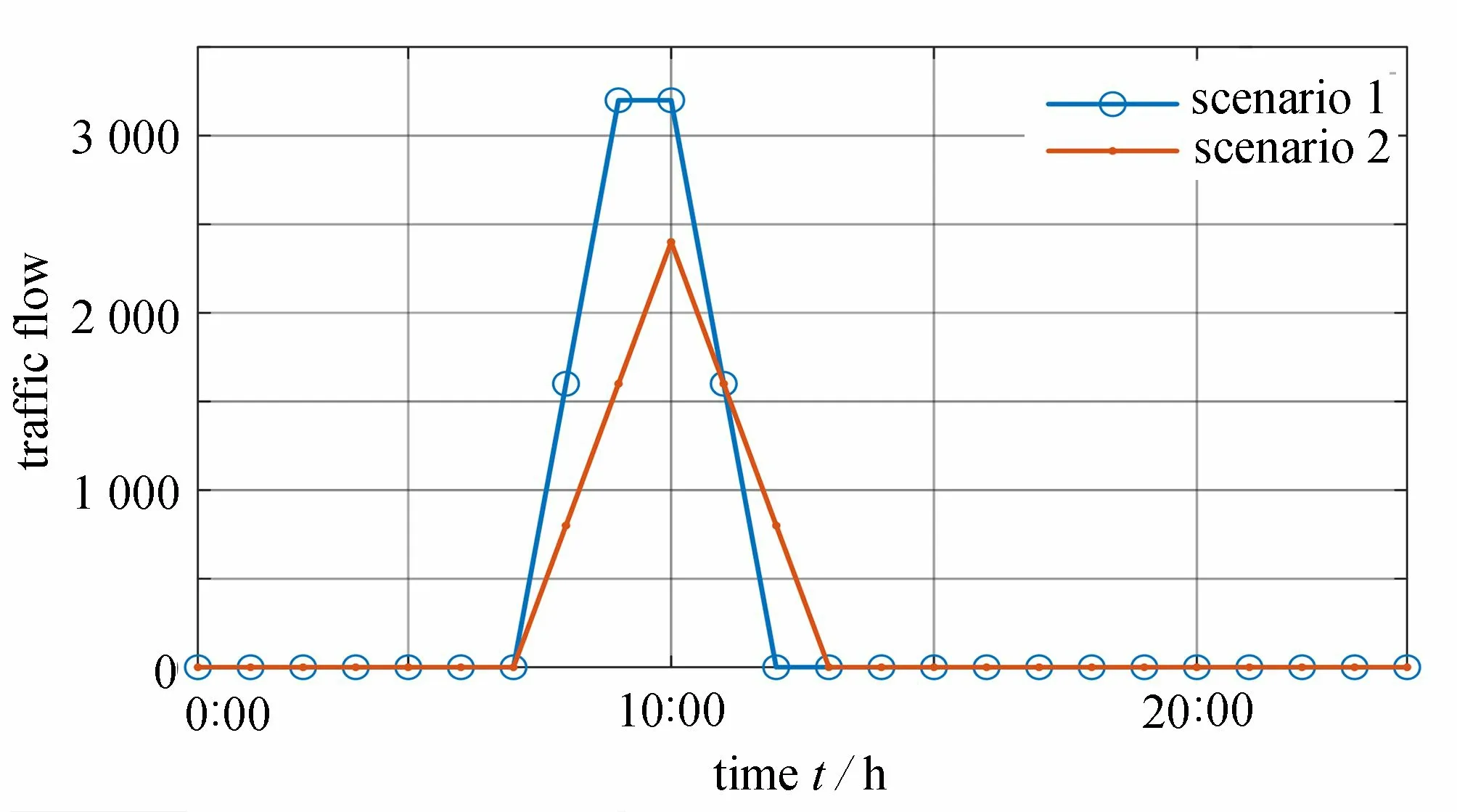
图5 情景1 和情景2 下道路(1, 4)流量Fig. 5 Traffic flow on road (1, 4) under scenarios 1 and 2

5.2.2 网络规模对系统运行影响分析

为说明不同电网规模下，阻塞对城市电网和交通网络的影响，测试系统2 中不同场景下的总成本、发电成本、碳排放量、交通出行损失见表3.可见，随着系统内阻塞情况的恶化，总成本逐渐增加，增加了10.06%.与测试系统1 对比说明，网络规模的增大而产生的冗余性可弱化阻塞影响.

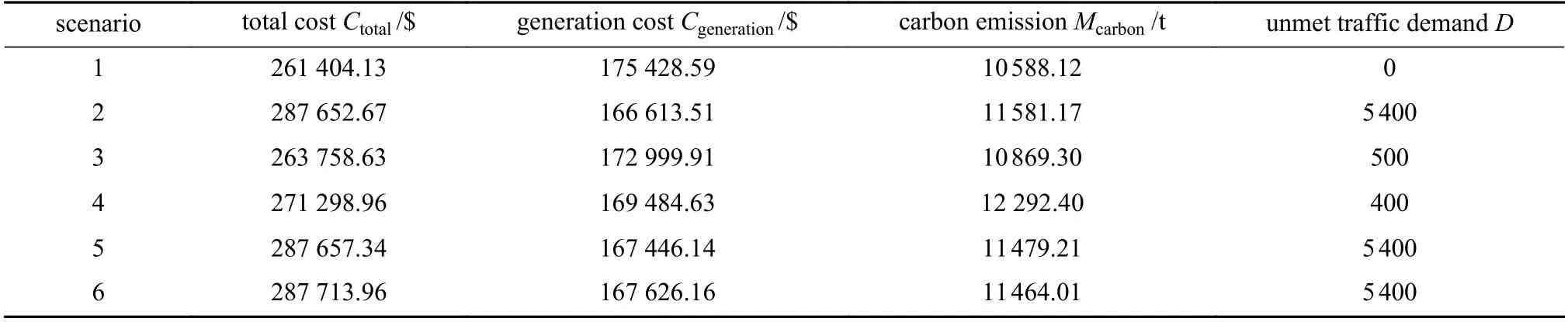
表3 测试系统2 各情景下计算结果Table 3 Results under different scenarios for case 2

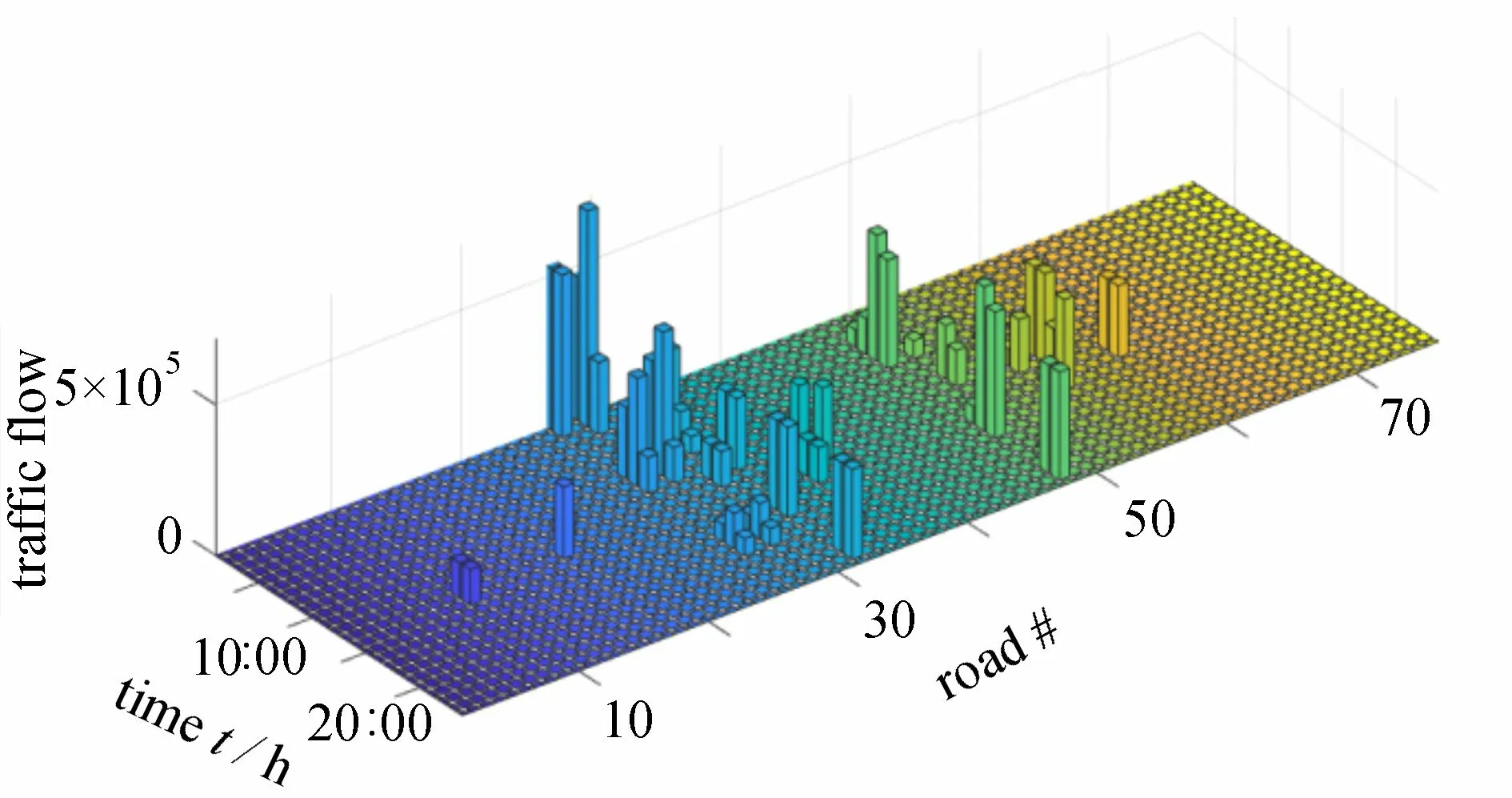
情景1 及情景6 下，线路潮流及道路车流分布见图A4 ～ A7.可见，阻塞显著改变了城市道路内的车流分布，使得系统内的发电成本降低，但系统的碳排放增加了8.27%.进一步地，为验证车队规模对所提出模型求解效率的影响，情景1 下不同车队规模的计算时间与上下界差距见表4.其中，上下界差距为Gurobi 所采用空间分支定界中上界与下界的差距.可见，随着车队规模的增加，求解时间及上下界呈现非线性增加的趋势.在实际应用本文所提出的模型时，仍需对大规模电动汽车进行聚合，以平衡计算时间及计算复杂度.

图A4 测试系统2 情景1 下潮流分布图Fig. A4 Power flow of case 2 under scenario 1

表4 测试系统2 情景1 不同车队下的计算时间与差距Table 4 CPU time and gap under different size of fleets in scenario 1 for case 2

6 结 语

本文以城市交通-电力耦合系统为研究对象，以电动汽车的动态交通分配为切入点，以改善系统碳排放、经济性和交通出行损失为目标，构建了最优动态交通电力流模型，对各电动汽车车队、常规机组和储能进行调度，形成了多目标混合整数二次规划问题.进而基于碳排放价格、出行损失价格，将多目标问题转换为单目标问题进行求解.以IEEE-30 节点、Sioux Falls 路网耦合系统为测试算例，通过对比分析，验证了本文提出的动态交通电力流模型应对道路、充电设施、线路及其组合阻塞的适用性.

本文是对城市内电力及交通融合建模的一次尝试.对交通分配模型可进一步完善，例如考虑用户满意度以及放电补贴等用户特性；面对在UCTPSs 自身的多主体，以及在模型中变量过多而难以求解的问题，在未来的工作中考虑多主体分层、分布式建模[19]与求解方法；同时，在处理可再生能源、负荷等不确定方面，需采用随机、鲁棒、分布鲁棒等方法处理相应的不确定因素.

附 录

图A5 测试系统2 情景1 下车流分布图Fig. A5 Traffic flow of case 2 under scenario 1

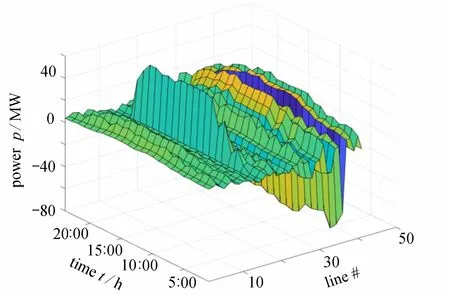
图A6 测试系统2 情景6 下潮流分布图Fig. A6 Power flow of case 2 under scenario 6

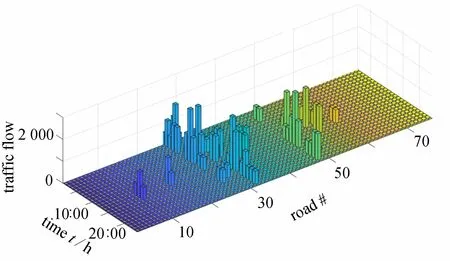
图A7 测试系统2 情景6 下车流分布图Fig. A7 Traffic flow of case 2 under scenario 6

参考文献（ References ） ：

［1］ 杨天宇, 郭庆来, 盛裕杰, 等. 系统互联视角下的城域电力-交通融合网络协同[J]. 电力系统自动化, 2020, 44（11）: 1-9. （YANG Tianyu, GUO Qinglai, SHENG Yujie, et al. Coordination of urban integrated electric power and traffic network from perspective of system interconnection[J].Automation of Electric Power Systems, 2020,44（11）: 1-9.（in Chinese））

［2］ 李秋硕, 肖湘宁, 郭静, 等. 电动汽车有序充电方法研究[J]. 电网技术, 2012, 36（12）: 32-38. （LI Qiushuo, XIAO Xiangning, GUO Jing, et al. Research on scheme for ordered charging of electric vehicles[J].Power System Technology, 2012, 36（12）: 32-38.（in Chinese））

［3］TONG Li, ZHAO Shen, JIANG Hang, et al. Multi-scenario and multi-objective collaborative optimization of distribution network considering electric vehicles and mobile energy storage systems[J].IEEE Access, 2021, 9:55690-55697.

［4］ 苏粟, 李玉璟, 夏明超, 等. 基于时空耦合特性的充电站运行状态预测[J]. 电力系统自动化, 2022, 46（3）: 23-32. （SU Su, LI Yujing, XIA Mingchao, et al. Operation state prediction of charging station based on spatio-temporal coupling characteristics[J].Automation of Electric Power Systems, 2022, 46（3）: 23-32.（in Chinese））

［5］WEI Wei, MEI Shengwei, WU Lei, et al. Optimal traffic-power flow in urban electrified transportation networks[J].IEEE Transactions on Smart Grid, 2017, 8（1）: 84-95.

［6］ 谢仕炜, 林伟伟, 张亚超. 基于变分不等式理论的电力-交通耦合网络均衡状态研究[J]. 中国电机工程学报, 2022,42（17）: 6220-6239. （XIE Shiwei, LIN Weiwei, ZHANG Yachao. Research on coupled power-transportation network equilibrium state based on variational inequality theory[J].Proceedings of the CSEE, 2022, 42（17）: 6220-6239.（in Chinese））

［7］LV Si, WEI Zhinong, SUN Guoqiang, et al. Optimal power and semi-dynamic traffic flow in urban electrified transportation networks[J].IEEE Transactions on Smart Grid, 2019, 11（3）: 1854-1865.

［8］ZHOU Zhe, ZHANG Xuan, GUO Qinglai, et al. Analyzing power and dynamic traffic flows in coupled power and transportation networks[J].Renewable and Sustainable Energy Reviews, 2021, 135: 110083.

［9］ 张鹏, 吕瑜佩, 郭明旻, 等. 简单闭环路网交通流定常解[J]. 应用数学和力学, 2021, 42（2）: 123-132. （ZHANG Peng,LÜ Yupei, GUO Mingmin, et al. Steady-state solutions of traffic flow in a simple circled road network[J].Applied Mathematics and Mechanics, 2021, 42（2）: 123-132.（in Chinese））

［10］ESTANDIA A, SCHIFFER M, ROSSI F, et al. On the interaction between autonomous mobility on demand systems and power distribution networks: an optimal power flow approach[J].IEEE Transactions on Control of Network Systems, 2021, 8（3）: 1163-1176.

［11］LIU Xiaochuan, SOH C B, ZHAO Tianyang, et al. Stochastic scheduling of mobile energy storage in coupled distribution and transportation networks for conversion capacity enhancement[J].IEEE Transactions on Smart Grid, 2021, 12（1）: 117-130.

［12］LI Nan, UÇKUN C, CONSTANTINESCU E M, et al. Flexible operation of batteries in power system scheduling with renewable energy[J].IEEE Transactions on Sustainable Energy, 2015, 7（2）: 685-696.

［13］ 赵天阳, 张华君, 徐岩, 等. 不确定环境下含云计算数据中心的电网韧性增强调度[J]. 电力系统自动化, 2021, 45（3）:49-57. （ZHAO Tianyang, ZHANG Huajun, XU Yan, et al. Resilience-enhanced scheduling of power system with cloud computing data centers under uncertainty[J].Automation of Electric Power Systems, 2021, 45（3）: 49-57.（in Chinese））

［14］RAHMANI M, KARGARIAN A, HUG G. Comprehensive power transfer distribution factor model for large-scale transmission expansion planning[J].IET Generation,Transmission & Distribution, 2016, 10（12）: 2981-2989.

［15］ZHONG Shaopeng, JIANG Yu, NIELSEN O A. Lexicographic multi-objective road pricing optimization considering land use and transportation effects[J].European Journal of Operational Research, 2022, 298（2）: 496-509.

［16］MARLER R T, ARORA J S. The weighted sum method for multi-objective optimization: new insights[J].Structural and Multidisciplinary Optimization, 2010, 41（6）: 853-862.

［17］CHAKIROV A, FOURIE P J. Enriched Sioux Falls scenario with dynamic and disaggregate demand[J].Arbeitsberichte Verkehrs-und Raumplanung, 2014: 978.

［18］ 张展鹏, 班明飞, 郭丹阳, 等. 适用于环境-经济调度研究的燃煤机组二氧化碳排放特性模型[J]. 上海交通大学学报,2021, 55（12）: 1663-1672. （ZHANG Zhanpeng, BAN Mingfei, GUO Danyang, et al. A model for carbon diosixde emission characteristics of coal-fired unit for environment-economic dispatch research[J].Journal of Shanghai Jiaotong University, 2021, 55（12）: 1663-1672.（in Chinese））

［19］ 肖勇, 喻洁, 张新森, 等. 泛在电力物联网下用户侧分布式电源P2P优化调度研究[J]. 应用数学和力学, 2020, 41（12）:1358-1368. （XIAO Yong, YU Jie, ZHANG Xinsen, et al. Research on P2P optimal scheduling of user side distributed generation under ubiquitous power internet of things[J].Applied Mathematics and Mechanics, 2020, 41（12）:1358-1368.（in Chinese））