OFDM 雷达通信一体化的同频干扰抑制技术

胡邓雨 谢 锐 罗 锴 陈 达

（1.华中科技大学网络空间安全学院，湖北武汉 430074；2.华为技术有限公司西安研究所，陕西西安 710077；3.中国兵器装备集团上海电控研究所，上海 200092）

1 引言

随着信息技术的发展，作战平台需要装备越来越多的电子设备［1］，占用大量空间、设计复杂、相互之间可能会产生电磁干扰［2］。雷达通信一体化系统（Integrated Radar and Communication System，IRCS）可以提高设备的可用性和可靠性，降低设备间电磁干扰，是解决上述问题的有效途径之一。另外，IRCS 还可以应用于第六代（Sixth Generation，6G）移动通信网络［3-6］。基于6G 移动通信网络的IRCS 可以在保持低延时、超可靠通信的同时，实现雷达组网探测，这有助于基站探测用户数量和位置，从而更好地分配资源和服务用户，提高了频谱利用率和用户体验。综上所述，无论在军事上还是民用上，IRCS已成为必然发展趋势。

IRCS 的实现方式多样，基于现有的硬软件技术水平，其设计可以从时域、频域、空域等多个角度考虑［7-9］。但是，这些方案必须牺牲一部分雷达或者通信性能，以使雷达和通信功能在同一个域中实现。因此，其资源利用率并不高。为了提高时频资源的利用率，提升IRCS 的集成程度，基于共享波形的IRCS 得到关注［10］，该方案发射一种信号，可以同时实现通信和探测两种功能。有助于提高资源利用率，缩减设备体积，减少能量消耗。正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）是一种良好的共享波形，具有较好的信息传输能力、较高的频谱利用率等优点，在无线通信中被广泛使用［11-12］。同时，OFDM 信号具有良好的模糊函数低旁瓣特性，拥有良好的雷达应用前景［13-15］。因此，基于OFDM 的IRCS具有较好的研究价值和实现意义。在基于OFDM 的IRCS 中，IRCS 节点同时同频发送共享波形，产生同频干扰。就通信而言，其他节点的信号导致通信信干比（Signal to Interfer⁃ence Ratio，SIR）降低，误码率升高，影响通信质量。就雷达而言，其他节点直达波为单程信号，目标回波为双程信号，直达波功率远大于目标回波［16-17］，导致噪声基底抬高，检测概率降低，探测距离减小，严重时完全湮没目标。当前针对IRCS 同频干扰的研究较少，相关研究尚处于起步阶段。因此，综合考虑雷达和通信性能，有效抑制OFDM IRCS同频干扰是一个值得研究的问题。

在无线通信领域中，不考虑空域时，常用干扰协调［18-19］、干扰随机化［20］和干扰消除［21］等方法抑制同频干扰。干扰协调技术通过对频谱等资源进行规划来进行干扰抑制，频率复用［18-19］可以有效抑制同频干扰，提高边缘用户的体验，但其频率利用率较低。干扰随机化技术［20］通过将干扰信号随机化为“白噪声”，从而抑制小区间干扰，但此算法无法改变干扰能量，不适用于干扰较强的场景。干扰消除技术［21］通过对干扰信号进行解调和解码，然后将干扰信号进行重构后，再用接收信号减去重构信号，以实现干扰消除，当干扰重构较为准确时，可以有效抑制同频干扰。基于此干扰重构算法，文献［16-17，22］使用串行干扰消除技术［21］来抑制IRCS同频干扰，当存在多个功率相近的干扰信号时，干扰信号很难准确解调和重构，导致干扰无法准确滤除，仍会影响目标参数估计。文献［23］提出了交织OFDM（Interleaved OFDM，I-OFDM）IRCS，此系统中，不同一体化节点的参考子载波相同，数据子载波相互正交，可以更准确的分离接收信号，但该方法降低了频带利用率。

针对上述问题，本文首先从回波信号信干比分析了IRCS 进行同频干扰抑制的必要性。然后将交织区分多址与基于OFDM 的IRCS结合到一起，提出了一种抑制OFDM IRCS同频干扰的方法，仿真结果表明，此算法在保证频谱利用率的条件下，可以有效抑制雷达通信一体化系统的同频干扰。

2 同频干扰特性分析

2.1 信号模型

本文主要考虑单基地模型，如图1 所示的IRCS场景中，三个一体化节点发射雷达通信一体化信号来同时实现无线通信和雷达感知。将节点一作为研究节点（又称作“雷达节点”），节点二和节点三作为干扰节点（又称作“通信节点”）。

图1 同频干扰系统模型Fig.1 Co-channel interference system model

对节点一而言，接收信号包括：节点一自己发射信号（简称为“雷达信号”）的回波和静杂波、节点二和节点三发射信号（简称为“通信信号”）的直达波以及静杂波。基于图1，考虑NT个目标和NC个通信节点存在的场景。首先，记雷达节点发射信号为x(t)，第i个目标到雷达节点的距离为Ri，相对速度为vi，路径损耗为γi，则IRCS 的雷达回波信号可以表示为

其中c 表示光速，λ表示信号波长。此外，考虑目标节点自身发射信号的静杂波yrc(t)，记自身发射信号的静杂波数为Nrc，第j个静杂波的路径长度为Rj，路径损耗为γj，则有

其次，我们还应考虑NC个通信节点对雷达节点产生的直达波和静杂波的干扰。对第k个通信节点而言，其发射信号为xk(t)，其到达雷达的信道响应是hk(t)，则雷达节点接收到的通信信号可以表示为

假设第k个通信节点到达雷达节点的直达波和静杂波总数为Nk，记其通过第l个直达波（或静杂波）到雷达节点的距离为Rk，l，路径损耗为γk，l，则信道响应hk(t)可以表示为

这样，雷达节点接收到的通信信号可以进一步表示为

综上，雷达节点接收到的信号包括NT个目标的回波信号和NC个通信节点的通信信号，即可以表示为

其中，w(t)表示加性高斯白噪声。式（4）表明，在雷达通信一体化系统中，雷达节点接收到的目标回波不仅受到传统雷达静杂波的干扰，还收到邻近通信节点的同频通信信号干扰。这些干扰会造成回波信号的信干比降低，从而导致模糊函数噪声基底抬高等问题。下面将从信干比角度分析雷达通信一体化同频干扰特性。

2.2 回波信号信干比分析

传统雷达的回波信号的信干比特性主要由雷达信号的静杂波对目标反射的回波信号的干扰特性决定的，而雷达通信一体化系统中，对目标反射回波的干扰不仅包括雷达静杂波，还包括邻近通信节点的通信信号。因此，本小节根据雷达通信一体化系统中雷达节点接收信号的数学模型来分析其信干比的特性。

通常情况下通信信号的直达波功率远大于反射路径即静杂波的功率，因此，为了简化分析，假设NC个通信节点的通信信号只包含直达波。这样，根据式（5），我们可以给出雷达节点回波的信干比的定义如下

其中，γk表示第k个通信节点直达波的路径损耗。

假设一体化节点均具有相同的发射功率Pt、发射天线增益Gt以及接收天线增益Gr，则根据雷达方程可以得到

其中σi和σj表示第i个目标和第j个静杂波的雷达散射截面积（Radar Cross Section，RCS）。而在考虑理想的自由空间传输模型下，通信信号直达波的路径损耗可以表示为

其中Rk表示第k个通信节点到雷达节点的距离。将式（8a）、式（8b）和式（9）代入式（7）得到雷达节点回波的信干比为

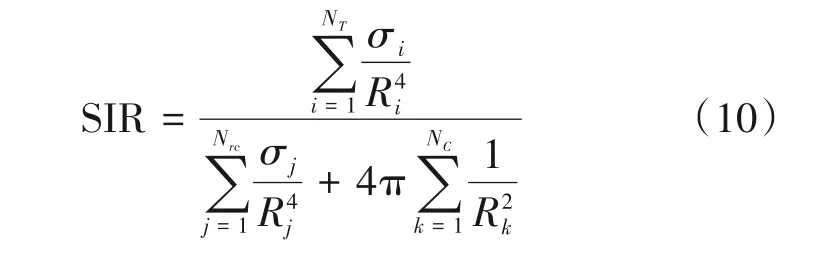
式（10）表明回波信号的信干比主要受目标RCS 和距离、雷达静杂波散射体的RCS 和距离以及通信节点到雷达节点距离这些参数的影响。相比目标RCS 和距离，当散射体的RCS 较大或距离较近时，雷达静杂波干扰加强，导致回波信干比降低，影响目标探测。更值得注意的是，目标回波对信干比的影响是目标距离的4 次方，而通信信号对信干比的影响是通信节点距离的平方，这样，即使通信节点距离较远，同频通信信号也会对雷达回波产生强干扰，导致雷达回波信干比非常低，严重影响目标探测，这是IRCS 系统特有的干扰问题，在传统雷达或通信系统中不会产生。因此，需要开展雷达通信一体化同频干扰抑制的研究。

3 同频干扰抑制算法

3.1 基于OFDM-IDMA的同频干扰抑制算法

在雷达通信一体化组网中，雷达节点的接收信号包括通信节点发送的一体化信号的直达波和静杂波、雷达节点发送信号的静杂波以及雷达目标回波。此时直达波和静杂波会产生干扰，影响目标参数估计。因此，基于OFDM 的交织区分多址（Inter⁃leave Division Multiple Access，IDMA）算法［24-25］和干扰重构消除思想，提出了基于OFDM-IDMA 的IRCS同频干扰抑制算法。具体的算法流程图如图2所示。

图2 基于OFDM-IDMA的IRCS同频干扰抑制算法流程图Fig.2 Flow chart of IRCS co-channel interference suppression algorithm based on OFDM-IDMA

图2 中，一体化节点利用OFDM-IDMA 信号进行通信和雷达探测。需要注意的是，每个一体化节点使用不同的交织序列对信号交织，才能区分出不同一体化节点发送的信号。同时，本文假设信道系数已知［24，26］。此时，雷达节点会受到通信节点发送的OFDM-IDMA 信号和静杂波的干扰。因此采用图2 中的IRCS 同频干扰抑制算法进行干扰抑制。此算法的具体流程包括雷达静杂波抑制、干扰信号分离、通信干扰重构、通信干扰抑制和目标参数估计五个过程。

1）雷达静杂波抑制。雷达静杂波影响干扰信号分离和目标参数检测，因此首先进行雷达静杂波抑制。对雷达通信一体化节点而言，雷达参考信号已知。利用已知的雷达参考信号和信道状态进行雷达静杂波重构，再利用基于干扰重构的干扰消除算法进行雷达静杂波抑制。

2）干扰信号分离。对雷达静杂波抑制后的信号进行干扰信号分离。将干扰信号作为目标信号，将雷达节点发送信号的目标回波看作干扰，然后利用不同一体化节点发送的OFDM-IDMA 信号交织方式不同来分离不同节点发送的信号，具体的信号分离流程如3.2小节所示。

3）通信干扰重构。根据上一步分离得到的通信比特流和已知信道信息，对通信节点发送的OFDM-IDMA 信号进行重构，从而恢复出雷达节点收到的通信干扰信号。

4）通信干扰抑制。由于在IRCS 信号模型中，干扰功率远大于信号功率，因此利用基于干扰重构的干扰消除技术来抑制通信信号干扰，即用接收信号减去重构的干扰信号，从而消除通信信号对目标回波的干扰，实现通信干扰抑制。

5）目标参数估计。前四步实现了IRCS 同频干扰抑制，然后需要实现目标参数估计。常用的方法为二维匹配滤波，即将干扰抑制后的信号与雷达参考信号二维互相关，从而检测出目标相对于一体化节点的距离和速度。

3.2 OFDM-IDMA原理

在无线通信系统中，为提高频谱效率和抗干扰能力，基于OFDM 的交织区分多址（Interleave Divi⁃sion Multiple Access，IDMA）算法被提出，其系统框图如图3所示。

OFDM-IDMA 系统将IDMA 系统和OFDM 系统相结合，接收端仍采用迭代多用户检测算法。需要注意的是，接收端首先要去除通信信号循环前缀并进行FFT，得到频域信号，然后再进行多用户迭代，输出各用户比特流。

首先，根据式（3），雷达节点接收到的其他通信节点的OFDM-IDMA 信号yC(t)经过FFT 后可以表示为

其中r(·)表示频域接收信号，xk(m)，m=1，2，…，M表示第k个节点发射的频域信号，NC是通信节点数量。W(·)表示均值为0，方差σ2=N0/2 的复数加性高斯白噪声的频率响应。Hk(m)为第k个用户第m个子信道的信道频率响应。ξk(m)表示来自其他K-1 个用户的干扰和噪声。将公式（11）两边同时乘以Hk(m)的共轭(m)，得到：

信号流向如图3 所示，当采用QPSK 调制时，由于Re(xk(m))和Im(xk(m))分别对应一个比特的信息，因此将接收端的实部和虚部分开处理。QPSK调制时，OFDM-IDMA 的ESE 输出信号如式（13）和式（14）所示。

图3 OFDM-IDMA系统框图Fig.3 OFDM-IDMA system block diagram

在不考虑FFT 的情况下，OFDM-IDMA 的复杂度为O(NitNcK)，其中Nit为迭代次数，Nc为载波数，K为用户数。即OFDM-IDMA 的算法复杂度与迭代次数Nit，载波数Nc以及用户数K线性相关。

4 仿真结果

4.1 信干比分析

本节使用MATLAB 进行仿真，分析了目标距离对信干比的影响，以及低SIR对模糊函数的影响，验证了IRCS 同频干扰抑制的必要性。本次仿真中主要考虑IRCS 特有的来自通信信号对雷达回波的干扰，因此，假设IRCS中有一个雷达节点，两个通信节点，且三个节点的发射功率、发射天线增益和接收天线增益相同。参考LTE 中宏基站的相关参数，设置IRCS 中每个基站的覆盖距离为1000 m，干扰距离为1732 m，目标散射截面积为1 m2。

首先分析了IRCS 中，目标距离对SIR 的影响。为方便仿真，将边长为1000 m 的正六边形近似为半径为1000 m 的圆。仿真了不同距离下的信干扰比分布。仿真时，设置距离间隔为50 m，角度间隔为6°，得到的仿真结果如图4 所示。图4 中的原点表示雷达所在位置，整个平面表示目标可能出现的位置，横轴表示水平坐标，纵轴表示垂直坐标，颜色表示信干比。从图4 可知，目标距离雷达越远，SIR 越低，反之SIR 越高。当目标距离大于330 m 时，信干扰比低于−50 dB。假设目标一体化节点所需探测的最远距离为1000 m，且目标位置在整个圆内均匀分布，则在雷达探测过程中，存在约89.11%的概率，信干扰比小于−50 dB。IRCS 同频干扰导致SIR 降低，且目标距离越远，SIR越低。

图4 信干扰比示意图Fig.4 Signal-to-interference ratio diagram

然后基于OFDM 一体化信号，仿真分析了SIR对雷达模糊函数的影响，仿真参数设置如表1所示。计算可知，距离分辨率ΔR为7.5 m，速度分辨率Δv为4.5776 m/s。设置目标相对于雷达的距离为560 m，速度为15 m/s，即目标距离约为75ΔR，速度约为3Δv。

表1 仿真参数表Tab.1 Simulation parameters

基于上述参数，仿真了SIR=−50 dB 和干扰不存在时的雷达模糊函数，仿真结果如图5所示。其中，图5（a）为SIR=−50 dB 的速度-距离图，图5（b）为干扰不存在时的速度-距离图。其中，默认距离的单位为ΔR，速度的单位为Δv，归一化幅度的单位为dB。从图5 可以看出，干扰存在时，SIR 较低，干扰导致模糊函数噪声基底抬高，目标完全被干扰湮没，无法检测出目标，影响目标参数估计。

图5 不同SIR下的雷达模糊函数图Fig.5 Radar ambiguity function with different SIR

综上所述，当目标距离越大，一体化节点的SIR越大。IRCS 同频干扰的存在会导致SIR 降低，噪声基底抬高，无法检测出目标等问题。因此需开展基于OFDM的IRCS同频干扰研究。

4.2 同频干扰抑制算法验证

本节利用MATLAB，对所提基于OFDM-IDMA的IRCS 同频干扰抑制方法进行仿真验证和性能分析。仿真参数设置仍如表1所示，距离分辨率ΔR为7.5 m，速度分辨率Δv为4.5776 m/s。本次仿真扩频长度为4，采用卷积编码，编码速率为1/2，生成多项式为（23，35）8。仿真共设置了七个IRCS 节点，其中一个记作雷达节点，另外六个记作通信节点。每个通信节点设置一条直达波和四条静杂波，通信节点静杂波的路径长度在[230ΔR，400ΔR]中随机产生。雷达节点共设置四条静杂波，雷达静杂波距雷达节点的距离为10ΔR、15ΔR、27ΔR和40ΔR。同时设置三个目标，目标相对于雷达的距离设为｛320 m，320 m，560 m｝，速度为｛15 m/s，40 m/s，40 m/s｝，即目标距离约为{43ΔR，43ΔR，75ΔR}，速度约为{3Δv，9Δv，9Δv}。同时设置目标回波功率为1，通信信号的功率为50 dB，通信直达波与四条静杂波的幅度比值为1∶0.9∶0.6∶0.3∶0.1。基于上述参数，仿真验证了基于OFDM-IDMA 的IRCS 同频干扰算法性能。

首先，仿真了干扰抑制前的模糊函数。通过将干扰抑制前的接收信号与雷达参考信号二维互相关，得到的仿真结果如图6所示。其中，图6（a）为三维模糊函数图的速度-距离视图，其横坐标表示速度，纵坐标表示距离，颜色表示归一化幅度；图6（b）为三维模糊函数图在v=0时的距离剖面图，其横坐标表示距离，纵坐标表示归一化幅度。从图6 可以看出，干扰抑制前，受通信节点发送信号和雷达静杂波的影响，模糊函数噪声基底抬高，无法准确识别出目标。此时模糊函数中有四个峰值出现，四个峰值出现的位置分别为10ΔR、15ΔR、27ΔR和40ΔR，四个峰值代表四条不同的雷达静杂波。

图6 干扰抑制前的模糊函数图Fig.6 Ambiguity function before interference suppression

这是因为与目标回波相比，通信信号和静杂波的功率较大，目标被完全湮没。由于雷达静杂波与通信信号的功率相当，且通信信号与雷达信号线性无关，所以可以识别出雷达静杂波。

其次，仿真了雷达静杂波抑制后的模糊函数图。将雷达静杂波消除后的信号与雷达参考信号进行二维互相关，得到的模糊函数图如图7 所示。图7（a）为三维模糊函数图的速度-距离视图，其横坐标表示速度，纵坐标表示距离，颜色表示归一化幅度；图7（b）为三维模糊函数图在v=0 处的距离剖面图。从图7 可以看出，模糊函数无明显峰值。这是因为经过雷达静杂波抑制后，接收信号主要包括雷达目标回波、通信直达波和静杂波。通信直达波和静杂波与雷达参考信号线性无关，因而不会产生峰值。雷达目标回波功率相对于通信信号功率较低，所以被完全湮没，也没有产生峰值。综上所述，图7中无明显峰值出现。

图7 雷达静杂波抑制后的模糊函数图Fig.7 Ambiguity function after radar static clutter suppression

接着，仿真了不同信噪比（Signal-to-Noise Ra⁃tio，SNR）下，通信信号分离的误码率。利用OFDMIDMA 算法，对雷达静杂波抑制后的信号实现通信信号分离。OFDM-IDMA 算法的误码率（Bit Error Ratio，BER）会影响干扰抑制和目标参数检测的性能。因此仿真分析了OFDM-IDMA 的BER 随SNR的变化曲线，仿真结果如图8 所示。从图8 可以看出，随着SNR 的增大，OFDM-IDMA 算法的误码率逐渐降低。当SNR=6 dB，迭代次数大于等于5 时，误码率低于10-5。同时，从图8 可以看出，当迭代次数小于等于5时，迭代次数越多，误码率越低。当迭代次数大于5 时，随着迭代系数的增加，SNR-BER 曲线逐渐收敛。迭代次数越多，算法的误码率越低，但计算复杂度越大，因此，综合考虑复杂度和误码率性能，宜采用10次迭代。

图8 不同迭代次数下的SNR-BER曲线Fig.8 SNR-BER curves under different iterations

然后，仿真了不同BER 对噪声基底和干扰抑制的影响。OFDM-IDMA 的误码率会影响同频干扰抑制性能。考虑不同误码率下的干扰抑制比，干扰抑制比是指抑制前信号的能量/抑制后的信号能量，干扰抑制比随误码率的变化曲线如图9（a）所示。同时仿真了干扰抑制前和干扰抑制后模糊函数的噪声基底随误码率的变化曲线，仿真结果如图9（b）所示。从图9可以看出，随着误码率的增加，抑制后信号的噪声基底逐渐抬高，干扰抑制比逐渐降低。当误码率较低时，抑制后的信号噪声基底较低，干扰抑制比较高，干扰能量残存较少，可以有效抑制干扰。反之，当误码率较大时，抑制后的噪声基底较高，干扰抑制比较低，干扰能量残留较多，依然会严重影响目标探测性能。

图9 误码率对干扰抑制性能的影响Fig.9 Influence of bit error rate on interference suppression

最后，仿真分析了基于干扰重构的干扰消除技术的抑制性能。采用迭代次数为10的OFDM-IDMA算法，对雷达静杂波抑制后的信号进行通信信号分离。此时目标回波功率较小，OFDM-IDMA 算法的信噪比较高，仿真得到的误码率为7.6 × 10-6，可以比较准确地重构出通信信号。再使用基于干扰重构的干扰消除技术将通信干扰消除。最后，仿真了通信干扰抑制后的模糊函数，仿真结果如图10 所示。图10（a）为三维模糊函数图的速度-距离视图，其横坐标表示速度，纵坐标表示距离，颜色表示归一化幅度；图10（b）为三维模糊函数图在R=43ΔR处的速度剖面图和v=9Δv处的距离剖面图。图10中噪声基底约为−50 dB，可以明显看到三个峰值，第一个峰值出现的距离为43ΔR，速度为3Δv，第二个峰值出现的距离为43ΔR，速度为9Δv，第三个峰值出现的距离为75ΔR，速度为9Δv。三个峰值出现的距离与速度与设置的目标相同。此时，通信干扰和雷达静杂波均被抑制，将干扰抑制后的信号与雷达参考信号二维互相关，可以准确检测到三个目标。验证了基于OFDM-IDMA 的IRCS 同频干扰抑制算法的可行性。

图10 通信干扰抑制后的模糊函数图Fig.10 Ambiguity function after communication interference suppression

5 结论

本文开展了OFDM 雷达通信一体化研究，提出了一种基于OFDM-IDMA 的同频干扰抑制算法。首先给出了雷达通信一体化同频干扰的系统模型和信号模型。然后从回波信号信干比分析了IRCS 同频干扰特性，推导了回波信号信干比的理论表达式，理论结果表明，回波信号信干比随干扰距离的增大而增大，随干扰发射功率的增大而减小。仿真结果表明，干扰导致信干比降低、模糊函数噪声基底抬高，有效验证了IRCS 同频干扰抑制的必要性。接着将OFDM-IDMA 算法和基于干扰重构的干扰消除算法相结合，提出了基于OFDM-IDMA 的IRCS 同频干扰抑制算法。所提算法通过不同的交织方式区分不同的IRCS节点的信号，同时利用基于干扰重构的干扰消除算法实现干扰抑制。仿真结果表明，此算法可以在保证频率利用率的条件下，较为准确地重构干扰信号，有效抑制了IRCS 同频干扰，证明了所提算法的有效性。