基于滤波器组多载波梳状谱的雷达通信一体化信号技术

王 杰 裴泽琳 陈 军 梁兴东 李焱磊 陈龙永

（1.南京信息工程大学电子与信息工程学院，江苏南京 210044；2.中国科学院空天信息创新研究院，北京 100190；3.微波成像技术国家级重点实验室，北京 100190）

1 引言

早在上个世纪60年代，就有学者提出了雷达通信一体化的概念。早期关于雷达通信一体化的研究主要集中在雷达与通信的发射机、接收机、天线等硬件的共享上［1］。近年来，欧美、日韩等军事强国已在通道、孔径、处理、显示与控制等层面上实现了雷达和通信的共享，并进一步将其研究重点推向了信号一体化［2］。如何设计一种信号，使之在满足通信信息高速传输要求的同时，又能较好地实现雷达探测功能，是当前迫切需要解决的核心技术难点［3］。

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术凭借其载波调制灵活、频谱效率高等优点在一体化信号的设计方面得到了广泛关注［4］。其中，OFDM梳状谱技术是备选一体化技术之一［5］。然而，OFDM技术也存在一些不足。具体而言，OFDM 对频偏非常敏感，容易受到较为严重的载波间干扰。这种干扰在OFDM梳状谱框架下主要体现为雷达和通信间的相互干扰，会大幅降低雷达和通信性能［6］。与之相比，滤波器组多载波（Filterbank multicarrier，FBMC）技术具有更高的多普勒容限，且不需要循环前缀（Cyclic Prefix，CP），已成为雷达通信一体化信号的重要潜在技术之一［7-8］。目前，国内外对于利用FBMC技术实现雷达通信一体化的研究相对较少。较典型的方案是利用FBMC通信信号实现雷达探测或成像功能［9-11］。然而通信信息具有很强的随机性，会在脉压结果中引入过高的旁瓣。因此，本文主旨思想是，在FBMC 框架下，从子载波复用的角度，设计FBMC梳状谱信号，使雷达和通信在子载波维度相对独立，进而兼具良好的雷达探测与通信性能。但是FBMC原型滤波器在子载波上存在固定的虚数干扰，势必会对一体化信号的信道估计产生影响。该问题是FBMC技术的共性问题。

近年来，有不少国内外学者对FBMC 系统中信道估计算法展开了广泛的研究。如文献［12-14］提出了基于干扰利用（Interference Approximation Method，IAM）的信道估计算法及改进型的IAM 算法。文献［15］提出了一种基于干扰消除（Interference Elimina⁃tion Method，IEM）的算法。以上算法的缺点在于至少需要三个FBMC 符号来构造块状前导序列，且仅仅考虑一阶时频点的干扰。文献［16］提出了一种基于导频对算法（Pair of Pilots，POP），该算法虽然只占用了两个FBMC 符号，但是并未考虑到噪声对信道估计的影响，在实际的无线通信系统中性能会受到一定限制。针对以上导频设计的不足，本文提出了一种新的块状导频结构设计方法。核心思想是，通过利用导频周围一阶时频点的已知干扰增大导频点功率，提升导频抗噪性能，并在导频点数据左侧放置辅助导频（Auxiliary Pilot，AP），用以消除高阶时频点的干扰。此外，在应对快时变信道时，本文联合块状导频与离散的梳状chirp谱进行信道估计，用以保障高动态应用场景下的通信性能。

本文结构如下：第2 节第一部分介绍了FBMC原理；第二部分介绍了FBMC 梳状谱一体化信号的设计方法，其中包括雷达信号结构设计与通信导频结构设计方法；第3 节完成了FBMC 梳状谱信号的仿真验证，并与OFDM 梳状谱形成了对比；第4节对本文进行了总结。

2 基于FBMC梳状谱的一体化技术

2.1 FBMC原理

与OFDM 类似，FBMC 波形是多载波技术，以频分复用为基础，在相互正交的子载波上实现信息的调制［17］。与OFDM 不同的是，FBMC 的子载波仅在实数域正交。在频域，FBMC 的子载波旁瓣远远低于OFDM 子载波的旁瓣。换言之，FBMC 带外辐射低，对频偏不敏感。

为了降低频域子载波的旁瓣，FBMC 采用进行特殊设计的原型滤波器［9］，例如常用的PHYDYAS原型滤波器。图1（a）展示了OFDM 子载波频域响应，图1（b）展示了重叠因子为4 时，FBMC 原型滤波器的频域响应。从图中可以看出，相较于OFDM 子载波频域响应，原型滤波器的频域子载波旁瓣被抑制，带外干扰非常小。

图1 OFDM与FBMC频域响应图Fig.1 Frequency domain response diagram of OFDM and FBMC

由于原型滤波器具有优秀的带外抑制能力，FBMC 的非相邻子载波之间是没有能量重叠的。只有相邻子载波间存在干扰，且干扰的时域响应为［18］：

其中，干扰时域响应的相位因子为

且K为重叠因子，Gk为与K有关的常数，T为FBMC的符号周期。

依据相位因子可知，干扰的时域响应函数的实部会在t等于奇数倍T/2 时为0，虚部会在t等于偶数倍T/2 时为0。换言之，g(t)的实部与虚部的零点将以T/2 为间隔交替出现，这使得FBMC 系统需要采用特殊的调制方式来抑制相邻子载波间的干扰。

在FBMC 系统中，所采用的调制方式为偏移正交幅度（Offset Quadrature Amplitude Modulation，OQAM）调制。OQAM 预处理分为两步：首先将一个复数信号实部和虚部拆分开，然后在实部和虚部间延时半个符号周期进行传输。如图2 所示，这种传输方式可以有效抑制相邻子载波之间的干扰。由于FBMC-OQAM 在每个子载波上传递的是实值的信号，而OFDM 传递的是复数信号，因此FBMCOQAM 的编码效率是OFDM 的一半，但是其符号速率是OFDM 的两倍，所以可以达到和OFDM 相同的数据传输速率。

图2 OQAM调制示意图Fig.2 OQAM modulation

2.2 基于FBMC梳状谱的一体化信号设计思路

本文充分利用子载波间的实正交性，首先将雷达chirp 信号离散频谱值调制到FBMC 信号的第1，M+1，2M+1，...，(a-1) ⋅M+1（其中M为雷达相邻频点的间隔数，a为雷达chirp 占用的子载波数目）个子载波上，其次将OQAM 调制后的通信实数据调制到剩余子载波上，进而构成子载波复用信号。FBMC梳状谱信号的时域模型如式（3）所示

式（4）中，aM为子载波数，N为符号数，g(k)表示长度为K×aM的原型滤波器，bm，n为第n个符号上的第m个子载波的权值。相位因子πmn+(m+n)使一体化信号在时域和频域上实虚交错。g(k)同相位2πm(k-)/(aM)构成滤波器组。式（5）中，rm，n为雷达chirp 离散频谱值，cm，n为通信离散频谱值（m，n分别表示子载波和符号位置，cm，n为实数，rm，n为复数）。

若令

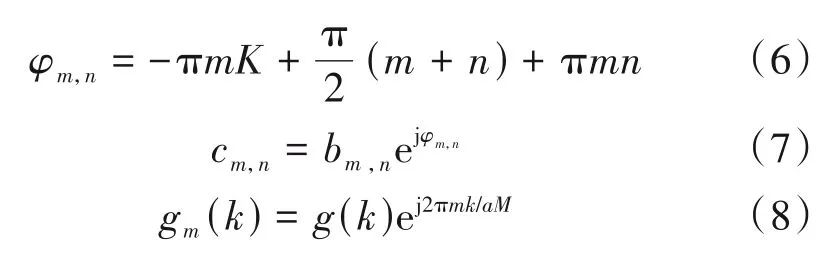
则式（4）可简化为

在接收端，通常利用M/2 间隔、KM长度的滑窗对接收到的信号进行处理，并通过串并转换得到多个长度为KM的采样序列。

理想情况下经过滑窗得到的信号为rn(k)=sn(k)，与原型滤波器的共轭相乘可得

将rn(k)=sn(k)代入式（10），可得在第p个子载波上，第q个符号处的解调信号为

其 中，当(p，q)=(m，n) 时，δ(m，p)，(n，q)=1；当（p，q）≠（m，n）时，该项为纯虚数，如表1所示。

再将Rp，q进行取实部操作，即可恢复出原信号。

FBMC 梳状谱信号的调制解调框图如图3 所示。在调制端，一体化系统将编码、数字调制、串并转换、实虚分离后的通信码元和雷达chirp 数据组合。经原型滤波器、重叠求和、D/A 转换后，得到FBMC 梳状谱时域信号，并通过发射机发射。在接收端，雷达处理系统将接收的回波信号经A/D转换、滑窗接收、与原型滤波器的共轭相乘后，提取出调制在该信号中的雷达chirp数据，并进行雷达信号处理，从而得到待测目标信息。通信接收端将接收的一体化信号经A/D转换、滑窗接收，与原型滤波器共轭相乘后，提取出调制在该信号中的通信码元，并对通信码元进行信道估计和信道均衡，最后经数字解调、解码后得到通信数据。

图3 基于FBMC梳状谱信号调制解调框图Fig.3 Block diagram of modulation and demodulation based on FBMC comb spectrum signal

实际上，依据FBMC梳状谱调制解调原理可知，无论是雷达子载波还是通信子载波数据，都会受到原型滤波器的固有虚部干扰影响。对于雷达chirp信号来说，固有干扰会使得雷达匹配滤波的旁瓣升高，影响雷达探测性能。对于通信信号来说，固有虚部干扰会与信道响应叠加在一起，进而降低通信信道估计精度。下面将重点围绕抑制虚部干扰，对FBMC 梳状谱框架下的雷达信号结构和通信导频结构进行优化设计。

2.2.1 FBMC梳状谱信号中的chirp结构

传统的FBMC 结构采用OQAM 调制方式，将信号的实虚部拆分，并将虚部延时半个符号周期发送。对于雷达chirp信号来说，若将虚部延时半个周期发送，则雷达实部和虚部间的时延过大，从而影响探测性能。雷达信号若是不采用实虚分离，则会对周围通信数据产生实数干扰，进而大幅增加通信误码率。结合表1原型滤波器干扰因子的分布特点可知，特定时频点(p，q)受到的干扰主要来自于上下相邻子载波和左右多阶符号。因此本文在雷达chirp复信号的上下子载波处放置空白保护间隔，以此隔绝雷达信号对通信信号的影响，并在相邻符号间放置空白间隔，来隔绝符号间的雷达信号干扰。该结构示意图如图4所示。

图4 FBMC梳状谱信号中chirp信号结构Fig.4 Chirp signal structure in FBMC comb spectrum signal

表1 干扰因子Tab.1 Interference factor table

2.2.2 FBMC梳状谱信号中的通信导频结构

当存在信道影响时，通信节点接收到的数据可表示为

式（13）中，Hp，q为频域信道响应，η为高斯白噪声，Ip，q为时频点(p，q)周围数据经过信道对(p，q)处产生的干扰，其值为

假设信道是缓慢变化的，即Hm，n≈Hp，q，那么(p，q)处的信道估计值如式（17）

由式（17）可以看出，等效导频dp，q的模值越大，系统的抗噪性能越好。传统增大dp，q的导频结构有三种，分别为干扰利用-R（IAM-R）、干扰利用-I（IAM-I）、干扰利用-E-C（IAM-E-C）。以上三种导频结构图如图5（a）、图5（b）和图5（c）所示。

图5 传统干扰利用算法导频结构Fig.5 Pilot structure of traditional jamming utilization algorithm

图5（a）为IAM-R 算法［12］的导频结构图，导频序列由三个符号组成，中间符号为导频序列，取值依次为（1，1，-1，-1）。左右两列的导频符号值为0，对中间列导频起到保护的作用。图5（b）为IAM-I算法［13］的导频结构图。IAM-I算法为IAM-R算法的改进，通过在中间导频列引入虚数来增大dp，q的模值。考虑到左右两列的导频符号还可以做进一步的改进以便使等效导频符号dp，q的能量再一次的增强，文献［14］提出了IAM-E-C算法，导频结构如图5（c）所示。

然而，上述导频结构算法存在一个共同的问题：只考虑了一阶干扰对导频点数据的影响。基于此，本文提出了一种新的导频结构设计，即IAM-AP 结构。其核心思想为：利用导频周围一阶时频点数据产生的干扰增大dp，q的模值，用以提升系统的抗噪性能；利用辅助导频消除高阶时频点的干扰，从而提升信道估计准确度。IAM-AP结构图如图6所示。

图6 IAM-AP算法导频结构Fig.6 IAM-AP algorithm pilot structure

如图6 所示，IAM-AP 算法利用两个FBMC 符号构造前导序列。在第二个符号上，导频数据间隔放置，其值依次为（1，-1）。在导频数据左侧添加辅助导频，用以消除高阶时频点数据对导频点数据的干扰。结合表1 中干扰因子的特性，可在第一个符号上除辅助导频外的其他子载波位置放置数据1，在第二个符号除导频数据外的其他子载波位置上间隔放置（j，-j）来增大导频点的功率。

结合图6，导频周围一阶时频点（除辅助导频位置）产生的干扰为

设辅助导频点的数值为bp，q-1，则导频点处受到一体化数据产生的高阶干扰和辅助导频产生的干扰为

为了消除一体化数据产生的高阶干扰，需要设计辅助导频的值，使=0。

辅助导频点的数值bp，q-1在=0时取值如下：

式（20）确定了辅助导频的取值，还需要确定辅助导频的位置。依据式（20）可知，δ(p，p)，(q，q-1)的值越小，辅助导频的值越大，这会使传输信号的峰均比增加。为了不提高传输信号的峰均比，一般会选取δ(p，p)，(q，q-1)较大的位置放置辅助导频。由表1 可知，对于本文采用的PHYDYAS 原型滤波器来说，在导频点上下左右四个相邻位置处，左侧或右侧的干扰因子最大，因此本文在进行导频结构设计时将辅助导频放在导频点数据的左侧。

由表2 可知，在传统的导频结构中，IAM-E-C 的dp，q值最大，抗噪性能最好。本文设计的导频结构等 效导频dp，q的模 值介于IAM-E-C 与IAM-I 之 间。因此，在低信噪比条件下，本文导频结构对信道响应估计的精度略低于IAM-E-C 算法。但是传统导频结构设计都只考虑导频周围一阶时频点对导频数据的干扰，未考虑高阶干扰。当周围数据对导频点产生的虚部干扰影响大于噪声对导频点数据的影响时，只提高信噪比就无法改善系统的通信性能。此外，传统导频结构导频开销过大（都占用了三个FBMC 符号），在一定程度上浪费了通信资源。而本文提出的导频结构既节省了导频开销，又综合考虑了一阶及高阶虚部干扰，可在高信噪比条件下获得优越的通信性能。

表2 不同导频结构的up，q及dp，q值Tab.2 up，q and dp，q of different pilot structures

为了验证IAM-AP 导频结构的性能，本文在不同的信道下进行了仿真对比验证，其中，信号带宽为100 MHz，通信调制方式为16QAM，采样率为120 MHz，子载波个数为9600。仿真信道为步行ITU_PA 信道和车载ITU_VA 信道，信道结构如表3所示。

表3 ITU_PA和ITU_VA信道参数Tab.3 ITU_PA and ITU_VA channel parameters

图7（a）和7（b）为采用不同导频结构在ITU_PA和ITU_VA 信道下误码率仿真曲线。由仿真图可以看出，在信噪比较低时，IAM-E-C 算法抗噪性能较好，误码率较低。但随着信噪比增加，高阶干扰的影响会逐步大于噪声的影响。此时，IAM-E-C 算法无法改善通信性能。与之相比，虽然本文提出的导频结构在低信噪比时误码率略高于IAM-E-C 算法，但是节省了一列导频资源。当系统的信噪比超过20 dB 时，本文设计的导频结构对于一体化系统的通信性能有显著的提升。

图7 不同导频结构的FBMC梳状谱一体化信号在不同信道下误码率Fig.7 Ber of FBMC comb spectrum integrated signals with different pilot structures in different channels

结合雷达信号结构和通信导频结构的设计方案，可得本文一体化信号的时频特性图如图8所示。对于FBMC 梳状谱信号来说，前两个符号作为块状导频序列，后续符号用来传输一体化数据。当信道在时域上变化较快时，可将雷达信号当成通信离散导频，与本文设计的块状导频序列结合进行信道估计，从而进一步提升信道估计的准确度。

图8 FBMC梳状谱一体化信号时频资源图Fig.8 FBMC comb spectrum integrated signal time-frequency resource map

3 仿真与分析

3.1 仿真场景

图9 为雷达通信一体化信号仿真场景。节点A为雷达通信一体化系统。一体化系统在与目标1通信的同时，对波束内目标进行探测。节点A和目标1之间的传播信道为单直射径莱斯信道，该信道的差分时延为0 ns，功率为0 dB，多普勒频移为1250 Hz。

图9 雷达通信一体化信号仿真场景图Fig.9 Radar communication integrated signal simulation scene

3.2 参数设置

场景中设置4个目标，目标对应的距离、速度信息如表4 所示。一体化信号的总带宽为100 MHz，其中，雷达和通信等效带宽均为100 MHz。

表4 一体化系统的仿真参数Tab.4 Simulation parameters of integrated system

3.3 结果分析

图10（a）、（b）分别为FBMC 梳状谱信号的雷达点扩展函数图和雷达chirp 信号的模糊函数图。由于本文设计的FBMC 梳状谱信号将雷达chirp 信号离散频谱值均匀调制在子载波上，并在接收端提取chirp 频点进行雷达探测，因此其点扩展函数近似sinc 函数，模糊函数图同经典的chirp 信号的模糊函数图一致。根据仿真结果可知距离分辨率为1.32 m，峰值旁瓣比（Peak Side Lobe Ratio，PSLR）为-13.33 dB，积分旁瓣比为（Integration Side Lobe Ratio，ISLR）为-9.92 dB。由此可见，本文设计的FBMC梳状谱信号具有良好的模糊函数特性。

图10 雷达点扩展函数与模糊函数图Fig.10 Radar point spread function and ambiguity function diagram

为了验证FBMC 梳状谱技术的有效性，本文在相同的仿真参数下，对OFDM梳状谱技术与FBMC梳状谱技术进行了仿真对比试验。仿真结果如图11、图12、图13所示。

图11（a）、（b）分别为通信接收端接收到的OFDM梳状谱与FBMC 梳状谱通信误码率和星座映射图。从该图可以看出，在高速移动的场景下，OFDM 梳状谱信号的误码率较高，为10−2。而FBMC梳状谱误码率可以达到10−6数量级，满足通信系统的可靠性要求。图12（a）、（b）分别为节点A利用OFDM梳状谱信号和FBMC 梳状谱信号获取的雷达探测PD（Pulse Doppler）图。图（a）中显示了四个动目标，其距离和速度分别为（300 m，78.13 m/s）、（350 m，28.08 m/s）、（500 m，-62.26 m/s）、（600 m，47.61 m/s），测速误差分别为15.63 m/s、3.08 m/s、12.26 m/s、10.11 m/s。图（b）中显示了四个动目标，其距离和速度分别为（300 m，62.26 m/s），（350 m，25.63 m/s），（500 m，-50.05 m/s），（600 m，37.84 m/s），测速误差分别为0.24 m/s、0.63 m/s、0.05 m/s、0.34 m/s。对比图（a）和图（b）可以看出，在多普勒频偏较高时，FBMC 梳状谱信号具备更好的雷达探测性能。

图11 本文共享信号与OFDM信号在不同信噪比下的误码率比较Fig.11 Comparison of bit error rate of shared signal and OFDM signal under different signal-to-noise ratios

图12 不同距离不同速度下的估计误差比较Fig.12 Comparison of estimation errors at different distances and speeds

OFDM 梳状谱信号对频偏较为敏感，这是因为多普勒频偏会改变子载波之间的相对位置，使每个子载波的旁瓣在其他子载波峰值处的分量不再为零，进而导致雷达通信间互干扰。且互干扰能量对雷达和通信的影响主要体现为信干比。频偏越大，干扰越强，雷达和通信的性能越差。与之相比，若多普勒频偏改变了FBMC 子载波之间相对位置关系，则可分为两种情况讨论：首先，由于子载波的主瓣较宽，相邻子载波之间仍然存在相互干扰；其次，由于子载波的旁瓣近似为零，非相邻子载波之间的干扰可以忽略。对于相邻子载波间干扰，本文采用了空白间隔隔绝。采用空白间隔会使得FBMC梳状谱信号的频谱利用效率相较于OFDM 梳状谱信号下降2.5/M（M为雷达相邻频点的间隔数，本文仿真中设置为10）。本文采用互干扰能量为指标，来衡量一体化性能。图13为OFDM梳状谱信号与FBMC梳状谱信号在不同频偏下的雷达通信互干扰能量对比图。从图中可以看出，与OFDM 梳状谱信号相比，FBMC 梳状谱信号具备更高的多普勒容限。在相同的归一化多普勒频偏下，FBMC 梳状谱信号子载波间的互干扰能量比OFDM 梳状谱信号子载波间的互干扰能量低了至少30 dB。因此，可从仿真结果看出，FBMC 梳状谱信号具备实现雷达与通信同时、同空域、高效共享频谱的可行性。此外，FBMC 梳状谱信号还具备较高的多普勒容限，满足高动态应用需求。

图13 OFDM梳状谱与FBMC梳状谱在不同频偏下雷达通信间互干扰对比图Fig.13 Comparison diagram of mutual interference between OFDM comb spectrum and FBMC comb spectrum under different frequency offset

4 结论

OFDM 是较为经典的多载波技术，但OFDM技术存在子载波频域旁瓣高、对频率偏移敏感等缺点，实用价值相对有限。随着通信技术的发展，FBMC由于其旁瓣低、多普勒容限高等优点受到了更多关注。因此，本文在FBMC框架下，从进一步挖掘、拓展和利用时频域子载波自由度的角度，提出了能够同时实现雷达探测定位功能和高速通信数据传输功能的FBMC梳状谱信号技术。其次，本文分析了FBMC系统中固有虚部干扰引起通信信道估计精度下降的问题，并进一步提出了融合辅助导频和干扰利用的前导序列设计方法。与此同时，在应对快时变信道时，雷达chirp信号可用作通信导频，提升信道估计精度，进而保障了优良的通信性能。仿真结果表明，本文设计的前导序列在信噪比较高时能有效提升一体化系统的通信性能。相较于OFDM梳状谱信号，在高速移动的场景下，本文设计的FBMC梳状谱信号具备更好的雷达探测性能和通信性能。此外，由于原型滤波器的使用会使得FBMC系统的计算复杂度大幅上升。而本文采用空白间隔隔绝虚部干扰的方式会造成频谱资源利用率的下降。因此，可将降低FBMC梳状谱信号的计算复杂度和提升频谱资源利用率作为下一步研究的重点。