工程建设与财政平衡决策问题的优化分析

刘寒冰LIU Han-bing；段兆凡DUAN Zhao-fan；张宇轩ZHANG Yu-xuan；陈宇轩CHEN Yu-xuan；张书源ZHANG Shu-yuan

（山东科技大学，济南 250000）

0 引言

近年来，随着大数据技术的急剧发展，数学建模逐渐应用到工程建设等领域，并发挥着举足轻重的作用，其不仅克服了传统数据分析与手工建模的低效率弊端，还在一定程度上引用各种优化算法使得相关工程建设更加高效，达到多层级优化的作用。胡运权[1]在其著作中总结了运筹学建模的多种方法，通过多种实际样例论述了运筹学在社会生产方面的重要性；梁爽[2]结合已知数学模型，通过Lingdo、Mathematical等计算机软件对相关问题进行求解并分析；王莎娜[3]针对洛阳豫西北地区水资源规划配置问题，运用Matlab的线性规划算法对该地区水资源进行了合理划分；陈士成[4]等人通过分析Excel的内置规划求解方法，论证了该求解方法的简洁性和实用性。该工程建设与财政平衡问题模拟了现实中市政可能会遇到的各种情况，并基于运筹学建立相关模型，利用Microsoft Excel中的规划求解功能进行特殊的单纯形法求解，以实现决策方的满意解。

1 规划求解方法概述

“规划求解”是Excel中的一个功能组件，求解方法包括非线性GRG求解、单纯线性规划求解和演化求解。借助该功能可求得工作表中某个单元格（或称为目标单元格）中表达式的最优值，其中表达式指的是单元格中的一系列值、单元格引用、名称或运算符的组合，可通过更改可变单元格生成新值，每个表达式总是以“=”开始。通过应用“规划求解”功能模块，决策者可以在目标单元格以及其余相关单元格得到详细的信息分析数据，最终结果将呈现于目标单元格中。

在运筹学中线性规划方法作为重要分支，其理论优化也是现代运筹学的主要核心内容，是量化分析的主要方式，对于基于一定约束条件下的决策者而言，通过对管理系统有限资源统筹规划就可为其提出最优选方法，从而达到最佳效益与经济性，所以，在企业产销、科研等管理过程中，把线性规划方法运用于其中，就形成了现代管理的主要手法。求解模板的制作主要解决四方面的问题：①在Word或其他软件中创建新文件，然后将规划模型的数据与数据分析简洁明了地呈现在该界面，以便下一步进行整理与调用；②合理规划模型数据参数的输入输出位置，一般可将参数分为绝对约束区、条件约束区、优先因子分流区、最优解输出区、最优值输出区、偏差变量输出区和文字注释区；③将模型相关数据输入对应的区域，并在模型中建立各个数据的映射关系，然后在规划求解功能模块构建约束关系，并且规定求解要求与方案；④在各个输出区显示迭代后的决策结果，如有需要可以选择输出“运算结果报告”、“敏感性报告”和“极限值报告”，从而使决策者更加直观的查阅底层数据。

2 问题描述

A市政府为完善基础设施建设，在3年内要进行以下5项工程的建设，其按重要性排序的工程项目及造价详见表1。

表1 市政工程项目及造价

A市政府的财政收入主要来自国有资产经营收益、行政性收费和规费收入。除了市政府的常规收入外，社会贷款和政府债券也是影响财政决策的因素。其中符号e表示市政府常规收入的三个部分，下标分别为1，2，3。而社会贷款也存在固定的上限值U，下标分别为11，12，13，其对应每年的利率为g。政府债券发行的上限值也为U，其下标分别为21，22，23。社会贷款一般在每年年初交付，还贷最长限制时间为1年，而每年期的政府债券在第二年会以r%的利率交付金额给持券人。A市政府为达到相关目标，应怎样合理规划这几年的投资方案。

3 设计与分析

设x1t为社会贷款额，x2t为政府债券发行量，yit为工程完工程度，也可以理解为投资比率，详见表2。

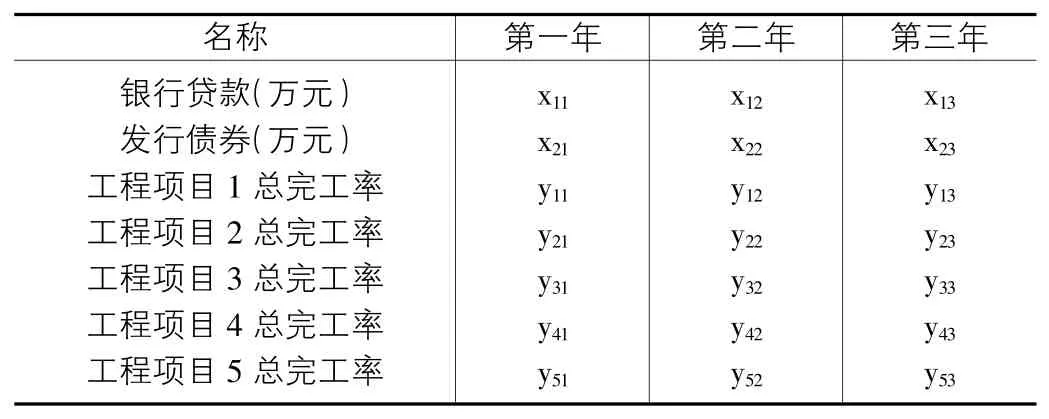
表2 各款项及完工率按年分配情况

为了满足财政平衡及其余相关平衡，我们将z0作为首年的平衡变量，接下来三年末所对应的平衡变量为z，下标分别对应各自的年份。

相关数据如图1所示。

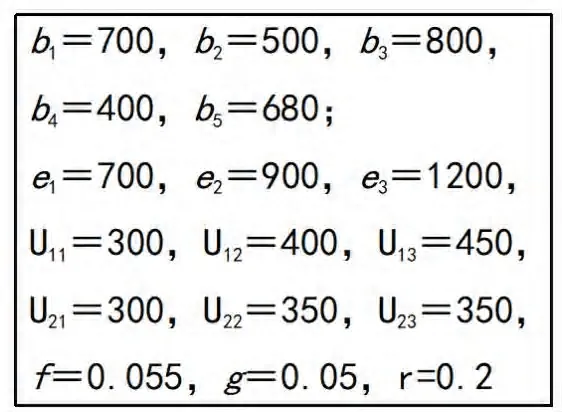
图1 各常量数值

3.1 贷款平衡约束（3个约束）

①设x1t为社会贷款额；

②变量都有上界限制的，把这些有上界约束的变量写成目标形式，其中只须引进负偏差变量njt

（其余展开式不再一一列出）

3.2 债券平衡约束（3个约束）

3.3 各项目每年完工率平衡约束（15个约束）

yit为工程完工程度，也可以理解为投资比率。

3.4 完工率平衡约束（5个约束）

3.5 三年财政平衡约束（3个约束，省略第一年初的平衡约束）

①我们将z0作为首年的平衡变量，接下来三年末所对应的平衡变量为z，下标分别对应各自的年份。②每年的平衡式实际上是个硬约束，是不包括偏差变量的，这在相关问题目标中也有所体现，所以我们将si作为松弛变量引入平衡式使等式平衡。③s4+k是负偏差变量，也可以当做松弛变量，d+5+k是正偏差变量，z0是首年年初的可使用财政金额，当z0的值为0时，“z0-s4=0”这条约束可忽略，故我们在配置平衡式时不将该式列入模型。zk是第k年年末所剩余的财政金额，该相应金额在第二年年初还可以继续使用，该条涉及到的所有变量值都是非负的。

3.6 三年中每年的财政平衡约束条件（3个约束）

根据财政平衡的意义，可以列出3年中每年的财政平衡约束条件，即

（此年社会贷款）+（此年政府债券发行量）+（此年政府财政收入）-（此年每项工程接纳的拨款）-（此年还贷数额）-（此年还债支出）-（此年还贷产生的利息）-（此年还债产生的利息）+（初始平衡）-（最终平衡）=0。

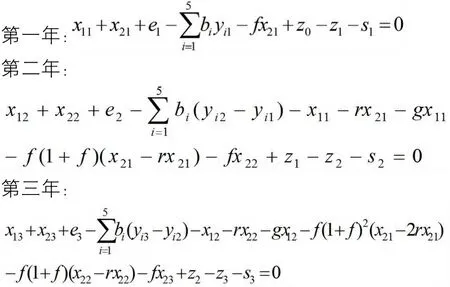
将e移到等号右边之后并展开得

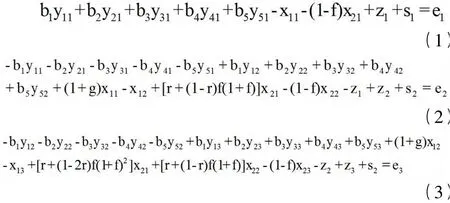
把常量代入后得

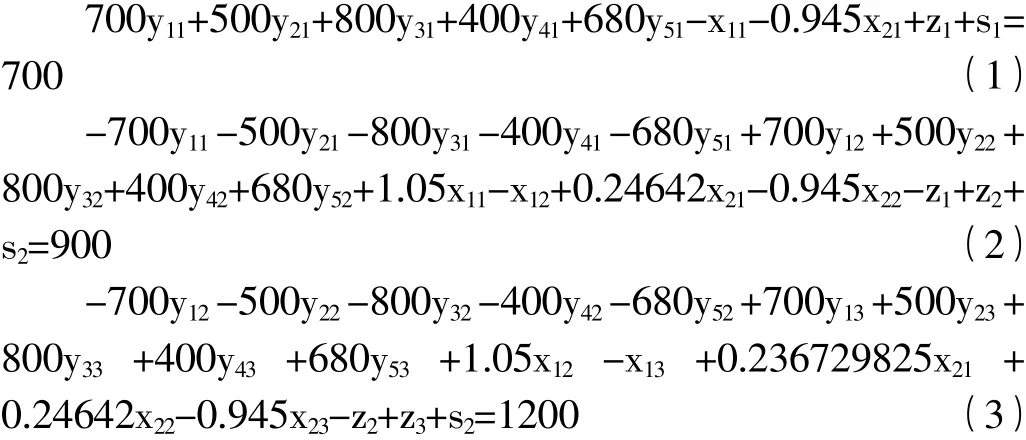
3.7 目标函数（共六级）

①为首先保证各年财政平衡，将硬约束设为1级目标，从而使相关约束条件的松弛变量的和为最小（P1）；

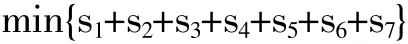
②希望通过社会贷款与政府债券发行的方式来解决此工程资金短缺的问题（P2）；

③按重点顺序加权，保证工程项目1，2优先完成；

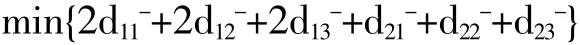
④按重点顺序加权，尽力赶工工程项目1，2，3；

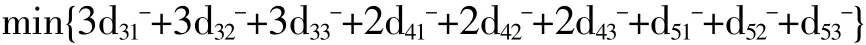
⑤尽量在3年内完成所有项目的建设；

⑥最小化每一年的政府财政平衡变量。

3.8 完整模型

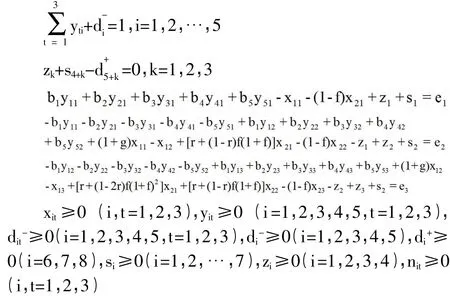
4 结果分析

①通过基础模型构建，我们可以简化出满足Excel内置“规划求解”方法的相关表达式，表达式以单元格为具体模块展开式分布，最终映射在功能模块的约束条目以及其他条目上。如图2所示，在设置完对应选项之后就可以进行求解，求解部分结果如图3所示——“规划求解找到一解，可满足所有的约束及最优状况”。

图2 Excel求解界面

图3 规划求解结果界面

经过多次迭代，新数据已经覆盖至原单元格，表3为该问题最终生成的满意解。

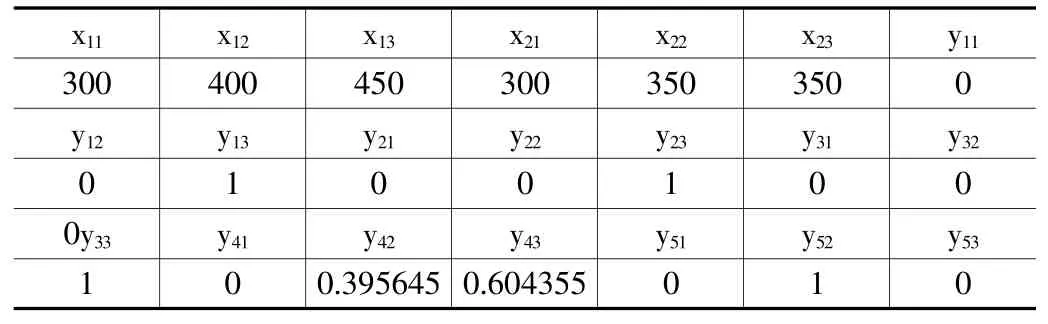
表3 迭代后的变量数据

②平衡表及优化分析。

表4为各年投资分布情况，图4为三年内银行贷款与发行债券条形图，图5为各年投资合计饼状图。

图4 三年内银行贷款与发行债券

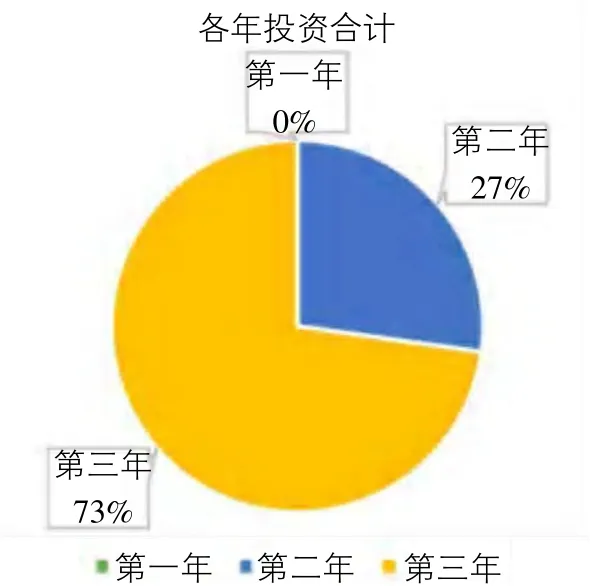
图5 各年投资合计

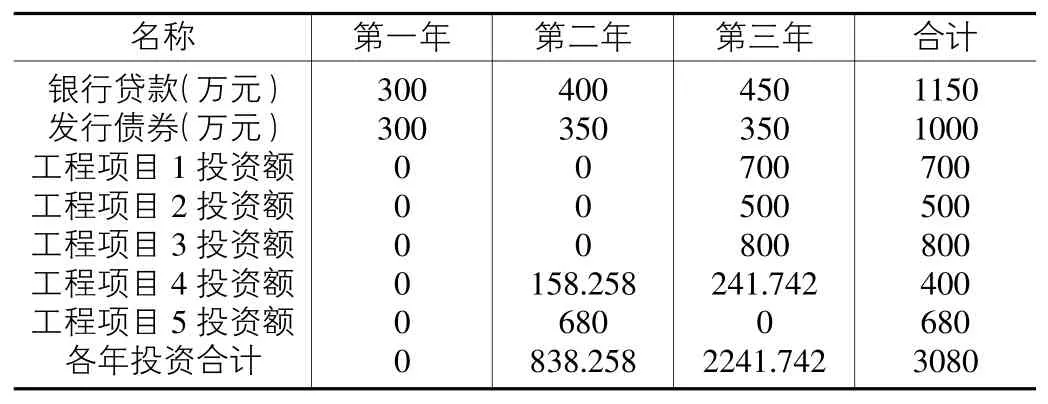
表4 各款项及完工率按年分配结果

工程需要资金总额3080万元，3年可用资金2800万元（e1+e2+e3），利息为（16.5+48.176+72.02541）万元。资金缺口：3080-2800+16.5+48.176+72.02541=416.7014万元。

可以根据实际情况任意选择优先目标，在本问题中可以继续调整优先目标的权系数来调整目标优先权重，可以

继续放大P1优先级尽量使财政达到平衡。

5 总结

针对某市政府在处理工程建设与财政平衡的问题，本文通过引入目标规划来处理多层级的优化，从而得到满意解。求解过程应用Microsoft Excel，避免了MATLAB处理复杂目标规划问题时出现的数据冗杂情况，使求解方案一目了然，最终通过代入模拟数据得到了该模型的满意解，明显在相关行业取得较优的决策。