一道平面向量最值问题的解法及其题源探究

南昌大学附属中学 (330047) 陈 松

平面向量中的最值问题，是一个热点问题，也是一个难点问题.其题型一般是根据所给的条件求某个量的最值，如向量的模、数量积、夹角及向量的系数等，解法灵活多样，变化多端，蕴含着数形结合、转化与化归等数学思想.本文以2022年天津市三模的一道平面向量最值题为例，探究该题在不同视角下的解法及其题源.

(2)向量兼具代数和几何双重特征，向量最值问题的解题方法较多，综合性强，由题意，本小题可从以下视角确解.

视角1坐标化

解法一：利用三角函数有界性求出最大值.

图1

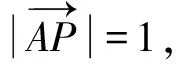
评注：注意到点M的为位置会根据点P的位置发生变化，可以通过考虑点P的轨迹方程寻找点M的轨迹，从而借助轨迹方程将问题转化为函数(或不等式)问题.

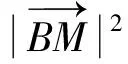
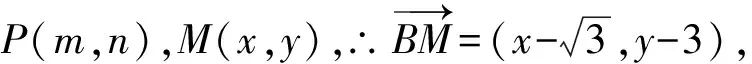
评注：利用相关点法找出点M的轨迹方程，然后将问题转化为一次(或二次)函数最值问题，这也是平面向量最值问题中常用解法.

视角2从几何性质出发

评注：本解法的关键在于找到点M的轨迹，将问题转化为曲线上的动点和曲线外一点的距离问题，所以将目标转移到寻找动点M的轨迹，问题.

视角3从基底和定义出发

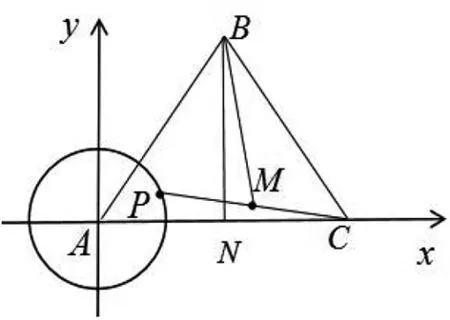
图2

评注：本解法的关键是选择合适的基向量，简化目标向量的运算，达到化繁为简，并运用适当的数学方法，如定义法、二次函数的思想、基本不等式的思想、三角函数思想等达到求解问题.

平面向量最值问题综合性强、灵活性大，我们从不同的视角寻找解题思路，往往可以得到不同的解决方案，恰是“横看成岭侧成峰，远近高低各不同”.万事万物总有源，开启寻源之旅，更有利于学生知识的串联，加深对知识本质的理解，培养学生解题和探究能力.