蝴蝶定理在圆锥曲线中的几个命题及应用

江西师范大学数学与统计学院 (330022) 张思凡

作者现为2020级数学教育硕士研究生.

蝴蝶定理是平面几何中的经典命题，因其图形像一只偏偏起舞的蝴蝶而得名，该命题的证明及推广自其问世以来就一直吸引了众多数学爱好者的研究.实际上，蝴蝶定理在圆锥曲线中也有多种形式的变形和推广.本文撷取相关的几个命题，并对其在解题中的应用进行分析.

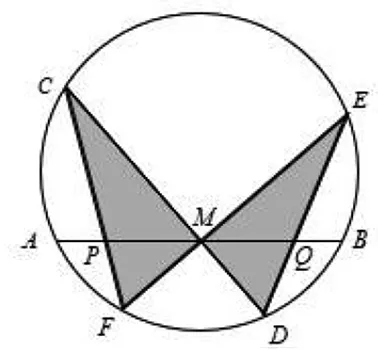
图1

蝴蝶定理如图1,过圆中AB弦的中点M作任意两弦CD和EF,连接ED和CF分别交AB于P、Q,则PM=MQ.

1.与蝴蝶定理相关的命题

命题1 如图2,AB是椭圆上平行于长轴的一条弦,M是AB的中点过M作椭圆的任意两条弦CD,EF,连CF,ED分别交AB于P,Q两点,则MP=MQ.

分析：这是椭圆上的蝴蝶定理,在命题过程中运用了蝴蝶定理的结构关系.要证明MP=MQ,可证明P,Q两点的横坐标之和为零.

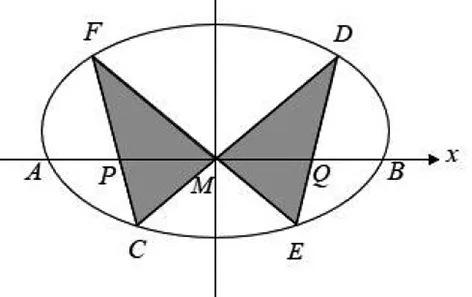
图2

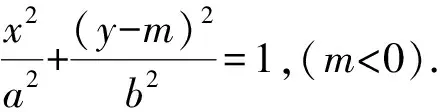
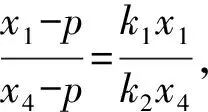
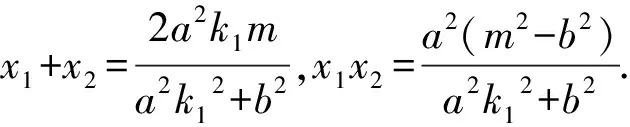
命题2 如图3,M是抛物线的弦PQ的中点，过M点引抛物线的任意两条弦AB与CD，连接AD,BC分别交直线PQ于E、F两点,则ME=MF.

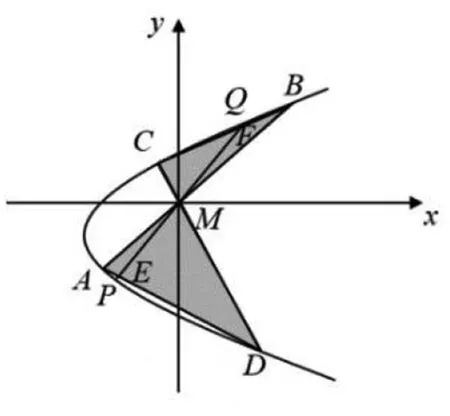
图3

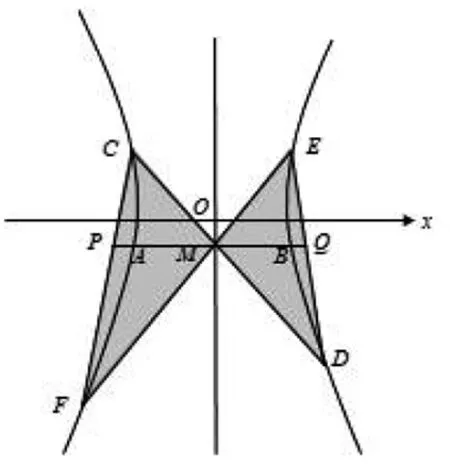
图4

命题3 如图4,AB是双曲线平行于x轴的一条弦，点M是AB的中点，过点M作双曲线的任意两条弦CD,EF，连CF,DE交AB于P,Q两点，则PM=MQ.

由此可将蝴蝶定理推广至一般的圆锥曲线，得到命题4，且命题2-4的证法与命题1相同.

命题4 在圆锥曲线中，过弦AB的中点M作任意两条弦CD,EF连CF,DE交AB于P,Q两点，则PM=MQ.

2.蝴蝶定理在解圆锥曲线题中的应用

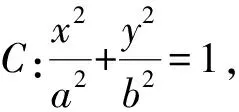
(1)求椭圆C的方程；

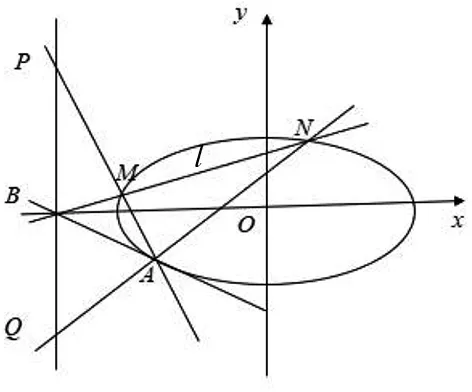
图5

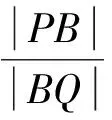
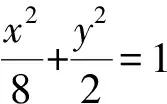
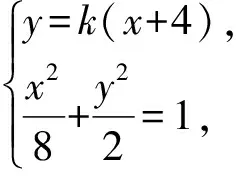
评析：此题将椭圆上蝴蝶定理中的点M引申到圆外，点B是椭圆外一点，虽然从题目条件中只看到了经过点B的一条弦，但经过计算可以发现直线BA是椭圆的一条切线，因此本题是椭圆上蝴蝶定理的一种特殊情况.本题解答的关键是求出P,Q两点的纵坐标，也结合了定理的证明方法，能较好的考查到学生逻辑推理、数学运算等数学核心素养.

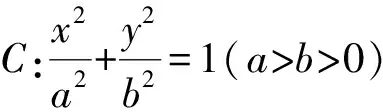
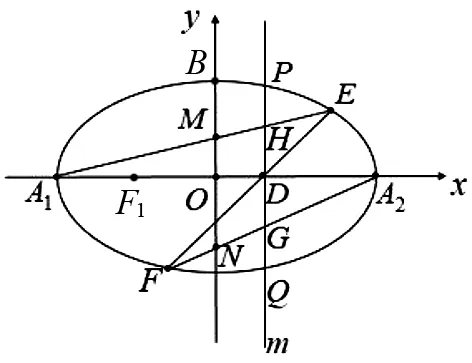
图6

(1)求椭圆C的方程；

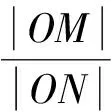
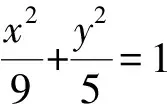
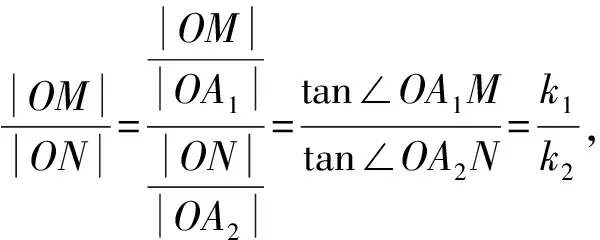
由椭圆上的蝴蝶定理可知,DG=DH.

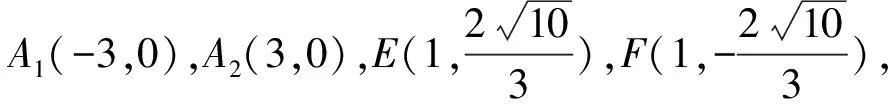
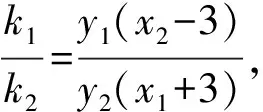
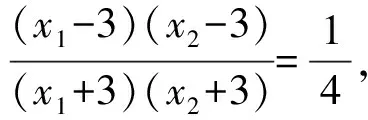
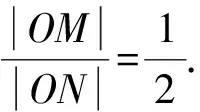
评析：本题的第(2)问是以蝴蝶定理为背景，且是以过椭圆长轴上一点的动直线引发的定值问题命制的题.解题的关键主要是运用转化的思想，即将线段的比值转化为直线斜率的比值，再通过结合椭圆上的蝴蝶定理，将问题求解.这能较好的考查到学生分析问题和解决问题的能力.