突破数学教学难点的两则教学案例

江苏省泗洪中学 (223900) 云广亮

教学难点是指学生在学习过程中不容易理解与接受的内容，或凭借学生个人能力难以解决的问题或任务.每个教学难点都是相对于学生的接受程度而言，维果斯基的“最近发展区”理论，明确揭示了教学难点形成的主要原因，是知识的难度超越了学生认知的最近发展区范围.为此，笔者对教学难点的突破，作了一定的实践研究.本文从两个教学实例谈谈如何在教学中突破教学难点，由此促进学生对知识的理解.

案例1“复合函数求导公式”的教学

问题求y=ln(2+x)的导数.

分析：在本节课之前，师生已经共同研究过如何用定义法求函数的导数问题、导数的基本运算法则以及初等函数的导数等内容.对照课程标准，并没有求“复合函数的导数的推导公式”的要求，对学生的要求仅仅是记忆并应用公式.

为此，笔者在首次教学本题时，就直接将复合函数的定义(y=f(g(x)))呈现给学生，并交代清楚其定义域、内函数、外函数，及内函数与外函数的值域、定义域间具有怎样的关系；而后提供一些常规的复合函数，要求学生进行内、外函数的辨认；接着提供复合函数的求导公式：如果y=f(g(x))，那么y′=f′(u)·u′(x)，且u=g(x)；最后带领学生进行相关的应用练习.

整个教学过程看似无可挑剔，一切都水到渠成.但笔者心里总觉得本节课少了点什么.为此，课后找来几个学生进行交流，学生一致认为本节课并不难，所有练习都没问题.就是对于为什么要求y′=f′(u)·u′(x)这一步，不太理解.

对于学生提出的问题，笔者进行了反思：本节课的教学难点是什么？结合学生所反映的情况与教学要求，发现复合函数的概念与求导公式为本节课的教学难点.对于概念这个难点，通过之前的教学已经化解，而求导公式却因忽略了求导过程的教学，学生就强行记忆，难怪整个课堂波澜不惊.

虽然课程标准并没有对复合函数的推导公式的形成过程作要求，但这并不能说明学生不需要理解推导公式的合理性.究竟该从什么角度出发，怎样突破这个教学难点呢？笔者将教学过程进行了如下改进：

师：我们一起来观察y=ln(2+x)的结构，大家思考一下，是否可用之前我们所学过的知识来求此函数的导数？

生1：好像不行，没有公式可以直接使用，定义也不好求.

师：当我们遇到困难时，该怎么办？

生2：化未知为已知.

师：对啦！现在我们来观察一下，这个函数与我们之前学过的哪种函数看起来类似？

生3：与对数函数(y=lnx)有点像，就是自变量的位置换成了代数式.

师：观察很到位，如此求导过程就变得复杂了，有没有什么办法能简化问题的难度？

生4：我们可以用换元法，让u=2+x，外函数就是y=lnu.

师：如此可求导吗？

师：难道和内函数的导数毫无关系吗？若求y=ln(x2+2)导数，该怎么办？

(学生分析并呈现结论，略)

师：由此可确定y=f(g(x))的导数吗？

生7：可以，据此可确定y′=f′(u)·u′(x)，u=g(x).

师：非常好！哪位学生愿意主动根据以探究过程，对复合函数的求导公式进行一个总结？

生8：复合函数的导数等于内函数的导数和外函数的导数的乘积.

评注：针对本题的教学改进，虽然教师没有带领学生推导复合函数的求导公式是如何得来的过程，但学生对该公式的合理性与内涵有了清晰的认识.有效地促进了学生对知识的理解，让学生充分认识到，公式并非是机械性的静态知识，还蕴含着丰富的内涵.

案例2“函数单调性”的概念教学

分析：这是高中阶段教学难点之一，学生认知障碍主要存在两个方面：第一，对区间(I)内的任意两个值如何理解；第二，怎样用数学语言来描述增函数与减函数.若学生对“任意”的理解不够透彻，就无法揭示函数单调性的本质，也无法体悟“用任意值x1、x2的大小关系对f(x1)、f(x2)的大小关系进行判断，能获得函数单调性的整体性质”.鉴于此，笔者作了以下教学设计：

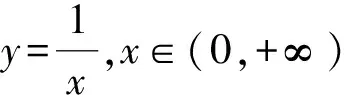
随着以上三个问题的逐个突破，教师初步提出单调性的定义，并将函数值y随着x的增大而增大或减小的函数统称为增、减函数.

问题2反比例函数与二次函数在其定义域上具有单调性吗？

针对此问，师生进行沟通，并获得进一步的完善定义为：若函数f(x)在区间I上满足自变量x增大，那么y会增大或减小，则称函数f(x)于区间I上为增或减函数，而区间I则为函数f(x)的增或减区间.

问题3已知函数y=x2,x∈R，当x的取值为-1，2，3，4，…，对应的y为1，4，9，16，…，我们可否认为函数值y随着x的增大而增大呢？是否能确定该函数为增函数呢？说明理由.

随着这个问题的解决，师生共同总结出这样一个结论：若想证明一个论断的成立，离不开科学、严谨的证明过程；而要确定一个论断并不成立，仅需一个小小的反例即可.

问题4一组函数的值，不会随着自变量的增大而增大，可确定该函数在区间I上并非是增函数.若想确定函数f(x)为增函数，需要多少组函数值y随自变量x的增大而增大呢？需要无数组吗？

评注：不少学生常用“代几组值”的方式，对函数的单调性进行研究，这种方法凸显出学生并未从真正意义上理解单调性的本质.反例的应用，则能让学生经历一个辩证的认知过程，从根本上理解什么是单调性，对概念的内涵与外延产生深刻理解.

同时，用数学语言表征增、减函数是本节课的教学难点.实践证明，教师可分以下几步逐层突破：

问题5对于“x增大、y增大、y减小”，该用怎样的数学语言来描述？

从数学的角度来看，大小一般可以理解为比较，那么一个x就不够用了.由此就引出了任意两数用x1、x2来表示，相对应的函数值则用y1、y2来表示.至于大小，从数学的角度出发，学生首先想到的就是“>、<”.

问题6x与y之间的对应关系，该如何用数学语言表达呢？

借助图象，在区间I上，当x1,x2∈I，从左往右看，图象呈上升趋势，如果x1y2.

问题7怎样避免出现以偏概全的现象？对于x1，x2有怎样的要求？请清晰书写出函数单调性的概念.

随着此问的探究，教师根据学生的所呈现的实际情况，适时给予点拨与引导，有效地深化了学生的函数单调性概念的理解.学生在概念书写过程中呈现出一些细节方面的错误，笔者一一进行纠正，以保证学生对概念理解的完整、规范，为完善认知结构夯实基础.

评注：教学设计时，为了突破学生语言表述的难点关，教师结合了图象、语言表述与数学符号表达相结合的方式，通过看、说、写等方式，将学生难以理解的概念先进行拆分，而后再重组，让学生从真正意义上实现对函数单调性的全面认识.

总之，教学难点具有不可小觑的教学价值，突破难点的过程，即为促进学生思维成长的过程.教师在处理教学难点时，应从化难为易的角度出发，在凸显学生主体性地位的同时，引导学生亲历难点的突破过程，让学生的收获多一些，课堂收益更广一些.