半群APk(n,n-1)的极大正则子半群

刘木村，罗永贵，高荣海

(贵州师范大学 数学科学学院，贵州 贵阳 550025)

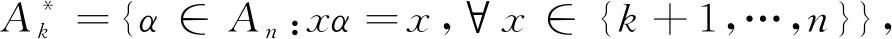
1 准备

设α∈APk(n,n-1),用im(α)表示α的象集,ker(α)表示dom(α)上如下等价关系:

ker(α)={(x,y)∈ dom(α)×dom(α):xα=yα}。对任意的t∈im(α),tα-1表示t的原象集。对0≤r≤n,文中用符号

表示半群APk(n,n-1)中元素的标准形式。

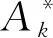
对任意α∈APk(n,n-1),记Dr={α∈APk(n,n-1):|im(α)|=r},0≤r≤n,则

为叙述方便,在半群APk(n,n-1)中引入如下二元关系[10-11]:∀α,β∈APk(n,n-1),有αLβ当且仅当im(α)=im(β),αRβ当且仅当ker(α)=ker(β),αJβ当且仅当|im(α)|=|im(β)|。令H=L∩R,D=L∨R,则L,R,H,D,J都是半群上的等价关系。易见L⊆J,R⊆J,D=J。

设S是半群,对任意的a∈S，分别用La,Ra,Ha,Da,Ja表示a所在L-类,R-类,H-类,D-类,J-类。

Dn-1的幂等元有如下形式:

设n≥3,3≤k≤n,记

文中未定义的符号及术语参照文献[10-11]。

2 主要结果及证明

为叙述方便,考虑奇异部分变换半群SPn的顶端Dn-1={α∈SPn:|im(α)|=n-1},对任意p,q,s∈Xn,定义

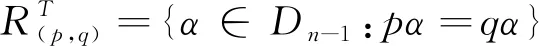
引理1设1≤r≤n-1,则APk(n,r)是正则半群。

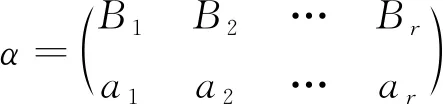
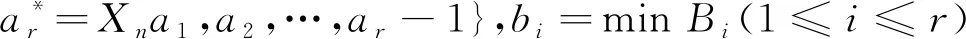
引理2[10]设S是半群,对任意的a∈S,则Ha至多含有一个幂等元,若Ha含有幂等元,则Ha是群。

引理3[11]设D是半群S的正则D-类,a,b∈D,则H-类Hb包含a的逆元当且仅当H-类Ra∩Lb和Rb∩La包含幂等元。

引理4 设n≥3,α∈Dn-1,则1≤|E(Rα)|≤2,|E(Lα)|=n。

引理5设G是交错群A*k的极大子群,则S1=G∪SPn为半群APk(n,n-1)的极大正则子半群。

证明第一步:证明S1是子半群。对任意的α,β∈S1,若α,β∈G,则αβ∈G;若α,β∈SPn,则αβ∈SPn⊂S1;若α∈G,β∈SPn,由|im(αβ)|≤min{|im(α)|,|im(β)|}可知,αβ∈SPn⊂S1。因此,S1是半群APk(n,n-1)的子半群。

第二步:证明S1是正则的。由于G是群A*k的极大子群,则对任意的α∈G,存在α的逆元α-1∈G,使得αα-1α=α,从而G是正则的,即S1是正则的。

第三步:证明S1是极大正则子半群。设S是半群APk(n,n-1)的极大正则子半群且S1⊂S,任取α∈SS1,则α∈A*kG。由于G是群A*k的极大子群,于是〈G∪{α}〉=A*k,从而〈G∪{α}∪SPn〉=〈A*k∪SPn〉=APk(n,n-1)。因此,S1是半群APk(n,n-1)的极大正则子半群。

引理6设1≤i,j≤k且i≠j,则S2=A*k∪Dn-2∪Dn-1(∪i,j∈[1,k]i≠jRT(i,j))是半群APk(n,n-1)的极大正则子半群。

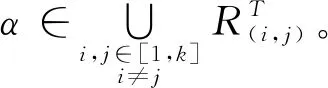
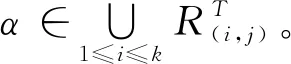
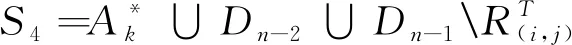
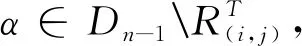
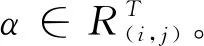
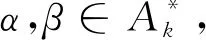
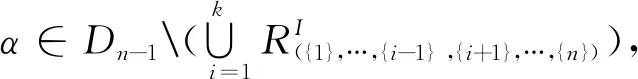
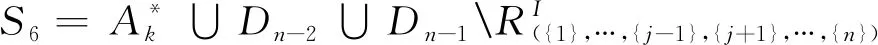
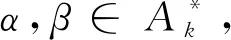
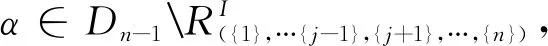
3 主要结论

定理1半群APk(n,n-1)的极大正则子半群有且仅有如下6类:

(1)S1=G∪SPn;

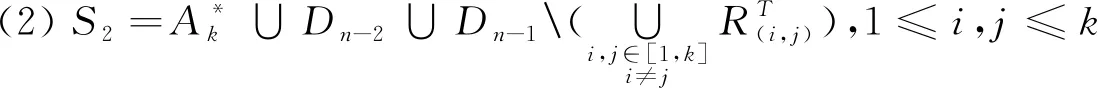
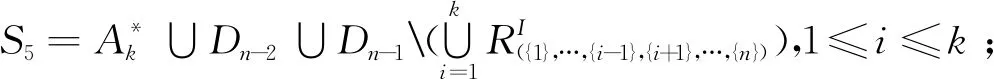
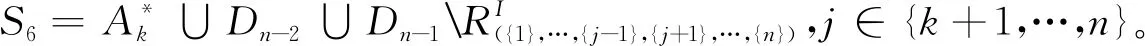
证明由引理5至引理10可知，S1,S2,S3,S4,S5和S6是半群APk(n,n-1)的极大正则子半群。

用反证法证明APk(n,n-1)的极大正则子半群只有定理中的形式。假设S是半群APk(n,n-1)的极大正则子半群,且不是定理中的形式。以下分两种情形讨论:

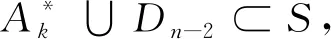
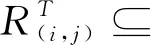
综上可知,半群APk(n,n-1)的极大正则子半群只有定理中的形式。