电离能下降对于硅等离子体辐射不透明度影响的研究

胡 峰， 孙 言 ， 梅茂飞， 韩 崇， 潘跃武， 吴 苗， 刘 浩

(1.徐州工程学院 物理与新能源学院， 徐州 221018； 2.徐州工程学院 机电工程学院， 徐州 221018；3.安徽新华学院 通识教育部， 合肥 230088； 4.中国工程物理研究院 激光聚变研究中心， 绵阳 621900)

1 引 言

辐射不透明度对于天体物理和激光惯性约束聚变中等离子体的输运有着至关重要的作用. 在天体中，核聚变的能量通过光辐射、电子辐射以及转化从内部向外输运，其中光辐射占主要地位. 不透明度决定辐射输运的效率，影响天体的特性[1]. 很多元素例如，铁、硅、氧、碳、镁、铝等对星体的不透明度有着明显的贡献[2]. 本工作讨论的硅等离子体，国内外开展了大量的实验和理论研究[3-5].

但是在等离子体中，存在着大量的带正电的离子、带负电的离子以及中性的原子，它们之间相互联系、相互影响，这种影响即等离子体的屏蔽效应. 由于此效应的存在，束缚电子不像在孤立原子中，只受到核与其他束缚电子的作用，还要受到来自附近自由电子和其他离子的影响，这就导致了离子的能级结构发生变化，出现电离能下降的现象(Ionization potential depression，IPD). IPD与等离子体的成分、电离分布、热力学、输运性质息息相关，IPD的准确测量对于整个实验的模型检验和方案设计都至关重要[6].

熊刚等人在神光II装置上通过测量硅薄膜研究了温度在72±5 eV，密度为 6.0±1.2 mg/cm-3的硅等离子体的辐射不透明度[3]，随后Jarrah等人用细致能级法和超级组态优化(SCO)方法对该实验进行了解释，但是结果与实验结果相差较大[5]. Iglesias指出很多理论模型都没有考虑粒子数的涨落，而这对于IPD的精确求解显得尤为重要[7]. 因此本文在前期工作的基础上[8, 9]，结合熊刚等人的实验，探讨基于涨落模型的IPD对于硅等离子体辐射不透明度的影响.

2 理论计算方法

辐射不透明度的计算方法在文献[8, 9]中已有详细描述，其中原子结构能级、跃迁等基础信息由文献[10]使用的方法给出，这里仅对IPD做简要的介绍.

描述IPD主要有两种经典的模型，一种是Ecker和Kröll的EK模型[11]，另一种是Stewart和Pyatt的SP模型[12]. 本文主要考虑涨落对于SP模型的修正.

(1)

温度较高时，SP模型(1)简化成公式(2),

(2)

考虑涨落之后，公式(2)变成公式(3)，其中Ne是自由电子数目.

(3)

需要强调的是，此时的Ne不是平均值而是邻近离子的自由电子数目. 假设这些离子在晶格里面都是近似不动的，则自由电子的密度引起了IPD的涨落. 可以由泊松公式给出理想玻尔兹曼分布气体的粒子数涨落，见公式(4).

(4)

这样公式(3)就和公式(4)，构成了含涨落的IPD公式.

需要说明的是，在理想的简并电子气中，粒子数涨落可以由公式(5)给出：

(5)

其中，T是温度，μ是化学势. 将公式(4)带入公式(5)，则有公式(6)

(6)

其中公式(6)中有

(7)

(8)

上述公式的α=μ/T，Γ(x)为伽玛函数. 经过变换可以得到粒子涨落的高斯分布函数为：

(9)

3 结果与讨论

熊刚等人的实验给出了硅等离子体的温度与密度范围[3]，图1比较了温度为72 eV，密度为6 mg/cm-3时的离子布居，其中NLTE是Jarrah等人基于非局域热动平衡( Nonlocal thermodynamic equilibrium )给出的结果. 图1可以看出本文和Jarrah等人两种方法结果较为一致，当前等离子体主要离子成分为Si7+～Si13+，其中 Si8+～Si12+占主要部分. 熊刚等人给出的平均电离度为10.07，NLTE为9.88，SCO为10.78，当前为9.97，可以看出考虑了IPD之后，与实验结果更加接近. 同时从图1可以看出，当前计算值的离子丰度更为集中，当前计算的Si9+，Si10+，Si11+占比分别为26.7%，41.7%和22.7%，与实验值给出的Si9+，Si10+，Si11+占比26.2%，42.0%和22.7%基本一致.

图1 硅等离子体的电离分布

为了更好地探讨IPD的影响，图2比较了温度为72 eV，温度为72 eV，密度为6 mg/cm-3时的离子布居，考虑SP修正、SP与EK三种模型的离化度分布，从图中可以看出，离化度为10时，EK离化度高于SP修正、SP，数值高0.001，离化度为9时，SP修正较高，高出SP与EK不到0.001. 总体来说，三种模型离化度分布较为一致，这是因为当前实验产生的密度较低.

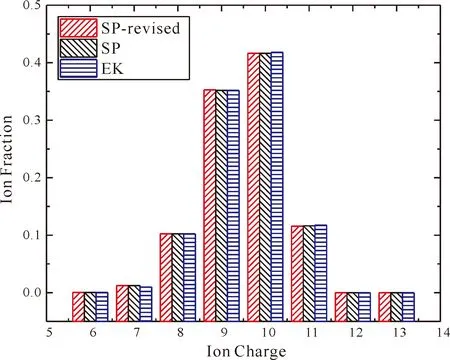
图2 72 eV不同模型的离化度分布

图3比较了温度为72 eV，不同电子密度的辐射不透明度. 可以看出当离化度低时，离化度随密度的增加而增加，离化度高时，离化度随密度的增加而降低. 图中两个明显峰在1817 eV和1840 eV附近，分别对应的是1s22p-1s2p2和1s22p23p-1s2p33p跃迁[3]. 需要说明的是如果考虑细致谱项，1s22p-1s2p2跃迁对应的能量为1840.07 eV、1841.71 eV和1842.71 eV，从侧面证明了实验谱线辨识的复杂性. 图4比较了密度为0.006 mg/cm-3，不同密度的辐射不透明度. 可以看出，电子温度较高时，波峰面积明显高于低温情况. 1817 eV与1840 eV的峰峰比值从0.0048 g/cm3时的0.662变为0.0072 g/cm3时的0.241，能量更为集中.

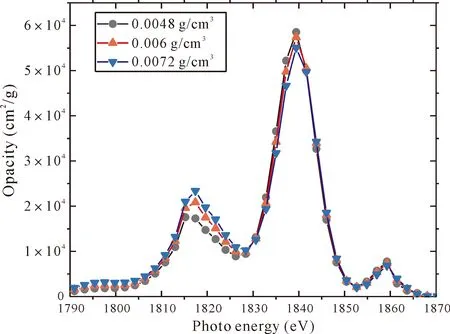
图3 温度为72 eV硅等离子体的辐射不透明度

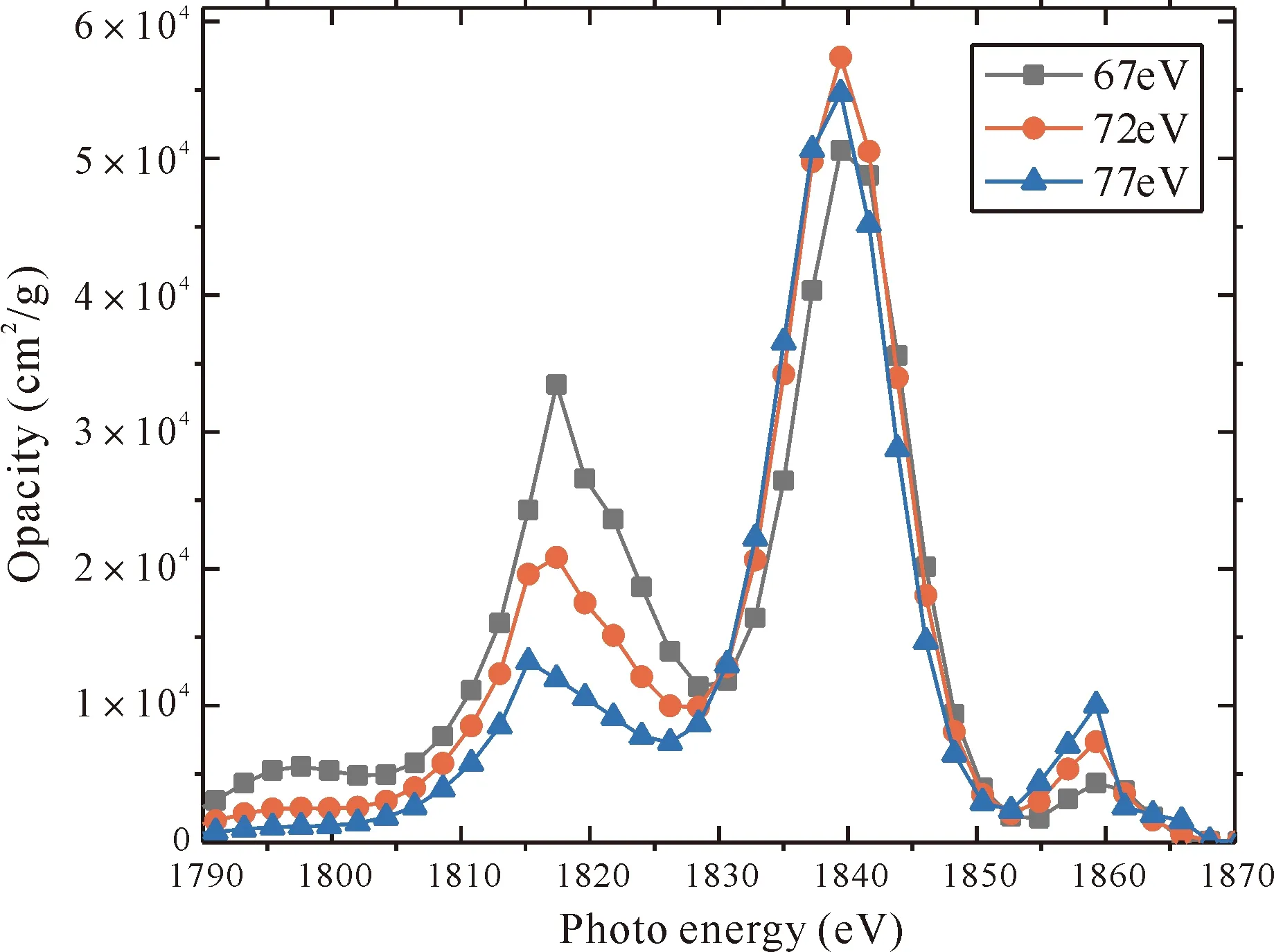
图4 密度为0.006 mg/cm-3硅等离子体的辐射不透明度

我们在表1对比了，温度在67-77 eV，密度在0.0048 -0.0072 g/cm3时范围内的化学势和平均离化度，因为熊刚等人实验给出的密度较低，因此平均离化度都比较高，且较为接近，这也是实验不能给出精确温度和密度的一个重要原因之一.

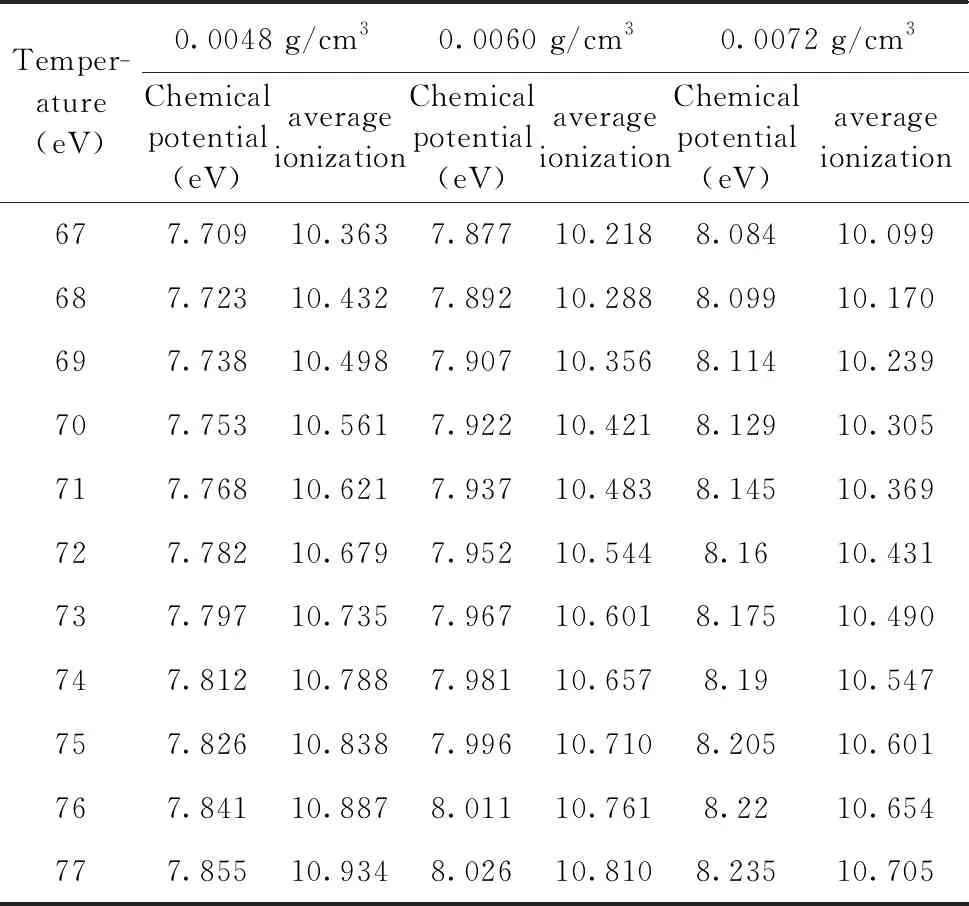
表1 硅等离子体的化学势(eV)和平均离化度

Hill 和Rose对惯性约束聚变实验中用的靶丸

进行了详细的分析，指出了硅丸形成的等离子体的密度在10-3～10 g/cm-3，温度在10～360 eV范围内，才能满足点火的要求[13]. 这里需要指出的是，此处的硅等离子体是含有碳等掺杂物的. 随后，Benita对此范围的等离子体进行了分析[14]. 因此，我们在图5中给出了10-5-10 g/cm3的硅等离子体平均离化度，当密度为10-5g/cm3时，离化度为11.999. 在10-5到10-3g/cm3的硅等离子体平均离化度均为11.90附近，当密度增加到1g/cm-3时，平均离化度只有8.656，与Bentia给出的8.772有大概0.1的差异，这是因为本文给出的是不掺杂的平均离化度[14].

图5 温度为100 eV，不同密度的硅等离子体的平均离化度

依据Hill 和Rose等人给出的密度范围，我们给出了0.1 ～10 g/cm3,能量在0～3000 eV范围内硅等离子体的辐射不透明度. 从图6中看出，在0.1 ～10 g/cm3密度范围内，不透明度的整体趋势比较一致. 图中三处明显的峰，其中能量1815～1840 eV，三种密度形成的吸收峰都较为明显，这与熊刚等人的实验结果相一致. 但是当密度升高到10 g/cm3，在2039～2353 eV附近，对应的类He峰消失了，说明了密度升高导致离化率下降，这与Bentia给出的掺杂情况相一致[14].

图6 温度为100 eV硅等离子体的辐射不透明度

4 结 语

本文在经典的电离能下降模型的基础上，考虑涨落效应带来的修正，详细计算了不同温度、密度条件下的离化度、辐射不透明度以及化学势等物理量，所得的结果与熊刚等人实验结果符合较好，且优于W.Jarrah等人用细致能级法和超级组态优化得出的结果，对分析已有的实验结果和指导未来的实验也有重要的意义. 然而需要指出的是，当前计算的等离子体是非混合物，下一步需要考虑混合物对IPD的影响.