考虑碳排放的多式联运多目标路径规划

邓红星,宋雅婧

(东北林业大学 交通学院， 哈尔滨 150006)

0 引言

随着我国碳达峰、碳中和战略目标的提出，交通运输作为碳排放的重点领域之一，在全面绿色低碳转型、优化交通运输用能结构和提高交通运输组织效率方面愈发受到关注。目前，多式联运正在成为国家间运输业务活动的主要组织形式和未来物流的主要发展趋势，也是我国物流行业发展的主要研究方向。作为重要的运输方式之一，多式联运在提高运输效率的同时能够有效降低运输成本和运输时间，因此考虑联运过程碳排放，结合运输费用和运输成本目标，正确选择多式联运运输方式以及运输路径，对低碳交通的发展具有现实意义。

对于多式联运路径规划问题，国内外学者已经进行了众多研究。具体可以分为2个方面：一是考虑运输成本与时间方面，Gocmen等[1]将运输成本最优作为主要目标，提出了一种基于混合整数规划的集装箱运输方式分配的数学模型；Corman等[2]考虑多式联运网络中的成本和时间，以用户的广义成本最小化为平衡点提出了一种分配模型；户佐安等[3]构建由多个决策主体目标构成的广义费用函数，建立以广义费用最优为目标的多式联运路径优化模型；李魁梅等[4]结合运输工具成本，建立以综合运输成本最低为目标的多式联运路径优化模型，设计混合蝙蝠算法对模型进行求解；刘松[5]将转运耗时转化为路段权值，建立了以运输时间和转运时间最少为目标的多式联运路径优化模型；李兆进等[6]以总运输成本为目标函数，构建混合整数规划模型，开发了一种列生成启发式算法；耿娜娜等[7]以成本最低、时间最短为目标建立优化模型，用中欧班列运输实例对模型进行求解。二是考虑低碳环保因素对多式联运路径进行设计与优化，Wang等[8]将碳排放作为一个独立的评估指数，进行多式联运参数动态计算；Yi等[9]建立了包含运输成本和和温室气体排放成本的双目标优化模型，通过实例对模型进行验算；Demir等[10]将环境因素纳入运输规划，在此基础上设计了模型和算法，基于欧洲腹地多式联运案例进行研究分析；柳培学等[11]建立了以运输费用和碳排放指标最优的多式联运路径优化模型，设计算例进行求解；陈维亚等[12]构建碳税成本和质量成本构成的多式联运路径优化模型，设计遗传算法进行求解；张旭等[13]对不确定需求与碳交易价格下的多式联运路径优化问题进行研究，设计基于蒙特卡罗采样的灾变自适应遗传算法；成耀荣等[14]从多式联运经营人的角度，建立考虑碳排放的多任务多式联运路径综合优化模型。

上述学者主要以运输成本、运输费用或碳排放最小进行多式联运单目标问题研究，部分学者建立了考虑碳排放或运输费用的双目标规划模型，极少有研究者考虑多目标规划的多式联运路径问题。运用单目标求解虽然可以得到最优解，但无法得到多目标的最优解集，更不能根据不同的运输要求灵活变通运输方案。同时，单目标规划忽略了现实情况下决策目标的多样性[15]。因此，本文将对碳排放量、运输费用和运输时间综合考量，构建多式联运多目标最优路径及方式选择模型，运用算例说明在不同应用场景下如何选择最优运输方案。

1 问题描述与建模

1.1 问题描述及假设

对货物运输的多式联运路径和方式选择进行研究，具体如下：某批货物q从起点运送到目的点，中途经过若干个路网节点，任意相邻2个节点之间有铁路、公路和水路一种或多种运输方式，不同运输方式运输时和在中转节点转换运输方式时产生的运输费用、运输速度和碳排放系数都不同。在上述条件下，寻求最优的联运路径。

本文构建的多式联运路径多目标规划模型基于以下假设：

1) 一批货物不能进行拆分运输；

2) 某种运输方式的速度由其平均速度表示；

3) 相邻路网节点之间只能采用一种运输方式；

4) 路网节点处只能产生一次运输方式的改变；

5) 运输时间由路段长度及某种特定运输方式的速度决定。

1.2 模型建立

具体参数和变量的说明如下：

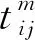
本文以运输碳排放、运输成本、运输时间三者最小作为目标函数建立模型，并根据问题假设设置约束条件，具体表示为：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

式(1)为目标函数1，表示运输过程中的碳排放量，第一部分是货物在路网节点之间运输产生的碳排放量，第二部分是货物在路网节点进行中转时转换运输方式产生的碳排放量；式(2)为目标函数2，表示运输过程的费用成本，第一部分是货物在路网节点之间运输产生的费用成本，第二部分是货物在路网节点进行中转时转换运输方式产生的费用成本；式(3)为目标函数3，表示运输过程所花费的时间，第一部分是货物在路网节点之间运输所花费的时间，第二部分是货物在路网节点进行中转时转换运输方式所花费的时间；式(4)表示运输时间由运输距离和运输速度决定；式(5)表示相邻两路网节点间只能采用一种运输方式；式(6)表示在某个路网节点最多只能进行一次运输方式的转换；式(7)保证运输网络的连贯性。

2 算法设计

NSGA-Ⅱ算法是带有精英策略的非支配排序遗传算法，具有收敛性能好和运行速度快的优点，具体步骤如下：

步骤1染色体编码。染色体中每3位二进制编码表示1个节点，铁路、公路和水路运输方式分别用100、010、001表示。如图1所示编码，表示为1条经过5个路网节点A、B、C、D、E的多式联运路径，从路网节点A开始运输，节点A和B之间采用公路运输，不经过节点C，节点B与D之间采用水路运输，节点D与E之间采用铁路运输。

图1 编码示意图

步骤2生成初始种群。随机生成规模为N的初始种群，对其进行非支配排序，采用非支配遗传算法对其进行操作得到第一代种群个体。

步骤3选择算子。从第二代种群之后，合并父代和子代种群，使用快速非支配排序对新种群进行分层，并计算相同层内个体拥挤度，其中子代采用锦标赛算子产生。

步骤4交叉变异。对新一代种群进行单点交叉变异。如图2所示，染色体1和2在a点进行交叉，在b处进行变异。

步骤5精英策略。按照优先度进行非支配排序，以层级从低到高的顺序将个体选入下一代父代种群，当添加到某一层级个数超过正常种群规模，则比较此层级个体拥挤度，优先选择拥挤度大的个体，余下部分淘汰，如此反复，直到达到最大迭代次数。算法流程如图3所示。

3 算例设计与分析

3.1 算例设计

黑龙江省一直是我国对俄罗斯贸易的重要据点。本文将黑龙江省会哈尔滨设为货运起始点，将中俄经济走廊的重要枢纽城市抚远作为黑龙江对俄出口边境口岸，将抚远对应的哈巴罗夫斯克口岸作为货运终点。

考虑文献[16]中提到的黑俄国际货运通道上的节点和边境口岸分布、黑龙江省交通运输厅提出的“145”三级枢纽城市和“521”三类运输通道，选取这些路线上的重要节点城市作为路线节点，具体选取城市节点及编号如表1所示，结合实际运输线路进行抽象，得到运输网络示意图如图4所示。

表1 具体选取城市节点及编号

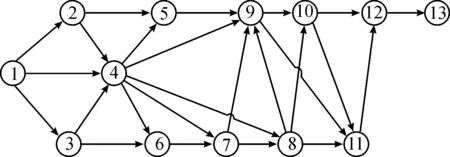
图4 货物出口简易运输网络示意图

黑龙江省对俄出口货运通道的航空运输通道存在一定局限性，此处路网节点之间的运输方式只考虑铁路、公路和水路运输。具体城市节点间存在的运输方式及相应运输距离如表2所示。

表2 节点城市间相应运输方式及距离 km

假设某企业有一批重3 t的粮食货物要从哈尔滨运往俄罗斯哈巴罗夫斯克，有11个中间路网节点，具体城市节点及编号见表1，简易运输网络见图4，具体节点之间可采用运输方式和运输距离见表2。表3为采用各运输方式时的碳排放系数、运输速度和运输费用，表4为各运输方式进行转换时产生的碳排放系数、转运时间和转运费用。采用设计的NSGA-Ⅱ多目标优化遗传算法对算例进行求解，设定种群规模为100，交叉概率为0.9，染色体长度为13*3，变异概率为染色体的倒数，种群遗传代数为300。

表3 各运输方式指标参数值

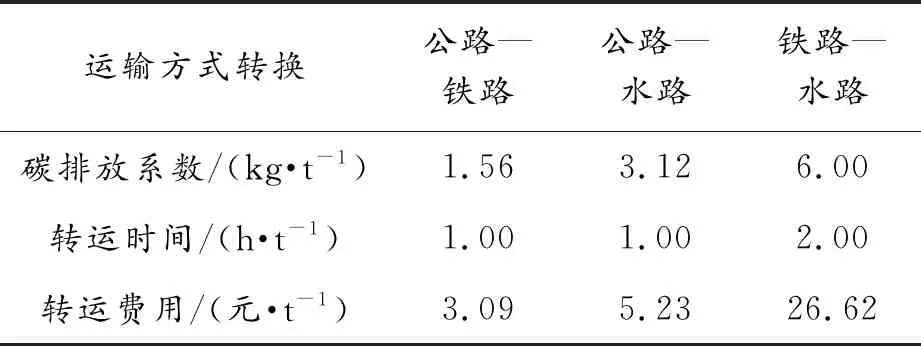
表4 转化运输方式时的指标参数值

3.2 结果分析

采用设计的NSGA-Ⅱ多目标优化遗传算法，运用Matlab编程实现算法，运行平台为Intel(R) Core(TM) i7-7700HQ CPU @ 2.80GHz，8 GB内存的计算机。运行程序后得到多个帕累托非支配解，有效解集分布见图5。图中每个点对应一个非支配解，包括运输路线和联运方式，以及此多式联运路径产生的碳排放量、运输费用成本和运输时间。

图5 帕累托有效解集分布

实际帕累托有效解集中的每个解都有各自的优势，在对俄出口多式联运路径选择时，可以根据具体的需求选择对应的帕累托解。此处从解集中选取有代表性的部分解，具体见表5。

表5 帕累托代表解

解集中前3个运输方案为对应的目标函数值最小的方案，方案4为随机挑选的折中方案。如对碳排放有较高要求，应选择方案1，此方案碳排放是方案2的20.74%，是方案3的5.76%；如对运输费用有较高要求，应选择方案2，此方案运输费用是方案1的67.9%，是方案3的56.34%；如对运输时间有较高要求，应选择方案3，此方案运输时间是方案1的22.26%，是方案2的23.21%；折中方案4的碳排放和运输费用小于方案3，运输时间小于方案1和方案2。

在实际运输过程中，多式联运参与者会对3种目标函数有不同偏好程度，此时可以利用秩和比综合评价方法对3个指标赋予一定权值，得到不同运输要求下的最优解。此处讨论3种情况：① 不对3个目标量设权重，即权重相同，可得到最优解1；② 假设碳排放、运输费用和运输时间权重为[0.2,0.45,0.35]，可得到最优解2；③ 假设碳排放、运输费用和运输时间权重为[0.5,0.3,0.2]，可得到最优解3。3种情况下最优解集见表6。

表6 3种情况下最优解集

由表5和表6可以看出，公路运输的运输时间明显要小于铁路运输和水路运输，但由于公路运输费用高，不适合作为单一运输方式进行长途运输，可以作为衔接或者联运中的短途距离运输，且公路运输碳排放较高，对环境污染较大；有水路运输和铁路运输参与的联运方案运输费用及碳排放量都处于较低值，但相应会增加运输过程的时间；铁水、公水、铁公等多式联运能够发挥各种运输方式的优势，从而降低碳排放量、运输成本，并节约运输费用。

4 结论

以多式联运过程中的碳排放量为出发点，结合运输过程中产生的费用和时间，同时考虑在运输中转节点转换运输方式时的影响，构建了以碳排放、运输费用成本和运输时间最小为目标的多式联运最优路径选择规划模型。采用NSGA-Ⅱ算法对算例进行求解，运用秩和比法对帕累托有效解集的解进行评估，说明在不同应用场景时如何达到最优，验证了模型和算法的可行性和实用性，可为决策者选择合理货物联运路径提供参考。