共轴式刚性双旋翼悬停气动载荷CFD仿真分析
石力王,胡明辉,2,陈广艳,陈伦国,石万凯,2,曾 利
(1.重庆大学 机械与运载工程学院,重庆 400044;2.重庆大学 机械传动国家重点实验室, 重庆 400044;3.中国航发湖南动力机械研究所,湖南 株洲 412000;4.直升机传动技术国防科技重点实验室,湖南 株洲 412000)
0 引言
相比于常规直升机旋翼,共轴式刚性双旋翼可以显著提高直升机运行时的工作拉力,无需安装力矩平衡尾桨,具有结构紧凑、气动效率高等特点,在高速直升机上应用广泛。但共轴式双旋翼相较于单旋翼,气动特性更为复杂,上下两副旋翼的旋向相反,旋翼周围流场为非定常流场[1],上下两副旋翼的间距小,上下旋翼间产生严重气动干扰。气动干扰不仅影响直升机的飞行平衡及其操纵稳定,也使得共轴式双旋翼气动载荷计算难度骤增[2]。在正向设计直升机旋翼的时候,动力传动系统的匹配是关键步骤之一,旋翼的拉力和力矩是选择直升机发动机和减速器的重要指标之一。因此,建立精准的共轴式双旋翼气动载荷分析模型,分析旋翼设计参数对其气动载荷的影响,探究平衡上下旋翼力矩方法,对于指导共轴式刚性双旋翼直升机的正向设计具有重要意义。
国内外众多研究人员致力于开发精确有效的共轴式双旋翼气动载荷数值计算方法。自由尾迹、动量理论以及叶素理论等理论方法是开展共轴式双旋翼气动建模的常用方法[3-6]。此外,部分学者将自由尾迹法与升力面法以及二阶升力线法相结合,进行双旋翼悬停工况下的建模分析[7-8]。上述方法多属于势流法,虽计算量小,却无法准确捕捉激波失速、桨尖涡流与气流分离等现象,因此计算精度较低。为准确描述流体域内非定常现象,考虑涡量运输与气体粘性对流场的影响,提高共轴式双旋翼气动载荷计算精度,基于嵌套网格与Euler/Navier-Stokes方程的CFD方法得到研究人员的青睐。Lakshminarayan[9-10]建立了一套运用滑移与嵌套网格的混合网格方法,研究了共轴式双旋翼气动特性变化规律,但滑移网格会导致部分通量的损失。叶靓等[1]基于非结构嵌套网格与网格自适应技术,提出了一套共轴式双旋翼气动特性数值求解器。朱正等[11]则运用基于运动嵌套网格的CFD方法,对双旋翼非定常流动干扰进行机理分析。
上述工作为共轴式双旋翼的研究提供了重要参考,却缺乏上下旋翼力矩平衡方法的研究,由于上下旋翼气动干扰严重,在无平衡尾桨的情况下,上下旋翼间的力矩差严重影响共轴式刚性双旋翼直升机的飞行平衡与操纵稳定。鉴于此,本文基于先进的计算流体力学,建立了适用于共轴式刚性双旋翼气动性能求解的方法,利用雷诺时均Navier-Stokes(RANS)方程、双时间方法和非结构运动嵌套网格等技术,针对共轴式刚性双旋翼悬停状态进行了气动载荷仿真分析,并通过改变上旋翼的总距角,研究双旋翼总距差对上下旋翼气动载荷的影响规律,获得了双旋翼的最佳总距角,在保证拉力达标的情况下,实现上下旋翼的力矩平衡,从而可以指导后期的关于直升机发动机的选型和动力传动系统的正向设计。
1 运动嵌套网格与数值方法
1.1 运动嵌套网格生成
在众多网格生成技术中,1983年Steger等开创的嵌套网格技术,利用多块子域网格对计算域进行全局覆盖,在不同网格重叠部分采用信息共享的方法来实现信息交换,并不强制要求网格之间进行无缝拼接,极大减轻了子域网格生成的难度,而且能够保证生成的子域的网格品质,因此嵌套网格技术在实际工程的复杂外形的数值模拟和研究实验当中得到了广泛的应用。
本文将计算悬停状态下上下旋翼不同总距下共轴式刚性双旋翼直升机的气动载荷。上下旋翼由2片NACA 0012翼型桨叶构成,旋翼半径为8.53 m,弦长0.41 m,桨叶无扭转和尖削,NACA 0012翼型截面形状如图1所示,双旋翼算例模型的具体参数如表1所示。

图1 NACA 0012翼型截面示意图
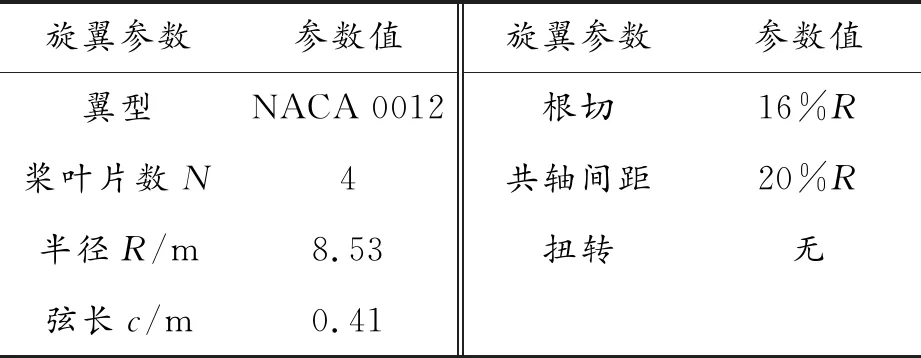
表1 NACA 0012翼型参数
本文生成的运动嵌套网格系统由两个层次的网格组成:一是围绕旋翼表面生成的近似正交的贴体非结构网格,其与旋翼固定连接并随其同步周期性旋转运动,用于近场尾涡的捕捉和模拟旋翼表面附近的流动;二是将旋翼表面贴体网格包围的背景网格,它是静止不动的,属于笛卡尔网格,模拟旋翼远场流动特征及流场结构。为了能够准确地捕捉桨尖涡,对背景网格进行3层加密处理,并将背景网格扩展至较大的计算域以减小远场边界的影响。非结构运动嵌套网格系统划分结果如图2所示。

图2 双旋翼的非结构运动嵌套网格系统
1.2 控制方程与数值求解方法
为了高效模拟非定常共轴式刚性双旋翼气动载荷[12],本文利用有限体积法,基于STAR-CCM+商业软件求解非定常不可压Reynolds时均Navier-Stokes方程(URANS)。湍流模型采用一方程Spalart-Allmaras模型,S-A模型为航空旋转机械领域广泛运用来计算URANS粘性系数的,比零方程模型计算量更大但结果更加精确,比两方程模型计算量更小但稳定性更好,不需要网格处理得特别精细,更适合于非结构网格[13]。
固定坐标系下的N-S方程如下:
(1)
式中:W为流场守恒变量,可以表示为W=[ρρuρvρwρE]T;F(W)为无黏通量;G(W)为黏性通量,分别表示为:
(2)
(3)

(4)
式中:T为流体温度;k为热传导系数。本文采用有限体积法求解上述主控方程,时间离散上采用双时间法,伪时间步长为多步迭代格式,湍流模型为Spalart-Allmaras模型;边界条件中旋翼表面定义为无滑移壁面边界条件,背景边界则为压力出口。
悬停状态下上下旋翼转速相等为300 r/min,转向相反,定义上下旋翼贴体网格区域为旋转体,转速和方向与旋翼保持一致。在STAR-CCM+对求解模型进行选择设置完成后,即可开始计算求解,具体设置如表2所示。
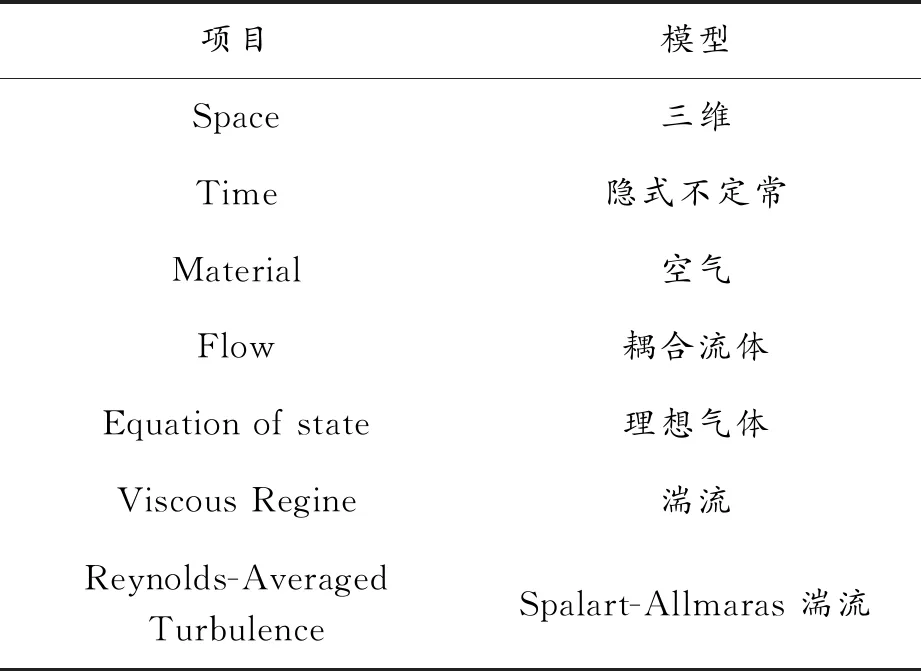
表2 求解模型设置
2 算例及结果分析
共轴式刚性双旋翼直升机具有上下布置的两副旋翼,两副旋翼转速相等转向相反,可以抵消反力矩,充分释放前行桨叶的升力潜能,大幅提高直升机的飞行速度。但是共轴式双旋翼流场中存在较单旋翼流场更严重的桨-涡干扰和涡-涡干扰等气动干扰现象,上旋翼产生的下洗流改变了下旋翼迎风角,在上下旋翼总距相同的条件下,上下旋翼气动特性存在差异,导致上下旋翼间力矩不平衡,影响直升机飞行稳定性。因此,探寻上下旋翼力矩平衡方法是开展共轴式刚性双旋翼直升机正向设计的必要过程。
调整上下旋翼的总距角是减小上下旋翼力矩差的关键手段,共轴式刚性双旋翼系统的本质是利用转向相反的上下旋翼来平衡反力矩,但是因为上下旋翼间气动干扰的存在,上下旋翼受到的气动力不同,使得反力矩无法平衡,这时只能通过上下旋翼的总距差动来平衡上下旋翼间由于气动干扰带来的力矩差。
下面算例中以不同的上下旋翼总距角来分析共轴式双旋翼的气动载荷,探究总距角和共轴式刚性双旋翼上下力矩与拉力的关系,来获得符合要求的总距差,各个算例旋翼的总距角情况如表3所示。

表3 算例情况
在对所有算例进行仿真分析前,本文基于算例1工况,共计开展了6套不同网格数量级的数值计算,单片桨叶网格数量范围为60 712~110 856,且每套的加密区范围和尺寸相同。发现单片桨叶网格量增加到92 057后,拉力系数已经收敛,不再受到网格数量的影响。具体的上旋翼拉力系数随网格数量的变化情况如图3所示。因此,在确保网格无关的前提下提升数值仿真效率,同时考虑工作站的计算能力和计算时间的问题,所以最终选择了单片桨叶为10万左右的网格数量进行计算。

图3 网格无关性验证
下面依次对每个算例进行数值仿真计算,待迭代计算收敛,得到稳定旋翼拉力和力矩周期解,取旋翼旋转一周的数据进行比较分析。
图4—图6为不同总距差下,共轴式刚性双旋翼在悬停状态下上旋翼和下旋翼的拉力变化曲线对比图。

图4 上旋翼拉力变化曲线

图5 下旋翼拉力变化曲线

图6 上下旋翼拉力和变化曲线
由图可见,在上下旋翼桨叶形状大小完全相同的情况下,随着上下旋翼总距差的改变,上下旋翼拉力的变化趋势一致,呈周期性变化,其主波动周期大约为90°,拉力幅值和波动幅度有所改变,呈“载荷效应”“厚度效应”与“涡诱导效应”[14]。
保持下旋翼总距角不变而增大上旋翼总距角,总距差增大,而翼型剖面存在一定的厚度和迎角,因此上旋翼下表面与下旋翼上表面间距随上旋翼总距角的增大而缩小,双旋翼间的气体流速增大,从而使上旋翼的下表面与下旋翼的上表面压强减小,导致上旋翼拉力减小、下旋翼拉力增大,如图4与图5所示,为双旋翼的“厚度效应”。此外,算例4相较于其他算例,上旋翼气动环境更为良好,该算例下的上旋翼拉力有所提升。下旋翼浸没于上旋翼产生的下洗流中,气动环境较上旋翼更为恶劣,下洗流引起下旋翼的有效工作迎角减小,因此下旋翼拉力通常小于上旋翼拉力。上下旋翼拉力波动幅度差异,主要由旋翼间“载荷效应”和“厚度效应”共同影响造成[15]。上下旋翼在相对旋转时,每个周期内的相互接近和远离过程中,旋翼桨叶前缘的附着涡对另一片旋翼桨叶产生的上洗作用会转变为旋翼桨叶后缘的附着涡对另一片旋翼桨叶产生的下洗作用,从而导致上下旋翼的相对迎角和拉力表现为先增大后减小的周期性波动,这种跟载荷相关的干扰现象则被称为“载荷效应”。在“厚度效应”的作用下,双旋翼拉力波动可以互相抵消削弱一部分,因此上下旋翼拉力和的波动幅度会有所减小。图6中,上下旋翼的拉力和也呈周期性变化,此模型的直升机重量为5 T,除了算例1和算例2,其他算例的拉力和均能满足重量的要求,同时还能提供一部分余量。
图7是算例3、算例4和算例5的上旋翼桨叶上下表面在方位角为360°时的压强分布云图,从图中可知,上旋翼上表面的压力随着总距差的增大而减小,由于算例4中上旋翼气动条件更为良好,其上表面的负压大于算例3和算例4,而下表面压力场与其他算例无明显区别,因此算例4上旋翼拉力更大。从图7中还能看出上面分析的旋翼“厚度效应”带来的影响,随着总距差的增大,上下旋翼间距减小,上旋翼的低压区减小,使得旋翼上下表面压差变大。

图7 上旋翼桨叶上下表面压力分布云图
上下旋翼转向相反,取上下旋翼力矩的绝对值分析旋翼力矩变化规律,如图8—图10所示。上下旋翼的力矩随总距差的变化规律与旋翼拉力变化情况相近,在此则不加赘述。

图8 上旋翼力矩变化曲线

图9 下旋翼力矩变化曲线
图10为不同总距差下,上下旋翼间力矩差(上旋翼力矩绝对值-下旋翼力矩绝对值)的变化情况,上下旋翼的力矩差值随总距差的增大而先减小再增大,若总距差大于-0.5°这一临界值,则力矩差为负。上述现象主要是“涡诱导效应”引起,由于双旋翼尾迹相互诱导,下旋翼受上旋翼产生的下洗流干扰,其有效工作迎角变小,若要达到上下旋翼力矩平衡,应增大下旋翼的总距角或者减小上旋翼的总距角来弥补力矩差,上下旋翼总距差应由翼型参数确定。

图10 上下旋翼力矩差变化曲线
图11给出了悬停状态下算例3、算例4和算例5的上下旋翼桨叶在方位角为360°时的诱导速度场(Vj)图,从中可以看到明显的“涡诱导效应”,其下旋翼桨盘的诱导速度明显大于上旋翼桨盘的诱导速度,由于上、下旋翼的相互诱导作用,上旋翼受到的上洗流也明显小于下旋翼受到的下洗流,在旋转速度一定的情况下其下旋翼的实际工作迎角变小,诱导功率更大,导致功率损失更大,所以必须增大下旋翼总距[16]。
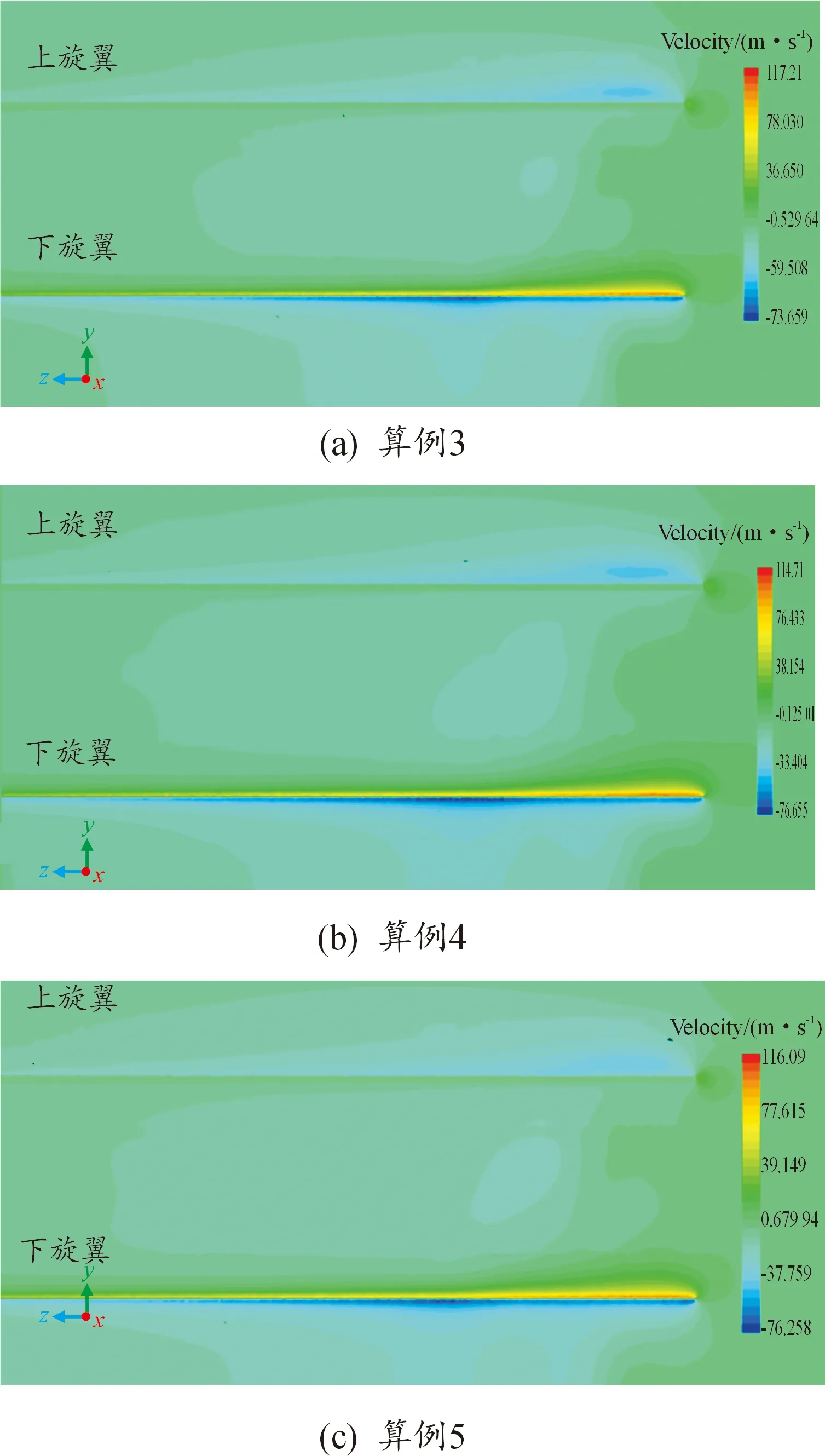
图11 双旋翼桨叶诱导速度场
一般的,在悬停状态下共轴式刚性双旋翼的上下旋翼总距角相差在1°以内,且上旋翼总距角总小于下旋翼总距角[16-18]。根据之前的分析,在上下旋翼相同的功率下,上旋翼的下洗流对下旋翼的干扰比下旋翼的上洗流对上旋翼的干扰更加强烈,正常工作时,下旋翼的诱导速度等于自身产生的诱导速度与上旋翼产生的下洗速度之和,下旋翼的诱导速度增大导致下旋翼桨叶剖面的有效工作迎角减小,若上下旋翼采用相同的总距角,则下旋翼产生的拉力和力矩更小,所以,必须使下旋翼的总距角大于上旋翼的总距角,才能平衡直升机的反力矩[19]。所以图12和图13是在5个算例的基础之上,插值拟合出的总距差在-1°~0°,上下旋翼平均拉力和力矩相关参数的变化情况。
上下旋翼平均拉力与力矩表达式:

(5)
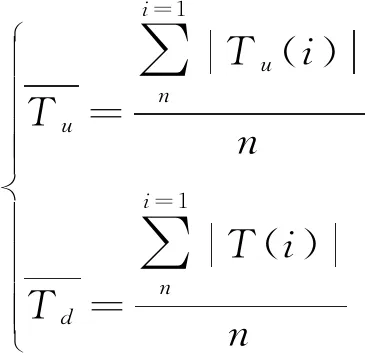
(6)
式中:Fu(i)与Fd(i)分别为i时刻上下旋翼拉力;n为一个周期内的步长数;Tu(i)与Td(i)分别为i时刻上下旋翼力矩。
图12中,随着上旋翼总距角的增大,上旋翼产生的下洗气流方向也因此改变,下旋翼气动条件改善,有效迎风角增大,因此下旋翼拉力逐步提升。上下旋翼的总距差增大,在总距差为 -0.25°时,由于上旋翼周围的气动条件更优,表现为算例4上旋翼产生的拉力高于其他算例。
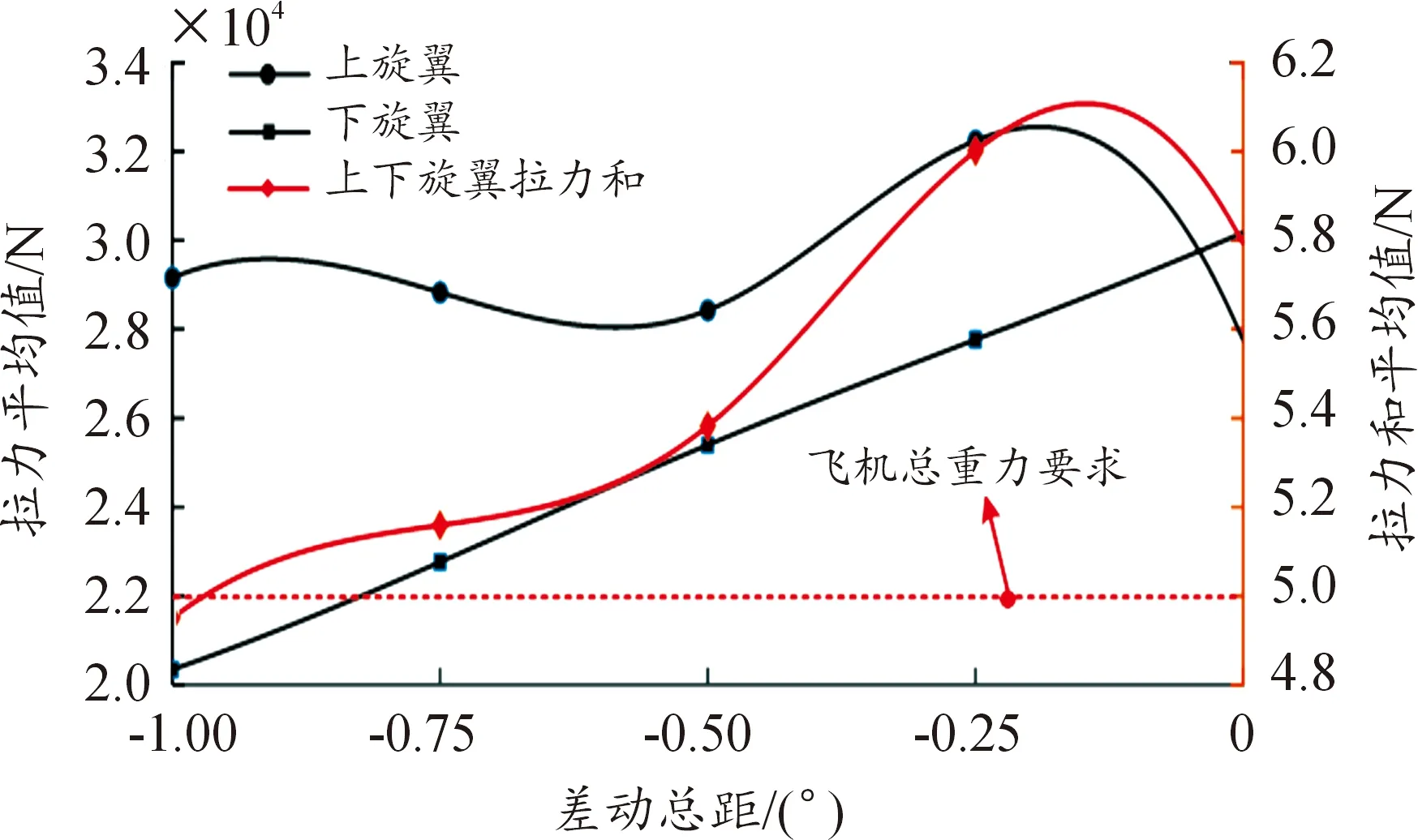
图12 上下旋翼拉力相关参数变化曲线
本文以上下旋翼力矩差系数来描述上下旋翼力矩在整个周期内的差异程度,“力矩差系数”越大,说明上下旋翼力矩波动越明显,双旋翼系统越不稳定。力矩差系数计算公式如下所示:
(7)
从图13中可以发现,随着总距差的变化,上下旋翼的力矩变化和拉力的变化情况类似,上下旋翼的力矩差系数存在最小的极值点。上下旋翼周期内平均力矩有3个交点,分别是A(-0.6,23 140)、B(-0.4,24 925)和C(-0.1,27 370)点,代表周期内的上下旋翼力矩平衡。3点中,B点对应的力矩差系数P(420.67)最小,选取力矩平衡点B的上下旋翼总距角作为力矩平衡的总距角。

图13 上下旋翼力矩相关参数变化曲线
以B点算例所代表的上下旋翼的总距角对上面的力矩平衡分析结论进行仿真验证,由图14和图15可以看出,在上下旋翼总距角为5.6°和6.0°的情况下,基本与上述分析吻合,实现上下旋翼的力矩平衡。悬停状态下,在一个稳定的运行周期内,上旋翼产生了更大的拉力,而上下旋翼产生的力矩相当,计算得到上旋翼的平均力矩为27 168 N·m,下旋翼的平均力矩为27 044 N·m,平均力矩差为124 N·m,上下旋翼的平均力矩差仅为上下旋翼平均力矩的0.46%,力矩差系数为470。

图14 B点算例上下旋翼拉力变化曲线

图15 B点算例上下旋翼力矩变化曲线
图16给出了上下旋翼总距角分别为5.6°和6.0°时计算得到的气动性能结果,图中可见,上下旋翼的气动载荷的计算值均较为正常,可以进一步将其作为直升机传动系统正向设计的输入。其中CT为共轴双旋翼拉力系数、CQ为共轴双旋翼扭矩系数,定义如下:

图16 配平状态下双旋翼的气动性能

(8)

(9)
式中:Fup和Flow分别为上、下旋翼拉力;Tup和Tlow分别为上、下旋翼力矩;ρ为海平面空气密度;Ω为旋翼转速;R为旋翼半径。
3 结论
1) 在共轴式刚性双旋翼悬停状态下,保持下旋翼总距角不变,随着共轴式双旋翼的总距差的增大,由于旋翼的“厚度效应”,上旋翼的拉力与力矩会先减后增再减小,下旋翼的拉力和力矩会一直增大。
2) 由于旋翼“载荷效应”和“厚度效应”的共同影响,双旋翼在相对旋转过程中,上下旋翼的拉力均会出现上下波动,且波动方向相反的现象,而且上旋翼的总距角越大,受“载荷效应”的影响越大。
3) 由于“载荷效应”与“涡诱导效应”的存在,共轴式刚性双旋翼拉力和力矩呈周期性变化,而且在变化过程中,下旋翼处在上旋翼的下洗流中,使下旋翼的实际工作迎角变小,下旋翼的气动性能降低,导致下旋翼的拉力比上旋翼小。
4) 根据本文的仿真分析与力矩平衡计算,在悬停状态下,上下旋翼力矩平衡时,下旋翼的总距角要大于上旋翼,本文中共轴式刚性双旋翼模型悬停下的最佳总距角为上旋翼5.6°,下旋翼6.0°,此时不仅能够实现上下旋翼的力矩平衡,而且其力矩波动系数最小。

