关于初中数学综合与实践教学的几点建议

竺雪婷

江苏省南京市栖霞区金陵中学仙林分校 210000

《义务教育数学课程标准（2011年版）》指出，数学课程教学应帮助学生积累数学活动经验，培养学生的应用意识与创新能力，以促进学生核心素养的生成［1］.因此，综合与实践课应以问题为引导，通过开展数学活动，使学生不断积累数学活动经验，提升学生的应用意识与创新能力.

教学中应凸显综合性与实践性

综合与实践课的综合性与实践性表现在以学生的现实生活和学习实践为素材，以学生的学与思为主要形式，凸显学生应用知识解决问题的能力，进而提升学生的核心素养.在整个过程中，学生运用多种方法和多种数学模型解决问题，既不是单一知识点的直接应用，也不是某种方法的简单模仿，而是创新性地解决问题.

“图形变换”问题是生产生活中很常见的一类问题.学生在学完“轴对称、平移与旋转”后，用图形变换的思想解决生活中问题，有利于调动学习的积极性，有利于积累数学活动经验，有利于提升问题解决的能力.

问题1：如图1，长方形台球桌ABCD上有两个球P，Q.（1）请画出一条路径，使得球P撞击台球桌边AB反弹后，正好撞到球Q；（2）请画出一条路径，使得球P撞击台球桌边，经过两次反弹后，正好撞到球Q；

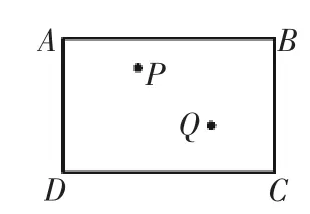
图1

问题2：如图2所示，在俄罗斯方块游戏中有一条重要的规则，即当某一行的小方格被填满时，这一行的小方格就会自动消失.图2中有三行的方格拼成了如图所示的形状，在屏幕的上方，一组方格正在向下移动，如何转动这组小方格，可以让屏幕最下方的所有小方格都填满消失呢？

图2

问题3：在南京市水环境质量整治中，运粮河栖霞区段河岸两边护坡上铺设了一种混凝土地砖，地砖的形状如图3所示，某施工单位运进了这种规格的混凝土地砖共10万块，那么这个施工队铺设了多少平方米的护坡呢？

图3

本节课的三个问题分别对应轴对称、旋转与平移在实际生活中的应用，问题1是轴对称在桌球运动中的应用，其实质仍是最短路径问题，解决问题的基本思想是化折为直.问题2是旋转和平移在游戏中的应用，揭示了全等变换只改变图形的位置，不改变图形的形状.问题3是平移在工程问题中的应用，利用平移可以将不规律图形化为规则图形，体现了数学中的转化思想.三个问题贴近学生生活实际，利于学生积极实践探索，提高了学生应用数学解决实际问题的能力，提升了学生的核心素养.

教学中应凸显学生的主体性

在综合与实践课教学中，教师应尊重学生的主体地位，以学生的自主探究为基础，在动手操作和合作交流中，让学生经历将实际问题转化为数学问题的过程，促使学生不断积累活动经验，体验由经历到获得的过程，从而体悟数学的价值.

相似三角形是从实际生活中抽象出来的数学模型，它在生活中有着广泛的应用，在学生学过“相似三角形”以后，笔者组织了一节别开生面的综合实践课.

实践任务：测量校园内旗杆的高度.笔者让数学课代表把任务分割后分给几个小组，要求学生在测量完成后，回教室计算，比较测量方法的优劣，总结测量与计算的得与失.

课代表指挥有方，学生行动迅速.30分钟过后，学生有了自己的方法与结果，然后学生回到教室整理自己的数据.最后，教师派小组代表写下自己的解决方案和结论.下面是一组学生的结果报告（见表1）.

表1

教学中，笔者敢于放手让学生通过自己的探究得到一手材料，然后通过计算得到结果，并鼓励学生展示自己的成果，培养了学生动手实践、自主探究与合作交流的能力，真正凸显了学生的主体地位，在应用数学解决问题的过程中，让学生积累了更多的数学活动经验，真正体会到数学的价值.

教学中应凸显问题的引领性

综合与实践课的载体是问题，这需要教师精心设计问题，引领学生与外部世界进行交流与融合，通过亲身参与探求未知世界.学生不仅要想一想，还要看一看、听一听、说一说、动一动，身体力行，全身心去感悟.教师在关注结果的同时，更要看重过程，引导学生积极活动，展现思维过程，交流实践经验与体会，进一步提升学生的创造能力［2］.

比如，学生在学完平行四边形后，笔者给学生上了这样一节综合与实践课：

问题1：如图4，平行四边形ABCD中，点E为AB边上一点，请用无刻度的直尺在CD 边上画出点F，使四边形AECF为平行四边形，并说明理由.

图4

问题2：请仅用无刻度的直尺在两个等边三角形和一个正方形拼在一起的图形中画图.（1）在图5中画一个60°的角，使点C或点E是这个角的顶点，且以CE为这个角的一边；（2）在图6中画一条直线AP，使得AP∥CE.

图5

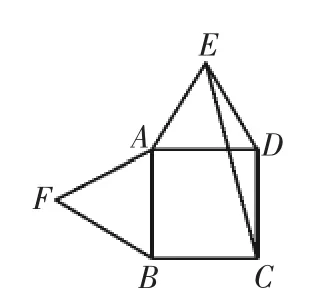
图6

问题3：如图7，已知矩形纸片ABCD，AD=15，AB=8，点E在边BC上，将纸片沿AE折叠，使点B落在点F处，连接FC，当△EFC是直角三角形时，求△EFC的面积.

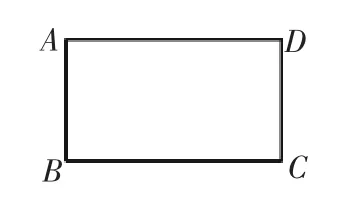
图7

本节课的三个问题，要求学生通过动手尝试，在不断的失败中总结成功的经验.第一个问题考查了平行四边形的性质，由于要求学生使用无刻度的直尺，所以学生必须先找到平行四边形的对称中心才能找到点F，学生在动手操作的过程中，体验了平行四边形的中心对称性.第二个问题考查了正方形与等边三角形的性质，学生可以与小组的其他同学交流，获取合理的建议，找到合理的解题路径.第三个问题考查了矩形的性质，学生可以按数据做一个纸片，在折叠的过程中，体验当△EFC是直角三角形时的两种情况.在实际操作的过程中，能促进学生积累活动经验.

总之，综合与实践课有利于培养学生数学探究能力，有利于培养学生数学应用能力，使学生发现数学的本质，感受数学的生活价值.基于此，广大数学教师应不断探索综合实践课的教学路径，以使全体学生都能获得不同程度的发展，在综合与实践课中学到有价值的数学.