具有标量旗曲率的闵可夫斯基积芬斯勒度量

田 畅，何 勇，李淑雯，张 辉

（新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017）

芬斯勒几何在自然学科领域应用广泛。研究具有特殊曲率性质的芬斯勒度量是芬斯勒几何中的重要课题之一。旗曲率作为芬斯勒几何中重要的黎曼几何量［1］，直接反映了芬斯勒空间的弯曲程度。芬斯勒几何中的旗曲率是黎曼几何中截面曲率的自然推广［2］，芬斯勒几何中的标量旗曲率是黎曼几何迷向截曲率的自然推广。旗曲率最早由贝瓦尔德［3-4］提出。

2003年，程新跃、莫小欢和沈忠民［5］证明了具有标量旗曲率的芬斯勒度量具有迷向S曲率。同年，沈忠民［6］证明了局部射影平坦芬斯勒度量一定具有标量旗曲率。2009年，沈忠民和Yildirim［7］得到了Randers度量具有标量旗曲率的充要条件。2013年，沈忠民和夏巧玲［1］构造出具有标量旗曲率的Randers度量。2014年，程新跃［8］证明了具有标量旗曲率的（α，β）-度量具有迷向S曲率。2016年，夏巧玲［9］证明了满足特定条件的局部射影平坦广义（α，β）-度量具有标量旗曲率。2018年，沈忠民和杨国军［10］证明了具有标量旗曲率的二次度量是局部射影平坦的。2021年，刘怀福和莫小欢［11］证明了局部射影平坦扭曲积芬斯勒度量具有常旗曲率。上述研究成果表明，研究具有标量旗曲率的芬斯勒度量具有十分重要的价值和意义。

1982年，Okada［12］首次给出了闵可夫斯基积芬斯勒度量的概念，并得到了闵可夫斯基积芬斯勒流形上的测地线与其分量流形上测地线之间的关系。2021年，栗嘉慧、何勇和田畅［13］研究了闵可夫斯基积芬斯勒度量的贝瓦尔德曲率和Landesberg曲率，并分别给出了闵可夫斯基积芬斯勒度量成为贝瓦尔德度量、弱贝瓦尔德度量、Landsberg度量和弱Landsberg度量的充要条件。

一个自然的问题是，若芬斯勒度量F1和F2的旗曲率消失，那么F1和F2的闵可夫斯基积芬斯勒度量F的旗曲率是否消失？类似地，若芬斯勒度量F1和F2均具有标量旗曲率，那么在什么条件下F1和F2的闵可夫斯基积芬斯勒度量F仍具有标量旗曲率。文章主要针对以上两个问题进行探究。

1 预备知识

定义1［14］光滑流形M上的芬斯勒度量是一个函数F:TM→ℝ+，满足

（i）G=F2在͂=TM{0}上C∞；

（ii）对任意的(x,y)∈͂，F(x,y)>0；

（iii）对任意的(x,y)∈͂，λ∈ℝ，有F(x,λy)=||λ F(x,y)；

定义2［15］芬斯勒度量F的黎曼曲率为其中

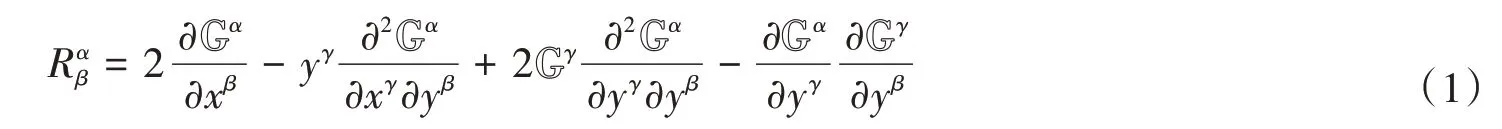
定义3［15］芬斯勒度量F的角度量为hy=hαβdxα⊗dxβ，其中

定义4［15-16］设F是一个芬斯勒度量，对一个包含切向量y的二维切子空间P=span{}y,u⊂TxM，旗曲率K定义为

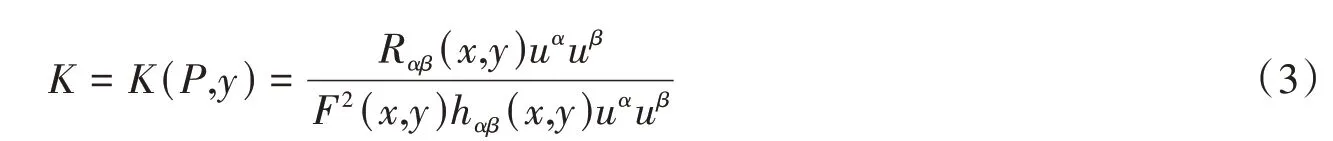
其中K(P,y)可以看作旗面P和旗杆y的函数，且

若F满足

则称F具有标量旗曲率K=K(x,y)，其中

设M1和M2分别是m维和n维光滑流形，那么乘积流形M=M1×M2是一个m+n维光滑流形。

设π1:M→M1和π2:M→M2表示自然投影，即∀x=(x1,x2)∈M，x1=(x1,…,xm)∈M1，x2=(xm+1,…，xm+n)∈M2，有π1(x)=x1和π2(x)=x2.

设dπ1:TM→TM1和dπ2:TM→TM2分别表示由π1、π2诱导的切映射，则∀(x,y)∈TM，(x1,y1)=(x1,…,xm,y1,…,ym)∈TM1,(x2,y2)=(xm+1,…,xm+n,ym+1,…,ym+n)∈TM2，有dπ1(x,y)=(x1,y1)和dπ2(x,y)=(x2,y2)，且有自然同构TM≅TM1⊕TM2.

定义5［12］设f：[0,+∞)×[0,+∞)→[0,+∞)是一个连续函数且满足

（1）f(s,t)=0当且仅当(s,t)=(0,0)；

（2）对于任意的λ∈[0,+∞)，有f(λs,λt)=λf(s,t)；

（3）f在(0,+∞)×(0,+∞)上是C∞函数；

（4）对于任意的(s,t)∈(0,+∞)×(0,+∞)，有

（5）对于任意的(s,t)∈(0,+∞)×(0,+∞)，有

则称f为积函数。

命题1［17］设f是积函数，则对任意的S≠0,T≠0有

其中，f的下标S和T分别表示对S和T求偏导数，如

定义6［12］设(M1,F1)和(M2,F2)是两个芬斯勒流形，f:[0,+∞)×[0,+∞)→[0,+∞)是积函数，记S=F21和T=F22.芬斯勒度量F1和F2关于f的闵可夫斯基积是在乘积流形M=M1×M2上赋予的如下形式的芬斯勒度量F:TM→ℝ+

其中(x,y)∈TM，x=(x1,x2)，y=(y1,y2).常简称F为闵可夫斯基积芬斯勒度量，称(M,F)是(M1,F1)和(M2,F2)关于f的闵可夫斯基积流形。

记G=F2，则G的基本张量矩阵为［13］

其中

文章小写希腊字母指标α，β，γ等变化从1到m+n；小写拉丁字母指标i，j，k等变化从1到m；带撇号的小写拉丁字母指标i′，j′，k′等变化从m+1到m+n.与F1或F2有关的几何量，分别在其正上方加指标“1”或“2”以示区别，如和分别表示F1或F2的黎曼曲率系数。

2 闵可夫斯基积芬斯勒度量的旗曲率

设F是芬斯勒度量F1和F2的闵可夫斯基积。本节将推导闵可夫斯基积芬斯勒度量F的黎曼曲率系数和旗曲率公式，并讨论若两个芬斯勒度量F1和F2的旗曲率均消失，那么F1和F2的闵可夫斯基积芬斯勒度量F的旗曲率是否消失。

引理1［13］设F是芬斯勒度量F1和F2的闵可夫斯基积，则由F诱导的喷射系数Gα为

命题2设F是芬斯勒度量F1和F2的闵可夫斯基积，则F的黎曼曲率系数Rα β为

证明令（1）式中α=i，β=j，将（16）和（17）式代入其中，可得

同理可证（19）和（20）式成立。

命题3设F是芬斯勒度量F1和F2的闵可夫斯基积，则

其中

证明令（4）式中γ=j，β=k，则有

将（12，14，18）和（20）式代入（29）式可得

令（30）式中fSSSiSj+fSSij=a1，则有

同理可证（22）~（24）式成立。

命题4设F是芬斯勒度量F1和F2的闵可夫斯基积，则F的角度量系数hαβ为

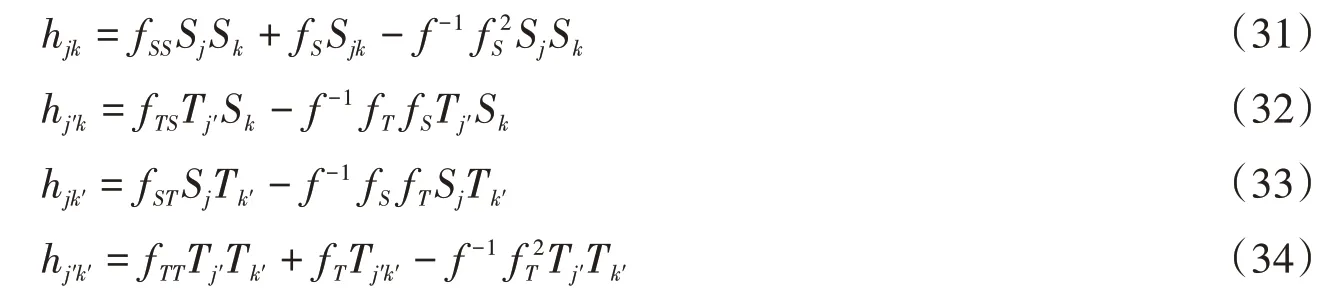
证明令（2）式中α=j，β=k，则有

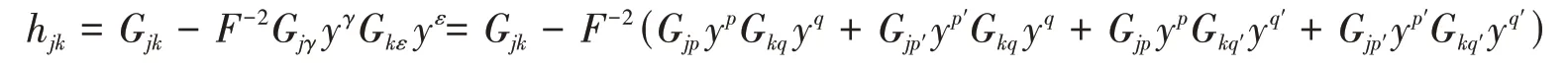
将（11）（12）和（14）式代入上式，经计算和整理可得

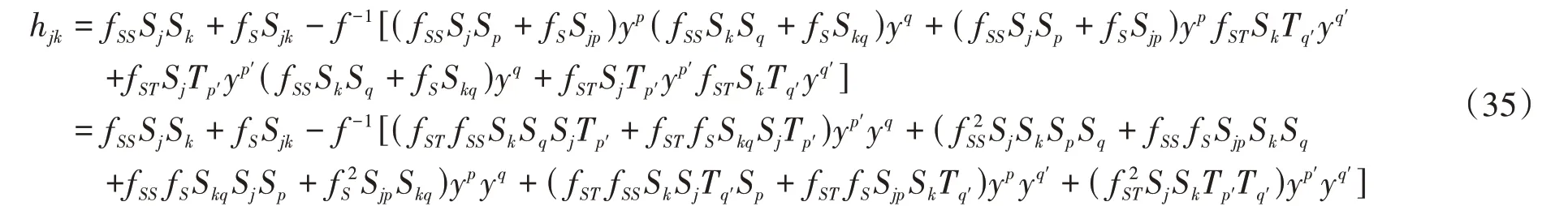
由于S=F21和T=F22关于y都是2次齐次的，根据欧拉定理，有

将（36）式代入（35）式，经直接计算可得

将（8）式代入（37）式，可得

同理可证（32）~（34）式成立。

定理1设F是芬斯勒度量F1和F2的闵可夫斯基积，则F的旗曲率为

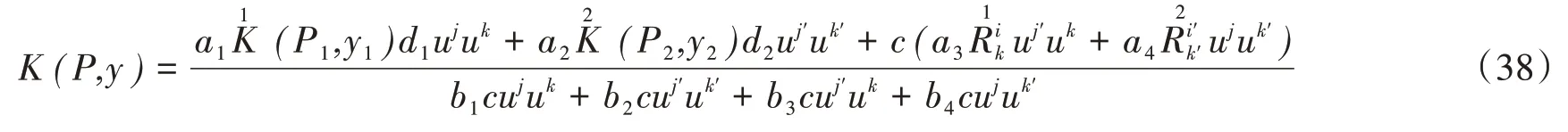
其中

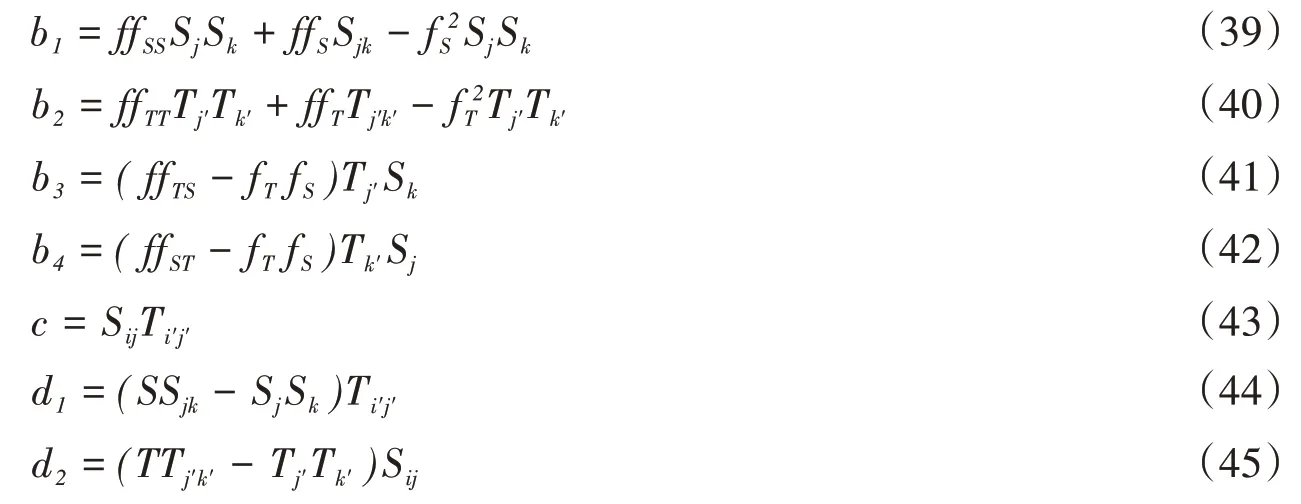
证明根据（3）式有

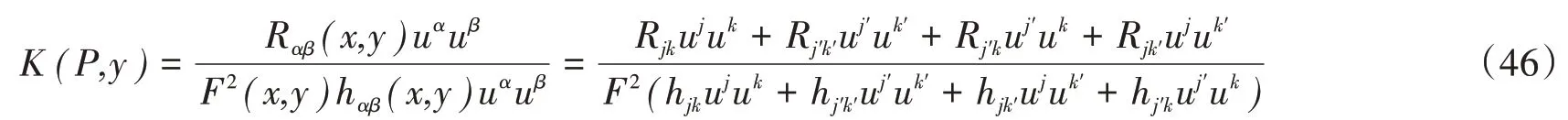
将（21）~（24）式代入（46）式，可得

由（11）式和（31）式可得

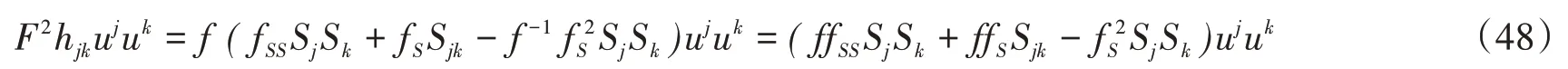
令（48）式中ffSSSjSk+ffSSjk-f2S SjSk=b1，则有

同理可得

将（49）~（52）式代入（47）式可得

对芬斯勒度量F1应用（3）式，并注意到F21=S，可得F1的旗曲率为

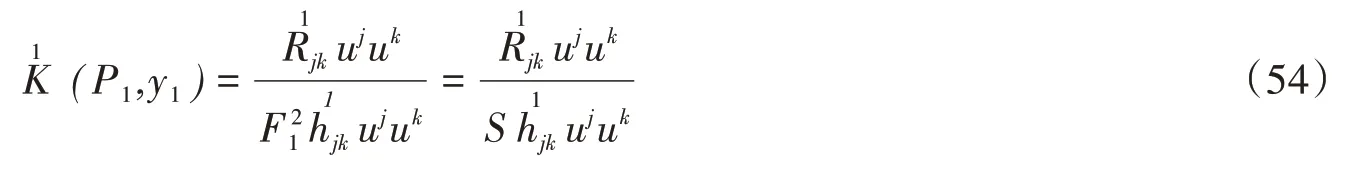
将（4）和（2）式代入（54）式可得

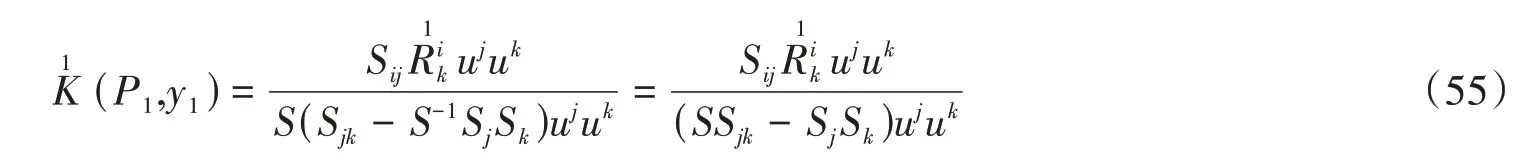
同理可得F2的旗曲率为

对（55）和（56）式变形可得

将（57）和（58）式代入（47）式，经化简可得（38）式成立。证毕。

定理2设F是芬斯勒度量F1和F2的闵可夫斯基积，且芬斯勒度量F1和F2的旗曲率消失，则F的旗曲率消失当且仅当

证明芬斯勒度量F1和F2的旗曲率消失当且仅当

根据（60）及（38）式可知，K(P,y)=0等价于

由于(Sij)和(Ti′j′)可逆且不为0，因此c=SijTi′j′≠0，所以（61）式等价于

将（27）和（28）式代入（62）式可得

下面先证必要性，（63）式两边与yiyi′yjyj′缩并，可得

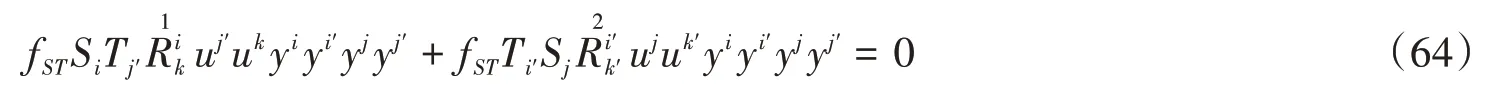
将（36）式中第3和第4个等式代入（64）式可以得到

由于fST≠0,S≠0,T≠0，因此上式等价于（59）式。

再证充分性，（59）式两边与yiyi′yjyj′缩并可得

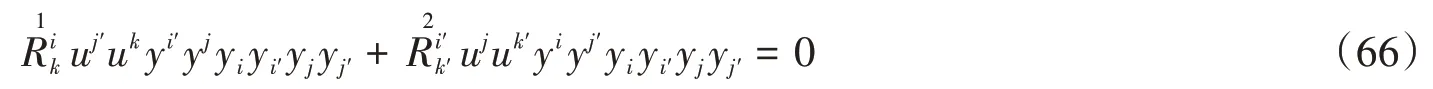
令yi=Gij′yj′，根据（14）式，则有

因此

再将（36）式中第3、4个等式代入（68）式可得

将（69）式代入（66）式，则有

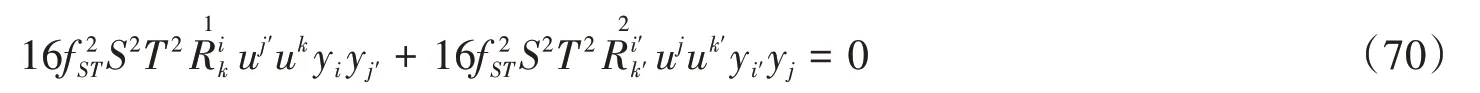
由于16f2ST≠0,S2≠0,T2≠0，上式等价于

将（67）式代入（71）式，可得

应用（36）式中第3和第4个等式，（72）式等价于

由于fST≠0,S≠0,T≠0，因此可得（63）式成立。定理得证。

3 具有标量旗曲率的闵可夫斯基积芬斯勒度量

设F是芬斯勒度量F1和F2的闵可夫斯基积，且F1和F2均具有标量旗曲率。本节将探索给出F具有标量旗曲率将满足什么样的微分方程刻画。

命题5设F是芬斯勒度量F1和F2的闵可夫斯基积，则

证明令（6）式中α=i，β=j将（12）和（14）式代入，并注意到（11）式，则有

其中，在第四个等式的推导中用到（36）式中的Skyk=2S,Sjkyk=Sj,Tk′yk′=2T，第五个等式的推导中用到（8）式的变形，即fSSS=-fSTT.同理可证（75）~（77）式成立。

定理3设F是芬斯勒度量F1和F2的闵可夫斯基积，且F1和F2的具有标量旗曲率，则F具有标量旗曲率当且仅当下列方程组成立

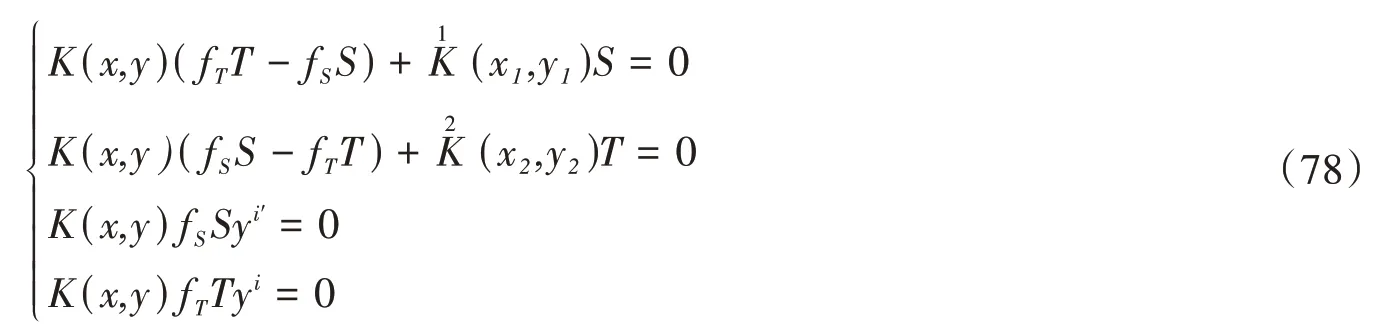
证明对于芬斯勒度量F1应用（6）式有

将（36）式中的第1个等式代入（79）式，并注意F21=S，则有

根据定义4可知，芬斯勒度量F1具有标量旗曲率当且仅当

将（80）式代入（81）式，并注意F21=S，可得

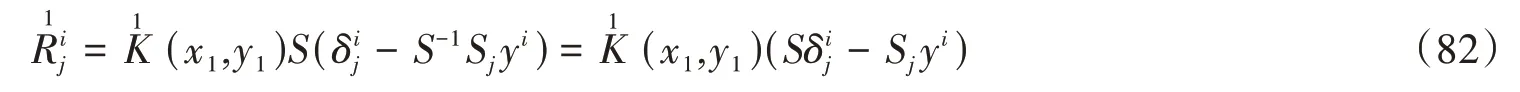
同理可得，芬斯勒度量F2具有标量旗曲率当且仅当

根据定义4，芬斯勒度量F具有标量旗曲率等价于下列方程式成立

将（18）~（20）式代入上述方程组，可得

将（82）和（83）式代入方程组（85）式有

由（11）和（74）式可得

同理可得

将（87）~（90）式代入（86）式，可得下列方程组

对方程组（91）式的第一个和第三个等式两边与yj缩并，第二个与第四个等式两边与y j′缩并，并应用（36）中第3和第4个等式，经化简可得方程组（78）.定理得证。

4 结论

文章给出了两个旗曲率消失的芬斯勒度量F1和F2的闵可夫斯基积芬斯勒度量F的旗曲率消失的充要条件。得到了两个具有标量旗曲率的芬斯勒度量F1和F2的闵可夫斯基积芬斯勒度量F具有标量旗曲率的微分方程刻画。这为构造具有消失旗曲率的芬斯勒度量及构造具有标量旗曲率的芬斯勒度量提供了新的途径。后期将在此基础上通过求解复杂的微分方程，构造出具有消失旗曲率的芬斯勒度量或具有标量旗曲率的芬斯勒度量具体例子。