基于Isight的板簧式起落架参数优化

刘炎辉，张 毅，李富刚

(中国飞行试验研究院，陕西 西安 710089)

1 引言

起落架是飞机关键的组成部分，飞机的事故有50%以上发生在起飞和着陆阶段[1]。因此起落架的设计对于整架飞机的安全及性能有着至关重要的影响。缓冲器是飞机起落架必须具备的结构，板簧式起落架因其简单性、可靠性和维护性在小型、轻型飞机上被广泛使用[2]。随着现代无人机的发展，这种形式的缓冲器得到了越来越广泛的应用[3]。

传统的板簧式起落架的设计过程是一个反复迭代的过程，在设计过程中需要反复调整板簧式起落架的尺寸以使得起落架的变形和过载满足设计要求，在设计的过程中，往往需要进行多次试验，所需成本较大[4]。虚拟样机技术及参数优化理论的发展为解决这类问题提供了思路。利用多体动力学仿真软件如Virtual.lab、Adams进行板簧式起落架几何和尺寸约束的构建并对其进行落震仿真[5， 6]，将仿真计算所得结果通过程序输入Isight中，Isight根据输入结果及NSGA-Ⅱ优化算法生成的新设计点并通过程序返回Virtual.lab中，程序根据新的设计点对Virtual.lab中的模型进行更新和仿真计算，由此完成一轮迭代循环[7-10]。经过反复迭代循环可以完成板簧式起落架参数优化。基于Isight的参数化优化使得板簧式起落架设计过程中的反复迭代及试验工作都可以由程序完成，节约设计时间，降低试验成本。参数化优化流程如图1所示。

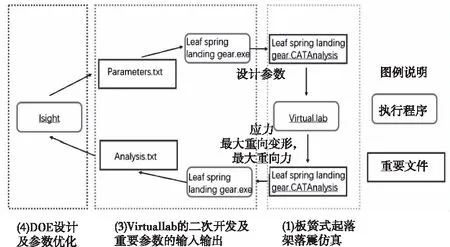
图1 板簧式起落架参数优化流程

2 板簧式起落架参数化建模

参数化设计利用几何约束和尺寸约束构建产品或零件的结构特征，搭建几何约束集。通过一系列的分析计算，可以从中找出对用户重要的约束并对其进行修改。在某约束被修改的同时，其他相关联的约束也会经过一定的计算更新，从而生成新的参数化模型。

在Virtual.lab中建立板簧式起落架参数模型，板簧式起落架重要参数可由数据表进行更新，从而可以作为优化的设计变量。板簧式起落架参数模型如图2所示：

图2 板簧式起落架参数化模型

板簧式起落架设计变量如图3所示。

图3 板簧式起落架设计变量

3 板簧式起落架落震仿真与试验验证

3.1 板簧式起落架落震试验

板簧式起落架落震试验台如图4所示。

图4 板簧式起落架落震试验台

板簧起落架落震试验投放质量计算如式(1)所示

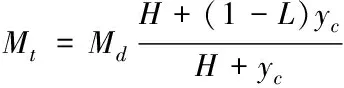
(1)

Mt为投放质量；Md为当量质量；L为升力系数；yc为上、下部质量总位移；H为投放高度。

轮胎转速计算如式(2)所示

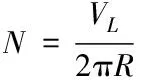
(2)

N为机轮预转速；VL为飞机着陆速度；R为机轮半径。板簧式起落架落震试验工况及试验结果如表1所示：

表1 板簧式起落架落震试验工况及试验结果

从表1中可以看出，随着投放高度增加，板簧式起落架最大垂向力与最大垂向变形均增大；缓冲效率无明显变化且变动幅度小于3%。相对于机轮不带转，当机轮存在初始角速度时，板簧式起落架落震时最大垂向力减小，最大垂向变形增大，缓冲效率降低。板簧式起落架落震试验如图5所示。

图5 板簧式起落架落震试验

3.2 板簧式起落架非线性落震仿真模型

板簧式起落架落震模型由Virtual.lab中的motion 求解器与mecano求解器进行耦合非线性求解。模型动力学方程由刚体系统动力学方程和非线性柔性体动力学方程组成。刚体系统动力学方程如式(3)、(4)所示

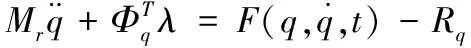
(3)

Φ(q，t，a)=0

(4)

(6)

其中M11，C11，K11分别为刚性界面处质量矩阵，阻尼矩阵和刚度矩阵；M22，C22，K22分别为非刚性界面处质量矩阵，阻尼和刚度矩阵；M12，C12，K12，M21C21，K21为刚性界面与非刚性界面的交叉项；δ1(t)为刚性界面处有限元单元节点坐标；δ2(t)为非刚性界面处有限元单元节点坐标；R为刚性界面处柔性体对刚形体作用力；P为非刚性界面处柔性体对刚性体作用力。

3.3 板簧式起落架仿真试验对比

以下落高度460mm(对应接地速度3m/s)，机轮预转速1980r/min这一工况为例，非线性仿真的应力应变云图如图6所示。

图6 板簧式起落架非线性仿真应力应变云图

作出板簧式起落架试验与非线性仿真垂向力与吊篮垂向位移随时间变化图。其中垂向力随时间变化图如图7所示。

图7 板簧式起落架落震试验垂向力随时间变化图

由图7可得，板簧式起落架非线性仿真最大垂向力误差为3.9%。

吊篮垂向位移随时间变化图如7所示。

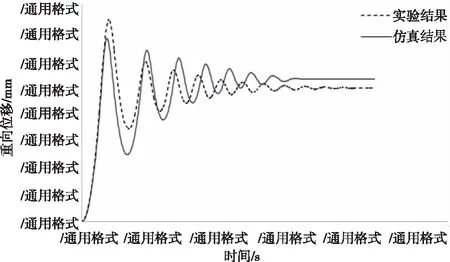
图8 板簧式起落架落震试验吊篮垂向位移随时间变化图

由图7可得，板簧式起落架非线性仿真最大垂向力误差为9.2%。

4 拉丁超立方试验设计

试验设计方法(DOE)提供了合理而有效地获得信息数据的方法，在工程和科研中有着广泛的应用，是当今产品开发、过程优化等环节中最重要的统计方法之一。拉丁超立方设计为试验设计的一种，有着较好的空间填充能力，较宽松的水平值分级及较好的非线性拟合能力。采用拉丁超立方设计探究板簧式起落架重要参数对质量及落震效率的影响。

1)设计变量

根据图3板簧式起落架参数模型中的重要参数，选定设计变量为参数为A1，A2，H1，H2，L1，L2，R1，R2，T。设计变量如式(7)所示

X=[A1，A2，H1，H2，L1，L2，R1，R2，T]

(7)

其中X为设计变量可行域。

2)约束条件

以结构最大应力为优化数学模型的约束条件，约束条件可表示为

(8)

其中λ为安全系数，此处取1.2；σm为板簧式起落架落震过程中最大应力；σs为材料许用应力；U1，U2为设计变量的上下限，其值大小根据，根据约束条件、板簧式起落架空间结构限制以及企业提供的技术参考确定。

3)目标函数

以板簧式起落架质量最小和效率最高为目标函数

(9)

其中，m(X)为质量目标函数；e(X)为落震效率目标函数。质量与效率的权重比为10：1。

4.1 设计变量对板簧式起落架质量的影响

作出设计变量对板簧式起落架质量影响的pareto图，如图9所示。

图9 设计变量对板簧式起落架质量的pareto图

从图9可以看出因子T对板簧式起落架质量影响最大。L1， H1，L2和H2其次。其余因子A1，R1，A2，H1-T的交叉项，L1-T的交叉项对板簧式起落架质量影响较小。各因子对质量的响应均为正效应。

4.2 设计变量对板簧式起落架落震效率的影响

作出设计变量对板簧式起落架落震效率影响的pareto图，如图10所示。

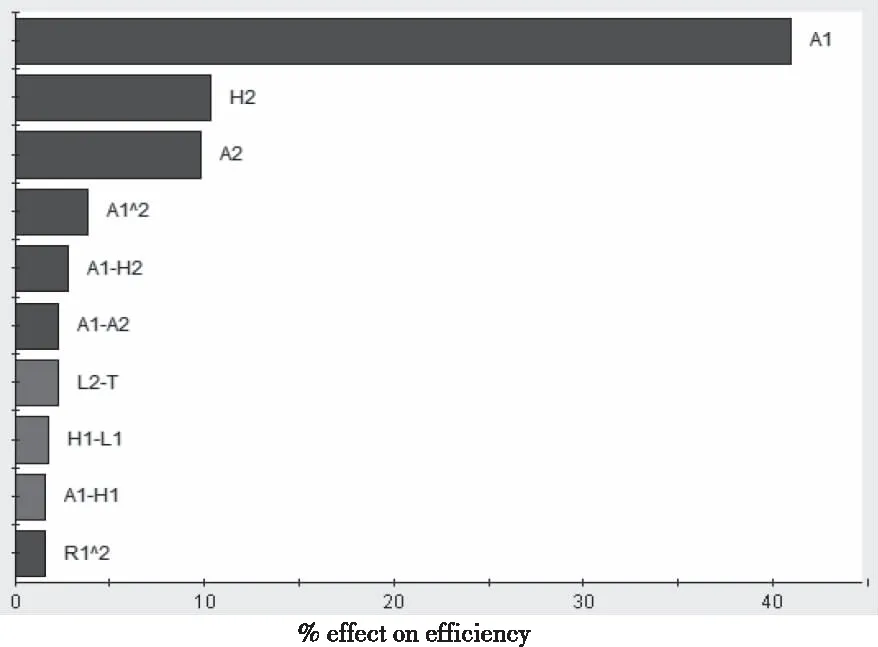
图10 设计变量对板簧式起落架落震效率的pareto图

从图10中可以看出因子A1对板簧式起落架落震效率影响最大，其次为H1和A2。其余A1的二次项，A1-H2的交叉项，A1-A2的交叉项，L2-T的交叉项，H1-L1的交叉项，A1-H1的交叉项，R1的二次项对板簧式起落架落震效率影响较小。

在有一个或几个因子的多水平作出设计变量对板簧式起落架落震效率影响的主效应图，如图11所示。

图11 设计变量对板簧式起落架落震效率的主效应图

5 NSGA-Ⅱ优化算法

NSGA-Ⅱ属于非归一化算法，其特点为一次性求得pareto前沿。NSGA-Ⅱ导入了“拥挤距离”和“拥挤距离排序”法，在具有同样的Pareto顺序层内，对个体进行排序。进化中，亲代群体进行交叉以及变异等运算得到子代，将两个群体合并。通过Pareto最优原则将群体中的个体进行两两比较，并将个体依次排序成多个前沿层，同一前沿层中具有更大拥挤距离的个体更优。在Isight中采用NSGA-Ⅱ算法对板簧式起落架进行优化。优化过程中板簧式起落架质量随迭代次数的响应如图12所示。

图12 质量随迭代次数的响应

板簧式起落架落震效率随迭代次数的响应如图13所示。

图13 落震效率随迭代次数响应

图12和图13中的黑点表示迭代过程中的可行域，红点表示不可行域，最终定格的绿点表示最终优化的最优结果。

设计点相对于板簧式起落架质量的三维散点图如图14所示。

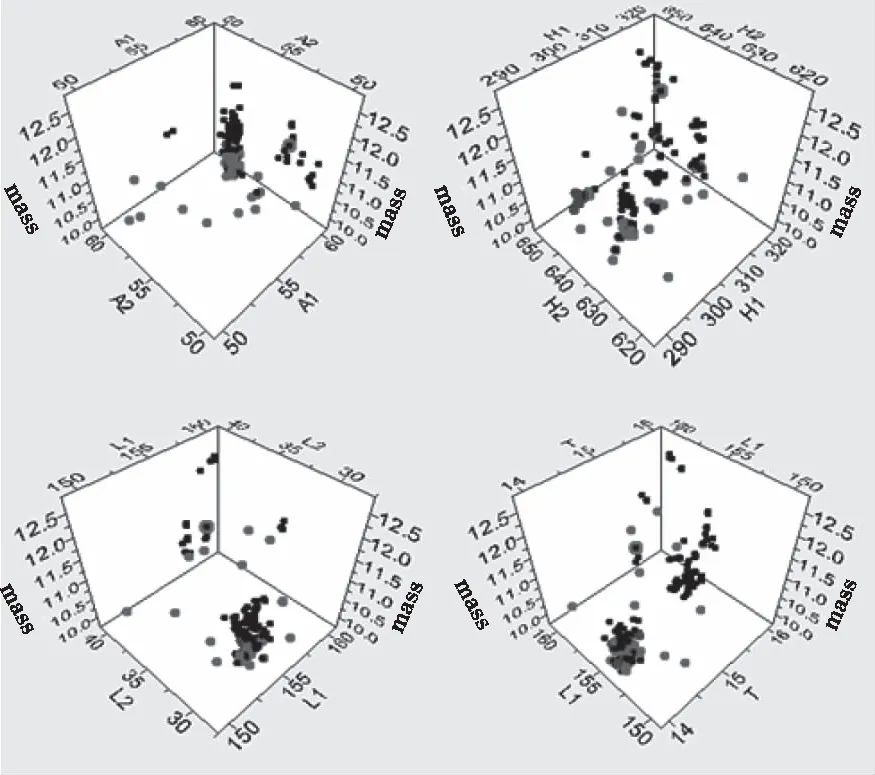
图14 设计点相对于板簧式起落架质量的三维散点图

设计点相对于板簧式起落架落震效率的三维散点图如图15所示。

图15 设计点相对于板簧式起落架落震效率的三维散点图

从图14、图15中可以看出，NSGA-Ⅱ算法的设计点较多，计算时长较序列二次规划长了很多。但设计点覆盖了整个设计空间，不易陷入局部最优解。且设计点在最优解附近分布较为密集，计算结果较为精确。将优化结果整理至表2中。

表2 板簧式起落架参数优化结果

从表2中可以看出，优化后板簧式起落架质量从11.68kg减少至9.92kg，减少了15.1%；效率从0.45增长至0.54，增长了20.0%，优化效果较为明显。

6 结束语

1)随着投放高度增加，板簧式起落架最大垂向力与最大垂向变形均增大；缓冲效率无明显变化且变动幅度小于3%。相对于机轮不带转，当机轮存在初始角速度时，板簧式起落架落震时最大垂向力减小，最大垂向变形增大，缓冲效率降低。

2) motion 求解器与mecano求解器耦合非线性求解能较好的模拟板簧式起落架落震过程。最大垂向力误差小于3.9%，最大垂向位移误差小于10%。

3)设计变量T、L1、H1、L2对板簧起落架质量影响较大。设计变量A1、H2、A2对板簧式起落架效率影响较大。

4) NSGA-Ⅱ优化算法优化效果较为明显，优化后板簧式起落架质量减少了15%，效率增加了20%。