煤岩基质-裂隙相互作用下渗透特性研究

王 斌，李波波，2，3，许石青，高 政，许 江，张 尧，陈 帅

（1.贵州大学 矿业学院，贵州 贵阳 550025；2.贵州大学 喀斯特地区优势矿产资源高效利用国家地方联合工程实验室，贵州 贵阳 550025；3.贵州省非金属矿产资源综合利用重点实验室，贵州 贵阳 550025；4.重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400044）

0 引 言

煤层气是煤矿开采一种重要的资源[1]，但我国的煤层气储层具有高吸附、低孔隙率、低渗透和高地应力的特点，严重制约了煤层气开采效率。渗透率用来表征煤层运输流体能力，也是评价瓦斯抽采效率的重要参数[2]。随着开采技术的不断成熟[3]，地下开采深度增加，应力和温度不断增加。因此，研究应力、温度和气体压力作用下煤岩孔裂隙结构、裂隙压缩性与渗流特性对煤层气开采具有重要意义。

为研究煤层气开采过程中煤岩渗透率演化规律，众学者开展了一系列煤岩孔裂隙结构、气体压力、温度、滑脱效应对渗透率影响的研究。传统的几何方法无法表征煤岩非均质性，利用分形维数定量表征煤岩微观孔隙发育已成为研究目标[4]。SEIDLE等[5]研究表明裂隙压缩性系数很难从现场获得，较多在实验室运用间接法测量。东振等[6]利用甲烷和氮气研究基质收缩、滑脱效应对渗透率的影响，结果表明气体压力越低，基质收缩和滑脱效应对渗透率的提升作用越明显。孙光中等[7]认为当外部应力恒定时，随着温度升高渗透率呈负指数下降。P&M模型[8]是基于孔隙率研究模型的代表，综合考虑有效应力、基质收缩对渗透率的影响，建立了孔隙率相关渗透率模型。TENG等[9]围绕温度对煤岩变形的影响建立了热敏渗透率模型，用于表征温度变化下煤岩-气体相互作用。此外，煤岩基质-裂隙相互作用认为基质与裂隙间存在“岩桥”连接[10]。因此，基质变形并非完全转化为裂隙变形。LU等[11]采用f变形修正系数（0～1）来表示基质吸附体积和裂隙吸附体积的变形增量，但并未揭示气体压力变化时煤岩内部有效内膨胀变形的不均匀分布。

综上所述，考虑应力作用下毛细管分形特征，建立裂隙体积应力敏感性模型。在温度作用下研究煤岩基质-裂隙相互作用，结合裂隙压缩性对渗透率的影响，进一步构建考虑煤基质内部膨胀变形、温度及气体压力变化的煤岩渗透率模型，并采用试验进行合理性验证，为煤层气抽采提供理论支撑。

1 应力与温度综合作用的渗透率模型

1.1 裂隙孔径分形特征

分形几何用于描述自然界不规则的现象[12]。煤岩中累积裂隙数目和直径可用分形标度表示为

（1）

式中：Np为累积裂隙数目；λp和λp,max分别为裂隙直径和最大裂隙直径，μm；Df为裂隙直径大小的分形维数；l为尺度，μm。

煤岩中裂隙直径大小的分形维数随温度而改变[9]，温度、裂隙直径大小的分形维数存在以下线性关系：

Df=Df0+η（ΔT/T0）

（2）

式中：Df0为初始温度下裂隙直径大小的分形维数；η为分形敏感系数；ΔT为温度变化量，K；T0为初始温度，K，本文T0取303 K。

考虑应力影响后，无应力状态下λp0到λp0+dλp0区间内煤岩总裂隙的数目、弯曲毛细管的实际长度Lp0分别表示为：

-dNp=Dfλpmax0Dfλp0-（Df+1）dλp0

（3）

Lp0（λ）=λp01-DTL0DT

（4）

式中：λp0和λpmax0分别为无应力状态下裂隙直径和最大裂隙直径，μm；L0、Lp0为弯曲毛细管的直线长度和实际长度，μm；DT为迂曲度分形维数。

1.2 裂隙体积应力敏感性模型

众多研究表明裂隙压缩性系数很难从现场获得，较多在实验室运用间接法测量。根据裂隙压缩性系数的定义可得煤岩裂隙总体积与应力间关系[5]为

（5）

式中：cf为裂隙压缩性系数；Vf为煤岩裂隙总体积，m3；σeff为有效应力，MPa。

当外部应力沿径向方向施加于煤岩时，弯曲毛细管侧面发生收缩并产生径向延展，弯曲毛细管的实际长度Lp、裂隙直径λp可表示[13]为

λp=（1-σeff/E）λp0

（6）

Lp=（1+σeffν/E）Lp0

（7）

式中：E为弹性模量，MPa；ν为泊松比。

三维立体空间下考虑应力影响的煤岩裂隙分形总体积可表示[14]为

（8）

将式（6）、式（7）代入式（8）中，可得应力作用下煤岩裂隙总体积为

（9）

1.3 考虑温度影响的煤岩变形特征

1）考虑温度影响的煤岩吸附变形，利用指数形式的修正系数对Langmuir方程进行修正，可得温度变化下修正的气体吸附量[9]为

（10）

式中：V为瓦斯吸附量，cm3/g；VL为吸附体积常数，cm3/g；p为气体压力，MPa；PL为Langmuir压力，MPa；c1和c2为温度修正项中的压力系数。

相应地，温度作用下气体吸附引起的吸附变形量为

（11）

式中：p0为初始气体压力，MPa；εL为最大膨胀变形量，取值为0.023。

2）温度引起的膨胀变形，温度引起的膨胀变形量εTe与温度之间呈如下线性关系[9]为

εTe=αTΔT

（12）

式中：εTe为温度引起的膨胀变形量；αT为热膨胀系数，K-1。

1.4 煤岩渗透率模型

当气体分子在孔径较小的管道中流动时，会产生“滑动”现象，导致气测值较大[15]。因此，考虑滑脱效应的渗透率可以表示成

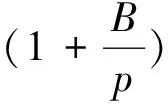
（13）

式中：k∞为煤岩绝对渗透率，10-3μm2；B为气体滑脱因子。

假设温度作用下产生的热膨胀/收缩和吸附引起的膨胀/收缩是各向同性的，则非等温煤岩体的应力应变的本构关系[16]为（压缩为负）

（14）

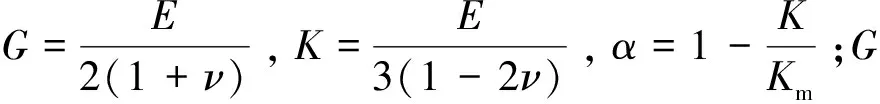
式（14）经过化简可得

（15）

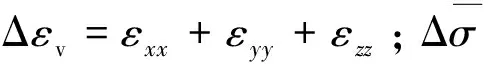
煤岩内部基质和裂隙之间的气体传输将引起内部膨胀变形[17]。在下文中，孔隙度的计算仅考虑了裂隙，并未考虑基质中孔隙的影响。假设煤岩总体积Vc等于裂隙体积Vf和基质体积Vm之和，则煤岩孔隙率定义为：Φ=Vf/Vc。因此，可将煤岩总体积、裂隙体积变化表示为

（16）

（17）

式中：γ=1-Kf/Km；Kf为裂隙模量，MPa；εin为煤基质内部膨胀变形量。

通过整理式（16）、式（17），可得

（18）

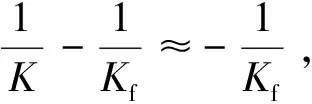
（19）

基于文献[18]的理论成果，考虑温度引起的吸附变形和热膨胀的影响，进一步研究煤基质内部膨胀变形特征及其对渗透率的影响。结合式（11）、式（12），煤基质内部膨胀变形可表示为

εin=βC（Δεs+ΔεTe）

（20）

（21）

（22）

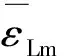
综上所述，考虑煤基质内部膨胀变形、温度变化以及气体压力变化的煤岩孔隙率模型为

（23）

基于立方定律[8]，进一步考虑滑脱效应影响，煤岩渗透率可表示为：

（24）

2 试验方法

2.1 等温吸附试验

为探究不同温度、气体压力下煤岩吸附特性，试验选取CH4作为试验气体，在0.1～5.0 MPa设定5个吸附平衡点，分别进行30、35、40、45、50 ℃下的等温吸附试验。试验装置为HCA型高压容量法吸附装置。依据GB/T 1960—2004，选取破碎至60～80目（0.177～0.25 mm）的煤岩进行试验，试验步骤为：气密性检查→抽真空→测定自由空间体积→等温吸附试验。

2.2 三轴渗流试验

为探究气体压力和温度综合作用下煤岩吸附与渗流特性，选取山西晋城赵庄煤矿3号煤层进行试验。原煤试件利用水泥浇筑法[19]制成，试验选用CH4气体，进行不同温度下（30、40、50、60和70 ℃）有效应力恒定气体压力升高的三轴渗流试验。试验装置采用含瓦斯煤热流固耦合三轴伺服渗流装置[25]。试验中气体压力控制为0.20、0.35、0.50和0.65 MPa。试验方案见表1。

表1 不同温度下气体压力升高的渗流试验方案

3 试验结果与模型验证

3.1 不同温度下煤岩吸附特性

将上述等温吸附试验数据代入式（10）中，得到不同温度下（303、308、313、318和323 K）煤岩气体吸附量（图1）。

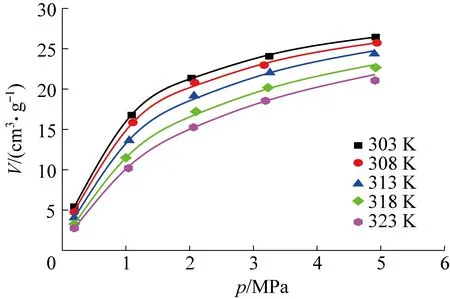
图1 等温吸附曲线Fig.1 Isotherm adsorption curve

由图1可知：利用修正后的Langmuir模型计算的模型值与试验值拟合度较好，在等温吸附试验的5个温度下，随着气体压力升高，煤岩气体吸附量逐渐增大，但其吸附速度呈下降趋势。当气体压力增至4 MPa时，吸附量曲线的斜率趋于平缓，此时煤岩吸附瓦斯量已近饱和状态。此外，当温度从303 K增加至313 K以及从313 K增加至323 K过程中，在相同压力下煤岩气体吸附量下降的平均值分别为2.2 cm3/g和3.1 cm3/g。即当温度逐渐升高时，瓦斯吸附量呈下降趋势。究其原因，温度升高会增加储层中气体分子的活性和动能，增加了气体在煤岩表面吸附的难度，降低其吸附能力。

3.2 不同温度和气体压力条件下的煤岩渗透特性

为验证新建渗透率模型的精确性，将不同温度、气体压力的CH4渗流试验数据代入式（24）中，可得不同温度下气体压力升高的渗流模型曲线，由图2可知：

1）新建渗透率模型值与渗流试验值相贴合，在相同的温度下，随着CH4入口压力的增大，煤岩渗透率呈先急剧下降后趋于平缓的趋势。以温度为303 K为例，气体压力由0.2 MPa上升至0.65 MPa时煤岩渗透率下降比例分别46.61%、7.50%、4.82%。这是由于随着气体压力逐渐升高，煤岩吸附能力增大，表面吸附层加厚。在外部应力的限制下，煤岩产生内部膨胀变形，气体渗流通道逐渐减少，因而渗透率不断降低。此外，滑脱效应在气体压力较低时其影响不容忽视，但随着气体压力的逐渐增大，滑脱效应不断减弱甚至消失[6]。随着气体压力的进一步增大，煤岩吸附变形量也逐渐达到饱和，因而渗透率下降趋势逐渐平缓。

2）此外，随着气体压力的逐渐增大，煤岩有效内膨胀变形的不均匀分布系数β不断减小。煤岩基质膨胀变形可以分成靠近孔裂隙的变形和远离孔裂隙的变形，其中靠近孔裂隙的膨胀变形决定着煤岩渗透率大小。当气体压力从0加载至0.2 MPa时，孔裂隙周围产生基质变形，使得孔裂隙变窄，这就进一步验证了气体压力较低时渗透率急剧下降的趋势。随着气体压力逐渐增大，孔裂隙周围基质膨胀对孔裂隙开度的影响逐渐减弱，β逐渐减小，渗透率减缓速度趋于平缓。

图2 渗透率、内膨胀系数与气体压力的关系（303 K）Fig.2 Relationship between permeability, internal expansion coefficient and gas pressure （303 K）

3.3 试验比较

为进一步验证新建裂隙体积应力敏感性模型和渗透率模型的适用性，根据许江等[18]赵庄矿试验数据，通过式（5）、式（9），计算得到1、2.5、4.0和5.5 MPa下煤岩裂隙压缩性系数cf，并通过式（24）计算不同有效应力条件下气体压力升高的渗透率变化曲线（图3）。

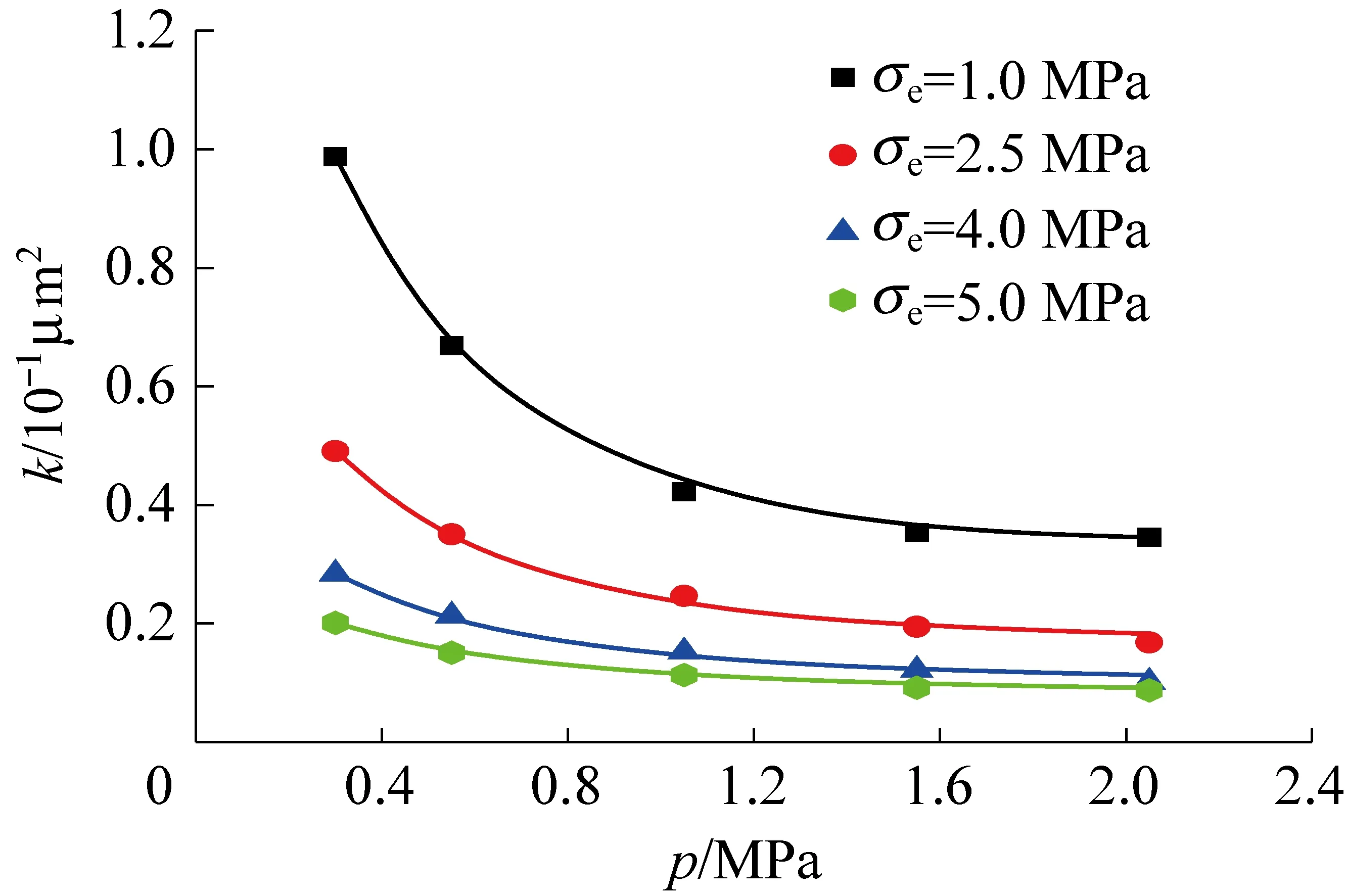
图3 不同有效应力下煤岩渗透率随气体压力的变化规律Fig.3 Coal permeability and gas pressure curves under different effective stresses

由图3可知，当利用新建模型计算该数据时，所得模型曲线与试验数据较为吻合。当有效应力恒定时，随气体压力升高，渗透率曲线呈先急剧下降后趋于平缓的趋势。同时，当气体压力恒定时，随有效应力升高，渗透率曲线逐渐降低，煤岩体积裂隙压缩性逐渐降低。随着有效应力的不断加载，煤岩逐渐被压密压实，可被压缩孔裂隙容积逐渐减小，瓦斯渗流通道变窄。此外，裂隙压缩性计算结果与GUO等[20]的研究为一个数量级，有效应力与裂隙压缩性系数呈负相关[21]。这是由于围压较低时，煤岩内部孔裂隙体积较大，有相对较大的可压缩空间。随着围压增加，煤岩孔裂隙可压缩体积减少。因此，煤岩体积裂隙压缩性系数随有效应力增大而减小。

4 结 论

1） 利用修正的Langmuir模型得到的模型曲线与试验值拟合度较好，在等温吸附试验的5个温度下，随着气体压力升高，煤岩瓦斯吸附量逐渐增大，但吸附速率呈下降趋势。在相同气体压力下，随着温度升高气体吸附量呈下降趋势。

2）构建考虑煤基质内部膨胀变形、温度及滑脱效应的煤岩渗透率模型。其计算值与试验值基本一致，反映了模型可靠性。在相同温度下，随着气体压力升高，煤岩渗透率先急剧下降后趋于平缓，有效内膨胀变形的不均匀分布系数β不断减小。

3） 由试验比较可知，当气体压力恒定时，随有效应力升高，渗透率曲线逐渐降低，煤岩体积裂隙压缩性系数呈下降趋势。模型计算得到的煤岩裂隙压缩系数与实验室所得值在同一数量级，可较好表征应力导致的煤岩裂隙体积变化，进一步表明煤岩孔裂隙结构和渗透特性的关联性。