基于奇异值分解的双算法织物缺陷检测
郑兆伦, 鲁玉军
(1.浙江理工大学 机械工程学院, 浙江 杭州 310018; 2.浙江理工大学龙港研究院, 浙江 温州 325802)
在纺织品生产过程中,织物表面缺陷严重影响了产品质量,因此织物缺陷检测是纺织行业中必不可少的一个重要环节。目前,大部分工厂仍在采用传统的人工检测方法[1],此方法虽然可以做到即时纠正一些错误,但是疲劳会导致不可避免的人为错误,并且通常难以检测到较为微小的织物瑕疵,成功率仅为60%~75%[2]。随着工业4.0的推广,视觉实时检测技术逐渐在织物疵点识别中应用。
目前,针对织物疵点检测主要分为以下4种方法:基于结构的方法、基于统计的方法、基于频谱的方法以及基于学习的方法[3]。基于结构的方法中,周文明等[4]提出视觉显著性算法,通过选取若干个与其最相似的图像块,计算与该图像块的差异值之和,并生成显著性图,最后对显著性图像进行阈值分割得到疵点。Dhivya等[5]在文中使用多尺度轮廓的方法提取边缘图,基于提取轮廓的特征由K最邻近方法(KNN)分类器提取和分类,所得结果较支持向量机(SVM)、受限制的玻尔兹曼机(RBM)和极限学习机(ELM)有更好的性能结果。基于统计的方法中,孙国栋等[6]提出一种基于灰度共生矩阵的反向投影算法,结合灰度共生矩阵纹理特征提取的特点和反向投影算法突出小物体的特性来获得疵点。Jing等[7]根据形态成分不同分离织物背景和前景,再重新组合获得去噪后的织物图像,以确保更精确织物瑕疵定位。何峰等[8]提出窗口跳步形态学算法,通过直方图均值化及设计形态学核做腐蚀运算,快速定位出疵点位置。Jiang等[9]提出了一种区域Sobel算法,通过Sobel算子进行区域划分,再对每个区域采用阈值分割确定疵点。基于频谱的方法中,顾菁等[10]提出基于小波变换与局部熵的织物疵点检测方法,先进行小波变换,然后分别计算正常织物和缺陷织物局部熵值,对比二者差值大小,设定差阈值识别并确定疵点。Li等[11]采用最优椭圆Gabor滤波器(EGF)代替Gabor滤波器,并采用随机漂移粒子群算法确定最优椭圆Gabor滤波器的最优参数,通过卷积的方式分离织物的背景和瑕疵。基于学习的方法中,Qin等[12]在现有的残差模块的基础上,增加一个新的卷积分支,根据网络层数动态调整感受野的大小,从而提出一种新的主干网络Hourglass-MRB,较原模型相比织物瑕疵识别率有较大的提升。Li[13]等利用多个带有多层感知器的微体系结构对网络进行优化,微体系结构的主要组成部分采用多尺度分析、滤波器因子分解、多位置池化和参数约简等技术构建,以提高紧凑模型中的检测精度,证实所提出的网络模型尺寸更小且检测精度更高。
以上针对纹理织物缺陷检测的算法,对缺陷与背景对比度较高,以及织物图量较大时有较好的检测效果,但对缺陷与背景对比度较低且织物图量有限时检测效果并不理想。针对上述问题,本文选用不同对比度的缺陷织物作为研究对象,利用织物背景和不同缺陷的差异性,采用基于奇异值分解的双算法织物缺陷检测技术,以期在织物缺陷与背景对比度较低时生成较优的检测效果图。
1 织物缺陷分类和算法检测流程
1.1 织物缺陷分类
本文根据织物缺陷特点从总体上把织物缺陷分为2类:洞形缺陷和线形缺陷,并通过织物缺陷处图像灰度方差值的大小来判定其属于何种缺陷。如图1(a)所示,该缺经织物图处的缺陷较窄,通过计算可得缺陷处的方差值较大,该缺陷被判为线形缺陷。当缺经织物图处的缺陷足够宽时,如图1(b)所示,其缺陷处的方差值则较小,此时可以判定该缺陷为洞形缺陷。

图1 缺经织物缺陷图片Fig.1 Picture of fabric with warp defect. (a) Linear defect; (b) Hole shape defect
综上所述,通过定量的方式来划分织物缺陷类型,可以很好的解决现有疵点的形态与尺寸变化范围较大而难以划分类别的难题。
1.2 基于奇异值分解的双算法流程
本文所用测试图像来自天池布匹缺陷数据库,图像像素大小为2 560×1 920。本文采用像素大小为256×256的窗口对采集到的图像进行分割,利用多线程操作提高图片处理速率,效果较好。示例图像如图2所示。

图2 示例图像Fig.2 Sample images. (a) Linear defect; (b) Hole shape defect
分割后的图像作为输入图像,其处理流程如图3所示。

图3 算法流程图Fig.3 Algorithm flow chart
第1步,对输入的灰度图像进行奇异值分解,计算出输入图像特征值和特征向量,选取若干项组成特征值图像;
第2步,用原图像与特征值图像做布尔差集运算模糊图像背景区域获得差值图;
第3步,采用均值滤波以及直方图均值化增强缺陷区域和背景区域之间的对比度;
第4步,通过设定方差阈值的方式初步确定织物缺陷的位置;
第5步,采用形态学开运算和膨胀运算消除噪声点干扰并扩大缺陷区域;
第6步,通过判断形态学处理之后缺陷面积区域是否大于阈值,是则证明此为洞形缺陷,确定其位置并令图像编号i′=i+1,否则进行水平和垂直方差计算并判断方差是否大于阈值,是则证明此为线形缺陷,确定缺陷位置并令图像编号i′=i+1,否则证明此为正常织物并令图像编号i′=i+1;
第7步,判断图像编号是否满足i>n,是则说明所有缺陷已经检测完毕,结束检测,否则选取图像编号i进行检测。
2 基于奇异值分解的双算法检测
2.1 奇异值分解及布尔差集运算
数字图像数据可以用矩阵来表示,因此可以采用矩阵理论和矩阵算法对数字图像进行分析和处理。在织物图片中存在大量相似纹理,由于需要检测的是面积较小的织物缺陷,因此这些纹理在图像处理中被视为冗余信息,在检测时应尽可能过滤以减小对检测结果的影响。奇异值分解可以针对任意形态的矩阵作特征值分解,本文采用此方法过滤冗余信息,奇异值分解如式(1)所示。
(1)
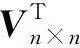
(2)
图4(a)为输入缺陷原图,分别为洞形缺陷和线形缺陷,对输入图像进行奇异值分解后,取前4项特征值和特征向量组成特征值图,效果如图4(b)所示,可以看出洞形缺陷的织物背景和织物缺陷能较好的分离,而线形缺陷分离效果较差,这是由于线形缺陷图片中织物缺陷面积较大,对特征值和特征向量产生了较大的影响,致使不能很好的分离缺陷和背景。通过把分离获得的特征值图和织物原图做布尔差集运算得到差值图,其效果如图4(c)所示。

注:1—洞形缺陷织物;2—线形缺陷织物。图4 原图与特征值图布尔差集运算Fig.4 Boolean difference set operation between original graph and eigenvalue graph. (a) Defects in original image; (b) Defect eigenvalue diagram; (c) Defect difference chart
2.2 均值滤波及直方图均值化
均值滤波是典型的线性滤波算法,其原理如式(3)所示。式中,g(x,y)是原像素;I(x,y)是相邻像素,即用模板中像素的平均值来代替原来像素值。差值图进行均值滤波的目的是消除缺陷位置的噪声点,使缺陷更加平滑,如图5(a)所示。

注:1—洞形缺陷织物;2—线形缺陷织物。图5 均值滤波及直方图均值化Fig.5 Mean filtering and histogram averaging. (a) Defect mean filtering; (b) Histogram averaging
(3)
直方图均衡化又称直方图平坦化,实质上是对图像进行非线性拉伸,重新分配图像像元值,使一定灰度范围内像元值的数量大致相等,让原来直方图中间的峰顶部分对比度得到增强,而两侧的谷底部分对比度降低,使输出图像的直方图变成一个较平的分段直方图,产生粗略分类的视觉效果。对均值滤波之后的图像进行直方图均值化使得织物背景区域的灰度方差值增大,而缺陷区域灰度方差值不变,效果如图5(b)所示。
由图5(b)可知,经过均值滤波和直方图均值化后,洞形缺陷织物中缺陷部分的灰度值方差与背景部分灰度值方差相比有较大的差距,而对于线形缺陷,其差值图效果较差,所以在均值滤波和直方图均值化后缺陷和背景没有被很好的划分,难以从处理后的图片中采用灰度值方差的方式确定缺陷位置。
2.3 方差阈值滤波
把经过均值滤波和直方图均值化的图像进行方差阈值滤波,可以初步确定缺陷位置,滤波原理如式(4)、(5)所示。
(4)
(5)
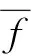
(6)
式中,lij为执行方差滤波的滤波核,其根据洞形缺陷的特点,设计为的十字形,如图6所示,此核的设计方式不仅能有效去除噪声点的干扰并且能较大限度地保留缺陷区域。
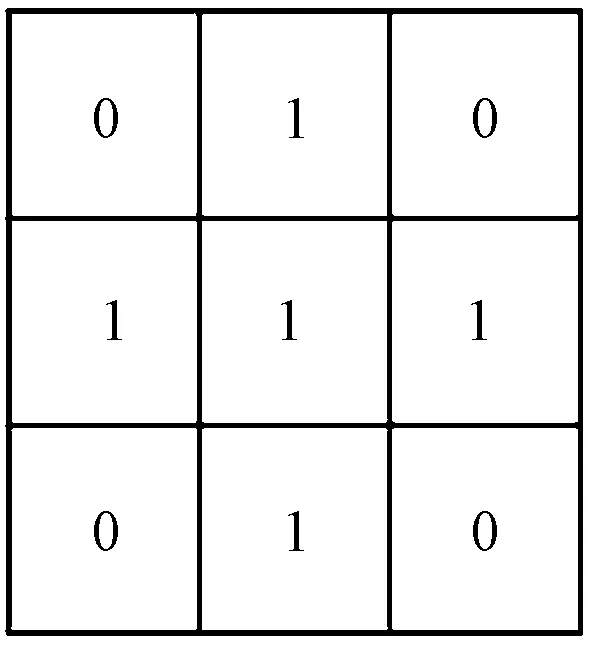
图6 方差阈值滤波核Fig.6 Variance threshold filter kernel
为提高方差滤波的鲁棒性,本文采用全图比例方差值来确定方差阈值,即在计算出整张图片像素方差值S2后,将该值乘以方差比例系数k,所得结果作为方差阈值。由于本文研究对象为具有纹理的织物,其背景区域方差值远大于缺陷区域方差值,即缺陷区域具有小方差值的特点,因此本文选用k=5%作为方差阈值滤波的比例系数。通过动态方差阈值滤波的方式,能够使缺陷的提取具有较好的适应性。
在设定参数后,首先将构造的滤波核遍历均值化图像后得到方差值图,再通过设置方差阈值的方式,去除灰度方差值较大的背景区域,最终保留下灰度方差值较小的缺陷区域,其效果如图7所示。

图7 方差阈值滤波Fig.7 Variance threshold filtering.(a) Linear defect;(b) Hole shape defects
2.4 形态学处理
形态学处理是利用数学形态学对分割后的织物图像进行背景修正,用于从图像中提取对表达和描绘区域形状有意义的图像分量,使后续的识别工作能够抓住目标对象最为本质的形状特征。基本运算有腐蚀、膨胀、开运算和闭运算,膨胀和腐蚀运算原理如图8所示。
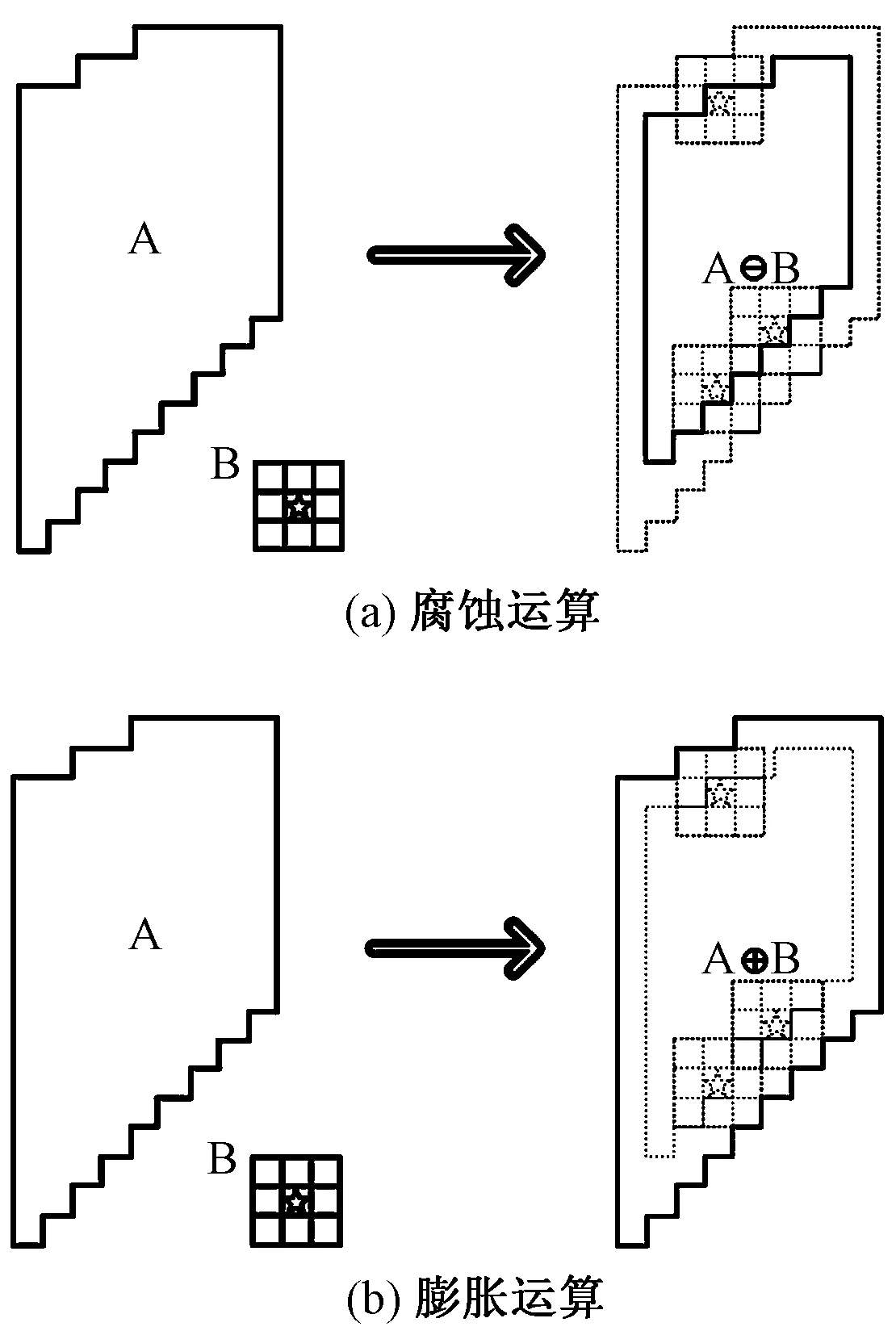
图8 膨胀和腐蚀运算原理图Fig.8 Schematic of expansion and corrosion operations. (a) Erosion operation; (b) Dilation operation
图中A为需要处理的图像,B为处理图像的核。膨胀为求局部最大值的操作,即核B与图形卷积,计算核B覆盖的区域的像素点的最大值,并把这个最大值赋值给参考点指定的像素,其作用是填充分割后疵点图像的边缘凹陷、内部沟槽等。腐蚀则是求局部最小值的操作,用于消融疵点图像的边界点,将小于结构元素的杂散疵点图像去掉,例如毛刺、孤立点凸角等。
开运算是先腐蚀后膨胀,其作用是去掉某些疵点图像边缘毛刺和孤立点、锐化角的同时也使其边缘平滑。闭运算是先膨胀后腐蚀,其作用填平疵点图像内部细小沟槽的同时也去掉了某些边缘杂散点[15]。
由图7可知洞形缺陷方差阈值滤波之后缺陷位置比较明显,但还存在噪声点的干扰,为此先采用形态学开运算去除较小的噪声点,再使用膨胀运算扩大缺陷面积,其效果如图9所示。

注:1—洞形缺陷织物;2—线形缺陷织物。图9 形态学处理Fig.9 Morphological processing. (a) Defect opening operation; (b) Defect expansion operation
2.5 面积阈值判别
由图9(b)可知经过形态学处理之后的图片噪声点干扰已经大幅度降低,洞形缺陷中存在着织物缺陷区域和少量噪声点,而对于线形缺陷而言,形态学处理之后仅含有少量的噪声点。根据此特征来判断洞形缺陷和线形缺陷类别,其步骤为:1)计算洞形缺陷和线形缺陷的最大连通域面积;2)判断最大连通域面积是否大于设定面积阈值,大于则判定为洞形缺陷,小于则判定为线形缺陷或正常织物。
2.5.1 洞形缺陷
当判定为洞形缺陷后需进一步确定缺陷位置和消除噪声点的干扰,本文提出的判定依据,如式(7)所示。
(7)
式中:DI为连通域I;SI为区域I的面积;SMAX为所有连通域中最大面积;k为面积比例系数。首先计算所有连通域面积DI,再依次判定连通域面积SI是否大于设定面积阈值SMAX×k,当SI大于SMAX×k时,判定其为缺陷,反之将此连通域面积判定为噪声点。由于洞形缺陷通常具有缺陷集中且面积大小相似的特点,因此本文点选取k=0.8作为洞形缺陷面积比例系数。除去噪声点的干扰后,在原图中标定二值图中所检测到的缺陷位置,以验证其准确性,效果如图10所示。

图10 洞形缺陷检测结果Fig.10 Detection results of hole defects. (a) Area threshold filtering; (b) Defect original drawing verification
2.5.2 线形缺陷及正常织物
当最大连通域面积小于设定阈值时,仅能够确定其为非洞形缺陷,既可能为线形缺陷,也可能为正常织物,由图9(b)可知上述算法不能很好地检测出线形缺陷,但在线形缺陷特征图中缺陷区域和背景区域有着明显差别,如图11所示。可以看出在特征值图11(b)中,织物背景区域处保留着纹理特征,而缺陷区域处存在着灰度值相似的线形,对于正常织物而言,因不存在缺陷,则整幅图像为较清晰的纹理特征。

注:1—纬纱缺陷;2—经纱缺陷;3—正常织物。图11 线形缺陷与正常织物特征值图对比Fig.11 Linear defects are compared with the eigenvalue diagrams of normal fabrics. (a) Original image; (b) Eigenvalue image
基于上述特征可以区分出正常织物和线形缺陷,其步骤为:1)分别计算特征值图像水平方向和垂直方向的方差值、方差均值及存储最小方差值;2)通过对比水平方向和垂直方向的最小方差值大小,较小的方差值方向为缺陷方向;3)确定方向后,用该方向的方差均值与最小方差值做差,通过设定差阈值的方式来判断是否为缺陷图像,如果差值大于阈值证明图像为线形缺陷,小于阈值则为正常织物图像;4)如果确定为线形缺陷,则选取最小方差值的k倍作为阈值来确定缺陷位置,判定方法如公式(8)所示。
(8)
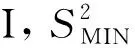

注:1—纬纱缺陷;2—经纱缺陷;3—正常织物。图12 线形缺陷和正常织物方差阈值滤波结果Fig.12 Linear defects and normal fabric variance threshold filtering results. (a) Eigenvalue image of fabric; (b) Image of variance threshold filtering
从图12可知,在经过方差阈值滤波之后,经、纬纱缺陷位置在方差阈值滤波图中被准确定位,而在正常织物图像中由于背景灰度方差值大于所设定的阈值,所以滤波图灰度值为0。
3 实验结果及分析
为验证本文算法的可行性,实验选用常见织物缺陷图像作为样本。其中包含破洞、毛洞、擦洞、缺经、缺纬、粗纬等十几种缺陷,共250幅。织物图像像素大小均为256×256。本文实验中所检测的算法是在Opencv环境下实现的,并在搭载 Intel Core i7处理器的Win10操作系统计算机上进行。
为对比算法效果,本文选用文献[1]所述的加权中值滤波K-means算法、文献[8]所述的窗口跳步形态学法进行对比,随机选取5种典型洞形缺陷和线形缺陷检测效果,3种织物缺陷检测算法准确率和平均耗时参数如表1所示。
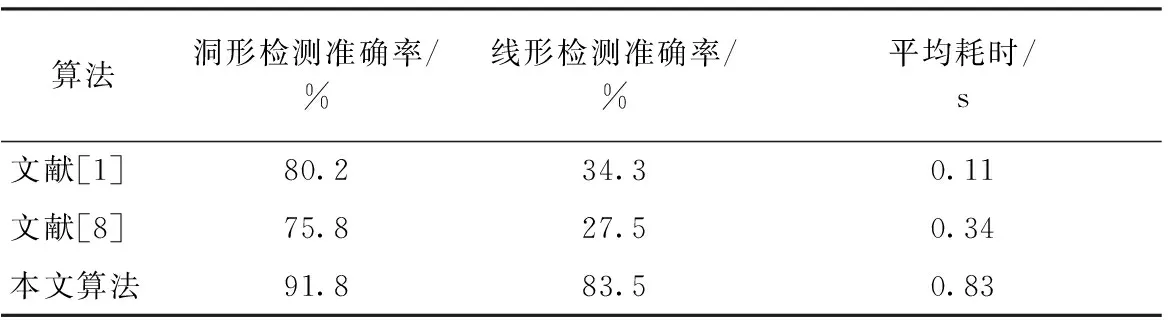
表1 3种织物缺陷算法比较Tab.1 Comparison of three fabric defect algorithms
图13、14分别示出洞形缺陷和线形缺陷的部分检测图。为了更好地表示出织物缺陷位置,本文将算法检测出的织物缺陷位置在输入织物原图上用方框标记突出显示,如图13(e)和图14(e)所示。

注:1~5分别为5种典型洞形缺陷织物。图13 洞形缺陷对比图Fig.13 Comparison diagram of hole defects. (a) Original image; (b) Method of reference [1]; (c) Method of reference[8]; (d) Method of this paper; (e) Detection results of this paper

注:1~5分别为5种典型线形缺陷织物。图14 线形缺陷对比图Fig.14 Linear defect comparison diagram. (a) Original image; (b) Method of reference [1]; (c) Method of reference[8]; (d) Method of this paper; (e) Detection results of this paper
从表1可知,文献[1]和文献[8]在洞形缺陷检测上准确率分别为80.2%和75.8%,而在线形缺陷检测上仅有34.3%和27.5%。文献[1]首先通过加权中值滤波模糊织物背景的同时使得织物缺陷处灰度值相等,然后通过K-means算法得出分割阈值,最后通过阈值分割背景和疵点,从图13(b)所展示的检测结果可知此算法对于洞形缺陷分割效果较好,尤其是疵点和背景灰度值相差较大的情况下,但对于织物缺陷处灰度值和背景灰度值相近,此算法则很难获得一个较好的阈值来划分背景和疵点,这一点对于对比度不高且缺陷分散的线形缺陷更加明显,如图14(b)所示,只有当线形缺陷和背景灰度值相差较大时才有较好的分割效果。文献[8]则是通过迭代法获取二值化阈值,然后通过形态学处理的方式来模糊背景并突出织物缺陷区域,此算法在洞形缺陷有较好的分割能力,但同样难以检测出背景和疵点对比度不高的缺陷。在线形缺陷中,由于缺陷狭长且灰度值与背景相似,此算法所设计的十字形态学核在进行卷积运算时会把缺陷同背景一起腐蚀,如图14(c)第1组所示,缺陷位置因为和背景灰度值相似导致最后获得的检测图未包含织物缺陷。
本文针对洞形缺陷特征图及线形缺陷特征值图特性,设计出双算法进行检测,在检测洞形缺陷和线形缺陷中的准确率分别为91.8%和83.5%,平均耗时为0.83 s,相比于其他2种方法,本算法耗时稍高于其他2种算法,此问题可以通过对算法进行优化或者提升硬件条件等方法来减少检测时间。但在疵点检测准确率上,本文算法明显高于其它两种算法,证明此算法能有效地检测出高对比度、低对比度、线形及洞形缺陷,能有效地去除噪声点的干扰,正确地标定出织物缺陷区域,检测效果最好。
4 结 论
本文针对常见的洞形缺陷和线形缺陷图像特征进行研究,提出了基于奇异值分解的双算法织物检测的方法。利用奇异值分解和布尔差集运算模糊织物图像背景区域并凸显织物缺陷区域;再通过均值滤波、直方图均值化、方差阈值滤波及形态学运算消除图像噪声点干扰初步获得缺陷区域;最后用面积阈值和水平、垂直方向方差的方式区分线形缺陷、洞形缺陷及正常织物和确定缺陷位置。将本文方法得到的疵点检测效果与其他检测方法生成的疵点检测效果图进行比较,本文方法不仅能够很好地检测洞形缺陷,而且在线形缺陷上也有很好的表现,解决了不能有效地同时检测洞形缺陷和线形缺陷的问题。实验证明了本文算法的有效性和可靠性。

