船舶阀门电动静液作动器混合灵敏度鲁棒控制器设计
杜 伟, 汪成文,2, 赵赞魁, 赵俊奇
(1.太原理工大学机械与运载工程学院, 山西太原 030024;2.太原理工大学新型传感器与智能控制教育部山西省重点实验室, 山西太原 030024)
引言
船舶阀门遥控系统是应用于控制与监测船舶压载水系统、舱底水系统、消防系统等系统中的管路阀门,以实现对船舶控制的自动化、智能化。目前,根据遥控阀门作动器的作动类型,可以分为气动式作动器、电动式作动器、液压式作动器与电液式作动器[1]。相比传统液压式,电液式作为一种新型驱动装置,以电缆取代液压管路,极大提高系统响应速度、设备可靠性,同时降低系统设备维护成本。电液式阀门遥控系统的核心元件为电液一体式阀门执行机构,即电动静液作动器。该作动器是一种集成一体化容积控制直接驱动的电液位置伺服系统,通过将传统液压作动系统中液压源与作动执行装置高度集成于一体,实现作动器的小型化、一体化、模块化。同时,电动静液作动系统兼具传统液压作动系统与机电作动系统的优势,即高转矩与高功重比、高可靠性[2-4]。
由于电动静液作动器所具备的特点及优势,其广泛应用于伺服驱动重载工况,一些学者开展了对于电动静液作动器相关应用的研究。付永领等[5]针对电动静液作动器系统存在死区现象以及系统中参数不确定问题,提出一种新型自适应变阻尼滑模控制方法,仿真结果表明,该控制策略有效提高系统位置跟踪性能。王岩等[6]针对电动静液作动器散热问题,提出了一种新的热力学建模方法,并建立三维热力学模型验证所提出方法的正确性。文献[7]针对电动静液作动器应用于飞机舵机存在电机发热的问题提出了一种新型电动静液作动器,该作动器通过液压能量回收单元减少电机发热。
然而,现有针对船舶阀门遥控系统领域电动静液作动器应用研究较少。对于船舶阀门遥控系统电动静液作动器,其泵转速相较于飞机舵机电动静液作动器更低,系统阻力的影响更为显著,并且船舶阀门启闭负载特性可通过计算获取。同时,电动静液作动器系统在运行时油液弹性模量受含气量、温度和压力的影响变化范围较大,并且无法精确建模,影响系统动态响应,使得系统存在模型不确定性。而H∞鲁棒控制理论是处理系统不确定性的有效手段。
本研究针对电动静液作动器应用于船舶阀门遥控系统使用背景,建立系统数学模型,通过计算中线型蝶阀不同开度下启闭总阻力矩,拟合为连续曲线作为系统负载特性,模拟中线型蝶阀真实启闭阻力特性,并采用H∞混合灵敏度控制方法,设计鲁棒控制器,最后进行联合仿真,通过与PID控制对比验证了所提控制策略的优越性。
1 电动静液作动器系统描述
电动静液作动器系统原理图如图1所示,系统的主要元件包括:直流无刷电机、双向定量泵、蓄能器、液控单向阀、溢流阀以及齿轮齿条液压缸。系统的基本工作原理为通过反馈调节直流无刷电机的转速与旋转方向,从而实现控制双向定量泵压力油的流量大小和输出方向,并通过齿轮齿条液压缸将活塞的直线运动转化为蝶阀的旋转运动,进而实现蝶阀的开闭动作。其中,蓄能器的作用是补充油液与防止产生气穴;溢流阀的作用是防止液压缸两腔压力过高。

图1 电动静液作动器系统原理图Fig.1 Schematic diagram of electro-hydrostatic actuator system
2 系统数学模型
2.1 直流无刷电机模型
电动机电枢回路电压平衡方程、动力学方程、感应电动势表达式与电磁转矩表达式可以得到电机闭环回路传递函数:
(1)
式中,uc—— 电枢电压
R—— 电枢电阻
L—— 电枢电感
i—— 电枢电流
E—— 电枢反电势
E的表达式为:
E=Ceω
(2)
式中,Ce—— 反电动势系数
电机电磁转矩为:
Te=Cmi
(3)
式中,Cm—— 转矩系数
电动机输出轴转矩平衡方程:
(4)
式中,J—— 转动惯量
Bm—— 电机阻尼系数
ω—— 电动机转速
联立式(1)~式(4),考虑电枢电感L值较小,忽略其影响,将电动机输出转速ω与电枢电压uc的二阶微分方程化简为一阶微分方程:
(5)
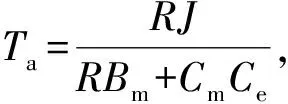
2.2 泵和液压缸模型
泵的流量连续性方程[8]:
Qa=Dpωp-φim(pa-pb)+φempa
(6)
Qb=Dpωp-φim(pa-pb)-φempb
(7)

(8)
式中,Qa,Qb—— 泵两端口流量
Dp—— 泵排量
ωp—— 泵转速
φim—— 泵内泄漏系数
φem—— 泵外泄漏系数
pa,pb—— 泵两端口压力
QL—— 负载流量
液压缸流量方程:
(9)
(10)
(11)
式中,Q1,Q2—— 液压缸两腔流量
A—— 活塞作用面积
x—— 活塞位移
V0—— 液压缸两腔容积初始容积
Vt—— 液压缸两腔总容积
cim—— 液压缸内泄漏系数
cem—— 液压缸外泄漏系数
p1,p2—— 液压缸两腔压力
βe—— 油液体积弹性模量
液压缸输出力与负载方程:
(12)
式中,M—— 活塞及负载折算在活塞上的总质量
B—— 黏性阻尼系数
FL—— 外界干扰力
联立式(6)、式(9)、式(12)整理得到活塞位移对于泵转速的传递函数:

(13)
式中,c—— 总泄漏系数,
系统整体结构图如图2所示,图中K为控制器。结合直流无刷电机模型,得到电动静液作动器系统传递函数:
(14)
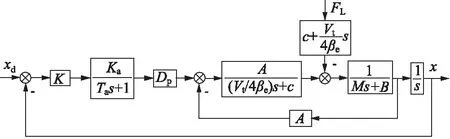
图2 系统整体结构图Fig.2 Structure of system
3 系统的外部干扰与参数摄动
电动静液作动器工作时会受到来自外部的干扰,本研究以中线型蝶阀垂直安装为例,计算蝶阀在启闭过程中蝶阀不同开度下的阻力矩,并拟合为连续曲线作为系统的外部干扰。垂直安装中线型蝶阀的总启闭力矩[9-10]为:
T=Tm+Tz+Td+Tt
(15)
式中,Tm—— 密封面摩擦力矩
Tz—— 轴套摩擦力矩
Td—— 动水力矩
Tt—— 填料摩擦力矩
Tj—— 静水力矩
密封面摩擦力矩:
Tm=4qbbmμR2
(16)
(17)
式中,qb—— 密封比压
bm—— 接触面宽度
μ—— 密封面摩擦系数
R—— 蝶阀密封半径
p—— 工作压力
轴套摩擦力矩:
Tz=0.5Fμzd
(18)
式中,F—— 作用在阀杆轴承上的载荷
μz—— 轴套摩擦系数
d—— 阀杆直径
当蝶阀处于全闭时:
F=0.25πD2p
(19)
式中,D—— 蝶板直径
当蝶阀处于启闭过程中时:
(20)
H=100(PN+Δp)
(21)
(22)
式中,Fd—— 动水作用力
λα—— 蝶板开度为α时的动水力系数
ρ—— 液体密度
g—— 重力加速度
H—— 计算升压在内的最大静水压头
ξα—— 蝶板开度为α时的流阻系数
ξ0—— 蝶板全开时的流阻系数
v0—— 蝶板全开时液体流速
PN—— 蝶阀公称压力
Δp—— 由于蝶阀快速关闭产生的水击升压值
Q—— 体积流量
A—— 阀座通道截面积
t—— 蝶阀启闭时间
动水力矩:
(23)
式中,μα—— 蝶板开度α时的动水力矩系数
填料摩擦力矩:
Tt=0.5Qtd
(24)
Qt=πdhtμtp
(25)
式中,Qt—— 摩擦力
ht—— 填料高度
μt—— 填料摩擦系数
中线型蝶阀相关参数如表1所示。
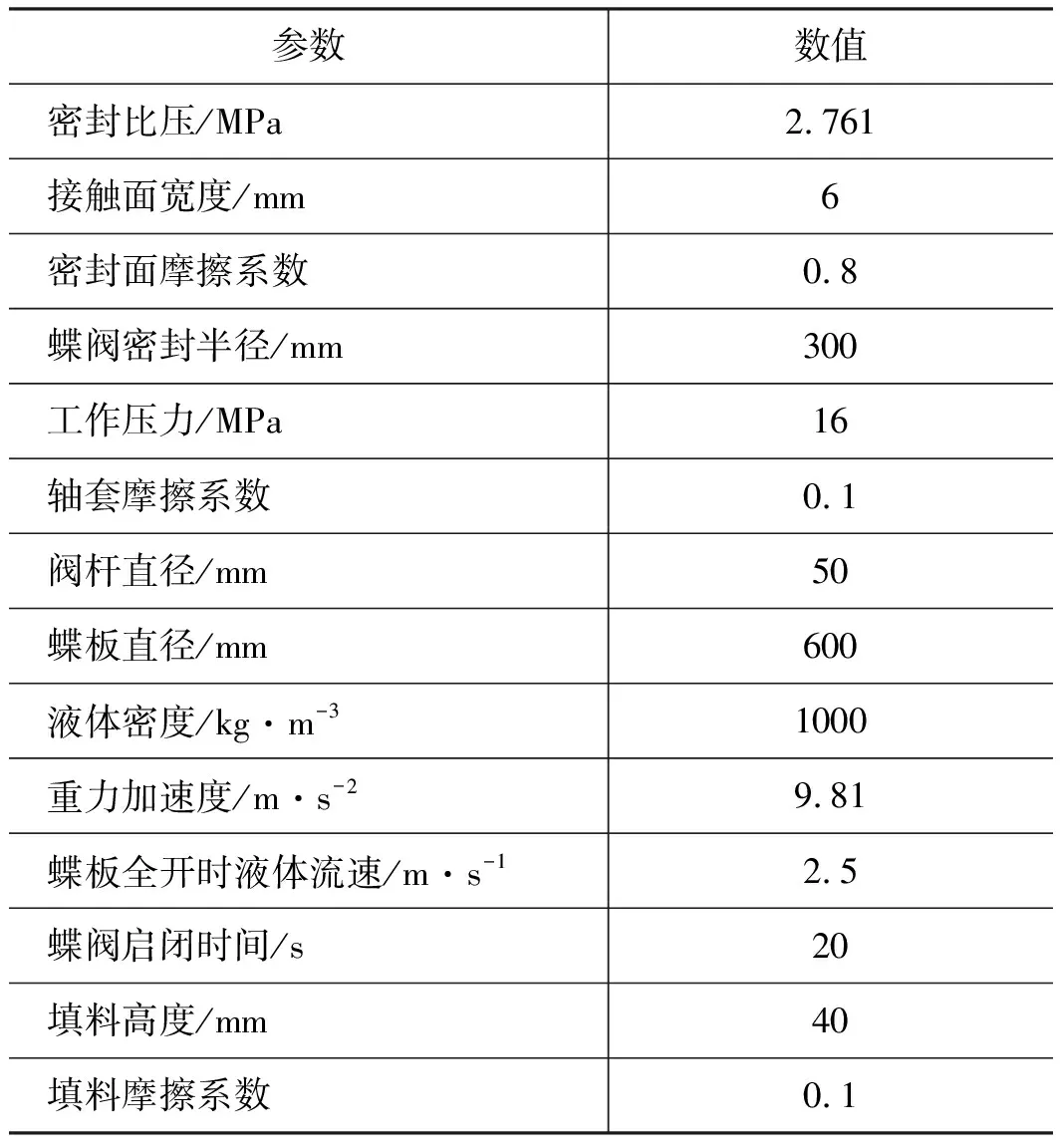
表1 中线型蝶阀相关参数Tab.1 Relevant parameters of centerline butterfly valve
通过在蝶阀不同角度下计算各个阻力矩,并将各数据点拟合为连续曲线,拟合规则采用多项式拟合,拟合函数表达式为:
y=426.052x-277.225x2+43.633x3-3.267x4+
0.132x5-0.003x6+3.083×10-5x7-
1.187×10-7x8+2148.85
(26)
根据拟合函数得到蝶阀启闭阻力力矩如图3所示。该拟合曲线将在联合仿真中作为液压缸活塞外部干扰力,真实模拟中线型蝶阀启闭总阻力力矩特性。
由图3可知,中线型蝶阀启闭过程中阻力力矩波动较大。阻力峰值出现在蝶阀开启约15°时,随开启角度增大,阻力力矩迅速减小;在关闭蝶阀的过程中,由于动水力矩的作用,总阻力力矩出现负值,之后阻力力矩逐渐增大至正值。
由式(14)可知,对于已经选定规格并投入生产使用的船舶阀门电静液作动器,系统中与作动器设计的相关参数,如泵排量等参数不会出现大范围波动。而电动静液作动器结构紧凑导致作动器散热性较差[11],以及船舶航行所引起的环境温度变化,使油液弹性模量受含气量、环境温度以及系统压力影响变化较为显著[12],同时弹性模量对于系统固有频率与阻尼比存在重要影响,因此本研究以油液弹性模量作为系统参数的不确定性。

图3 中线型蝶阀启闭总阻力力矩拟合曲线Fig.3 Fitting curve of total resistance moment of opening and closing of midline butterfly valve
由于中线型蝶阀启闭总阻力矩的复杂性,以及系统所存在的参数摄动。考虑到鲁棒控制对于系统模型不确定性与外部干扰不确定性有良好的鲁棒性[13-16],因此本研究采用鲁棒控制器作为系统位置伺服控制器。
4 H∞混合灵敏度控制器设计
对于系统参数油液弹性模量的摄动,本研究采用乘性不确定性进行描述[17]:
(27)

P(s) —— 标称系统传递函数
Δ(s) —— 未知的摄动函数
WT(s) —— 补灵敏度加权函数
本研究中标称系统油液弹性模量设定686 MPa,即为参数摄动上界,参数摄动下界设定为1 MPa,系统不确定性估计可由下式表示[18]:
(28)
选取补灵敏度加权函数为:
(29)
补灵敏度加权函数与系统乘性不确定性关系如图4所示。
由图4可知,补灵敏度加权函数满足|WT(jω)|≥σmaxE(jω),同时尽可能贴近参数摄动上界以减小控制器的保守性。选取灵敏度加权函数:
(30)

图4 补灵敏度加权函数与参数摄动Fig.4 Complementary sensitivity weighting function and parameter perturbation
选取的加权函数与系统灵敏度函数、补灵敏度函数关系如图5所示。由图5可知,加权函数的选取满足:
(31)
(32)


图5 加权函数与灵敏度函数、补灵敏度函数Fig.5 Weighting function and sensitivity function, complementary sensitivity function
根据所选加权函数与被控对象数学模型,利用MATLAB鲁棒控制工具箱求得控制器。
K(s)=2.1965e13s(s+55.56)(s+29.29)/
[(s+1.316e4)(s+0.000196)×
(s2+762.6s+2.796e5)]
(33)
鲁棒控制器性能指标γ=0.667,即闭环系统在所有频率内的最大奇异值小于1,表明系统闭环传递函数的无穷范数满足要求。

图6 联合仿真模型Fig.6 Co-simulation model
5 联合仿真
利用MATLAB/Simulink与AMESim仿真平台,搭建船舶阀门电动静液作动系统联合仿真模型。其中,在AMESim软件中搭建液压系统模型,在MATLAB/Simulink软件中建立H∞混合灵敏度控制器模型[19-20]。联合仿真模型如图6所示,仿真参数如表2所示。
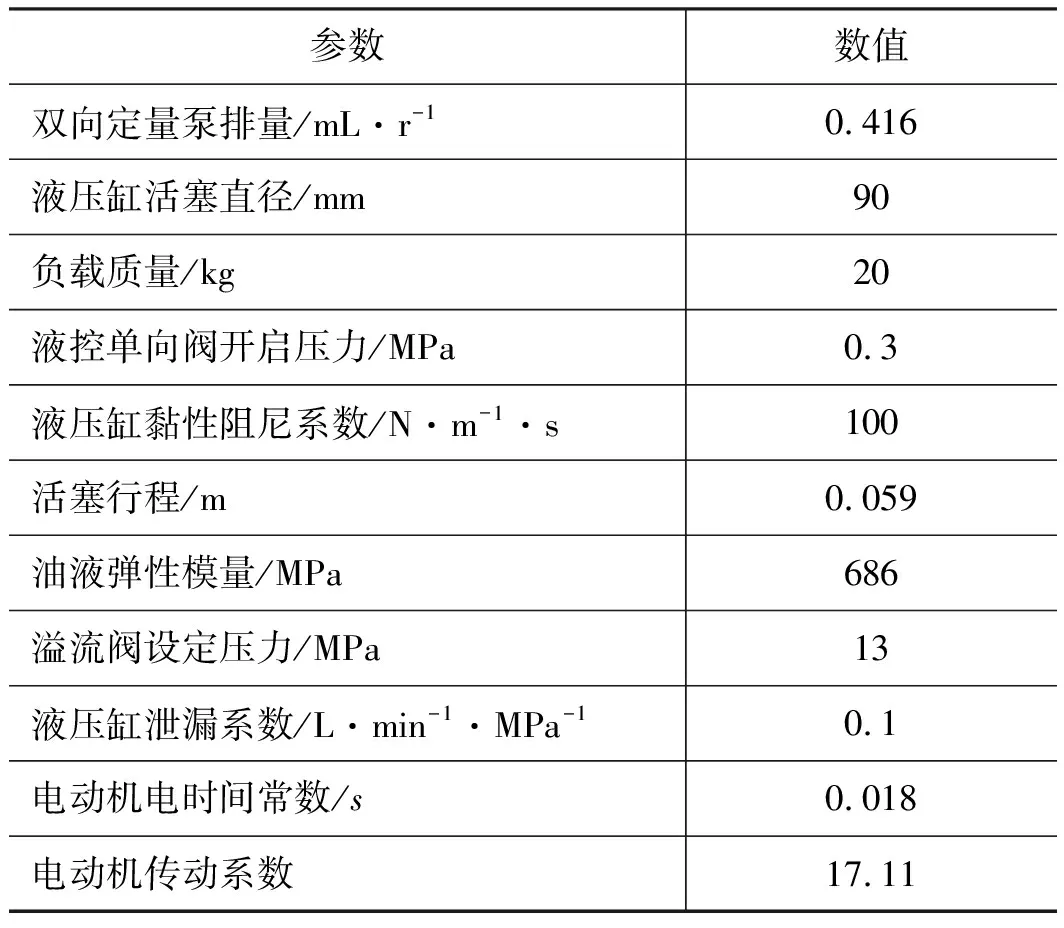
表2 电动静液作动系统仿真参数Tab.2 Electro-hydrostatic actuator system simulation parameters
通过与PID控制器进行对比,验证所设计控制器的优越性。经过多次仿真实验,选取PID控制器参数为Kp=1×106,Ki=10。
联合仿真模拟船舶阀门开启/关闭过程,对应前文所述的干扰情况,分别从以下3种情况将鲁棒控制器与PID控制器进行对比:无干扰情况下跟踪幅值为0.059 m、周期为40 s的三角波信号,模拟蝶阀空载开启/关闭过程;将蝶阀开启/关闭阻力矩施加于执行器末端,跟踪幅值为0.059 m、周期为40 s的三角波信号,目的在于模拟真实负载下蝶阀阀门开启/关闭过程;系统油液弹性模量参数摄动情况下,跟踪阶跃信号,目的在于测试当油液弹性模量发生变动对系统动态响应的影响,以及系统针对参数变化的鲁棒性。
(1) 无干扰情况下,系统跟踪幅值为0.059 m、周期为40 s的三角波信号。由图7可以看出,PID控制器跟踪误差为1.54×10-4m,鲁棒控制器跟踪误差为1.38×10-4m,相比于PID控制器跟踪误差减少了10.4%。

图7 无干扰下跟踪三角波信号Fig.7 Tracking triangular wave signals without interference
(2) 将蝶阀开启/关闭阻力矩施加于作动器末端,系统跟踪幅值为0.059 m、周期为40 s的三角波信号。由图8可以看到,当阻力矩施加于执行器末端,由于系统负载在蝶阀开启前5 s内阻力矩较大,液压缸出现了短暂的死区现象,随着阻力矩的降低同时液压缸内压力升高,跟踪误差逐渐减小。由图8可以看出,PID控制器最大跟踪误差为2.85×10-3m,鲁棒控制器最大跟踪误差为2.73×10-3m,相比PID控制器减小了4.2%。5 s后,鲁棒控制器与PID控制器跟踪误差均恢复至加入干扰前的水平。综上可得,当蝶阀阻力矩施加于作动器末端后,鲁棒控制器相比PID控制器跟踪误差更小,对外部干扰的鲁棒性更强。

图8 干扰下跟踪三角波信号Fig.8 Tracking triangle wave signal under interference
(3) 系统油液弹性模量参数由686 MPa减小至1 MPa,控制器参数不变的情况下跟踪阶跃信号,仿真结果如图9所示。从图9a可以看到,在参数为变动前,PID控制器的调节时间为0.23 s,鲁棒控制器的调节时间为0.35 s;当油液弹性模量减小,系统固有频率降低,阻尼比降低。由图9b可以看到,PID控制器发生明显的超调与振荡,最大跟踪误差为1.2×10-4m,超调量为12%,调节时间为2.95 s;而鲁棒控制器最大跟踪误差为3.5×10-5m,超调量为3.5%,调节时间为2.18 s,最大跟踪误差相比PID控制减小了70.8%。由此可以看到,鲁棒控制器在系统参数发生变动后,系统鲁棒性比PID控制器更强。

图9 参数摄动下跟踪阶跃信号Fig.9 Tracking step signal under parameter perturbation
6 结论
本研究以电动静液作动器系统为研究对象,根据船舶阀门应用工况,综合考虑系统外部干扰力以及参数摄动情况,将混合灵敏度鲁棒控制算法应用于电动静液作动器系统中,提高了该系统的位置跟踪性能。
(1) 计算中线型蝶阀不同开度下启闭总阻力矩,拟合为连续曲线作为系统负载特性,提高仿真真实度。
(2) 针对系统中油液弹性模量参数摄动的情况,设计基于H∞混合灵敏度控制器。通过与PID控制器的仿真对比,结果表明所设计的控制器的位置跟踪误差更小,对系统收到外部干扰以及系统参数发生摄动时的鲁棒性更强,拥有更好的控制效果。

