列车自动驾驶准点目标速度在线计算方法
何珊
(西南交通大学信息科学与技术学院,四川 成都 610031)
现行的ATO控车系统大部分采用计算目标速度曲线的方式对列车速度进行调控,因此对目标速度曲线的计算优化和优化列车速度跟踪器成为了学者研究的热点。如安志强[1]采用粒子群算法对ATO目标速度曲线进行了多目标优化,并采用模糊自适应控制理论设计了ATO速度控制器,其控制性能优于PID控制器;张京等[2]针对列车自动驾驶的精确停车、准时性、舒适性及能耗等指标提出了一种用遗传算法改进的新型粒子群算法(GAPSO),该算法对ATO指标都进行了一定程度的优化;王彪[3]提出一种基于非线性自抗扰控制器的列车速度跟踪控制系统,以解决列车非线性、大时滞、多干扰、难建模、强耦合的速度跟踪控制问题;李相儒等[4]采用最优预见算法设计ATO的速度控制器,一定程度上降低了列车的能耗。但是上述优化算法都是针对ATO控车指标(如准点、节能、舒适等)进行优化,但是无法达到减小车载计算机计算量的目的,并且增大了系统的复杂性。为解决该问题,本文提出一种可在线周期计算列车准点目标速度的算法,以提高ATO控车的实时性和精确性,并满足列车准点指标。
1 准点目标速度计算模型
基于运营计划的目标速度也称为准点目标速度,列车准点指列车从本站出发,根据运营计划规定的运行时间准时到达下一站,准点目标速度则是在顶棚速度区列车应该达到的速度。本模型将ATO控车过程划分为3个阶段:升速阶段、恒速阶段和降速阶段,如图1所示。

图1 ATO控车过程
设此时列车位于图中P车,车速为V车,从V车升速为顶棚速度的距离为Sup,从顶棚速度降速为0的降速距离为Sdown,按照顶棚速度行驶的距离为Sconstant,则列车距离站B的剩余距离Sleft可以表示为:

设Sup、Sdown、Sconstant对应的列车时间为Tup、Tdown、Tconstant,则根据运营计划列车剩余到站时间表示为:

因此模型准点目标速度表示为:

即只要计算出Sup、Sdown、Tup、Tdown即可求解本模型的准点目标速度。由于车载ATO的速度自动调整模块[5-7]会根据计算得到的目标速度对列车速度进行调整,若不考虑前期升速阶段的走行距离和时间得到的目标速度可能会偏大或偏小,但是这些误差可以在自动调速阶段进行调整,但降速区段必须预先计算出列车当前速度制动停车所需要的制动距离以保证行车安全,因此公式(1)可简化为:

下面介绍降速距离Sdown和降速时间Tdown的计算模型。
2 降速距离计算模型
2.1 模型描述
由于车载ATO进行命令传输存在时延,因此将列车制动过程细分为3个阶段,如图2所示。

图2 降速距离计算模型
牵引卸载阶段。车载ATO已接收到制动命令,但列车控制单元还未响应,响应时间包括列车定位延时tlocation、牵引切除命令传输时间tcmdTransfer、牵引切除命令建立时间tcreateCutTraction、牵引切除时间tcutTractionDelay,本阶段延时计算如下:

惰行阶段。列车牵引完全切除,但制动还未建立,延时包括制动命令响应延时tcreateBrakeCmd、制动命令建立延时tcreateBrake,本阶段延时计算如下:

制动力完全施加阶段。列车制动已完全建立,列车开始制动至列车停车。
2.2 模型计算
考虑制动延时,以速度V0降速为速度V1的制动距离Sdown计算模型如下。
步骤1,先计算列车在牵引卸载阶段走行的距离。设本阶段以最不利情况加速,加速度为atraction;本阶段结束后列车速度为Vtraction,本阶段列车运行距离为ΔStraction:

步骤2,以Vtraction进入惰行延时阶段。本阶段考虑最不利情况加速,设加速度为最不利下坡道加速度为agradient,Vcoast为惰行结束后列车速度,ΔScoast为本阶段运行距离:
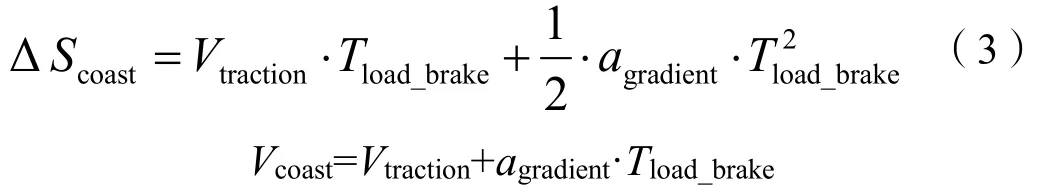
步骤3,计算制动阶段距离(即图2中③段)。查询车辆制动特性表,确定当前速度Vcoast对应的制动减速度abrake,由于制动阶段所处位置未知,因此无法确定坡道加速度,根据公式V2-V02= 2aS粗略计算不考虑坡道加速度的制动距离:

步骤4,校正制动阶段减速度abrake。上述制动阶段由于X0位置未知,无法考虑坡道附加阻力的影响,计算的制动距离存在较大误差,因此现依据公式(2)—(4)估计X0位置,从而可确定列车位置:
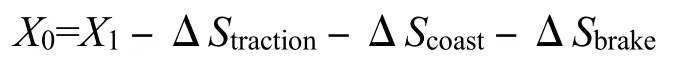
列车位置确定后采用多质点模型[8]对计算列车所受平均坡道加速度agradient_ave。列车横跨多坡道示意图如图3所示。

图3 列车横跨多坡道示意图
设每段坡道上列车长度为li,每段坡道角度为θi,则列车所跨坡道高度变化H和平均坡道加速度agradient_ave可表示为:

因此abrake可以校正为:

步骤5,使用校正后的制动减速度brakea′对制动距离ΔSbrake进行校正。设校正后的制动距离为Sdown,用能量守恒分析X0点到X1点的能量变化,如公式(5)所示:

式(5)中:E1为X1点动能;E0为X0点动能;Wtraction为牵引卸载阶段做的功;Wcoast为惰行阶段做的功;Wbrake为制动阶段做的功。
每一部分的能量计算联立可得方程组:

将公式(3)(4)代入方程组(6)可化简得到校正后的制动距离Sdown:

步骤6,由于ATO控车采用的是平均制动减速度,因此根据制动距离Sdown计算其对应的平均制动减速度aaverage:

从而可计算制动时间为:
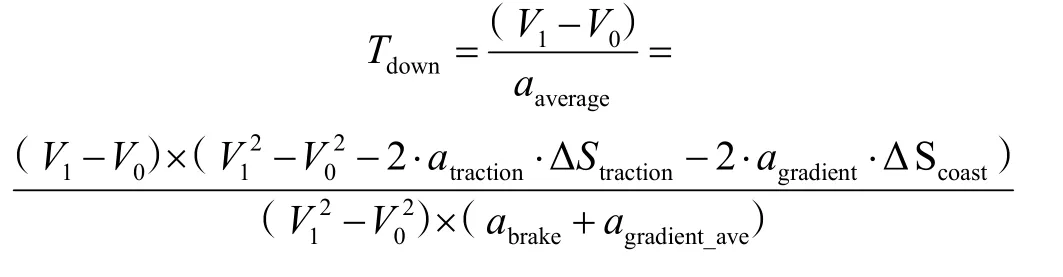
上述模型可完成速度V0降为速度V1的制动距离计算。当降速阶段存在多段限速区时,两两相邻的限速区之间的制动距离和制动时间按照上述6个步骤可依次计算,最后将多段制动距离(制动时间)进行累加,即可得到降速区段的总距离和总时间。若存在限速区长度小于制动距离的情况(如图4限速区k),按照上述步骤计算的制动距离会发生越过2个或以上限速区的情况,如图4所示。
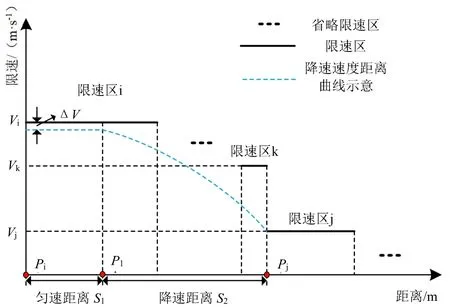
图4 限速区长度小于制动距离示意图
设限速区j的起点坐标为Pj,先根据上述6步计算限速区i制动到限速区j的制动距离S2,由此可计算降速距离的起点坐标P1:

设限速区i起点坐标为Pi,则Pi到P1间的距离即为匀速行驶距离S1:

限速区i中匀速行驶时间T1为:
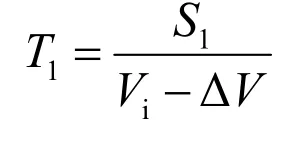
根据上述模型即可计算每一周期列车速度制动停车所需的制动距离和制动时间,再按照图1模型周期计算准点目标速度,并与列车实际速度进行比较,当实际速度与准点目标速度有偏差时,列车速度自动调整模块会根据偏差向列车牵引/制动系统输出相应控车指令,使列车速度逼近目标速度,实现准点控车功能。
3 仿真结果验证
为验证上述方法的正确性,借助北京和利时系统工程有限公司的列车仿真实验室对在线准点目标速度计算方法进行仿真。选取北京地铁亦庄线线路宋家庄站到肖村站作为仿真对象进行仿真验证,两站间无限速区,列车站间运行标准时间为3 min,站间线路长度为2 631 m。采用地铁B型列车为对象进行研究,其运行最高速度为120 km/h,车长114 m,车质量131.52 t。仿真数据如表1所示。

表1 站间无限速下不同计划运行时间准点功能仿真
根据表1分析可知,针对站间无限速的简单线路,本文提出的目标速度计算方法可以保证列车准时到达站点。
4 结束语
计算机仿真结果证明,将能量守恒原理运用到ATO目标速度的计算,所得到的目标速度不仅可以保证列车的准点指标,并且与现有计算目标速度曲线的方式相比,每个计算周期仅计算单个目标速度的方式极大地减小了车载计算机的计算量,对列车自动驾驶系统目标速度的计算具有创新意义。

