铆接接头剪切面残余应力对抗剪强度的影响分析

吴 浪， 侯红玲， 郝海凌, 张 炜, 王 凯, 黄 涛

(陕西理工大学 机械工程学院， 陕西 汉中 723000)

飞机装配是现代飞机制造的重要组成环节，各部件之间的装配不可避免地会采用各种连接技术，如铆接、螺栓连接、焊接、粘接等[1-4]。其中，铆接仍然是主要的连接方法，特别是对于金属构件，因为铆接具有工艺简单、密封性好、强度可靠等特点[5]。然而，铆接件在承受比较大的极限载荷时，以铆钉发生剪切失效居多，铆接过程中的孔径配合尺寸会导致干涉配合尺寸的变化，进而影响铆接搭接接头的内部力学性能。为了保证飞机的安全性能，研究铆接搭接接头的机械响应是必要的[6]。

国内外学者对铆接的研究主要集中在铆接接头附近的变形以及应力分布对其铆接质量的影响。张青等[7]通过建立C/SiC铆接接头有限元模型，研究了铆接孔周围应力分布和剪切破坏形式，结果表明当铆钉轴向在受到大于铆钉材料的剪切强度时，铆钉发生剪切破坏。Li等[8]和Zeng等[9]通过对不同孔径和挤压力的组合进行试验和仿真模拟，对铆接过程中干涉量分布和材料流动特性进行分析，结果表明，内板孔径的膨胀量大于外板，随着孔径和挤压力的增大，更多的铆钉材料流入孔内导致干涉量增大，且随着孔径增大剪切载荷逐渐增大。张开富等[10]建立了铆钉弹性变形、塑性变形和回弹性的数学和力学模型，通过实例的计算证明了有限元的正确性。王安强等[11]通过试验对比分析了普通铆接试验件和过盈量1%铆接试验件的疲劳寿命，结果表明过盈量为1%的铆接紧固件可提高紧固孔的疲劳寿命15%左右。李奕寰等[12]通过试验和数值模拟对不同倾角铆模铆接的铆钉镦头、干涉量和残余压应力进行了研究分析。结果表明，铆模倾角对干涉量有较大影响，倾角越小，干涉量越大；采用66°铆模倾角可以实现较理想的干涉配合使铆接接头疲劳寿命最长。杨宝惠等[13]通过试验对TC4钛合金构件电磁铆接极限间隙量进行了研究，结果表明，随着钉孔间隙量的增加，墩头直径和高度均呈现出近线性递减，但试件剪切强度和失效强度明显提高；宋承裕等[14]研究泡沫金属夹层以及涂胶泡沫金属夹层对自冲铆接头强度及失效形式的影响，分别制备了铝-铝、铝-泡沫铁镍夹层-铝和铝-涂胶泡沫铁镍夹层-铝的3种自冲铆接头，结果表明泡沫铁镍金属夹层和涂胶泡沫铁镍金属夹层可有效提高接头静失效载荷，但接头能量吸收值呈下降趋势。

以上研究主要集中在铆接孔周围应力分布对铆接件疲劳性能的影响。然而，关于铆钉剪切面内部残余应力对铆钉抗剪切性能研究仍然较少，探究铆钉剪切面处内部残余应力还没有得到足够的重视。本文分析不同孔径配合尺寸下，铆钉变形后对铆钉剪切面残余应力分布和大小的影响规律，以及剪切面处残余应力对铆接接头的剪切失效载荷的影响，并且通过试验对分析结果进行验证。

1 有限元仿真

1.1 材料模型

本文铆接使用的双层板材料为TC4钛合金，铆钉为304不锈钢，材料参数见表1。冲模较铆钉变形很小，视为刚体材料。钛合金板件规格为100 mm×25 mm×2 mm，板孔几何中心距搭接板长边12.5 mm。半圆头铆钉的直径为5 mm，杆长为10 mm。由于钛合金属于难加工材料，想要获得比较小的孔径差作为研究对比，制孔是一个难题，为了探究剪切面残余应力对铆钉抗剪强度的影响，铆接孔尺寸分别选择5.2、5.4、5.6 mm。各部件的几何关系如图1所示。

表1 TC4钛合金和304不锈钢铆钉的力学性能

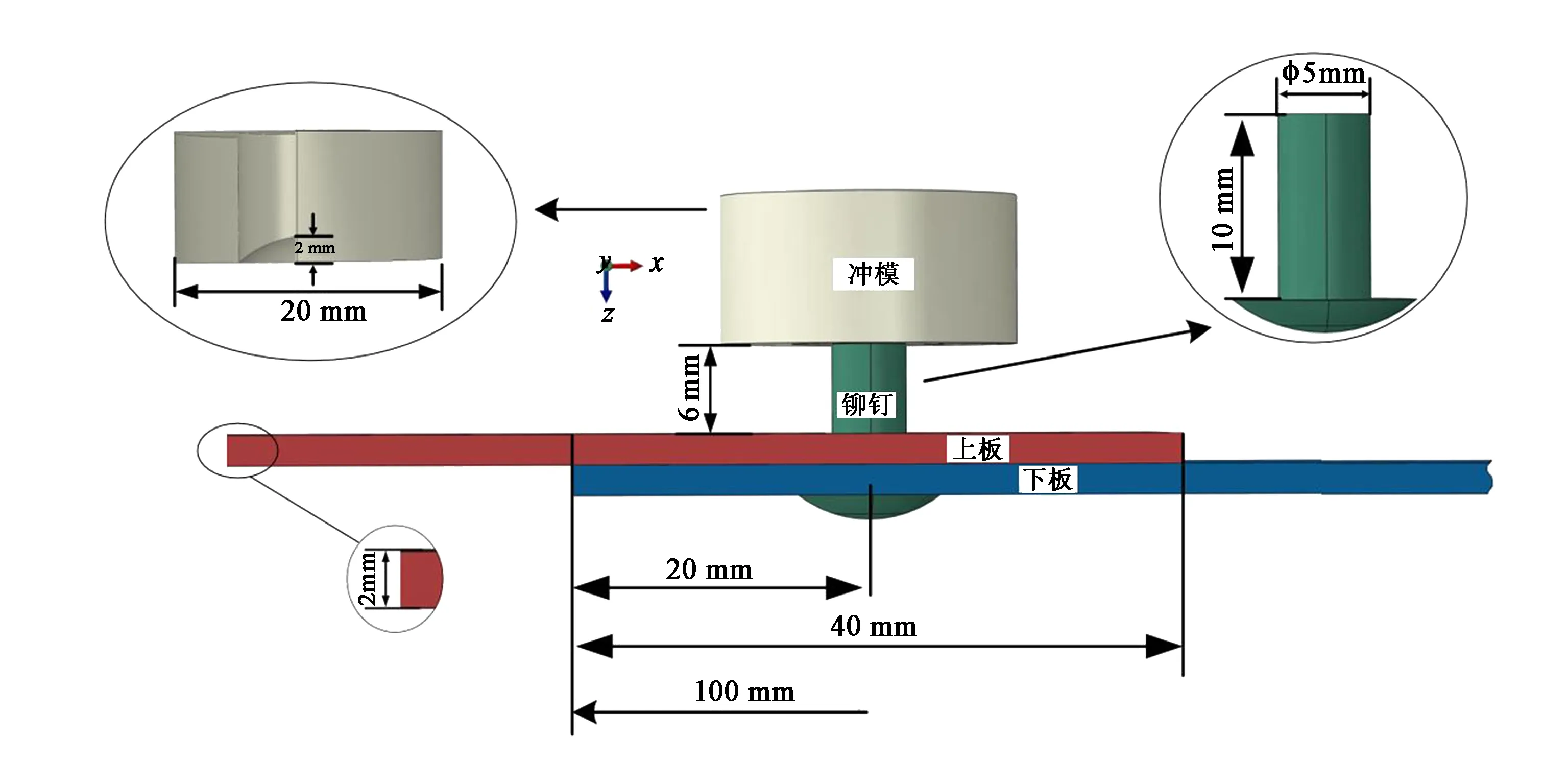
图1 双层板材搭接模型

采用有限元软件ABAQUS对板孔径尺寸分别为5.2、5.4、5.6 mm的双层TC4钛合金板进行铆接与剪切模拟。所有部件划分的单元类型为C3D8R，均采用六面体单元。因变形主要集中在铆接孔周围，采用六面体进阶算法对铆钉与板孔周围进行细化，其余部分采用六面体中性轴算法。整个网格模型的单元总数为554 756个，结点总数为584 752个，有限元划分模型如图2所示。

在进行剪切模拟时，需对铆钉材料添加损伤设置，304不锈钢材料属于断裂延性金属，选用韧性准则(Ductile criteria)。ABAQUS中提供的韧性准则需要输入的参数为：断裂应变、应力三轴度、应变速率，本文分别设置为0.1、0、0.001，采用损伤位移的形式对铆钉的损伤失效阶段进行演化，损伤位移设置为0.3。此外，有限元模型之间还存在以下接触关系：铆钉与连接板、铆钉与冲模、冲模与上板上表面、上板与下板贴合面的接触。使用ABAQUS提供的通用接触属性，所有表面之间的接触取摩擦因子为0.1。

图2 有限元模型网格划分

1.2 边界条件及载荷

根据研究内容将仿真划分为3个分析步，如图3所示。每个分析步均采用Dynamic Explicit算法。第一个分析步为铆接，冲模向下运动，使铆钉镦粗变形后与TC4两板发生干涉铆接。第二个分析步为冲模卸载，冲模卸载后，使墩粗铆钉部分发生弹性恢复，同时解除冲模对第三分析步造成的位移约束。第三个分析步为剪切失效，即将下板固定，对上板进行单向拉伸，直至铆钉剪切破坏。

第一、二个分析步中主要对冲模沿着z方向施加位移载荷，需对下板和铆钉扁圆头表面施加固定约束。冲模加载和卸载的位移分别为6、-5 mm，时间分别为0.1、0.01 s。第三个分析步对铆接件下板右端施加固定约束，上板左端施加沿负x方向的拉伸位移载荷，拉伸位移为5 mm，时间为1 s。

图3 各分析步边界条件及载荷施加

2 仿真结果分析

2.1 铆接过程

以孔径5.2 mm为例，铆接过程中铆钉与板材的变形情况及应力分布如图4所示，由图中可以看出，冲模接触铆钉头部开始，随着冲模下压，压铆力逐渐增大，使得铆钉开始发生变形，钉杆整体变粗。冲模位移继续增长，当钉杆接触到铆接孔边缘，铆钉与孔内壁接触区域开始变大，直至应力沿铆接孔厚度方向上均匀分布，此时铆钉杆与铆接孔周围面充分接触。随着冲模位移的增加，铆钉头部开始局部镦粗，形成墩头，冲模达到目标位移后，冲模停止运动，整个铆接过程完成。冲模卸载后，铆钉与孔周围材料发生弹性恢复，使得铆接头内部应力得到释放，但未能全部恢复，其内部仍存在残余应力。

2.2 孔径对干涉量的影响

干涉量是衡量铆接质量的一个重要指标。干涉量即为铆钉变形直径与初始铆接孔直径之差，其计算公式为

E=D-D0,

(1)

(2)

式中E为绝对干涉量(mm)，I为相对干涉量(%)，D为铆接后铆钉变形直径(mm)，D0为初始板孔直径(mm)。

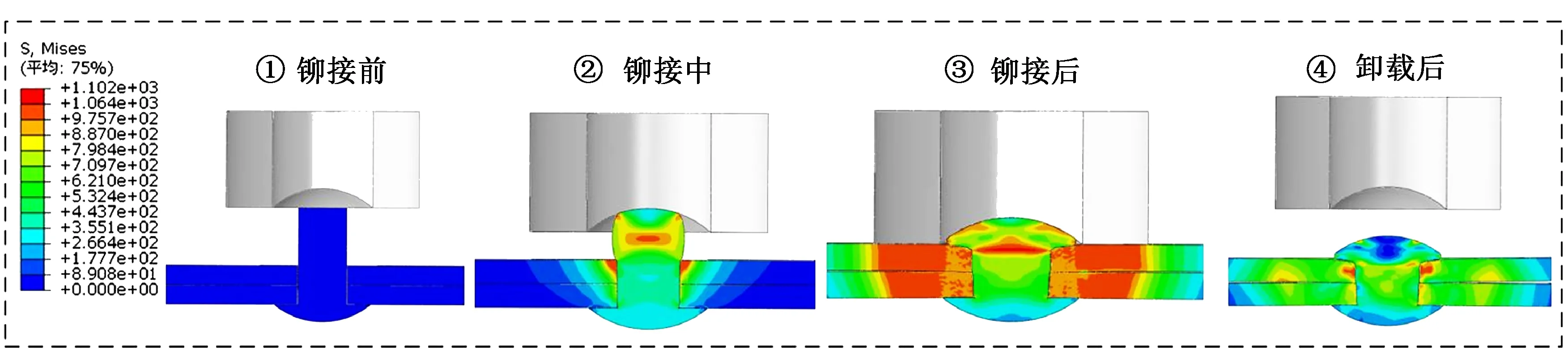
图4 孔径5.2 mm铆接过程应力云图

冲模作用下，铆钉顶端受力，铆钉材料流向孔内并且挤压孔壁形成一定干涉，但由于铆钉和板孔孔壁接触面存在摩擦，且沿铆钉轴向挤压力分布不均匀，造成干涉量和钉杆变形量沿轴向分布不均。为测量铆钉在冲模卸载后绝对干涉量大小，沿铆钉轴向每间隔0.4 mm，依次提取10个点，测得铆钉的变形直径，利用公式(1)计算得到绝对干涉量大小，10个点的位置如图5所示。

5.2、5.4、5.6 mm孔径的绝对干涉量分布如图6所示，结合图5可以看出，铆接后，绝对干涉量沿测量点1—10依次减少，最大干涉量为5.4 mm孔径，最小为5.6 mm孔径。上板上表面处铆钉变形最大，这是由于冲模一开始下降时铆钉与上板面挤压明显，使得上板上表面与墩头接触表面铆钉变形最大，随着距离的增加，铆钉对孔周围的挤压力逐渐减小，铆钉变形均呈现下降趋势。

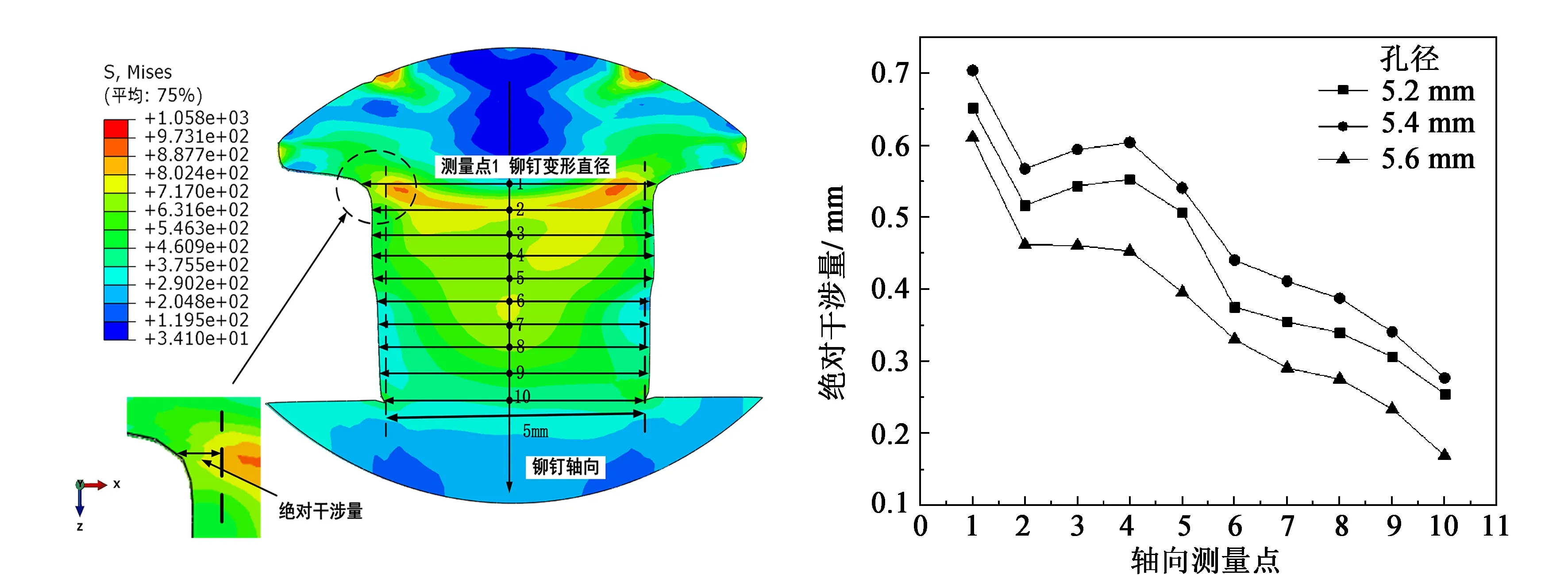
图5 铆钉钉杆直径测量位置示意图 图6 绝对干涉量

表2为不同孔径尺寸配合下铆钉变形后的平均干涉量大小，表中5.2、5.4、5.6 mm孔径的相对干涉量分别为8.5%、9.0%和6.6%，说明适当增大孔径配合间隙，可以加大铆钉材料向孔内的流动，增加铆钉对孔的干涉。在墩头成型时，若孔径配合尺寸过大，则难以使铆钉与孔壁之间形成较大的干涉。

表2 不同孔径下铆钉平均干涉量

2.3 剪切面残余应力对抗剪强度的影响

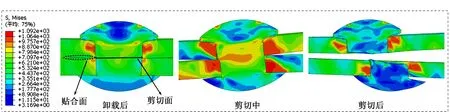
图7 5.2 mm孔径铆钉剪切失效过程应力云图

对铆接后的双层板材一端固定一端施加位移载荷，模拟剪切过程。以5.2 mm孔径为例，铆钉剪切失效过程如图7所示，当铆钉受剪力时，铆钉同时受到上板孔壁右侧和下板孔壁左侧的剪切力，此时铆钉在两板贴合面处的横截面为主要受力区，当达到铆钉的抗剪强度时，铆钉发生剪切破坏。仿真结果表明，当板材材料为TC4、铆钉材料为304、铆钉直径为5 mm时，铆钉主要发生剪切破坏，且铆钉破坏位置为上板和下板贴合面。如表3所示，测得5.2、5.4、5.6 mm孔径在剪切面处铆钉变形后直径分别为5.70、5.94、6.00 mm，模拟拉伸后铆钉的剪切失效载荷分别为13 780、15 510、15 160 N。

紧固件剪切力计算公式为[15]

F=4τ(πD2),

(3)

式中F为剪切力(N)，τ为剪切强度(MPa)，D为铆钉变形直径(mm)。根据公式(3)获得相应的理论剪切力，见表3。

表3 不同孔径剪切面参数

由式(3)分析，当铆钉剪切强度τ一定时，铆钉的抗剪切力F主要与剪切面积有关，即剪切面面积越大则剪切力越大。通过比较理论剪切力和仿真模拟剪切力，铆钉被剪断的最大剪切力并不随铆钉剪切面面积的增大而增大，其主要原因是铆钉剪切面的残余应力对其剪切强度有一定的影响，所以研究剪切面残余应力的分布对铆钉抗剪性能的影响意义重大。

图8为3种不同孔径尺寸沿钉杆轴向截面和剪切面Mises等效应力分布云图，可看出Mises等效应力主要分布在墩头与上板贴合面、铆钉与板孔接触面、上下板贴合面处。其中5.2 mm孔径等效应力主要分布在铆钉与板孔接触面，5.4 mm孔径主要分布在铆钉剪切面心部，5.6 mm孔径主要分布在铆接墩头与上板贴合面处。从剪切面圆心部可以看出，Mises等效应力分布集中的是5.4 mm孔径，其次为5.6 mm孔径，5.2 mm孔径最小。由此可得出，铆接孔径尺寸大小会影响铆接接头中的应力分布。

沿铆钉剪切面受力方向，从左到右依次提取剪切面中心线1—10结点的Mises等效应力数值，提取位置如图8所示，提取结果如图9所示。结合图8和图9可以看出，剪切面圆心部Mises等效应力比较集中，剪切面边缘由于和钉孔壁面接触，易发生弹性恢复，使应力得到释放，所以边缘处应力较小。Mises等效应力分布集中的是5.4 mm孔径，最大应力达到了900 MPa左右，其次为5.6 mm孔径，5.2 mm孔径最小。

图10为铆钉剪切面沿直径方向上1—10结点的S11(x向正应力)残余应力分布，由图可以看出，S11残余应力均为负值，表明剪切面单元在冲模卸载后受到的为压应力。剪切面处铆钉与孔壁表面接触附近(图中点3和8))残余应力较低，由剪切面边缘向圆心处方向残余压缩应力逐渐升高，5.2、5.4、5.6 mm孔径配合尺寸下，剪切面圆心部最小残余压缩应力分别为-283.1、-445.1、-428.1 MPa。结合图8可以得出，适当增大孔径配合尺寸，可以增加铆钉材料向钉头方向的流动，加大钉杆底部对孔壁的干涉，使铆钉破坏位置处的残余应力分布集中，从而提高铆钉抗剪强度。

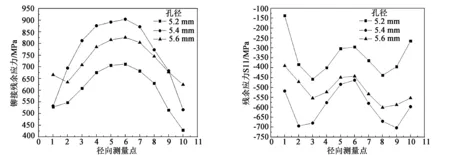
图9 铆钉剪切面沿正x方向单元结点铆接残余应力 图10 铆钉剪切面沿正x方向单元结点S11残余应力

3 试验验证

3.1 剪切试样制备

为了解残余应力对铆接试样静态强度的影响，分类进行了铆接试样剪切性能测试。试样分为D1、D30组，D1组对不同孔径尺寸铆接后放置1 d就进行拉伸剪切试验，D30则在铆接后自然放置30 d，采用自然时效的方法对铆钉内部残余应力达到一定消除，再进行拉伸剪切试验，试验方案见表4。

表4 剪切试验方案

利用压铆法将铆接元件和板材连接起来，冲模与仿真模拟同样采用位移控制，下压位移为6 mm，图11为5.2、5.4、5.6 mm孔径尺寸铆接好的试样。

在微机控制万能试验机(WAW-300)上进行准静态剪切试验，如图12所示，试验过程中单轴拉伸试验的拉伸速率设置为2.5 mm/min，试样破坏后终止加载。

图11 铆接试样 图12 剪切试验

3.2 试验结果与分析

由图13中两组试样发生剪切后载荷和位移的关系，可以看出3种孔径接头的剪切力与位移曲线和失效过程基本一致，但其峰值有一定的差别。整个过程分为3个阶段：第一阶段是弹性阶段，3条曲线重合性较高，载荷以相同的速率快速增长；第二阶段是屈服阶段，剪切力增速较慢，第三阶段是失效阶段，铆钉发生断裂。

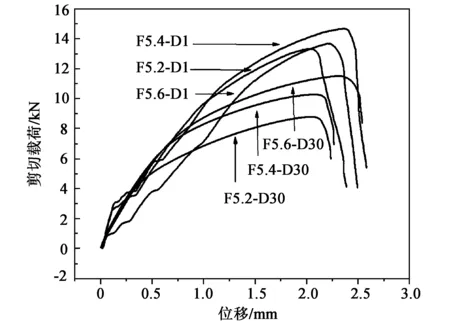
图13 不同孔径剪切载荷-位移曲线

金属材料长时间的自然时效会使材料的硬度、残余应力与线膨胀率都逐渐降低[16]。在未经过自然时效处理的试样组中，5.4 mm孔径所能承受的抗剪强度最高，这与仿真模拟规律一致；5.2、5.4、5.6 mm孔径的最大剪切失效载荷为13.3、14.7、13.7 kN，各孔径与仿真得出的最大失效剪切载荷误差分别为6.0%、5.5%、10.6%。试样经过放置30 d后，剪切载荷降低了近30%左右。仿真与试验结果都表明，铆钉剪切面的残余应力对铆钉的抗剪强度有一定提高。

4 结论

(1)通过有限元模拟，说明适当增大孔径配合间隙，可以加大铆钉材料向孔内的流动，增加铆钉对孔的干涉；若孔径配合间隙过大，则难以使铆钉与孔壁之间形成较大的干涉，使得铆接件的承载性能下降。

(2)通过有限元模拟，铆接接头在受到大的拉伸载荷作用时，铆接接头主要以铆钉被剪断而失效。冲模卸载后，铆钉剪切面主要受到的Mises等效应力主要分布在剪切面圆心部，压缩残余应力主要分布在剪切面边缘。不同铆接孔直径可以使铆钉内部残余应力大小发生改变，模拟得到5.4 mm孔径剪切面残余应力和剪切载荷最大。

(3)通过剪切试验，对比未时效处理和时效处理后剪切力大小，发现经过时效处理的铆接接头处残余应力明显减小，铆钉抗剪强度也随着铆钉剪切面残余应力的下降而降低，验证了仿真模拟的正确性。