钢筋混凝土矩形梁正截面承载能力计算研究

邬文祥 陈顺超 陈 杰 熊竑瑞 李正垣 聂良鹏

（1.西南林业大学土木工程学院，云南 昆明 650224；2.云南通衢工程检测有限公司，云南 昆明 650200）

0 引言

钢筋混凝土矩形梁是结构中最为典型的受弯构件，在桥梁工程中应用非常广泛［1］。在设计时，由于混凝土的变形呈非线性［2］，为了方便计算，各国相关规范都对混凝土受压区应力—应变关系曲线进行了相应的简化。我国的《混凝土结构设计规范》（GB 50010—2010）（2015版）通过把受压区混凝土应力—应变关系曲线简化成矩形，从而推导出计算截面的抗弯承载能力Mu［3］，这种方法具有计算简便、快捷等优点［4］。但在计算时将混凝土压应力分布曲线等效成矩形，相关材料参数取设计值进行计算，往往忽视了材料实测强度、混凝土压区应力—应变关系为曲线时对承载能力的影响。

本研究利用混凝土压区应力—应变曲线、实测材料参数，推导出混凝土受压区合力C 以及抗弯承载能力Ms的公式，与《混凝土结构设计规范》（GB 50010—2010）（2015 版）抗弯承载能力Mu、试验结果加之比较，从而分析实测材料参数、混凝土压区应力—应变分布为曲线时对混凝土矩形梁正截面承载能力的影响。

1 极限承载能力计算

1.1 假定

基于文献［5］得出如下假定：①在荷载作用下，截面变形后保持为平面；②不考虑混凝土的抗拉强度；③钢筋、混凝土的应力—应变图已知。

1.2 钢筋混凝土梁极限状态的一般规律

一是受拉区混凝土开裂，继而退出工作，拉力由钢筋承担；二是受拉钢筋先达到屈服强度，且应力不变，应变明显增大；三是梁的受压区边缘混凝土在钢筋达到屈服强度后，逐渐达到极限压应变，随着荷载增大梁随之破坏［6］。

1.3 按规范计算——规范法

《混凝土结构设计规范》（GB 50010—2010）（2015 版）和《混凝土结构设计原理》［7］对钢筋混凝土矩形梁正截面承载能力的计算做出了详细规定（见图1）。其基本思想是：先根据实际情况预先求出设计截面抗弯承载能力Md；再利用相应规范，选用材料设计强度计算出截面极限抗弯承载力Mu。若钢筋抗拉强度设计值fsd、混凝土轴心抗压强度设计值fcd、截面尺寸b、纵向受拉区全部钢筋截面面积As已知，则可根据式（1）求出受压区名义高度x。

图1 按规范计算图示

从而根据式（2）求出计算截面的抗弯极限承载力Mu。

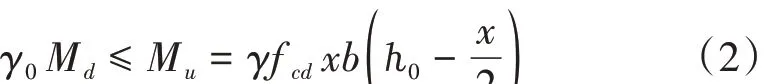
式中：β 为混凝土名义压区高度与实际压区高度换算系数；γ 为等效矩形混凝土抗压强度换算系数；γ0为结构重要性系数；ℎ0为截面有效高度。

1.4 基于曲线积分法计算——积分法

若按规范所述方法进行计算，由于材料设计值与实测值相差较大，现尝试利用材料实测强度直接对应力—应变曲线进行积分，进而得到基于实测材料参数的钢筋混凝土矩形梁极限承载力Ms。具体计算过程如下，受压区截面应力—应变关系见图2。

图2 积分法计算图示

①基于平截面假定，假定受压区分布服从相似规律可以得到，离中和轴的距离x 对应的混凝土应变关系表达如式（3）。

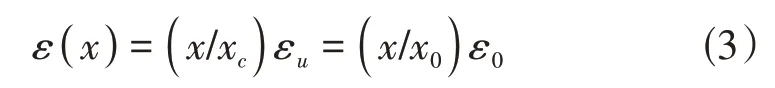
式中：xc为混凝土实际受压区高度；εu为混凝土的极限压应变；ε0为混凝土峰值应力时对应的应变。

②众多学者对混凝土单向受压变形特征做了大量试验，其中CEB/FIB 模型［8］，考虑到混凝土初始弹性模量、峰值应力处弹性模量对曲线的影响，因而在上升段能较好地满足混凝土经典曲线［9］，清华大学用αd表示不同材料和强度的混凝土对下降段曲线的影响，能相对较好地反映混凝土受压区的应力应变关系［10］。所以本研究中混凝土受压区应力—应变曲线上升段取CEB/FIB 模型，下降段取清华大学模型［11］，进而推导出截面抗弯承载能力Ms的公式。

混凝土受压区应力—应变关系模型如式（4）。

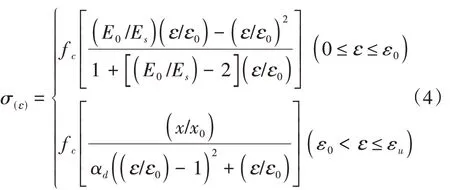
式中：fc为混凝土峰值应力；ES为混凝土割线模量；E0为混凝土弹性模量；αd为不同材料和强度的混凝土对下降段曲线的影响系数，根据文献［11］得αd为0.4。

其中混凝土的割线模量与原点弹性模量的关系为式（5）。

式中：λ 为弹性特征系数即 λ = εce/εK，当σ(ɛ) ≤0.5f c 时，λ ≈ 0.9，εce 为弹性应变，εK 为割线模量时混凝土应变，本研究λ取0.9。

根据中和轴距离x 与其对应的混凝土应变关系式ε(x )和式（5）可以得到任意受压区高度x 对应的压应力σ（见图3）如式（6）。

图3 受压区高度与应力关系

利用式（6）对σ(x ) 进行积分求得合力C如式（7）。

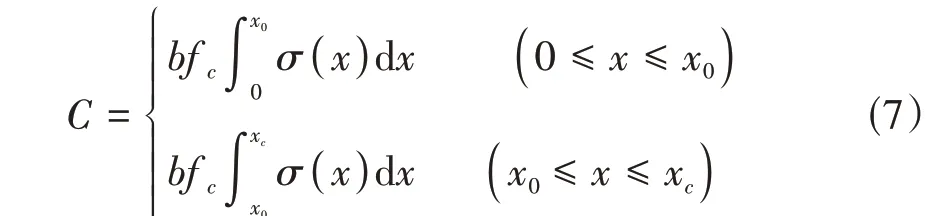
根据我国规范 εcu取 0.003 3，ε0取 0.002，将式（6）代入式（7），令t = x/x0，N = E0/Es，得式（8）。

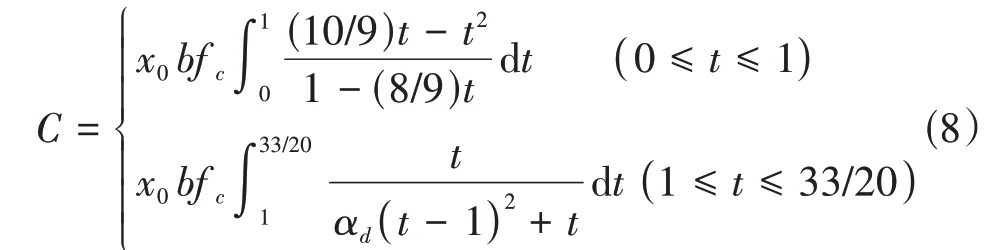
式中：b为截面宽度。对式（8）积分得式（9）。

③假定梁处于适筋破坏，受拉区钢筋则刚好可以达到屈服强度，即钢筋的拉应力与混凝土压应力合力C 满足如下关系式，即可求得混凝土实际受压区高度xc，如式（10）。

式中：As为受拉钢筋截面面积之和；fs为钢筋实测屈服强度。

④利用上式可求得合力C 的作用点到截面受压边缘的距离 xs［12］，如式（11）。

化简得式（12）。

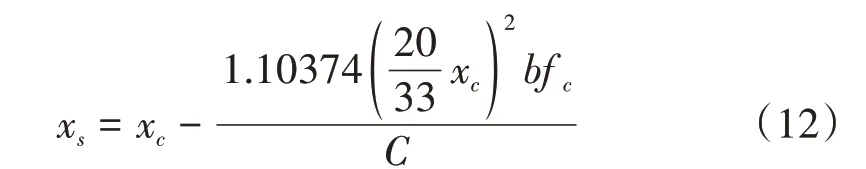
⑤根据截面力学平衡条件建立如式（13）等式，分别求得截面抗弯承载能力Ms。

综上所述，可以得到混凝土实际受压区高度对应的抗弯承载能力。

1.5 取实测值计算

实测立方体抗压强度fc= 40.9 MPa，钢筋实测强度fs1= 480 MPa、fs2= 540 MPa，混凝土受压区截面宽度b = 120 mm，截面高度ℎ = 160 mm、as=30 mm，钢筋公称直径r1= 8 mm、12 mm。

按规范所述计算方法具体的计算步骤在规范中已详细给出，不再赘述，其计算结果见表1。

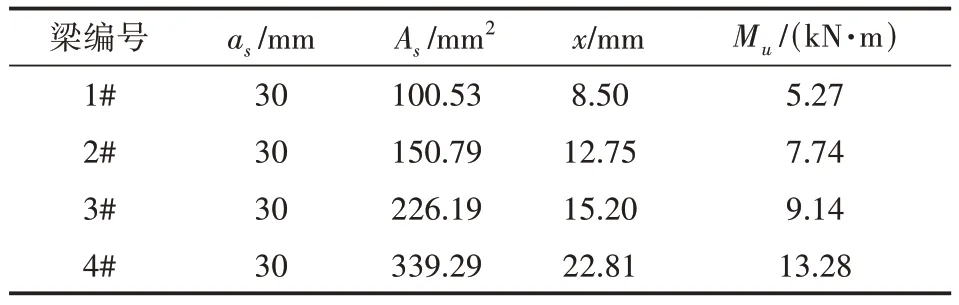
表1 按规范计算抗弯承载力

将以上取值分别代入式（9）、式（10）、式（12）、式（13），求得受压区合力C。假定梁处于适筋范围，由钢筋的拉应力合力与混凝土压应力合力C 满足式（10），可分别求得实际受压区高度xc。根据式（12）求得合力作用点C 到截面受压区边缘的距离为xs。将xs、C、ℎ0分别代入式（13）可以得到截面抗弯承载能力。以上计算过程的计算结果如表2所示。

表2 积分法取实测值计算结果

2 试验

2.1 试验材料以及试验梁的基本参数

以计算取值为例，试验采用强度等级为32.5 R的普通硅酸盐水泥，强度为C45 的混凝土。制作4组试件按照标准［13］养护28 d后，实测平均力学参数如表3 所示。钢筋选用牌号为HRB400，HRB500，实测平均抗拉强度如表4 所示。制作4 根尺寸为1 280 mm×160 mm×120 mm、计算跨径为1 080 mm的钢筋混凝土简支梁（见图4）。其他参数如表5所示。

图4 混凝土简支梁截面图（单位：mm）

表3 混凝土实测力学性能

表4 钢筋实测力学性能

表5 梁其他参数

2.2 加载

如图5 所示的装置，采用三等分加载，间距为3 mm×360 mm。在竖向千斤顶之间配置压力传感器，根据《混凝土结构试验方法标准》（GB/T 50152—2012）［14］进行加载。试验所得梁的极限荷载见表6。

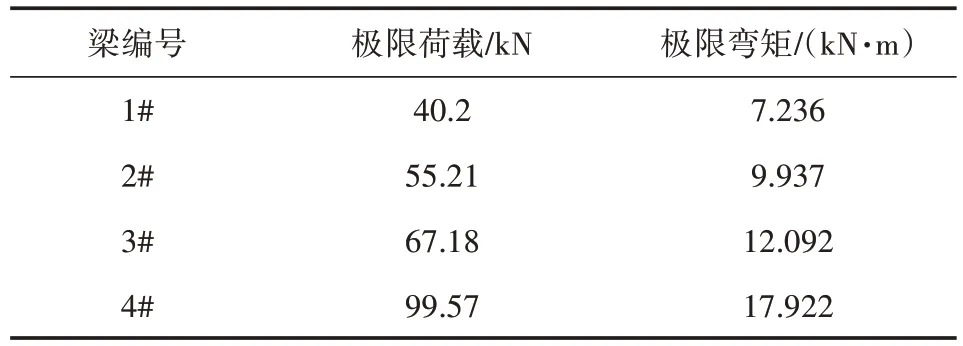
表6 梁试验数据表

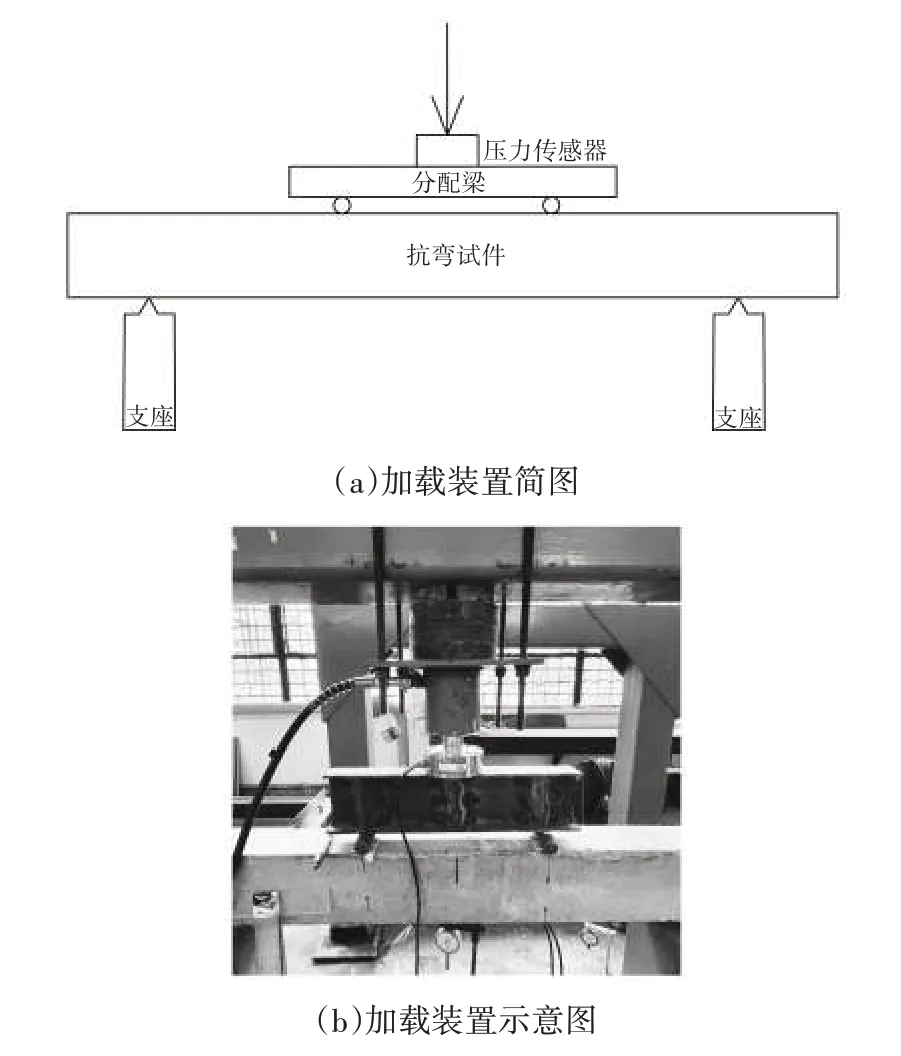
图5 装置加载图

3 对比分析

将抗弯承载能力进行比较，如表7、图6 所示，发现两种计算方法计算出的抗弯承载能力结果差别较大，配筋率越高误差越大，两者相对误差保持在24.27%~32.96%，按规范计算出的承载力和试验测得承载力误差较大，两者误差为29.93%~33.00%，说明按照规范计算出的承载能力结果偏于保守。用积分法计算出的抗弯承载力和试验测得抗弯承载力差别较小，两者误差仅为0.06%~7.47%。分析其原因，在两种方法计算过程中，规范计算取用材料强度设计值fsd、fcd，而积分计算法则是取用通过试验得到实测材料强度fs1= 540 MPa、fs2= 480 MPa，显然实测值与设计值误差较大。

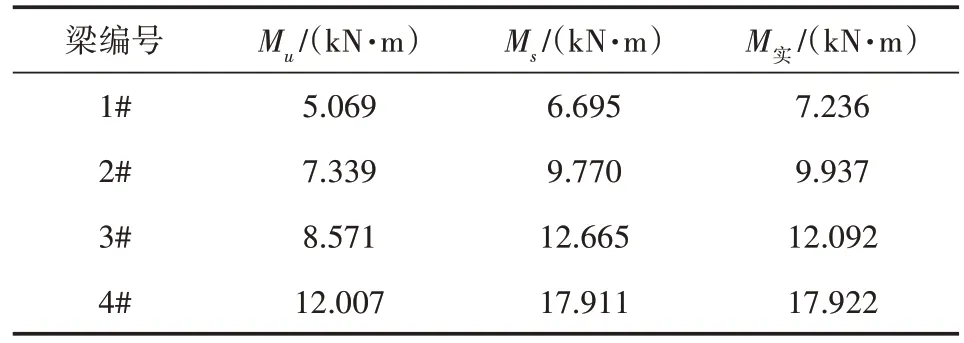
表7 两种计算结果与试验结果对比

图6 两种计算结果与试验对比

将规范计算抗弯承载力中的钢筋屈服强度、混凝土轴心抗压强度均取用实测值，进行计算的结果如表8、图7所示。

由表8、图7 可知，在材料强度取实测值之后，规范法和积分法计算出的结果误差较小，误差仅为0.82%~2.77%，吻合程度较高。此外，积分法与试验测得承载力误差较小，保持在0.06%~7.47%，规范法计算承载能力与试验测得承载力，保持在0.42%~6.71%。显然，不同的混凝土受压区应力—应变曲线，对混凝土矩形梁截面承载能力大小有影响。

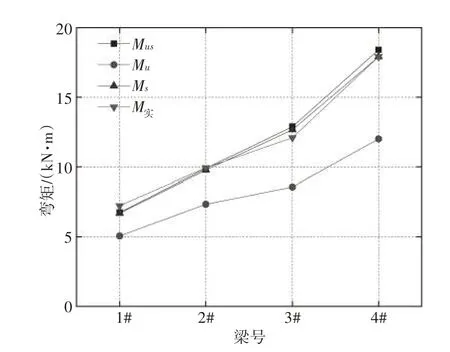
图7 材料实测参数用规范法计算结果对照

表8 取材料实测值参数用规范法计算结果对照

4 结论

①针对《混凝土结构设计规范》和《混凝土结构设计原理》中关于钢筋混凝土梁正截面承载能力部分，对设计值与材料参数实测值计算结果进行了比较，发现用设计值计算出的结果强度储备高且误差较大。

②在结构满足平截面假定的基础上，介绍了基于曲线积分，给出针对不同混凝土应力—应变模型计算钢筋混凝土矩形梁抗弯承载能力的公式。

③材料强度选用实测参数时，将规范法和积分法计算的结果与试验实测结果进行了比较分析，发现2 种计算方法的相对误差较小，误差最高为2.77%，说明积分法能较为准确地适用正截面承载能力计算。

④因积分法和规范法均可用于钢筋混凝土矩形梁极限承载能力计算，若在设计时将两种方法计算的结果应用在实际工程中，可为实际工程设计提供一定的参考依据。