基于夹点理论的人工冰场CO2制冷热回收系统优化分析

周啸虎 耿旭东 李 锋 司春强 马 进 邵双全

（1 华中科技大学能源与动力工程学院 武汉 430074；2 华商国际工程有限公司 北京 100069）

近年来，环境问题已逐渐成为全球关注的焦点之一，而我国作为当今最大的碳排放国家一直致力于减少氢氟烃的排放以及寻找清洁能源[1]。制冷行业作为制造业中的重要组成部分，能耗高，节能减排的潜力巨大。其中，人工冰场是能耗较高的建筑之一[2]。因此，降低人工冰场能耗能极大促进节能减排的实现，关键在于换用节能环保的制冷剂和采用高效的制冷系统配置。CO2作为自然工质，具有安全性、环保性、优越的热力学性能等优点[3]，逐渐受到人们的广泛关注，并应用于热泵[4]、汽车空调[5]、超市[6]、冷藏车[7]等领域。自1999年建造了第一个使用CO2作为载冷剂的人工冰场[8]以来，CO2也开始被用于人工冰场行业。虽然优点众多，CO2仍存在临界温度较低的问题。当环境温度较高时，CO2制冷系统处于跨临界循环运行时的效率较低[9]。因此，许多研究致力于提高CO2制冷系统的性能，如使用热电过冷[10]和机械过冷[11]增加过冷度，使用多级压缩[12]和并行压缩[13]降低压缩机功耗，使用涡管[14]、膨胀机[15]和喷射器[16]代替膨胀阀减少节流损失。因此，本文采用喷射器和并行压缩同时改进的系统应用于人工冰场进行分析。

人工冰场除了常规的制冷需要，还有较多制热需求，包括生活热水、除湿再生、通风供暖等[17]，而CO2高热回收潜力刚好可以满足人工冰场的部分甚至全部需求。因此人工冰场的CO2制冷热回收系统相当于制冷及热泵系统进行结合，可极大降低能耗。

但超临界状态下的CO2在换热时会出现温度滑移，导致水冷式换热器产生夹点，从而限制换热性能及出水温度[18]。热泵系统中传统的热力学分析中常以固定气冷器出口温度模型来计算系统性能（本系统中应为固定热回收换热器CO2出口温度），从而忽略了夹点的影响。因此，Chen Yunguang[19-20]使用夹点分析法对CO2热泵热水器进行热力学分析，得出有关参数对系统换热的影响规律，并分析夹点对CO2热泵最佳排热压力的影响。

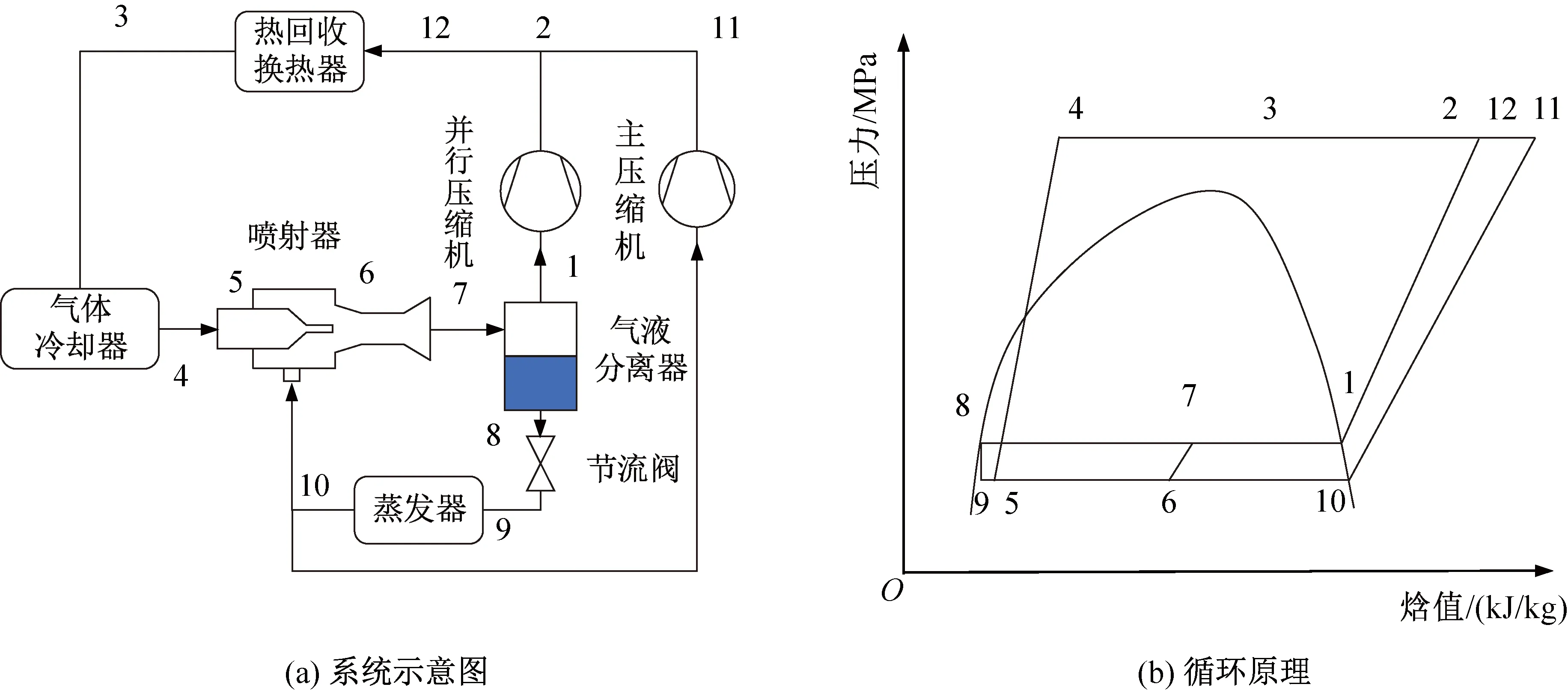
图1 并行压缩喷射制冷系统Fig.1 Parallel compression ejector expansion refrigeration cycle

因此，以人工冰场改进的CO2制冷热回收系统为背景，基于夹点分析理论，本文对人工冰场CO2制冷热回收系统进行了优化分析，并与理论计算结果进行对比，得到夹点对该系统有关参数及性能的影响，从而更好的指导热回收的控制以提升系统性能。

1 人工冰场CO2制冷热回收系统模型建立

1.1 循环描述

本文人工冰场CO2制冷热回收系统为并行压缩喷射制冷系统（parallel compression ejector expansion refrigeration cycle，PCEERC），系统示意图和循环原理如图1所示。该系统循环包括两个压缩机、气体冷却器、气液分离器、节流阀、蒸发器、热回收换热器和喷射器。循环工作原理如下：主压缩机和并行压缩机出口的制冷剂混合（状态12），经过热回收热交换器（在单独制冷模式下，热回收热交换器将旁通）和气体冷却器冷却（冷凝器）（状态4），进入喷射器的主喷嘴中膨胀加速（状态5），并引射来自蒸发器的部分流体（状态10）。然后两种流体在混合室内恒压混合（状态6），在扩散器中扩散，其中动能转换为压力势能（状态7）。最后，将两相流体从喷射器排出，进入气液分离器，分离成饱和液体（状态8）和气体（状态1）。其中，饱和液体进入节流阀节流成低压流体（状态9），然后进入蒸发器。而饱和气体通过并行压缩机进行压缩（状态2）。同时，来自蒸发器出口流体的另一部分进入主压缩机（状态11），主压缩机与来自平行压缩机的流体混合并继续循环。

1.2 热力学模型

本文从质量、动量和能量守恒的角度对循环的每个过程进行能量分析，从而建立热力学模型，其中喷射器采用一维恒压混合模型。

为简化热力学模型，进行如下假设：

1）所有部件均处于稳态运行，流体在喷射器中处于一维流动；

2）气液分离器和蒸发器出口均为饱和流体，制冷剂在膨胀阀节流前后焓值相等；

3）管道中的压降和热、流量损失均忽略不计；

4）混合过程发生在混合室中，恒压等于蒸发压力，喷射器进出口处的速度忽略不计；

5）在喷射器中，喷嘴效率ηn为0.8，混合效率ηm为0.95，扩散效率ηd为0.8[21]；

6）制冷量Q0为20 kW，蒸发温度Te为-20 ℃，若无特殊说明，蒸发器出口的两股流体质量流量比为1；

7）假设两级串联热回收，低温级进、出口水温为40 ℃和60 ℃，高温级为60 ℃和80 ℃；

8）压缩机最高排气温度为160 ℃，最高排气压力为11 MPa；

9）假设环境温度为35 ℃，换热器的夹点温差为3 ℃，因此气冷器出口温度为38 ℃；理论的热回收换热器出口温度T3为43 ℃。

喷射器的引射系数μ：

（1）

式中：m10，e为蒸发器出口流向喷射器的二次流体质量流量，kg/s。

设蒸发器出口流向压缩机的流体与流向喷射器的流体的质量流量之比β为：

（2）

式中：m10,c为蒸发器流向压缩机流体的质量流量，kg/s。

压缩机的等熵效率ηcom：

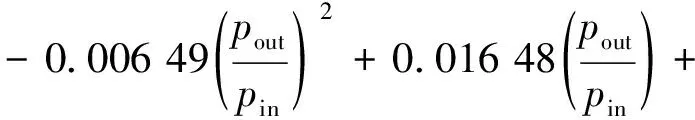
0.664 6

（3）

蒸发器处的制冷剂质量流量m10：

（4）

结合μ和β可求得其它部件的质量流量（包括m10,e、m1、m4），主压缩机、并行压缩机及总功耗为：

W10,com=m10,e（h11-h10）

（5）

W1,com=m1（h2-h1）

（6）

W=W10,com+W1,com

（7）

热回收量：

Qhr=m4（h12-h3）

（8）

系统的制冷性能系数、制热性能系数以及综合性能系数为：

（9）

（10）

（11）

2 夹点分析计算模型

图2所示为两级串联热回收的换热情况。

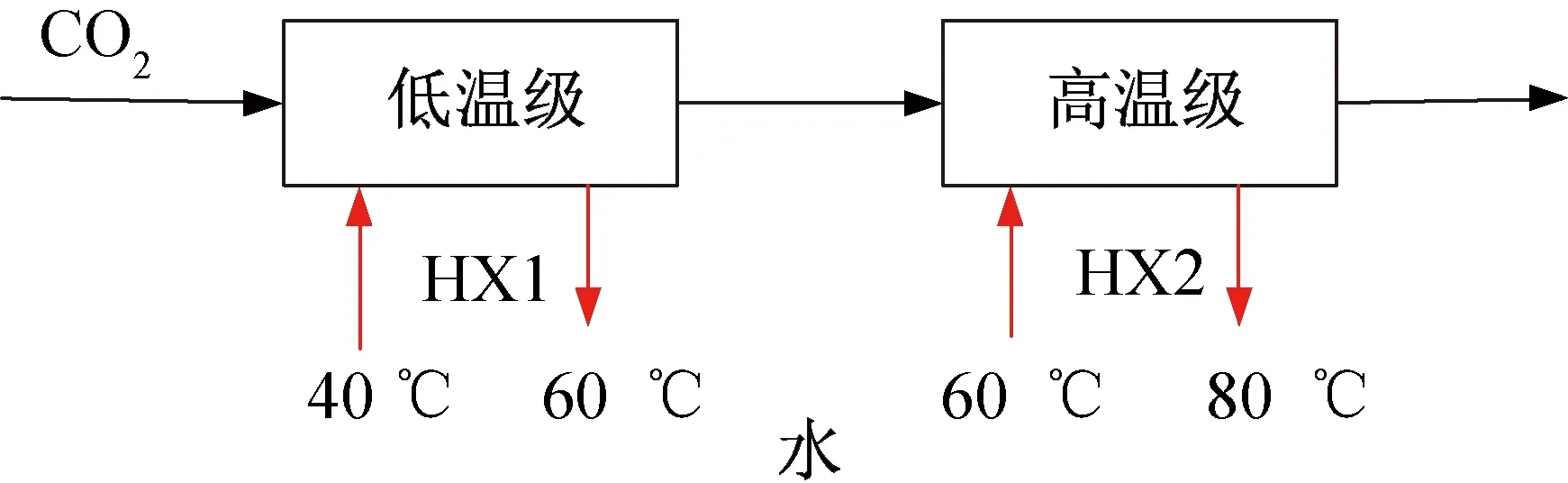
图2 两级热回收示意图Fig.2 Schematic diagram of two-stage heat recovery

理论情况下热回收换热器CO2出口温度T4为43 ℃，实际上由于夹点的限制，热回收换热器的出口CO2温度一般高于43 ℃，从而影响热回收量和制热性能系数甚至综合COP，但对制冷性能系数并无影响，因此后续性能分析不包括制冷性能系数。在本文假设工况下（进出口水温固定），可通过调节高低温级的水质量流量来改变夹点的位置从而调节T4，本文采用的分析方法为T-Q图分析，如图3所示，图中换热曲线的斜率为热容（比热容乘以质量流量）的倒数，不同取水段的进出口水温顺接。可以看出高低温的水质量流量变化会影响T4。

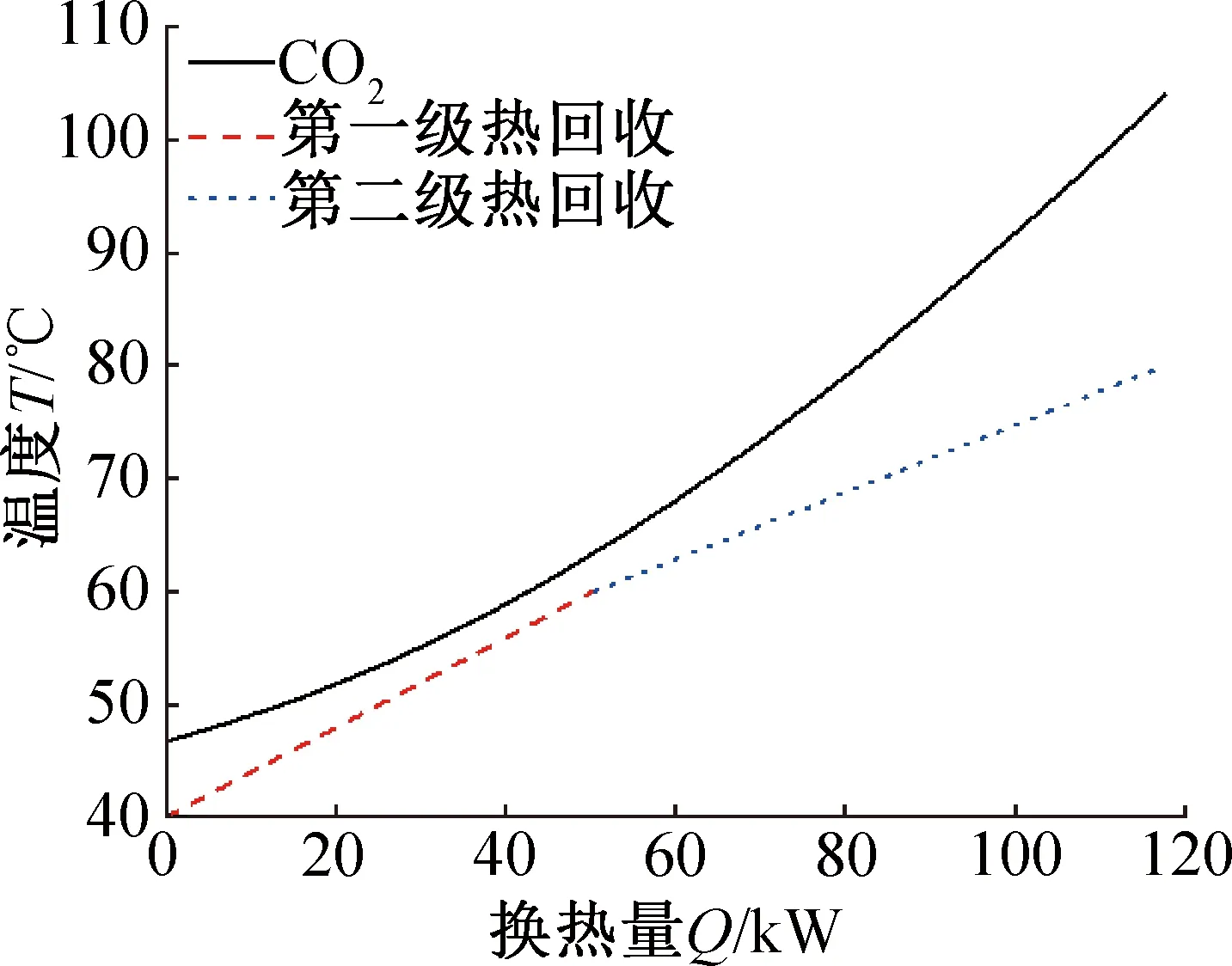
图3 T-Q图Fig.3 T-Q figure

在不同排气压力下，CO2换热曲线中的近临界点和近临界温度也是主要影响因素。图4所示为不同排气压力下CO2比热容随温度和压力的变化。可以看出，排气压力越高，除整体热容降低外，热容的最高峰对应的温度（近临界温度）越大，当排气压力由7.5 MPa增至11 MPa，近临界点温度由32 ℃升至约50 ℃。

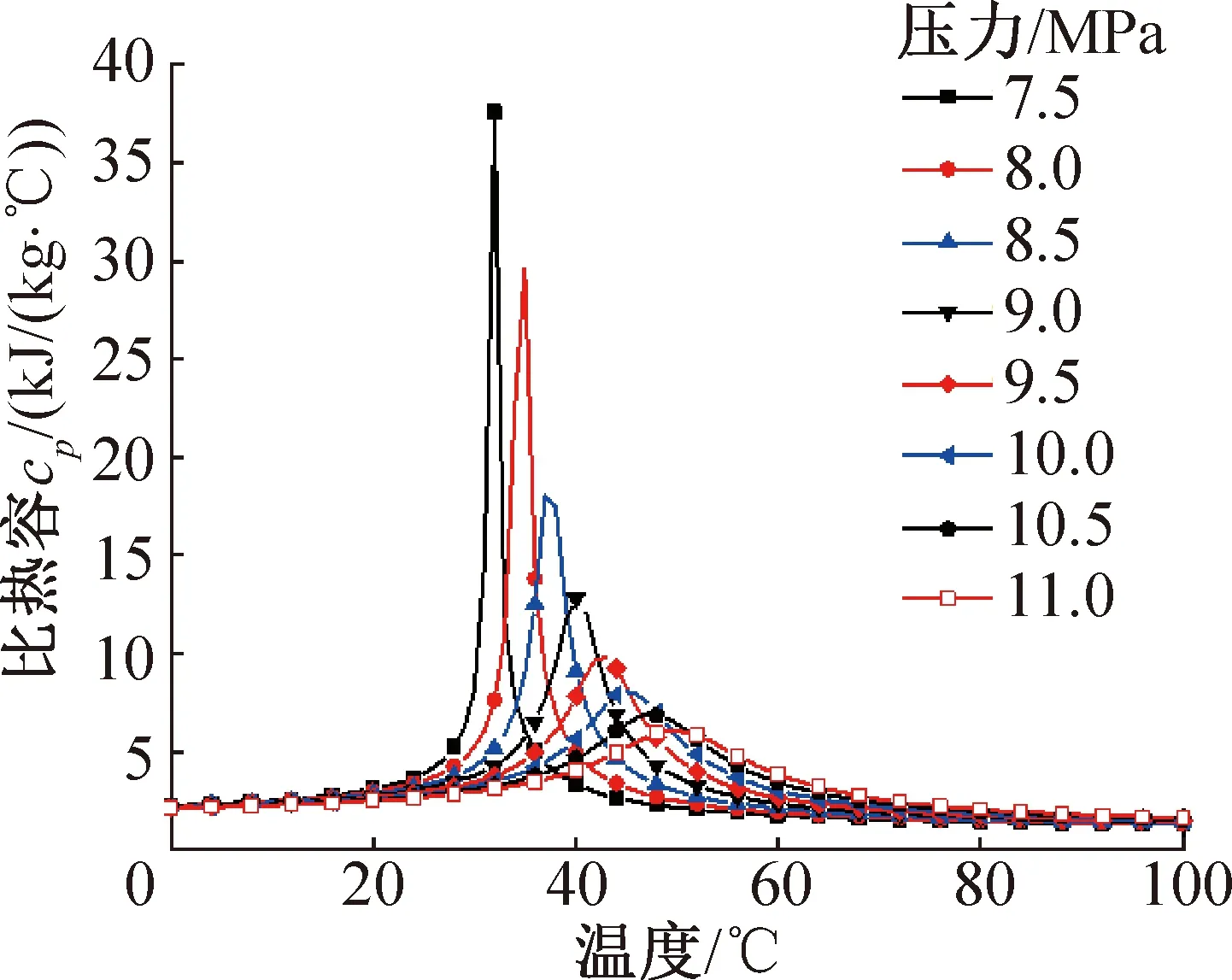
图4 CO2比热容随温度和压力的变化Fig.4 Specific heat capacity of CO2 varies with temperature and pressure

为了更好地分析不同进水质量流量或水与CO2的质量流量比对夹点的影响，以及对整体系统循环性能的影响，此时并不固定制热量，主要分析水与CO2的质量流量比对CO2出口温度及整个系统的影响。计算方法为：假设某一级质量流量比渐变时，另一级的质量流量比对应以尽量减小CO2出口温度为优化目标进行选取。

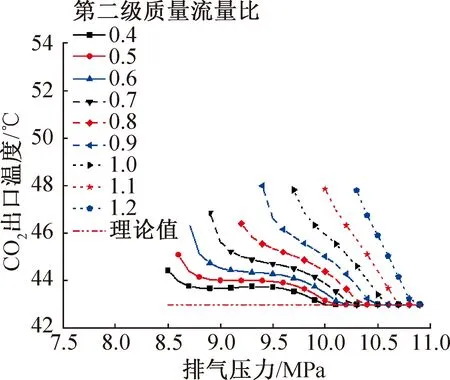
图5 不同第二级质量流量比下CO2出口温度随排气压力的变化Fig.5 Variation of CO2 outlet temperature with discharge pressure under different second stage mass flow ratio

3 结果与分析

3.1 第二级质量流量比渐变

图5所示为不同排气压力和第二级质量流量比的CO2出口温度变化。可以看出，当第二级质量流量比越大时，高温级换热区域温度滑移匹配越差，因此需要通过提升排气压力来提高CO2的进口温度，从而满足80 ℃的供水温度，即能够开始进行热回收所需的排气压力会越高。

同时，在刚好能进行热回收的排气压力下时，质量流量比越大，CO2出口的温度整体均升高，说明当第二级热回收处的温差较小时（夹点出现在第二级热回收），第二级热容的不匹配程度也会影响第一级的热容匹配，从而使CO2出口温度无法有效降低；而在排气压力逐渐升高之后，多数质量流量比下的CO2出口温度均趋于理论值，说明当第二级热回收的温差较大时（夹点不在第二级热回收处），第二级质量流量比对第一级的热容匹配的影响很小，第二级的质量流量比基本均能调节使CO2出口温度为理论最佳值。

图6所示为第一级质量流量比随第二级质量比和排气压力的变化。可以看出，第一级质量流量比随排气压力的升高和第二级质量流量比的降低而增大。当排气压力升高时，需要升高第一级质量流量比来降低CO2出口温度。

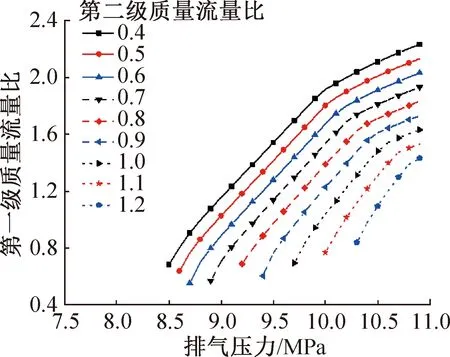
图6 不同第二级质量流量比下第一级质量流量比随排气压力的变化Fig.6 Variation of first stage mass flow ratio with discharge pressure under different second stage mass flow ratio

由于CO2出口温度受到影响，使制热性能系数和综合性能系数均受影响。

图7所示为热回收量的变化情况，理论情况下，热回收量会随排气压力的升高先降低再升高，但考虑夹点时，排气压力升高会使CO2出口温度降低，导致热回收单位焓差升高，给热回收带来一定的增益，该增益在低排气压力下更显著（此时升高排气压力会使CO2出口温度显著降低），因此本应降低的热回收量此时也升高了，导致在某一质量流量比下的热回收量只会随排气压力的升高而升高。总体而言，第二级质量流量比越大，热回收量越小。

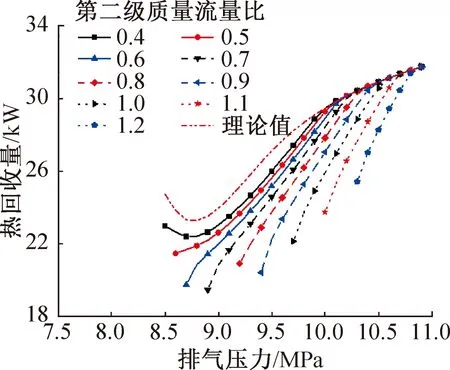
图7 不同第二级质量流量比下热回收量随排气压力的变化Fig.7 Variation of heat recovery with discharge pressure under different second stage mass flow ratio

图8所示为制热COP的变化情况。可以看出，变化趋势与热回收量基本一致，第二级质量流量比越大时，制热COP越小，区别是，随着第二级质量流量比升高，初始可热回收排气压力升高，初始可进行热回收下的制热COP也呈先减再增的趋势，与热回收量先减后增的趋势相同，但程度更轻，原因是压缩机功耗会先减后增。

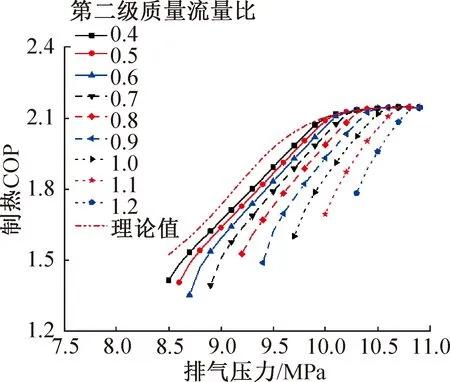
图8 不同第二级质量流量比下制热COP随排气压力的变化Fig.8 Variation of heat coefficient of performance with discharge pressure under different second stage mass flow ratio

图9所示为综合COP的变化情况，前期COP在不同质量流量比下相等的原因是没有热回收，COP即制冷性能系数，而不同质量流量所影响的CO2热回收出口温度对制冷性能系数并无影响。随着第二级质量流量比的升高，一方面初始可热回收对应的排气压力下的COP升高，且整体COP均降低；随着第二级质量流量比的升高，最大COP对应的最佳排气压力也向后移动，超过限制的最大排气压力。理论情况下，最大综合COP为3.538，对应的排气压力为10.2 MPa，在夹点的影响下，当第二级质量流量比为0.4时，因在10.2 MPa下的CO2出口温度仍能优化达到43 ℃，此时最佳排气压力和最大综合COP与理论值一致；而当第二级质量流量比为1.2时，由于CO2出口温度无法得到有效降低，此时最佳排气压力成为受限下的最大值10.9 MPa（11 MPa时，压缩机排气温度超出上限），最大综合COP仅为3.496。

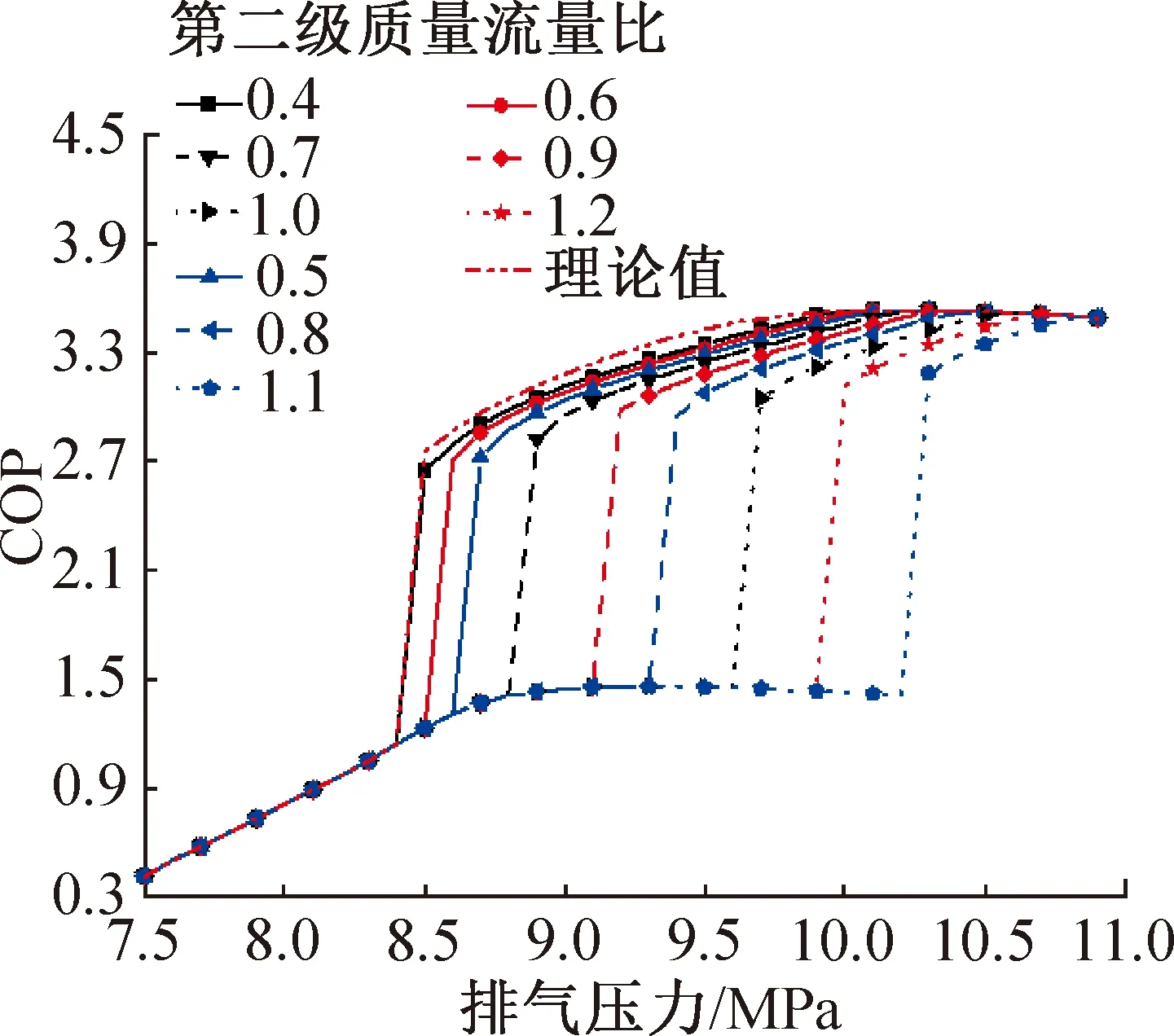
图9 不同第二级质量流量比下综合COP随排气压力的变化Fig.9 Variation of comprehensive coefficient of performance with discharge pressure under different second stage mass flow ratio

综上可知，在第二级质量比渐变，调节第一级质量流量比使CO2出口温度最低的情况下，第二级质量流量比越大，对系统性能的损害越大，使CO2出口温度升高，热回收量、制热COP和COP降低，并缩小了循环进行热回收运行的压力范围。当第二级质量流量比为1.2时，对应于最大综合COP的排气压力由10.2 MPa移至10.9 MPa，最大综合COP由3.538降至3.496。

3.2 第一级质量流量比渐变

图10所示为CO2出口温度的变化情况。可知，第一级质量流量比越大，温度滑移匹配越好，CO2出口温度越低。当第一级质量流量比较小时，CO2出口温度随排气压力的升高而增大。原因是第一级热回收温度滑移匹配较差，第一级热回收的夹点基本均出现在最右端，而随着排气压力的升高，CO2换热曲线在T-Q图上整体均上移，使CO2出口温度也随之升高。

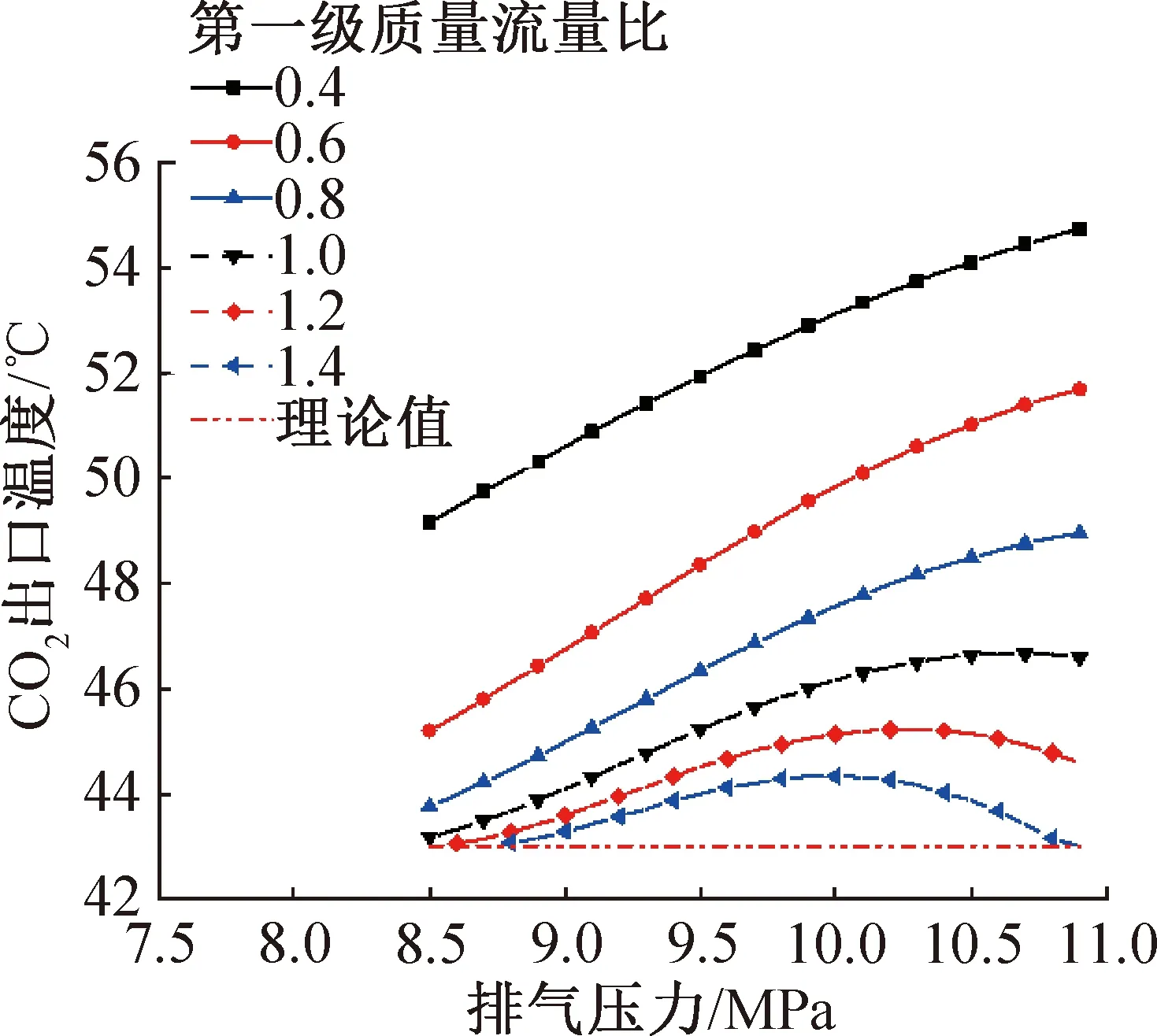
图10 不同第一级质量流量比下CO2出口温度随排气压力的变化Fig.10 Variation of CO2 outlet temperature with discharge pressure under different first stage mass flow ratio

当质量流量比升高后，CO2出口温度随排气压力的升高先增大后减小。原因是此时低温级整体的温度滑移匹配较好（整体传热温差较小），第一级热回收的夹点位置受排气压力的影响，在低排气压力时，近临界点温度较低，此时夹点出现在低温级热回收最左端，故此时CO2出口温度达到最小值，而随着排气压力升高，近临界点温度升高，夹点向第一级的中间移动，使CO2出口温度升高，排气压力继续升高，此时低温级换热区域又开始逐渐横跨CO2换热曲线的近临界点左右侧，使夹点同时出现在低温级热回收的左右侧，CO2出口温度又开始降低，直至理论值。

综上所述，不同的质量流量比会影响CO2出口温度随排气压力的变化趋势,质量流量比越大，整体CO2出口温度变小。

图11所示为相应第二级质量流量比的变化情况。第二级质量流量比随排气压力的升高和第一级质量流量比的降低而升高。对应图10可知，若需降低CO2出口温度，则需降低排气压力，升高第一级质量流量比，降低第二级质量流量比。

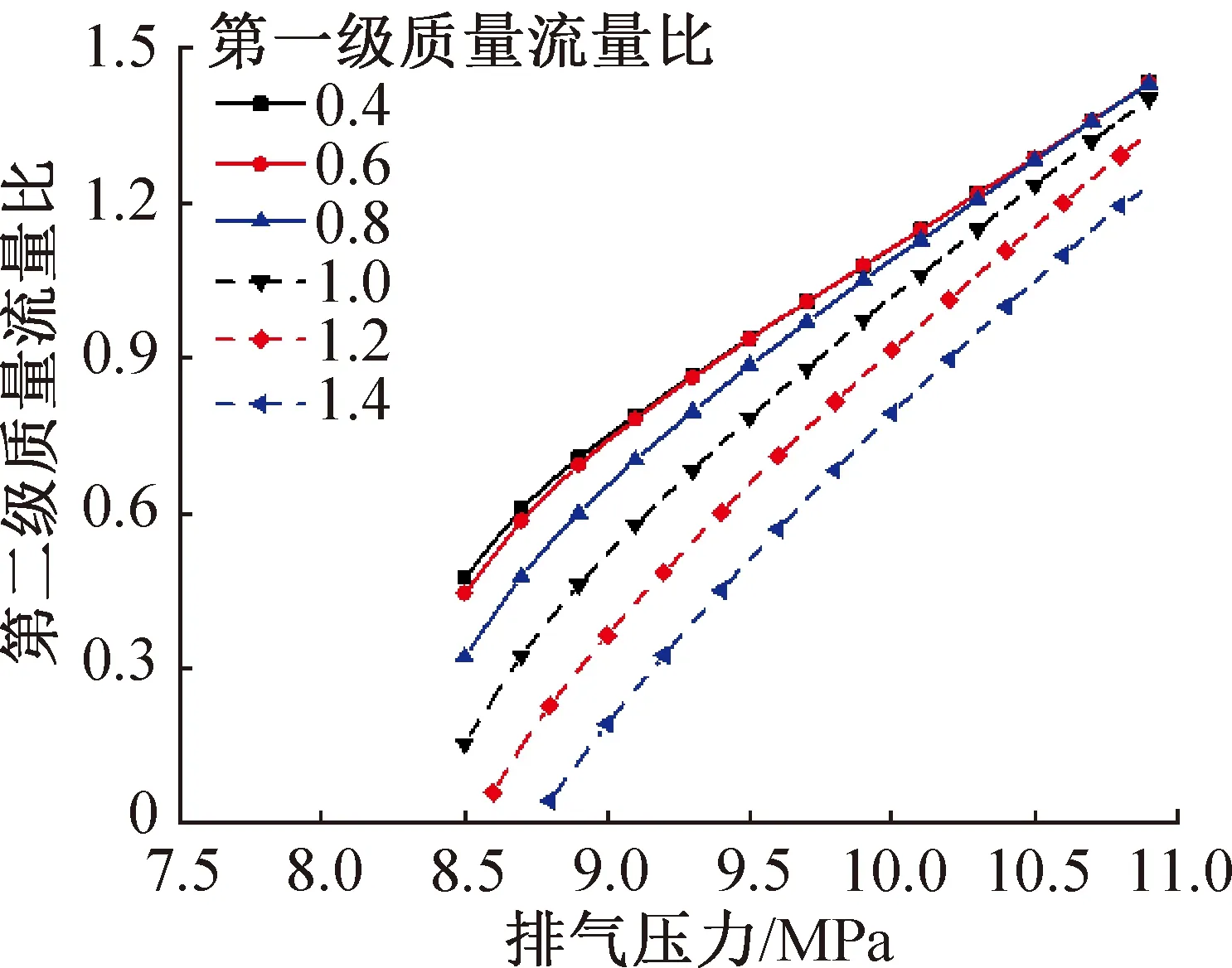
图11 不同第一级质量流量比下第二级质量流量比随排气压力的变化Fig.11 Variation of second stage mass flow ratio with discharge pressure under different first stage mass flow ratio

图12所示为热回收量的变化情况。与理论情况下CO2出口温度不随排气压力变化不同，当质量流量较小时，CO2出口温度会随排气压力的升高而升高，导致热回收的单位焓差变小，热回收量在理论值的基础上有所降低，因此在后半段，低质量流量比下的升高趋势明显变缓，而高质量流量比下因CO2出口温度降低，使变化趋势反而变陡。

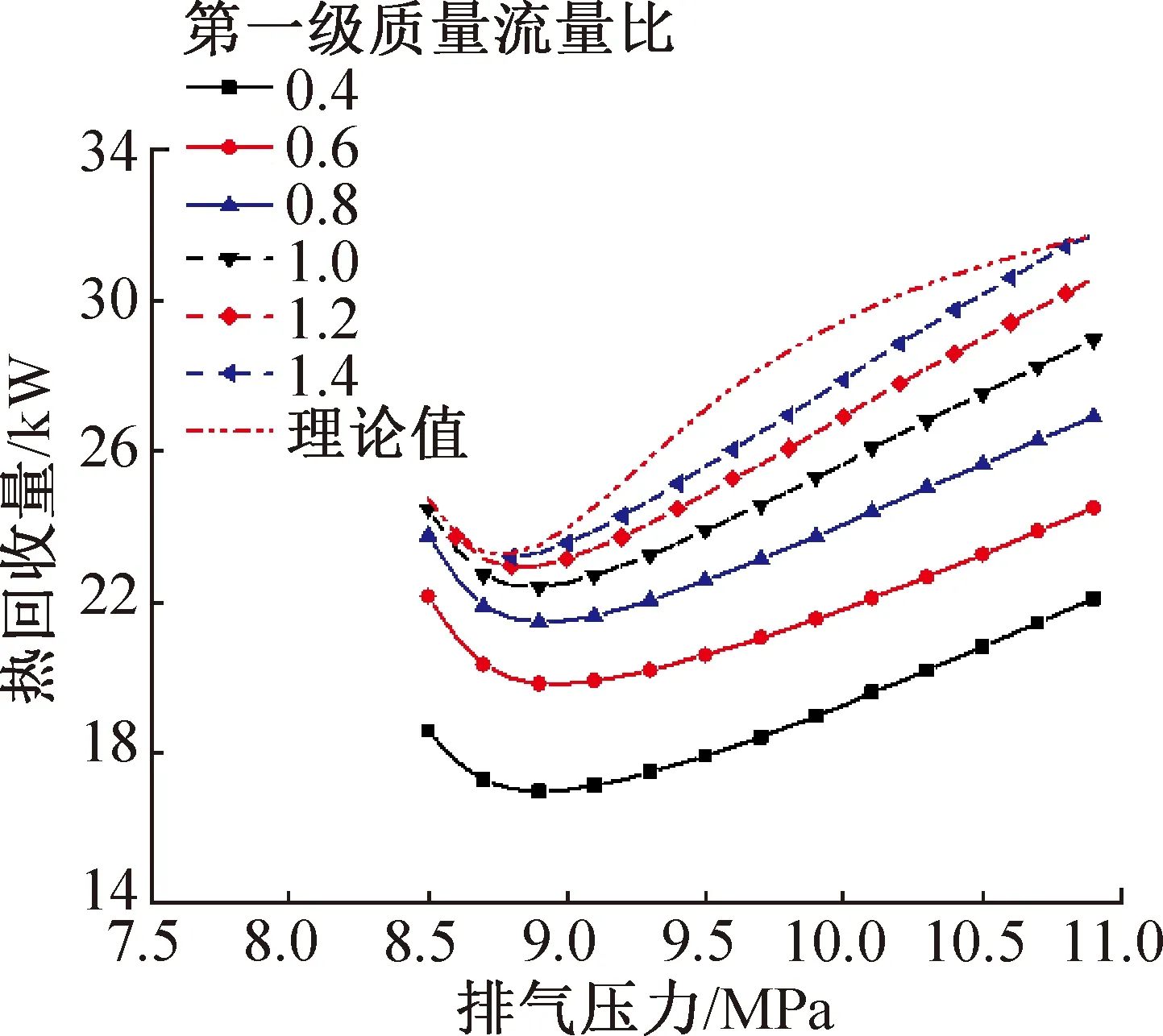
图12 不同第一级质量流量比下热回收量随排气压力的变化Fig.12 Variation of heat recovery with discharge pressure under different first stage mass flow ratio

前半段趋势基本没变化主要原因是此时质量流量相对较大，单位焓差变化的影响较小。总体而言，质量流量比越大，热回收量越大。

图13所示为不同第一级质量流量比下，制热性能系数随排气压力变化。可以看出，前半段升高趋势变缓，后半段升高趋势因质量流量比的不同而变化，与前文分析一致。

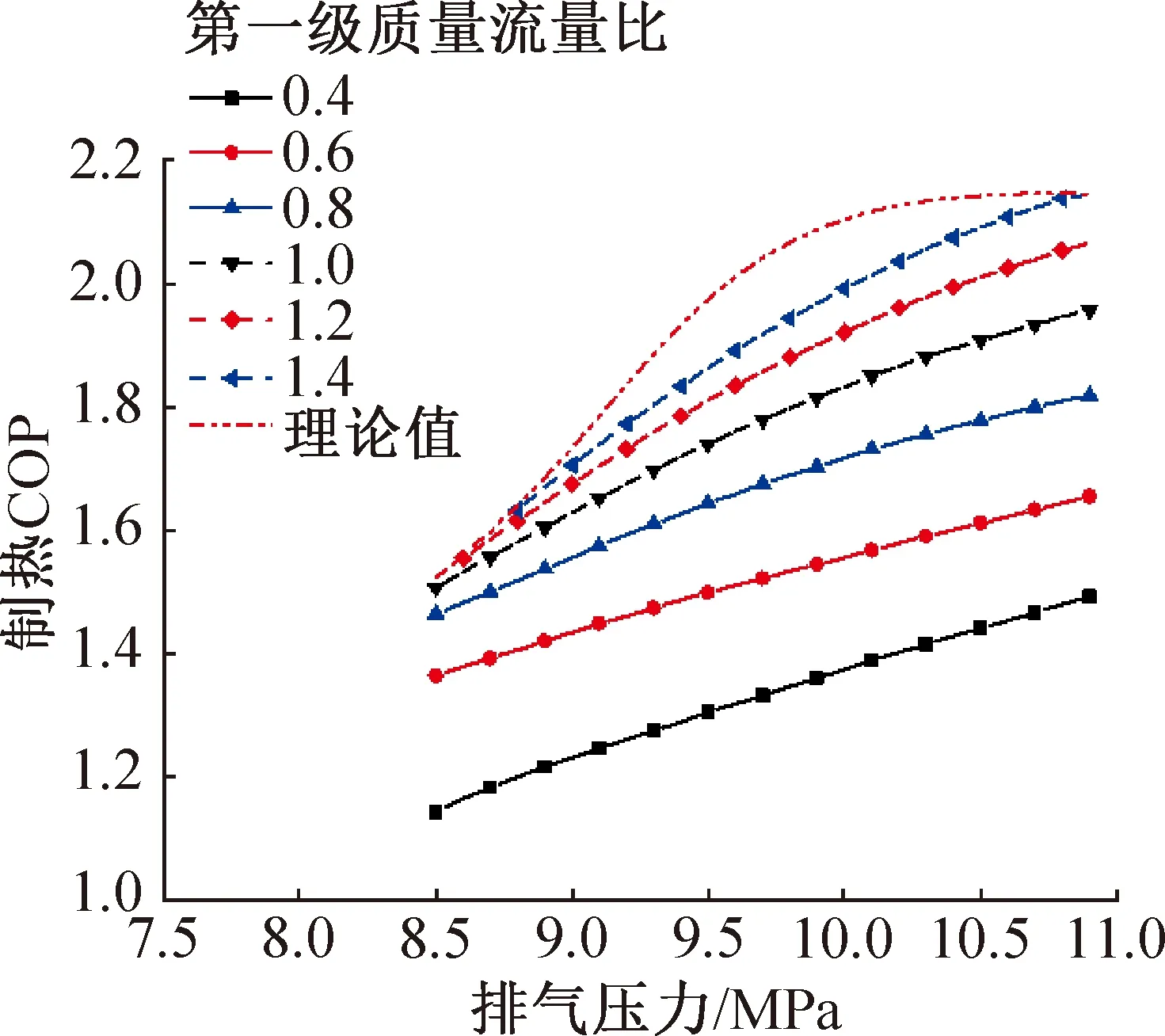
图13 不同第一级质量流量比下制热COP随排气压力的变化Fig.13 Variation of heat coefficient of performance with discharge pressure under different first stage mass flow ratio

图14所示为不同第一级质量流量比下，COP随排气压力的变化。质量流量比越大，COP越大；此时由于最佳排气压力后移超过排气压力上限值，故所有质量流量比下均为排气压力10.9 MPa时的综合COP最大，当第一级质量流量比为1.4时，最大综合COP降至3.496，而当第一级质量流量比为0.4时，最大综合COP仅为2.843。

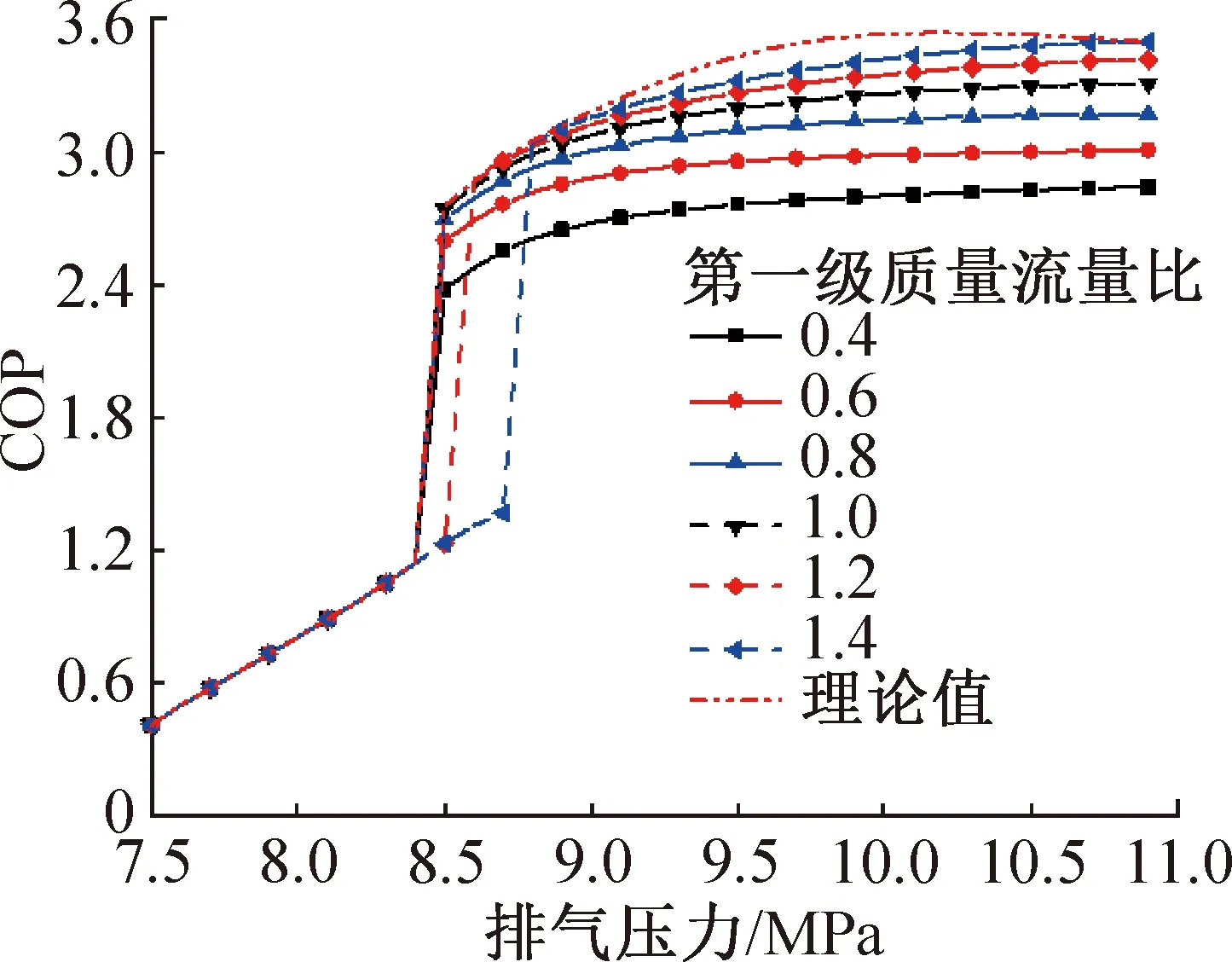
图14 不同第一级质量流量比下综合COP随排气压力的变化Fig.14 Variation of comprehensive coefficient of performance with discharge pressure under different first stage mass flow ratio

由上述分析可知，当第一级质量流量比渐变第二级相应调节时，第一级质量流量比越大越好，同时升高排气压力和第二级质量流量比来降低CO2出口温度，提升系统性能。

4 结论

本文基于人工冰场CO2制冷及热回收系统，采用夹点分析法对双级热回收设计进行热力学优化分析，得到如下结论：

1）当第二级质量流量比在0.4～1.4之间渐变，相应调节第一级质量流量比来降低CO2出口温度时，发现应降低第二级质量流量比，升高排气压力，有效降低CO2出口温度；当第二级质量流量比为0.4时，系统性能和理论保持一致，为1.4时，最大综合COP由3.538降至3.496，同时最佳排气压力由10.2 MPa升至10.9 MPa。

2）当第一级质量流量比在0.4～1.2之间渐变，相应调节第二级质量流量比来降低CO2出口温度时，应升高第一级质量流量比，同时升高排气压力；此时最佳排气压力总为10.9 MPa，且当第一级质量流量比为0.4时，最大综合COP仅为2.843。

3）总体而言，应降低第二级质量流量比，提高第一级质量流量比，提高排气压力，从而提升系统综合性能。

符号说明

m——质量流量，kg/s

h——制冷剂焓值，kJ/kg

p——制冷剂压力，MPa

T——温度，℃

W——压缩机功耗，kW

Q——制热（冷）量，kW

下标

1、2……12——相应状态点

c——蒸发器流向压缩机的流体

e——蒸发器流向喷射器的流体

in——压缩机进口

out——压缩机出口

com——压缩机

r——制冷

hr——热回收