基于改进动态时间弯曲距离算法的直流配电网线路纵联保护方案

冉启胜，张 哲，韩杰祥，尹项根，热合曼·玉山，刘玢岩

（华中科技大学 强电磁工程与新技术国家重点实验室，湖北 武汉 430074）

0 引言

直流配电网是一个低惯量、弱阻尼系统，当线路发生极间故障时，若不及时投入故障控制或隔离故障区域，交直流系统短时间内将会出现严重过流［1-2］，进而威胁系统运行安全。基于故障阻断型换流器的直流配电网具备主动限流能力，故障后可通过限流控制主动降低系统的故障电流水平，从而减少对交直流电网的短路冲击，降低对开关设备和保护的动作速度要求，已成为直流配电网的主要发展方向［3］。然而，主动限流控制将导致故障电流特性复杂化，故障特征减弱，给继电保护带来诸多不利影响［4］，因此需要有针对性地开展保护新原理研究，以保证直流配电网的运行安全。

目前，直流配电网线路保护研究大多没有计及主动限流控制的影响。文献［5-7］根据线路两侧限流电抗器的电压变化率、电压初始值以及电压积分值进行故障判断。这些保护原理均需要依靠边界元件来区分故障线路，当配电网采用主动限流控制后，线路两端无需装设电抗器，将导致这些保护原理失效［8］。文献［9］根据故障初期电流快速上升的特点，利用电流的幅值和正负构造方向纵联保护，但该方法利用的故障信息有限，影响其可靠性，也无法适应单侧电源供电的应用场合。

对于主动限流型直流配电网，其线路保护的研究尚处于起步阶段［3］。纵联电流差动保护在原理上具有绝对的选择性，但要求线路两侧数据采样严格同步，在配电网中应用受到局限［8］。此外，主动限流控制后线路故障电流水平较低，导致保护灵敏度严重下降。文献［10］提出一种检测两侧电流是否同步过零的纵联保护方案，但是该保护方案受分布电容电流影响较大，特别是线路接近空载时，电流可能会受分布电容电流振荡特性的影响反复出现过零点，导致保护误动或拒动。文献［11］考虑主动限流控制的作用，提出了一种基于电流极性比较的纵联保护原理，能够准确区分区内、外故障，但是该原理应用于单侧电源供电线路时，由于无电源侧故障电流极性不明确，可能导致保护失效。

本文以典型的中压直流配电网为例，分析了发生极间故障时，主动限流控制作用下故障电流的变化特性。在此基础上，提出了一种基于改进动态时间弯曲距离DTW（Dynamic Time Warping distance）算法的线路纵联保护方案：通过欧氏距离度量的方法比较限流前后线路两侧故障电流波形的相似性区分区内、外故障，以提高保护的可靠性和适用性；采用故障起始时刻的自校正以及优化DTW 加权函数的方法消除采样同步误差的影响。仿真算例验证了所提保护方案的良好性能。

1 柔性中压直流配电网结构

主动限流型直流配电网主要通过是具有主动限流控制能力的全桥-半桥模块化多电平换流器FH-MMC（Full bridge and Half bridge-Modular Multilevel Converter）与交流电网互联，交直流负荷和交直流微电网均通过拥有故障隔离功能的DC／AC、DC／DC变换环节接入直流母线。附录A图A1给出了双端中压直流配电网典型拓扑示例，直流线路L1—L3两侧均配置遮断容量要求和速度要求较低的直流断路器DCCB（Direct Current Circuit Breaker），用于隔离故障线路、提高故障恢复速度。由于采用限流控制，配电网各段线路两侧一般不装设限流电抗器，仅在FH-MMC 出口配置容量较小的限流电抗器，与桥臂电抗一起限制故障电流的上升速率。为满足不同位置负荷、分布式电源接入的要求，直流配电网呈现多分段的特点。配电系统交流侧各换流变均采用△／Y 联结方式，并在Y 侧经大电阻接地，以限制单极接地故障下的入地电流幅值，保证故障点附近人员和设备的安全［12］。对于上述小电流接地直流配电系统，只有当发生双极故障时，才会产生较大的故障电流，需要进行限流控制，并快速隔离故障。本文将重点针对双极故障电流特性和保护原理开展研究。

2 主动限流控制及故障特性分析

保护以故障特征为基础，主动限流后故障特性将复杂化，进而对保护造成较大的影响。本节计及主动限流控制的影响，分析线路电流故障特性，为后续保护原理研究提供理论依据。

2.1 主动限流控制

具有主动限流控制能力的FH-MMC典型拓扑结构如附录A 图A2所示，适用于该拓扑的主动限流控制策略见附录A 图A3。正常运行期间，有功类控制外环选择模式0 或模式1 进行定有功功率或定直流电压控制，无功类控制外环采用定无功功率控制，内环交流电流控制采用传统的前馈解耦控制策略，传统的二倍频环流抑制控制始终处于投入状态，上下桥臂参考电压的直流偏置量Udcref/2通过正常控制生成。发生极间故障后，换流站控制器依据预设的启动判据切换至主动限流控制，有功类控制外环选择模式2 进行子模块电容电压控制，同时引入直流电流反馈控制［13］。

故障穿越期间子模块投切控制如附录A 图A4所示。图中：x为相别，x=a，b，c；u 和l 分别表示上桥臂和下桥臂。由于故障期间桥臂电流恒为正值，半桥子模块电容电压无法平衡，因此将所有半桥子模块旁路，仅利用全桥子模块进行故障阻断和限流控制［2，13］。子模块的调制波由电流内环分量mx、直流分量Udcref/2、环流抑制分量mcirx和电容电压均衡控制分量四部分组成，然后与上下层叠的三角载波对比产生子模块脉冲控制信号。直流电流反馈控制调节调制波的直流分量Udcref/2，使换流器端口输出直流电压能够自动调整以适应直流电流指令值。因此，理论上线路上的故障电流可以被限制在安全范围内的任意值。

故障后主动限流控制的启动方式决定了各换流站控制策略的切换时刻，控制目标决定了故障后稳态电流的大小，是影响故障电流变化特性的2 个主要因素。

为了确保换流站不因过流而闭锁，主动限流控制可使用过电流启动策略［11］。该启动策略的实施思路为：当换流站控制器监测端口的直流电流达到额定值的2 倍时，控制策略切换至主动限流控制。各换流站控制器过电流启动判据如式（1）所示。

式中：idc为直流电流瞬时值；IdcN为直流电流额定值。

主动限流控制目标决定了故障后稳态电流幅值，对该值的选取需考虑诸多因素。一方面，为降低故障电流的影响，控制目标设置得越低越好；另一方面，若将控制目标设置为0，则电流故障特性消失，不利于故障线路的辨识，同时，也难以判断故障支路是否被隔离，从而影响换流器的恢复速度。综合考虑以上2 个方面的需求，可以设置主动限流指令值Idcref=0.4 p.u.。

2.2 故障特性分析

采用主动限流控制时，可将配电网线路双极故障的演变过程划分为限流前和限流后2 个阶段：第一阶段为换流站子模块电容向故障点放电，即限流前故障自然演进阶段；第二阶段为主动限流控制生效后，故障电流受直流电流反馈控制调节，下文称之为电流受控阶段。在控制策略切换时，虽然存在暂态过程，但由于其持续时间较短，在故障发展全过程中占比较小，可近似忽略其影响。

为使整个中压直流配电网具有故障阻断的能力，直流母线接出的负荷一般采用开关电容型换流器作为接口［14-15］。检测到极间故障后，负荷接口处的换流器会迅速闭锁，从而切断与直流母线的联系，因此负荷不会向故障点馈入很大的故障电流，且持续时间较短（只是存在于故障检测的时间内），可忽略不计。此外，双极故障一般为金属性故障，过渡电阻很小，各FH-MMC 到故障点形成的馈流回路可近似认为是解耦的，可单独分析。

以线路L1末端点f1发生金属性双极故障为例，对其故障电流特性进行分析，其他位置故障的分析过程类似，本文不再赘述。FH-MMC、线路和过渡电阻构成的等效故障回路如图1 所示。图中：C0、L0和R0分别为单个子模块电容、桥臂电感和桥臂等效电阻；N为每个桥臂子模块额定数目；Lc为限流电感；Rd和Ld分别为线路L1的电阻和电感。

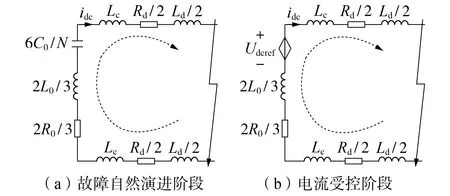
图1 等效故障回路Fig.1 Equivalent fault circuit

图1（a）为故障自然演进阶段的等效故障回路示意图，该阶段主要是子模块电容向故障点放电形成故障电流，端口电流的时域解析式如式（2）所示。

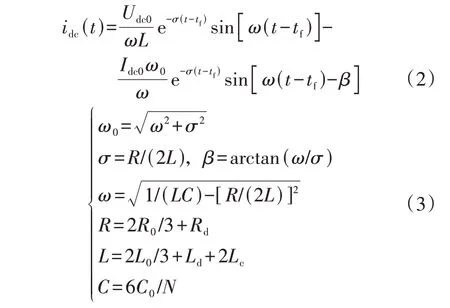
式中：tf为故障发生时刻；Udc0和Idc0分别为极间电压和直流电流初值。

图1（b）为电流受控阶段等效故障回路示意图，在主动限流控制的作用下，子模块电容可等效为1个受直流电流反馈控制调节的直流电压源，根据图A3 可知其幅值为Udcref。容易看出，该阶段等效故障回路为一阶RL电路，端口电流时域解析式为［11］：

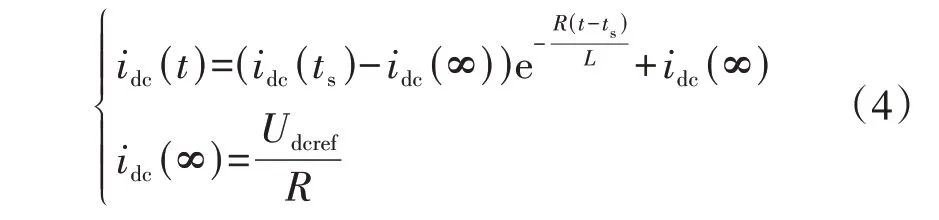
式中：ts为主动限流控制生效时刻；idc(ts)可由式（2）得到；idc(∞)即为给定的直流电流指令值Idcref。

式（2）、（4）给出了计及主动限流控制的故障发展全过程电流的解析表达式。在故障自然演进阶段电流表征为集中电容放电，其幅值迅速上升，在式（1）所示的过电流启动判据下，持续时间较短；在电流受控阶段，电流表征为一阶惯性下降，由于故障回路等效时间常数较小，故障电流表现为快速下降，然后稳定在指定的直流电流大小附近。计及主动限流控制的故障全过程线路电流如附录A图A5所示。

以图A1 所示的直流配电网为例，附录A 图A6给出了不同位置发生故障时线路L1的M1侧电流i12的变化特性。图中：仿真结果均为标幺值，后同；f1—f3分别表示L1末端短路、L2中点短路、L3中点短路故障点。可以看出，电流的峰值基本不随故障位置的变化而变化，只是到达峰值的时间和进入故障后稳态的时间稍有差别，即故障电流波形特征受故障位置的影响较小。

图2和图3以线路L2为例，分别给出了线路发生区外（点f1）故障和区内（点f2）故障下，线路L2两侧电流i23和i32以及-i32的波形，规定电流的正方向均由母线指向线路。可以看出：发生区外故障时，故障电流具备穿越性质，线路本侧正方向电流和对侧反方向电流几乎重合，相似度很高；而发生区内故障时，故障电流不具备穿越性质，线路本侧正方向电流和对侧反方向电流具有很大差异，且在主动限流控制作用下，即使故障进入稳态，该差异依然存在。

图2 区外故障下电流波形Fig.2 Current waveforms under external fault

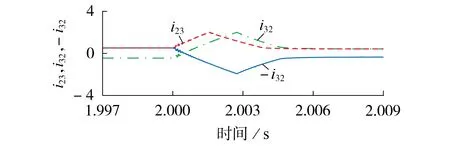
图3 区内故障下电流波形Fig.3 Current waveforms under internal fault

此外，直流配电系统有多种运行方式，例如单换流器运行、双端隔离运行等方式［16］，则线路可能处于单侧供电状态。例如图A1 中FH-MMC1退出运行时，所有线路均处于单侧供电状态。在该运行工况下，线路无电源侧仅有接入的负荷为其提供故障电流，然而故障阻断型DC／AC 和DC／DC 变换器在检测到极间故障后将闭锁［3］，提供的故障电流非常有限，如附录A 图A7 所示。故障发生后，线路无源侧电流快速衰减到0，初始阶段的振荡为线路分布电容电流。

根据以上对故障电流的理论分析，可以得到以下基本结论。

1）采用主动限流控制后，故障电流变化可划分为限流前和限流后2 个阶段，限流前故障电流快速上升，限流后故障电流快速下降并稳定在指令值附近。

2）限流前故障电流暂态过程主要受限流启动判据影响，持续时间较短，单纯利用限流前故障暂态信息会影响保护可靠性。综合利用故障全过程电流信息有助于提高保护可靠性，同时可降低对采样率的要求，降低设备成本。

3）主动限流后，故障电流水平受故障点位置影响较小。单侧电源供电时，线路无电源侧电流快速衰减到0，故障特征不足。另外，线路上没有配置限流电抗器等边界元件，这些因素导致单侧量保护难以应用，需综合利用两侧电流信息进行故障判断。

4）无论是限流前还是限流后，发生区外故障时线路本侧正方向和对侧反方向电流波形基本相同，发生区内故障时则存在较大差异。上述特点在故障暂态和稳态过程中持续存在，且不受双电源供电还是单电源供电的影响。

综上所述，对于主动限流型直流配电网，由于故障特性复杂，且受换流器运行方式的影响，单侧量保护难以应用。综合利用限流前后故障电流全过程变化特征，特别是线路两侧电流波形的相似度特征，可有效识别区内、外故障，提高保护的可靠性和适用性。同时，无线通信技术的快速发展，特别是5G 技术日益成熟，可为配电网纵联保护的工程应用提供有力的技术支持。

3 基于改进DTW算法的纵联保护原理

前文的分析表明，对于主动限流型直流配电网，可以通过比较线路两侧电流波形的相似度构造纵联保护判据。DTW 算法运用动态规划技术，将2 个序列进行柔性匹配，通过计算欧氏距离实现两序列相似性的度量。在应用于配电网保护时，由于线路两侧采样同步困难，在算法设计时，需要重点解决采样不同步给距离（波形）相似度比较带来的误差问题，以保证保护动作的正确性。

3.1 DTW算法的基本原理

DTW 算法通过将时间轴进行拉伸，对2 个时间序列进行局部的扩展，调整其相应元素的对应关系并进行对齐，最终搜索得出一条最优的弯曲路径，该路径下两序列间的欧氏距离最小。因此，DTW 将两时间序列进行最优匹配后输出的欧氏距离体现了序列间的相似程度，欧氏距离越小则两序列相似度越高［17］。

DTW 算法搜索两序列最优弯曲路径的过程如图4 所示。设有2 个长度分别为n和m的时间序列P=｛p1，p2，…，pj，…，pn｝和Q=｛q1，q2，…，qi，…，qm｝，首先形成序列间的代价矩阵，矩阵元素为两序列对应下标元素之间的欧氏距离，如式（5）所示。

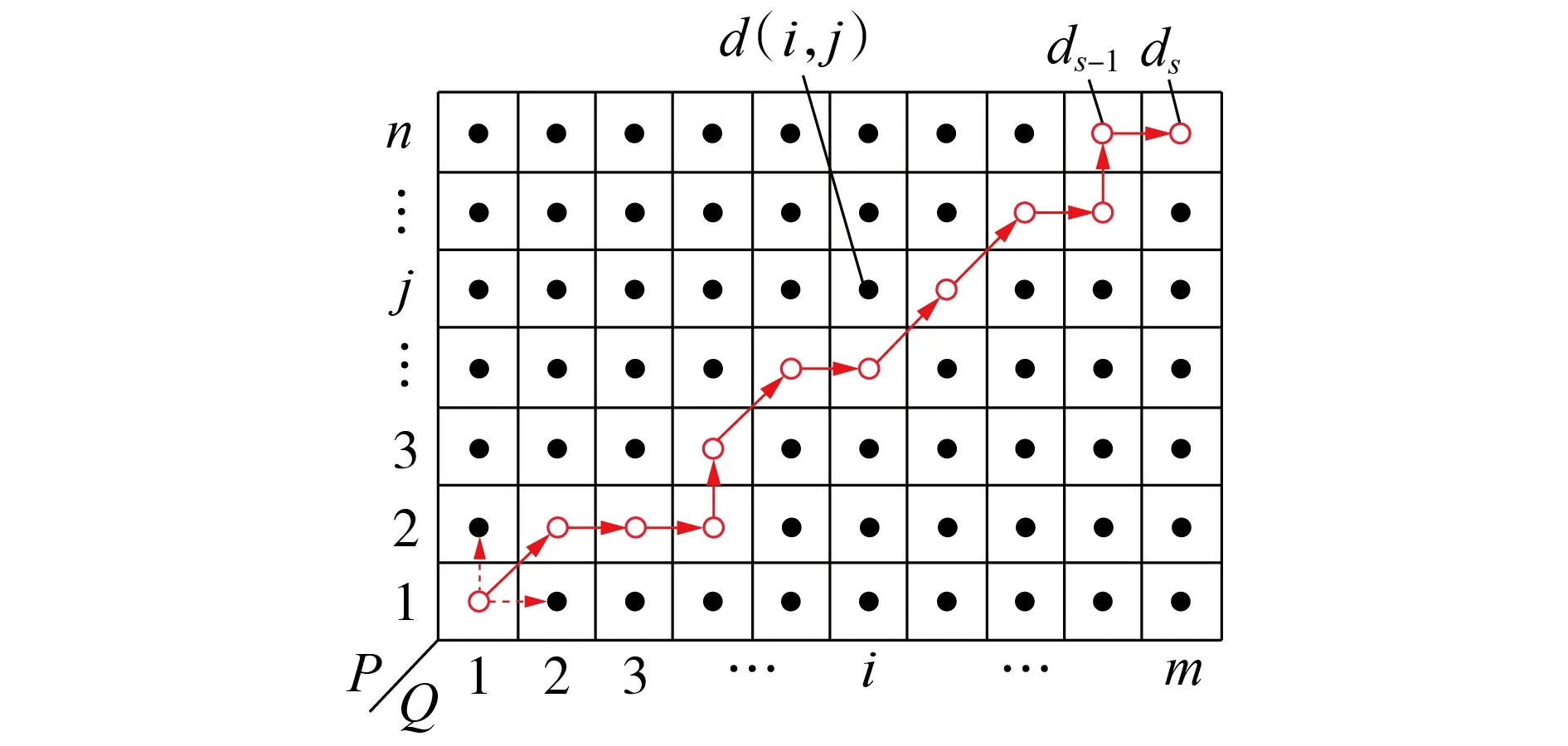
图4 最优弯曲路径搜索过程Fig.4 Searching process of optimal warping path

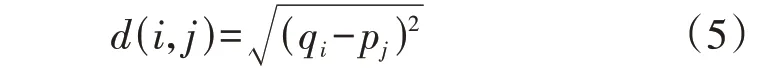
DTW算法对搜索路径有如下约束。

1）边界约束。起点为d（1，1），终点为d（m，n），该约束条件将搜索路径的起点和终点固定在两时间序列的首端和末端。

2）弯曲路径连续且单调不减约束。在搜索过程中行指标和列指标都是单调不减的，如图4 中起点d（1，1）处箭头标出的允许搜索方向所示，其中实线箭头对应实际最优路径的搜索方向。

满足上述约束条件的路径有很多条，将其组成一个路径集合G，DTW 算法即为寻找一条最佳的规整路径G*，使该路径所经过的代价矩阵中各元素的累积之和最小。按照先后顺序记G*中各元素分别为G*=｛d1，d2，…，ds｝，其中s为最优路径的长度且max（m，n）≤s≤m+n。图4 中代价矩阵内的空心圆点即为最佳规整路径上的各元素集合，下文将其称为每一步欧氏距离dk（累积距离由每一步欧氏距离求和得出）。则最终输出的两时间序列间动态时间弯曲距离dDTW(P，Q)为：

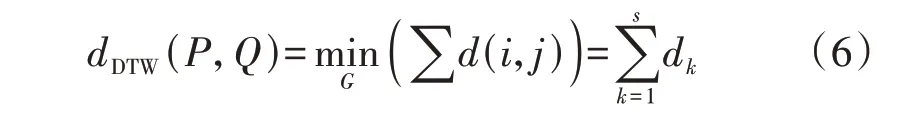
采用DTW 算法进行线路两侧波形相似度比较时，可利用线路两侧故障启动元件（下文将进行具体说明）的启动时刻作为两侧数据同步的初始校正，即参与波形相似度比较的电流采样数据均以本侧启动元件的动作时刻作为波形比较数据的起点。因此，两侧波形比较的同步误差包括两侧启动元件动作不一致带来的同步误差（下文简称启动同步误差），以及两侧保护装置采样时钟不严格同步带来的同步误差（下文简称时钟同步误差）。由于直流线路保护采样频率一般较高，采样间隔较小，而时钟同步误差不大于1 个采样周期，因此两侧波形的相似程度受时钟同步误差的影响相对较小，可在阈值整定计算时予以考虑。启动同步误差可能达到多个采样间隔，会在较大程度上减弱区外故障下两侧电流波形的相似性，从而使欧氏距离异常增大，需要采取措施降低其影响。

3.2 改进DTW算法

为了便于说明，以图2 所示的区外故障线路两侧电流波形的故障分量为例，假设存在10 个采样间隔的启动同步误差。两侧电流原始采样数据序列经过DTW 算法处理后的对齐信号如附录A 图A8 所示。对齐信号中两序列各点对应的欧氏距离即为每一步欧氏距离dk。由图A8（b）可以看出，经过局部扭曲和扩展后，两序列在中间的绝大部分实现了对齐，仅在首端和末端出现较大的局部欧氏距离，即边缘效应。

首、末端出现的边缘效应主要是由于两侧启动元件动作不一致产生，其值较大时，DTW 算法的输出值会异常增加，导致序列间相似性减弱，影响保护动作性能。为解决该问题，一种可行方案是对每一步欧氏距离进行加权，形成加权动态时间弯曲距离WDTW（Weighted Dynamic Time Warping distance）dWDTW(P，Q)，如式（7）所示。

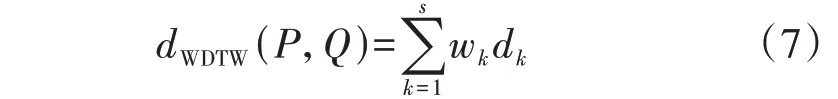
式中：wk为权函数。通过改进权函数的分布优化DTW算法的输出值，从而降低边缘效应的影响。

由图A8（b）可见，越靠近序列首端和末端其局部欧氏距离越大，而中间部分实现了对齐，局部欧氏距离接近于0，因此可适当减小序列首端和末端的加权系数以抑制边缘效应影响。可构造如下加权函数：

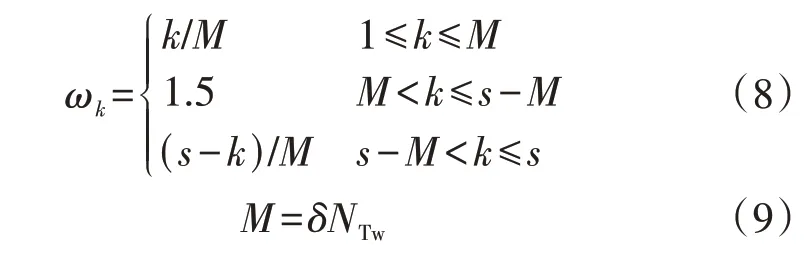
式中：δ为最大同步误差占计算数据窗百分比；NTw为1个计算数据窗内的采样点数。

式（8）所示的加权函数将对齐信号前M项加权系数按照递增的规律增加到1，在中间部分保持为1.5不变，将后M项加权系数按照递减规律减小到0。M可根据两侧序列可能出现的最大同步误差进行整定，如式（9）所示。上述方法通过减小序列首端和末端的加权系数抑制边缘效应，可有效增强算法耐受同步误差的能力。另一方面，加大中间部分的加权系数能够进一步增强区内、外故障波形之间的差异，从而提高保护的可靠性和灵敏性。

3.3 纵联保护方案

3.3.1 保护启动判据

故障后线路两侧极间电压跌落特征快速而明显，因此可利用电压梯度算法［18］检测极间故障，其定义为：

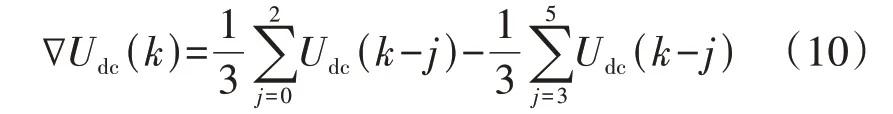
式中：Udc(k)为极间电压当前采样值；∇Udc(k)为当前电压梯度计算值。

该梯度算法具有较高的灵敏度，能够较为准确地检测故障发生时刻，将故障后两侧启动同步误差限定在可接受范围内。

保护的启动判据为：

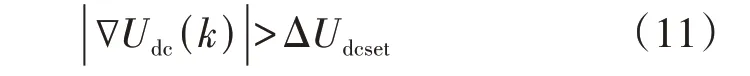
式中：ΔUdcset为保护启动阈值，可按照耐受最大过渡电阻能力整定。

3.3.2 保护主判据

为了消除故障电流负荷分量的影响，利用线路两侧电流故障分量通过WDTW 算法衡量其相似程度，进而实现故障判断。以保护启动判据动作时刻为起点，向后取1 个计算窗数据进行故障判断。假设线路本侧电流故障分量为Δi1，对侧传递过来的电流故障分量为Δi2，则保护动作判据为：

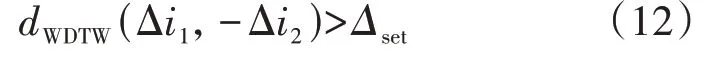
式中：Δset为保护动作阈值，其应能够有效防止发生区外故障时由于同步误差造成保护误动，可按躲过启动同步误差和时钟同步误差同时存在时WDTW的最大值整定。

上述判据在故障启动后一直投入，以综合利用限流前后的故障电流全过程变化特征。保护方案流程图如附录A 图A9 所示，为提高保护可靠性，在计算数据窗滑动的过程中，保护判据连续成立Nr次才判断为区内故障，Nr根据保护可靠性要求进行整定，可设置为3。

4 算例分析

为验证本文所提纵联保护方案的正确性和适用性，在PSCAD／EMTDC 仿真平台搭建了图A1 所示的仿真模型，模型参数设置如附录A 表A1所示，2个FH-MMC 参数一致。正常运行时FH-MMC1为定功率控制，向外传输10 MW 有功；FH-MMC2为定直流电压控制，处于逆变状态。

纵联保护采样频率为10 kHz，综合考虑保护的可靠性要求和速动性要求，将计算数据窗长设置为5 ms，该数据窗包含的采样点数NTw=50。保护在计算数据窗的滑动过程中舍弃开始的1 ms 数据并向后更新1 ms 数据，进行下一次判断，因此保护判据连续满足3 次，即识别故障的时间为7 ms。研究表明，中压直流配电网发生极间故障时过渡电阻一般不超过20 Ω［19］，可按照耐受最大过渡电阻能力整定ΔUdcset=0.1UdcN=2 kV，其中UdcN为直流电压额定值。保护动作量Δset按躲过启动同步误差和时钟同步误差同时存在时WDTW 的最大值整定，其中启动同步误差按较为严苛的1 ms 考虑。仿真实验表明，发生区外故障时，若同时计及启动同步误差和时钟同步误差的影响，则WDTW 算法的输出最大距离不超过5 p.u.。取可靠系数为2，则保护动作阈值Δset整定为10 p.u.。发生区内故障时，对保护最不利的情况为单侧电源短路故障，故障稳态后在主动限流控制的作用下保护动作量近似为1.5IdcrefNTw=1.5×0.4×50=30 p.u.，此时保护的灵敏系数为3，满足保护的灵敏性要求。

4.1 保护区内外故障辨识能力验证

以线路L2上的纵联保护为例，分别设置金属性区外故障FL1j和FL3j以及区内故障FL2j，其中j取b、m、e 时分别表示线路首端、中点和末端故障，不同故障位置下纵联保护的判断结果如附录A 表A2所示。表中：保护动作量均为标幺值，后同；针对区外故障和区内故障分别给出的是Nr次判断中保护动作量的最大值和最小值。由表可见，发生区内故障时，本文所提改进DTW 算法的动作量远大于门槛值10 p.u.，而在发生区外故障时，该算法的动作量远小于门槛值，因此本文所提改进DTW 算法能够准确可靠地区分区内、外故障。

4.2 同步误差对保护性能影响的仿真分析

由于线路两侧装置采样率相同，故时钟同步误差不大于1 个采样间隔Ts。而本文采用的算法有类似平移对齐的功能，因此，在时钟同步误差为-Ts/2或Ts/2 时两侧电流相似程度最低，对保护的影响最大。在两侧电流数据中分别设置1 ms 的启动同步误差、Ts/2的时钟同步误差以及2种误差混合的同步误差，对保护动作性能进行仿真分析，线路L2上纵联保护的判断结果如附录A 表A3 所示。结合表A2、A3 分析可知，时钟同步误差和启动同步误差均会导致区外故障下的保护动作量增大，但后者起主导作用，与理论分析结论一致。通过表A3 还可以看出，即使2 种同步误差同时存在，区外故障下的保护动作量仍小于整定阈值，保护不会误动作。

为了进一步验证本文所提改进DTW 算法的性能，针对不同的启动同步误差情况，对比分析了本文算法与传统DTW 算法的抗同步误差的能力，结果见附录A 图A10。可以看出，在区外故障下，随着同步误差的增大，基于传统DTW 算法构造的保护动作量显著增加，在同步误差达到±1 ms 时接近整定阈值，保护有误动的危险。而基于改进DTW 算法的保护判据表现良好，动作量受同步误差的影响较小，抗同步误差的能力远优于传统算法。

4.3 保护耐受过渡电阻能力

过渡电阻较大时，对于区外故障，故障电流仍然具备穿越性质，保护动作量仍接近于0，保护能够可靠地不动作。而发生区内故障时，故障线路两侧的电流波形差异变化较为明显，影响保护动作性能。因此，需着重分析区内各个位置经不同过渡电阻发生故障时，保护的动作情况。在仿真中设置线路L2首端、中点和末端分别经0、5、10、20 Ω 过渡电阻的极间故障，保护的动作情况如附录A 表A4所示。可以看出，随着过渡电阻的增大，保护动作量略有增加，有利于保护可靠动作。其原因在于，过渡电阻增加后故障电流进入稳态的时间变长，保护能够利用的暂态数据增多，而暂态电流在数值上要大于稳态电流，使得保护动作量增加，因此所提方法具有较好的耐受过渡电阻能力。

4.4 单侧电源供电时保护性能验证

针对附录A 图A1 所示的双端直流配电网，对保护最不利的情况是单侧电源运行状态。假设只有定直流电压站FH-MMC2处于运行状态，验证本文所提保护方案的适用性，并与文献［11］提出的基于极性信息的斯皮尔曼相似性保护原理（若斯皮尔曼相关系数大于0.5则判断为区内故障）进行对比分析。

单侧电源供电时线路L2中点发生极间故障时，两侧保护测得的电流波形见附录A 图A11。可以看出，由于无源侧电流为电容电流，经振荡后会稳定在0。振荡电流和零流会导致基于极性信息的斯皮尔曼相似性判断方法误判，进而造成保护拒动（见附录A表A5）。而本文提出的改进DTW算法综合利用了两侧电流的极性和幅值特征，在上述故障情况下，由于两侧电流在幅值上存在较大差异，计算得到的WDTW 值将会超过动作阈值，可保证保护灵敏可靠动作。不同故障情况下，本文所提保护原理和基于斯皮尔曼相似性的保护原理的仿真结果如附录A 表A5 所示。结果表明，本文所提保护原理对单侧电源供电线路具有良好的适应性，其性能明显优于基于极性信息的相似度比较方法。

4.5 保护耐受分布电容电流能力

在4.4节的基础上，考虑对保护最不利的单侧电源经高阻短路故障工况，将分布电容调整为原来的5倍和10倍，得到各个位置故障时保护动作量，如附录A 表A6所示。对比表A5、A6可以看出：对于区内故障，分布电容电流会使得保护动作量有所增大，有助于提高保护动作的可靠性；对于区外故障，分布电容电流会导致保护动作量增加，但是增大幅度较小，仍远小于整定阈值，不会引起保护误动。主要原因在于，发生区外故障时，MMC 子模块放电电流和非本段分布电容电流均为穿越性电流，且远大于本线电容电流，两侧电流波形仍能保持良好的相似度，不会导致保护误判。因此，本文所提纵联保护方案具有良好的耐受分布电容电流的能力。

5 结论

本文根据主动限流型直流配电网的特点，对其故障电流特性进行了分析，在此基础上，提出了一种基于改进DTW 算法的直流配电网线路纵联保护新原理，并进行了仿真验证。主要结论如下。

1）主动限流型配电网在其线路上一般不配置限流电抗器等边界元件，主动限流后，故障电流水平较低，且受故障点位置影响较小，这些因素导致单侧量保护难以应用，需综合利用线路两侧信息进行故障判断。

2）本文提出的基于改进DTW 算法的纵联保护新方案，具有良好的耐同步误差的能力，无须附加其他采样同步措施，易于工程应用。仿真结果表明，所提保护方案在不同电网运行方式下均可正确区分区内、外故障，同时具有良好的耐受过渡电阻和分布电容电流的能力。

附录见本刊网络版（http：//www.epae.cn）。