基于扰动电压定向的自适应电流源侵入式序阻抗测量

杨文莉，马俊鹏，孙瑞婷，王顺亮，赵静波，刘天琪

（1. 四川大学 电气工程学院，四川 成都 610065；2. 国网江苏省电力有限公司电力科学研究院，江苏 南京 211103）

0 引言

在碳达峰、碳中和国家战略目标下，清洁能源的开发与利用进一步加速，传统电力系统正向着高比例新能源发电和高比例电力电子设备（“双高”）方向发展，宽频振荡现象随之产生［1⁃4］。阻抗分析法是分析宽频振荡现象的重要工具［5⁃6］。由于系统内部参数的不确定性和系统拓扑的时变特性，获取系统输入／输出阻抗的数学解析式十分困难。近年来变流器输出阻抗的实测评估得到国内外学者的关注。

阻抗测量方法分为非侵入式测量［7⁃11］和侵入式测量［12⁃17］。非侵入式测量指通过提取待测系统固有背景谐波计算系统阻抗值；侵入式测量则是通过扰动注入电路向待测系统叠加扰动，并对电压、电流响应进行快速傅里叶变换分析，计算系统谐波阻抗。根据扰动注入方式的不同，侵入式测量法又进一步划分为串联注入电压法和并联注入电流法。并联注入电流法结构简洁，即插即用性强，因此本文选取并联注入电流法进行电网和逆变器阻抗测量。

变流器阻抗幅值、相角在不同频率处均表现出不同特性［18⁃20］，采用串联注入电压法进行宽频阻抗测量时，若待测系统阻抗极小（串联谐振点），则扰动电流将过大，采用并联注入电流法进行宽频阻抗测量时，若待测系统阻抗极大（并联谐振点），则扰动电压将过大。不论是扰动电压还是扰动电流过大，一方面会破坏待测系统稳定性，另一方面会导致扰动注入电路因输出功率过大而调制饱和。为安全精确地测量待测系统宽频阻抗，须对扰动能量进行自适应调整。

传统扫频法大多采用等间隔扫频，即以固定步长改变注入扰动电压／电流频率，以获取不同频率处的阻抗值。为缩短测量时间，大量研究开始采用Chirp、多正弦信号［12］等宽频信号实现一次注入扫频，然而这2 类方法均未考虑待测系统谐振点对扫频的影响。文献［13］提出采用二叉树法自适应调整频率步长，阻抗变化率越小，步长越大，该方法虽缩短了测量时间，但待测系统固有谐振点对扫频的影响并未消除。文献［14］采用级联H桥作为扰动注入电路，深入探讨了H 桥直流电压不平衡机理及平衡控制方法，对扰动变量仅进行开环控制，当待测系统谐振点位于测量频段内时，待测系统稳定性极易被破坏，H 桥平衡控制策略将因输出功率过大而失效，因此该方法仅适用于简单阻抗网络测量。文献［15］通过蝶形扰动电路向待测系统注入Chirp 扰动信号来测量铁路牵引供电系统阻抗值，Chirp 信号包含丰富的谐波，且各谐波分量幅值一致，虽在一定程度上提高了测量精度，同时也增大了待测系统在测量过程中的潜在失稳风险。文献［16］对扰动信号进行闭环幅值控制，维持扰动信号幅值在全测量频段内恒定，然而当扰动信号频率接近甚至等于待测系统串联谐振频率时，待测系统将失稳，扫频将被迫中止。文献［17］提出在阻抗测量过程中，需规避系统谐振点，在待测系统谐振点附近的频段不进行扫频操作，然而在实际测量过程中，待测系统谐振频率未知，难以人为预先规避。

针对并网变流器宽频阻抗特性复杂、待测系统谐振点难以预测的特点，本文提出了一种基于扰动电压定向的自适应电流源侵入式序阻抗测量方法，根据待测系统特性自适应调整扰动电流强度，进而自适应调整阻抗测量装置输出功率，兼顾待测系统稳定性的同时，提高阻抗测量精度。最后，通过仿真和半实物实验验证了所提算法的正确性和有效性。

1 电流源侵入式序阻抗测量装置系统描述

1.1 扰动注入单元

阻抗测量装置由扰动注入单元、信号处理单元和阻抗拟合单元构成，其中扰动注入单元是阻抗测量装置的核心。图1（a）为电流源侵入式阻抗测量装置及待测系统整体结构示意图。图中：PMSG 为永磁同步电机；zg为电网阻抗；ug为电网电压；upcc为T1低压侧电压；ipcc1为逆变侧输出电流；ipcc2为流过zg的电流。待测系统为风机并网系统，并网逆变器经升压变压器T1接入电网。加入测量装置前，待测系统公共耦合点PCC（Point of Common Coupling）处的电压、电流稳态值分别为Ugpcc、Igpcc。为了降低阻抗测量装置电压等级，测量点放置于T1的690 V 低压侧。图1（b）为扰动注入单元的电路结构，扰动注入单元由不控整流电路、双向DC-DC电路和带LC滤波器的三相逆变器构成。图中：C1为不控整流电路输出端口的滤波电容；uin为C1上的电压；C2为双向DC-DC电路输出端口的滤波电容；udc为C2上的电压；Lf为逆变电路输出端口滤波电感；Cf为逆变器电路输出滤波电容；iL为流过Lf的三相电流；idis为扰动注入电路产生的三相扰动电流。

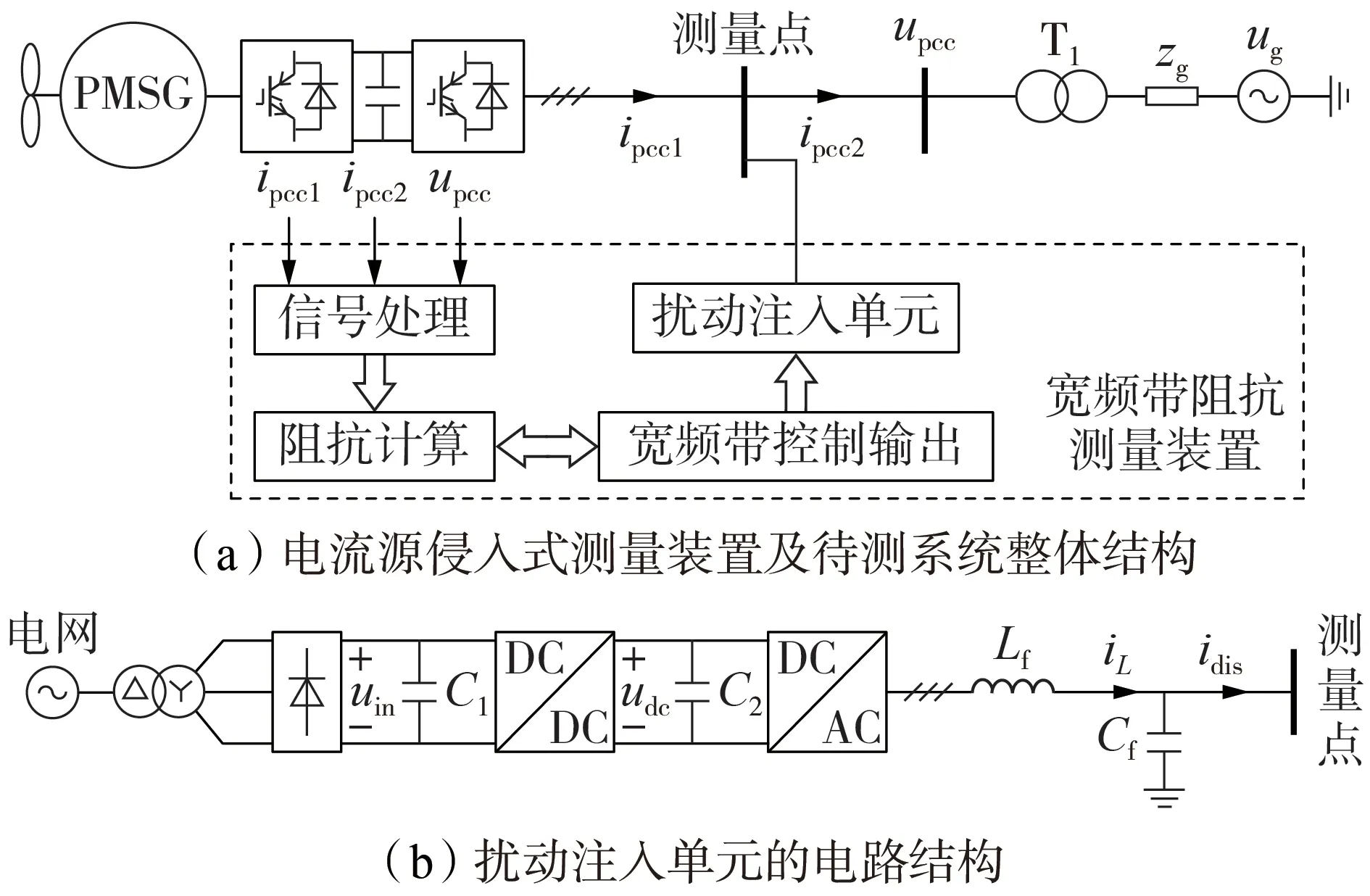
图1 电流源侵入式序阻抗测量装置整体结构示意图Fig.1 Schematic diagram of overall structure of current source intrusive sequence impedance measurement device

注入扰动电流时，必须保证并网逆变器稳态工作点不变，故需要保证待测系统中的基波分量不流入扰动注入电路。因此，扰动注入电路的控制目标分为2 个部分：①输出设定幅值、频率、初始相角的扰动电流；②保证阻抗测量装置的加入不改变待测系统的稳态运行点。

1.2 控制策略

通过不控整流电路给双向DC-DC 电路供电，其输入电压为uin，双向DC-DC 电路采用定电压控制，为逆变电路直流侧提供恒定的直流电压udc。双向DC-DC电路及其控制框图见附录A图A1。

图2（a）为扰动注入单元电路中逆变器总体控制框图，基波控制器用于保持待测系统稳态工作点不变，扰动控制器用于控制所注入的谐波电流。图中：vg为基波控制器产生的参考电压；vh为扰动控制器产生的参考电压；v为逆变器控制器输出的双频参考电压。图2（b）为基波控制器控制框图，采用基于电网电压定向的恒流控制策略。图中：GN1（s）表示中心频率为扰动信号频率fh的陷波器传递函数；ig为iL中的基频分量；为upcc中的基频分量；igd、igq分别为ig的d、q轴分量；θg为的相角；vgd、vgq分别为vg的d、q轴分量；PLL 为锁相环；PI为比例积分控制器。为了实现待测系统与测量装置之间无基波电流交互，基波电流参考值的d、q轴分量分别为：

图2（c）为扰动控制器控制框图，采用恒流控制策略。图中：GN2（s）表示中心频率为基波频率fg的陷波器传递函数；ih为iL中的扰动电流分量；ihd、ihq分别为ih的d、q轴分量；θh为ih的相角，θh=2πfh；vhd、vhq分别为vh的d、q轴分量。扰动电流幅值进行闭环控制，其参考值的d、q轴分量分别为：

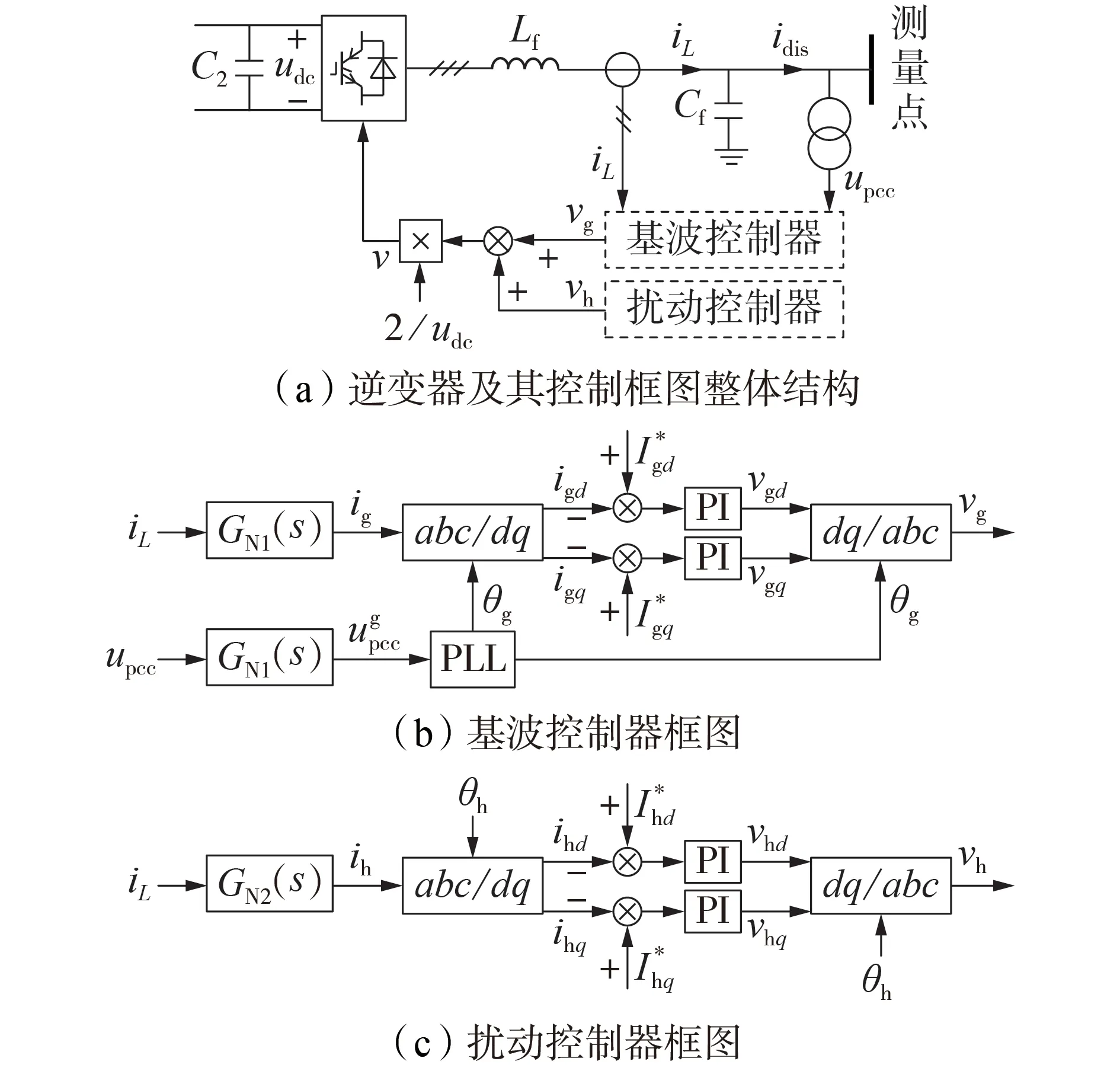
图2 逆变器控制框图Fig.2 Control block diagram of inverter

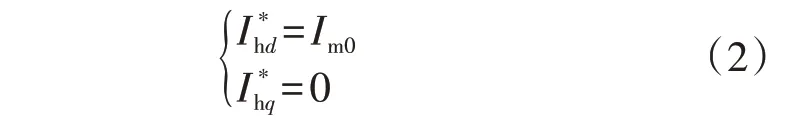
式中：Im0为扰动电流幅值参考。

稳态时，vh与待测系统谐波阻抗相关，vg=Ugpcc。由于udc大小恒定，当待测系统阻抗值超过临界阻抗值zc时，仍然输出幅值为Im0的扰动电流会导致调制饱和，即v的幅值超过0.5udc，此时基波控制器和扰动控制器均会失稳，影响阻抗测量的同时也会严重干扰待测系统的稳定性。为了测量宽频段阻抗，在扰动控制器中引入抗饱和策略，自适应调整输出扰动电流的强度。

积分器是诱发调制饱和的主要原因。当进行宽频阻抗测量时，传统带积分抗饱和的PI 控制器控制参数难以整定，因此实际应用中往往通过反复实验确定限幅值及抗饱和系数［21］。然而，当参数选取不合理时，无法规避过调制，甚至会导致系统失稳，抗饱和策略的参数整定问题亟待解决。

2 基于扰动电压定向的扰动电流自适应控制策略

2.1 控制框图

由于待测系统阻抗相角的不确定性，d、q轴积分器的输出电压难以预测，因而无法选取合适的限幅值。为解决该问题，提出基于扰动电压定向的扰动电流自适应控制策略，使得d轴PI 控制器输出的电压为扰动电压vh的幅值，q轴PI控制器的输出电压为0。图3 给出了基于扰动电压定向的扰动电流自适应控制策略框图。图中：Δim为扰动电流幅值参考的修正量；Kaw为抗饱和系数；i'm为修正后的扰动电流幅值参考；u'm为扰动电压幅值经限幅环节后的输出值。

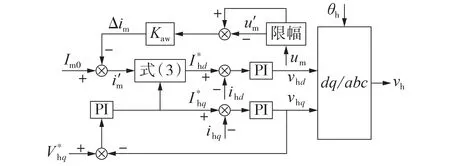
图3 基于扰动电压定向的扰动电流自适应控制策略Fig.3 Disturbance current adaptive control strategy based on disturbance voltage orientation

具体实现方式为将vhq与其参考值（=0）作比较得到扰动电流参考值的q轴分量。

同时，通过式（3）得到扰动电流参考值d轴分量，保证输出恒定幅值的扰动电流。

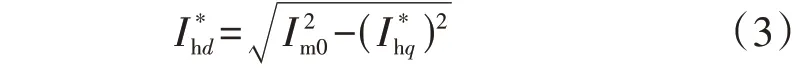
在采用基于扰动电压定向的扰动电流自适应控制策略后，只需对d轴积分器进行抗饱和处理即可避免过调制，降低了抗饱和积分器设计难度。抗饱和积分器本质上是改变PI 控制器输入信号的参考值，因此，本文在基于扰动电压定向的恒流控制策略基础上，提出一种新型抗饱和策略，如图3 所示。通过检测逆变器输出扰动电压幅值vhd，对扰动电流初始设定幅值Im0进行自适应调整。当逆变器输出电压幅值um小于等于限幅值Ums时，抗饱和策略不起作用，Im0不变；当um大于Ums时，在Im0中叠加Δim，见式（4）和式（5）。

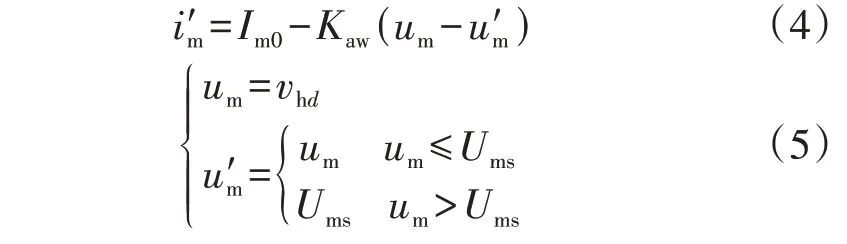
式中：Kaw为抗饱和系数。

通过调整扰动电流幅值大小，既可以避免阻抗测量装置饱和，也可避免扰动电压过大诱发的待测系统失稳问题。

2.2 参数整定

加入抗饱和策略后，需要对Ums及Kaw进行合理选取。首先对Ums进行整定。采用扰动电压定向的扰动电流自适应控制策略后，限幅值Ums为：

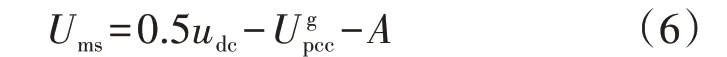
式中：A为裕量系数。然后对Kaw进行整定。稳态时，逆变器输出电压幅值um、修正后的扰动电流幅值参考i'm与待测阻抗幅值zx之间满足：

将式（7）代入式（4）：

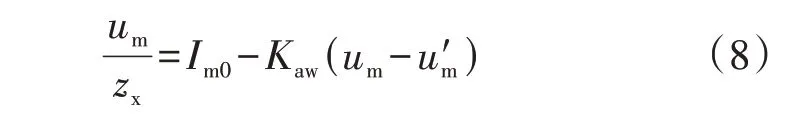
整理得：

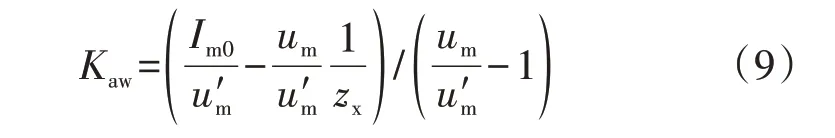
由式（9）可知，Kaw的取值范围由um、u'm及zx共同决定。其中当抗饱和策略起作用时，u'm为常数Ums；zx为待测系统的固有特性，与待测系统的频率有关，为不可控量。在某一特定频率点fhx处，zx视为常数，此时，Kaw的取值范围仅取决于um。下文将对um的取值范围进行分析。

对um进行一定约束，可保证阻抗测量装置不出现过调制现象。当抗饱和策略运行时，um满足：

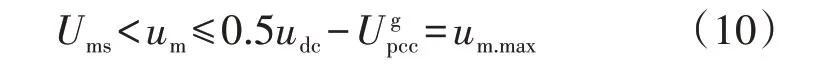
式中：um.max为um的上限值。通过式（6）、（9）、（10）可得Kaw在某一特定工作点下的取值范围为：

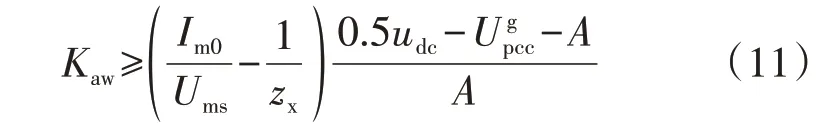
为保证阻抗测量装置在全频段内均工作在线性工作区，需保证对于任意的zx（zx∈[zc，zmax]），式（11）始终成立。其中zc代表um=Ums时待测系统阻抗值，即：

zmax为阻抗测量装置可测的最大阻抗值，结合电流传感器精度Ai可得：

为保证等式（11）始终成立，需要求解式（11）不等号右端表达式的最大值，保证Kaw始终大于该最大值。令N为式（11）不等号右端的表达式，即：

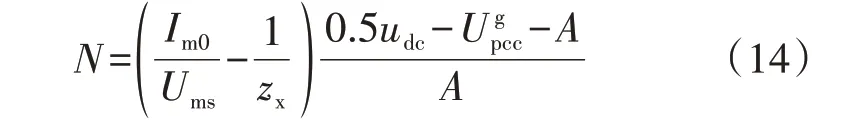
绘制N随zx变化的曲线图，如图4所示。当待测系统阻抗为最大值zmax时，N取得最大值K。因此，保证Kaw≥K，即可实现阻抗测量装置全频段内不出现过调制现象。

图4 N随zx变化的曲线Fig.4 Curve of N vs. zx

3 仿真验证

阻抗测量装置参数选取参考文献［22］，具体参数见附录A 表A1。待测系统为恒流控制的三相并网逆变器，待测系统结构及其控制框图见附录A 图A2。待测系统PCC 处电压稳态值Ugpcc=1 485 V，电流稳态值Igpcc=1000 A。扰动电流幅值参考Im0取待测系统PCC 处电流稳态值Igpcc的10%（100 A）。设裕量系数A=5，电流传感器精度Ai=5%，将以上参数代入式（6）、（11）—（14），Kaw整定为10。序阻抗物理意义明确，测量过程简便，基于序阻抗的稳定性判据适应范围广［23］，因此本文对并网逆变器正序阻抗及电网正序阻抗进行测量。

图5 为采用传统控制策略进行单频扫描时的波形，图中im为实际输出的扰动电流幅值。设［0，0.5）s阻抗测量装置不工作，无输出；［0.5，1）s注入频率为10 Hz的扰动电流；［1，1.5）s注入频率为510 Hz的扰动电流；［1.5，2）s 注入频率为996 Hz 的扰动电流；［2，2.5）s注入频率为1496 Hz的扰动电流；［2.5，3］s注入频率为1 990 Hz 的扰动电流。由图可知，当采用传统控制策略单频扫描方式向待测系统注入恒幅值扰动电流时，待测系统在1.5 s 开始失稳，此时实际输出值无法跟踪参考值，控制器输出的调制信号幅值超过上限值um.max。即当注入频率为996 Hz 的扰动电流时，待测系统阻抗过大，引起测量装置调制饱和，进而失稳，同时由于积分器对误差的积累作用，该失稳现象愈演愈烈。

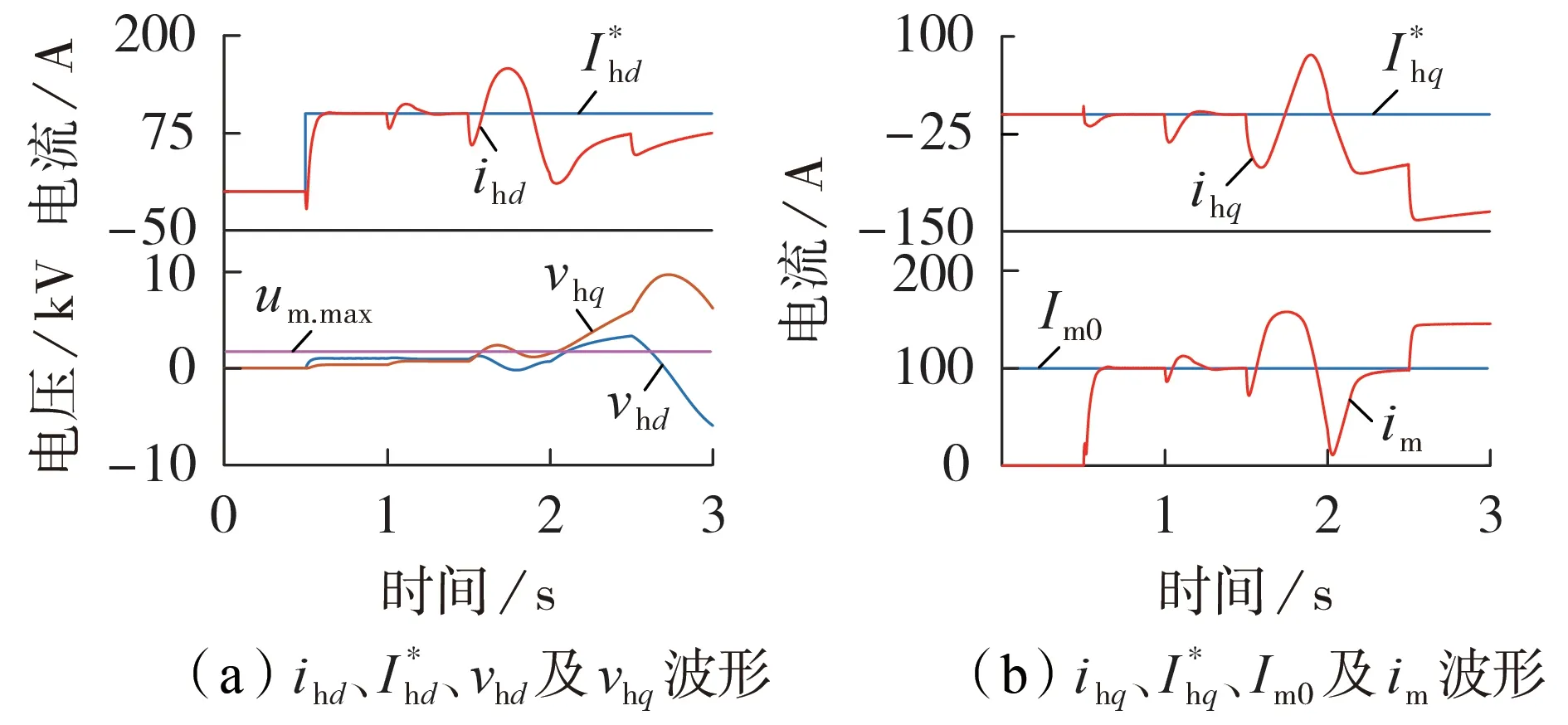
图5 传统控制策略下单频扫描波形Fig.5 Single-frequency sweep waveforms under traditional control strategy

图6 为采用自适应控制策略进行单频扫描时的波形。设［0，0.5）s 阻抗测量装置不工作；［0.5，1）s注入频率为10 Hz、幅值为100 A 的正弦扰动电流，此时阻抗测量装置工作在恒流模式；［1，1.5）s 注入频率为510 Hz、幅值为100 A 的正弦扰动电流，此时阻抗测量装置仍然运行在恒流模式；［1.5，2）s 扰动电流频率变化为996 Hz，此时抗饱和策略投入运行，扰动电流幅值自适应调整为97 A；［2，2.5）s 扰动频率变化为1 496 Hz，抗饱和策略继续作用，扰动电流幅值自适应调整为51 A；［2.5，3）s 扰动电流频率为1990 Hz，扰动电流幅值自适应调整为95 A。由图可知，采用自适应控制策略进行单频扫描时，无需规避待测系统谐振频率点，扰动电流频率可以任意选择，扰动电流幅值自适应调整。仿真结果验证了自适应控制策略的有效性。

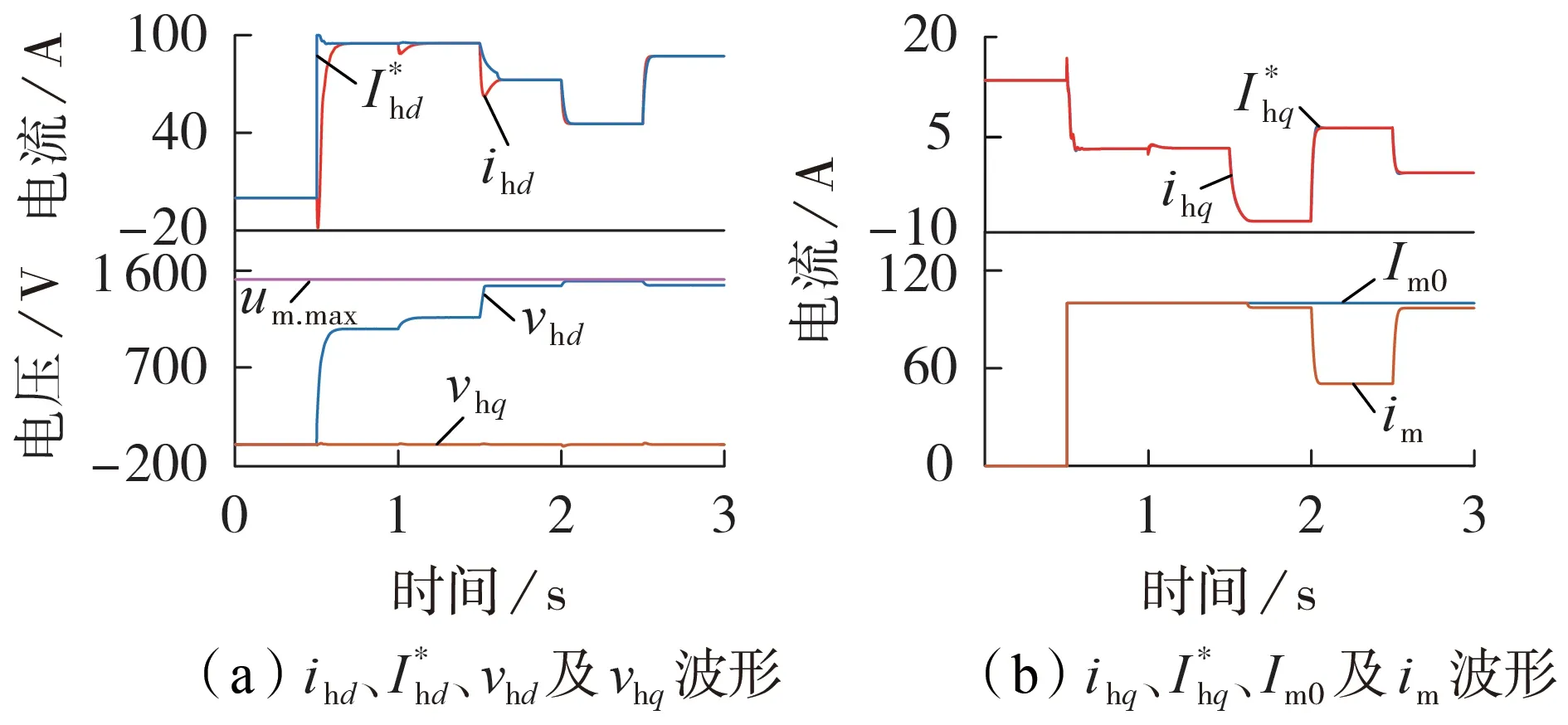
图6 自适应控制策略下单频扫频波形Fig.6 Single-frequency sweep waveforms under adaptive control strategy

进行宽频扫描时，注入的扰动电流为Chirp 信号，fh随时间线性变化：

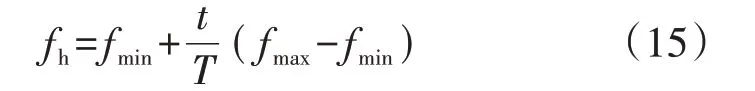
式中：T为Chirp信号的周期；fmin、fmax分别为时间周期内的最小、最大频率。宽频扫描波形见附录A图A3。

采用自适应控制策略进行单频扫描和宽频扫描时，扰动电流幅值均可以快速灵活地进行自适应调整，验证了所提控制策略的有效性。由上述分析可得，传统控制策略与自适应控制策略的差异性体现在fh>900 Hz 时。当fh≤900 Hz 时，对应频段内的待测系统阻抗值较小，不会诱发待测系统调制饱和，因此传统控制策略与本文所提自适应控制策略的扫频效果一致。然而，当fh>900 Hz 时，待测系统阻抗幅值过大，保持输出扰动电流幅值恒定会诱发测量装置调制饱和，进而影响测量精度。图7 展示了fh>900 Hz 时，传统控制策略及自适应控制策略的阻抗拟合结果。由图可知，所提控制策略在待测系统高阻频段内仍保持着高测量精度，验证了本文所提控制策略的有效性。

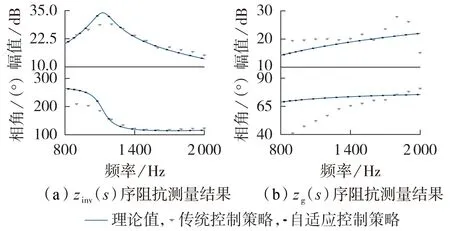
图7 不同控制策略下阻抗拟合结果Fig.7 Impedance fitting results with differentcontrol strategies

自适应控制策略单频及宽频扫描结果见附录A图A4、A5。从上述阻抗测量结果来看，所提阻抗测量策略既适用于更精确的单频扫描，也适用于测量时间更短的宽频扫描，扩大了阻抗测量的频率范围。

4 实验验证

为进一步验证本文所提控制策略，搭建基于RT-BOX 实时仿真器的硬件在环实验平台，实物图见附录A 图A6。利用上述实验平台对附录A 图A2所示待测系统进行单频扫描实验，Im0仍设为100 A。采用基于扰动电压定向的扰动电流自适应控制策略注入频率分别为10、552 Hz 的扰动电流，实验波形见附录A图A7。

图8（a）为注入频率为1 510 Hz 扰动电流时采用基于扰动电压定向的扰动电流自适应控制策略的实验波形，扰动电流幅值自适应调整为52 A。图8（b）为注入频率为1 510 Hz 扰动电流时采用无抗饱和策略的实验波形，此时测量装置运行失稳，并且由于扰动电压过大，待测系统亦产生振荡现象。由图8可知，当待测系统阻抗过大时，若不对扰动电流进行自适应调整，则不仅影响阻抗测量装置的正常运行，还严重干扰了待测系统的稳定运行，采用本文所提扰动电流自适应控制策略可有效提高系统的稳定性。

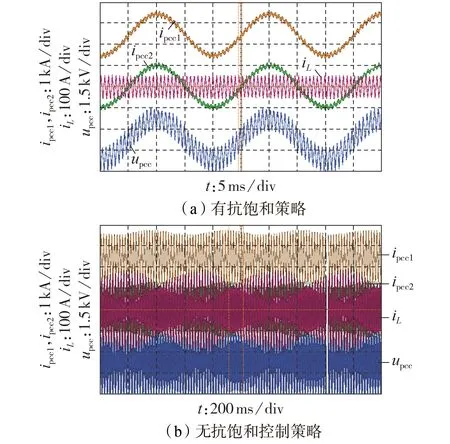
图8 注入1510 Hz扰动电流时有、无抗饱和策略的实验波形Fig.8 Experiment waveforms of 1510 Hz current disturbance injection with and without anti-saturation strategies

图9（a）、（b）分别为逆变器正序阻抗zinv（s）和电网正序阻抗zg（s）实测结果。由图可知，实验测量结果与理论曲线高度重合，进一步验证了本文所提控制策略的有效性。

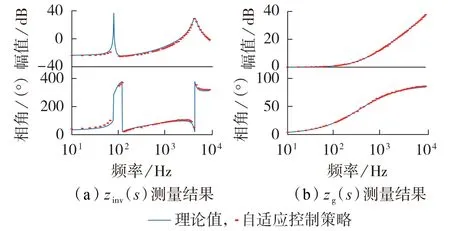
图9 阻抗实测结果Fig.9 Results of impedance measurement

5 结论

本文围绕大功率阻抗实测装置，针对并网变流器宽频阻抗特性复杂，待测系统谐振点难以预测的特点，提出了一种基于扰动电压定向的自适应电流源侵入式序阻抗测量方法，结合抗饱和策略，实现了扰动电流自适应调整。同时，对抗饱和策略的参数进行优化整定。通过仿真和半实物实验验证了所提方法的有效性，可得如下结论：

1）基于扰动电压定向的扰动电流自适应控制策略限幅值选取方便，可以有效规避由于待测系统高阻抗诱发的过调制现象；

2）扰动电流自适应控制策略可以根据待测阻抗值灵活调节扰动电流强度，阻抗测量过程中无须规避谐振点，保证了阻抗测量装置在全频段的稳定运行，仿真及半实物实验验证了该策略的有效性；

3）扰动电流自适应控制策略既适用于高精度单频扫描，也适用于快速宽频扫描，实际测量过程中可根据需求灵活选取。

附录见本刊网络版（http：//www.epae.cn）。