模拟直流电机调速特性的双向DC／DC变换器虚拟直流电机控制策略

支 娜，明 旭，张林杰，张 辉，张伟亮

（西安理工大学 电气工程学院，陕西 西安 710048）

0 引言

为实现我国能源转型，完成碳达峰、碳中和的远景目标，低压直流微电网作为新一代低碳高效的能源体系，受到广泛关注［1⁃2］。直流微电网中，分布式能源、储能设备以及各种交直流负载均通过电力电子装置接入直流母线［3］，而电力电子装置均为非旋转静止元件，不具备传统电机的转动惯性和阻尼特性，因此直流微电网呈现低惯性特性［4⁃5］。增加虚拟惯性调节，提升直流微电网的惯性特性，实现网内有功功率自主均衡［6⁃7］，是直流微电网可靠稳定运行的基础［8⁃9］。

目前，虚拟惯性的研究主要应用于交流电网中逆变器控制，对直流微电网的相关研究较少，主要包括附加惯性控制［10⁃11］、虚拟电容控制［12⁃14］和虚拟直流电机VDCM（Virtual DC Machine）控制［15⁃17］。文献［10］提出了一种附加惯性控制策略，在原有的下垂控制中附加了惯性控制环节，模拟电容的工作原理来调度额外功率，并且引入高通滤波器代替微分环节，从而引入惯性特性；文献［11］将文献［10］中的高通滤波器替换成一阶惯性环节，避免高通滤波器带来的高频干扰。文献［12］将交流电网中应用较为成熟的虚拟同步电机VSG（Virtual Synchronous Generator）技术类比引入直流微电网中，通过控制双向并网变换器引入虚拟惯性，改善了直流母线电压动态性能；文献［13］提出了一种用于直流微电网的自主虚拟电容控制策略，在传统双环控制之前加入下垂控制和虚拟电容控制，通过改变虚拟电容和虚拟阻抗降低电压变化率，解决直流微电网惯性低、稳定性差的问题；文献［14］提出了一种协调电流共享算法的级联虚拟惯性控制，在双向DC／DC 变换器和双向并网逆变器中引入统一的虚拟惯性控制。文献［15］将直流电机数学模型和蓄电池侧双向DC／DC变换器进行等效类比，提出了一种VDCM 控制策略，将直流电机的惯性特性和阻尼特性引入变换器中，提高了直流母线电压稳定性能；文献［16］在传统电压电流双闭环控制中加入VDCM 环节，为系统提供惯性支持；文献［17］将交流侧和直流侧融合统一的虚拟电机控制，在并网运行时能够降低直流微电网内部功率波动对主电网的冲击。上述文献中，附加惯性控制需要在原有控制基础上增加惯性模型，控制结构较为复杂，不利于电力系统长时间运行；虚拟电容控制需要考虑电流输入和反馈带来的谐波以及超调问题，参数设计较为困难；VDCM 控制将直流电机和双向DC／DC 变换器进行等效类比，在控制策略中模拟直流电机运行特性，能够同时为直流微电网提供惯性和阻尼，因此本文选取VDCM 为研究对象。

传统VDCM 控制均为稳态模型，忽略了电枢电感对电枢电流的动态调节过程，而电力电子变换器在负载扰动、分布式电源功率波动时，直流母线电压的动态调节过程会直接影响直流微电网的稳定运行。本文在P-U下垂控制基础上，引入直流电机动态调速特性，得到一种新型VDCM 控制策略。首先将直流电机和双向DC／DC 变换器进行等效类比，从数学模型和控制策略两方面进行论述，并对P-U下垂控制所缺特性进行剖析。其次依照直流电机定转子绕组间的电磁感应作用，模拟直流电机外环调速环节在P-U下垂特性曲线中引入动态数学模型；模拟直流电机电流内环机械惯性特性将P-U下垂控制中的电流环改进为惯性阻尼环节，由此得到新型VDCM 控制策略。建立加入新型VDCM 控制策略后的双向DC／DC 变换器小信号模型，讨论参数变化对系统稳定性的影响规律。最后构建光储孤岛直流微电网仿真和实验平台，针对所提策略对于直流母线电压稳定性的提升作用进行验证。

1 直流电机与直流微电网的传统控制

1.1 直流电机的数学模型及其调速过程

直流电机的动态数学模型描述了各参数在电流过渡过程中的变化规律，是分析和计算电力拖动系统动态行为的基础。不同方向的电枢电流ia分别代表直流电机工作在发电机模式或电动机模式，其指向电枢端时直流电机在电动机模式，其指向外端时直流电机工作在发电机模式。以直流电动机为例，其等效电路如图1 所示。图中：Ra、La分别为电枢绕组的电阻、电感；Ua、ea和ia分别为机端电压、电枢电压和电流；vf、if分别为励磁电压与励磁电流；rf、Lf分别为励磁电阻与励磁电感；ω为电机转动角速度；J为转动惯量。

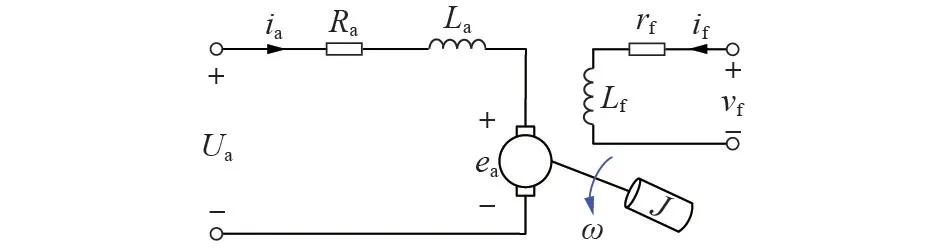
图1 直流电动机等效电路图Fig.1 Equivalent circuit diagram of DC motor

直流电动机的动态数学模型为：

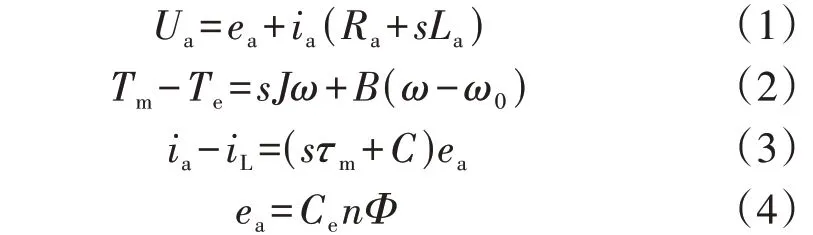
式中：Te和Tm分别为机械转矩和负载转矩；B为阻尼系数；ω0为额定角速度；iL为负载电流；Ce为电势常数；n为转速；Φ为每极主磁通；τm和C分别为机械时间常数和阻尼常数。

根据式（1）—（4）搭建直流电动机动态调速框图，见附录A 图A1。可看出直流电机动态调速过程为：负载电流iL增大，转速n下降，ea下降，Ua不变，Ua和ea差值增大，ia增大，n回升。

1.2 双向DC／DC变换器的P-U下垂控制

直流微电网中储能侧双向DC／DC 变换器拓扑结构如图2 所示。图中：ub、ib分别为蓄电池电压及其输出电流；Lb和rb分别为蓄电池侧电感和电阻；S1和S2为开关管；iout和idc分别为双向DC／DC 变换器的前端和后端输出电流；Cb为直流侧电容；icap为电容电流；udc为直流母线电压；e为S1在开关周期内的平均电压。

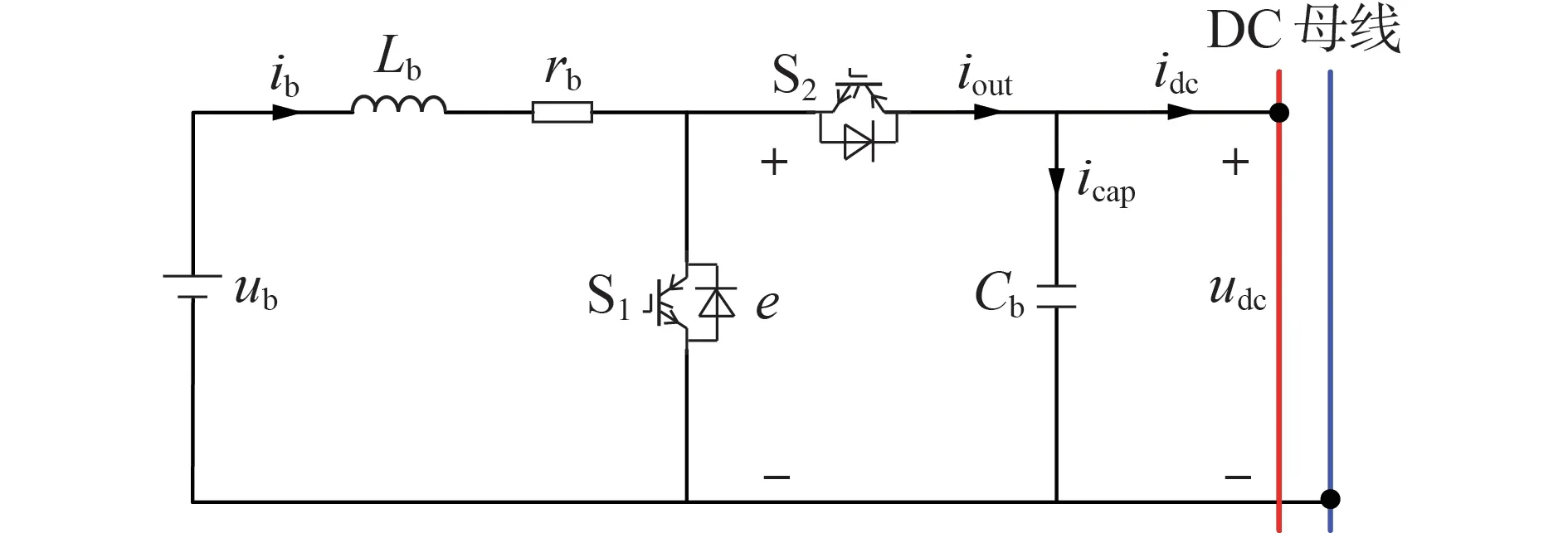
图2 双向DC／DC变换器拓扑图Fig.2 Topology diagram of bidirectional DC／DC converter

不同方向的ib分别代表双向DC／DC 变换器工作在Buck和Boost的2种模式，其指向直流母线时双向DC／DC 变换器工作在Boost 模式，其指向储能侧时双向DC／DC 变换器工作在Buck 模式。以Boost模式为例，P-U下垂曲线表达式为：

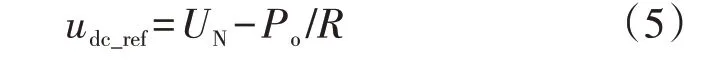
式中：udc_ref和UN分别为直流母线电压参考值和额定值；Po=udcidc为变换器输出功率；R为虚拟电阻，式中以1/R表示下垂曲线系数。

双向DC／DC 变换器P-U下垂控制框图如附录A 图A2 所示。具体调压过程为：直流侧负载功率增加时，蓄电池输出电流ib增加，直流母线电压udc降低，udc_ref不变，udc_ref与udc偏差增加，重新增加蓄电池输出电流参考值ib_ref，udc回升。

2 新型VDCM控制模型

2.1 直流电机与双向DC／DC变换器的等效类比

图2中双向DC／DC变换器的动态数学模型为：

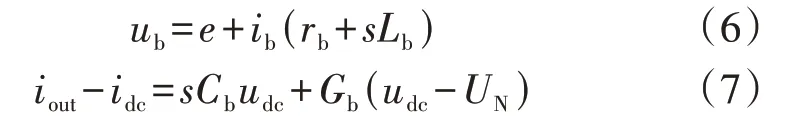
式中：Gb为直流侧电容导纳。

分别对比式（1）和式（6）、式（2）和式（7），可看出直流电机和双向DC／DC 变换器的数学模型在组成形式上高度类似，两者等效电路图中的参数可分别进行类比等效，等效对照参数见附录A 表A1。再对比附录A 图A1、A2，可看出直流电机调速过程和储能变换器调压过程也具有高度类似性，因此两者在控制框图上也可进行等效类比。由此将直流电机与双向DC／DC变换器等效联系。

对于直流电机动态调速过程，iL变化会导致n偏离额定值，ea随之变化，微分项sLa在ea变化瞬间快速作用于误差变化率，因此直流电机外环下垂控制可起到快速动态调节作用。内环控制为直流电机惯性阻尼调节，τm决定直流电机响应速度，并提供足够惯量防止n突变，C提供足够阻尼，对n的变化起阻碍作用，因此电流内环所提供的惯量在转速改变瞬间维持原运动状态不变，同时阻尼特性能够提升直流电机的抗扰性能。

而双向DC／DC 变换器P-U下垂控制实质上由功率环（P-U下垂曲线）、电压环（比例积分PI（Proportional Integral）控制）和电流环（PI 控制）组成，并不具备直流电机动态调速过程中的外环动态调节和内环惯性阻尼调节，导致直流微电网应对负载功率突变时的调节能力较差。为使双向DC／DC变换器具有与直流电机类似的调节特性，将直流电机的动态下垂调节以及电流内环惯性阻尼调节思想引入双向DC／DC 变换器控制中，能够提升直流微电网中电力电子变换器的动态特性以及惯性阻尼特性，提高直流微电网的运行稳定性。

2.2 VDCM控制策略

首先，模拟式（1）及直流电机外环转速动态下垂调节过程，在P-U下垂控制中引入微分环节，使其能够在负载动态变化瞬间减小误差变化率，调整直流母线电压突变瞬间超调量，在不影响稳定性的前提下提前修正输出信号，增加阻尼，提升响应速度［18⁃19］。由于负载稳态运行时微分作用失效，改进后的P-U下垂控制方程为：

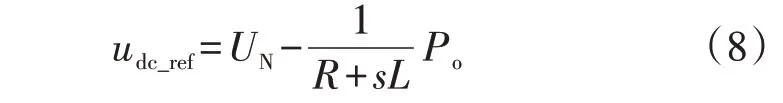
式中：L为虚拟电感，表示微分系数。

对式（8）中的微分环节sL进行分析，绘制其阶跃惯性响应性曲线，如图3（a）所示。由图可知：令未加入微分作用前（L=0）的直流母线电压变化量Δudc输出为阶跃惯性响应曲线，L=0.01 mH 时，对阶跃惯性上升过程中的变化量逐步进行微分计算，此时Δudc超调尖峰值为1 V；L=0.05 mH 时，Δudc超调尖峰值为0.5 V；L=0.1 mH 时，Δudc超调尖峰值为0.1 V，可见微分系数L越大，阶跃惯性响应经过微分环节后输出的Δudc超调尖峰值越小。因此，在双向DC／DC变换器P-U下垂控制中引入动态微分环节，在保证稳定性的同时也能够降低直流母线电压变化时的超调量，增强直流微电网动态调节效果。

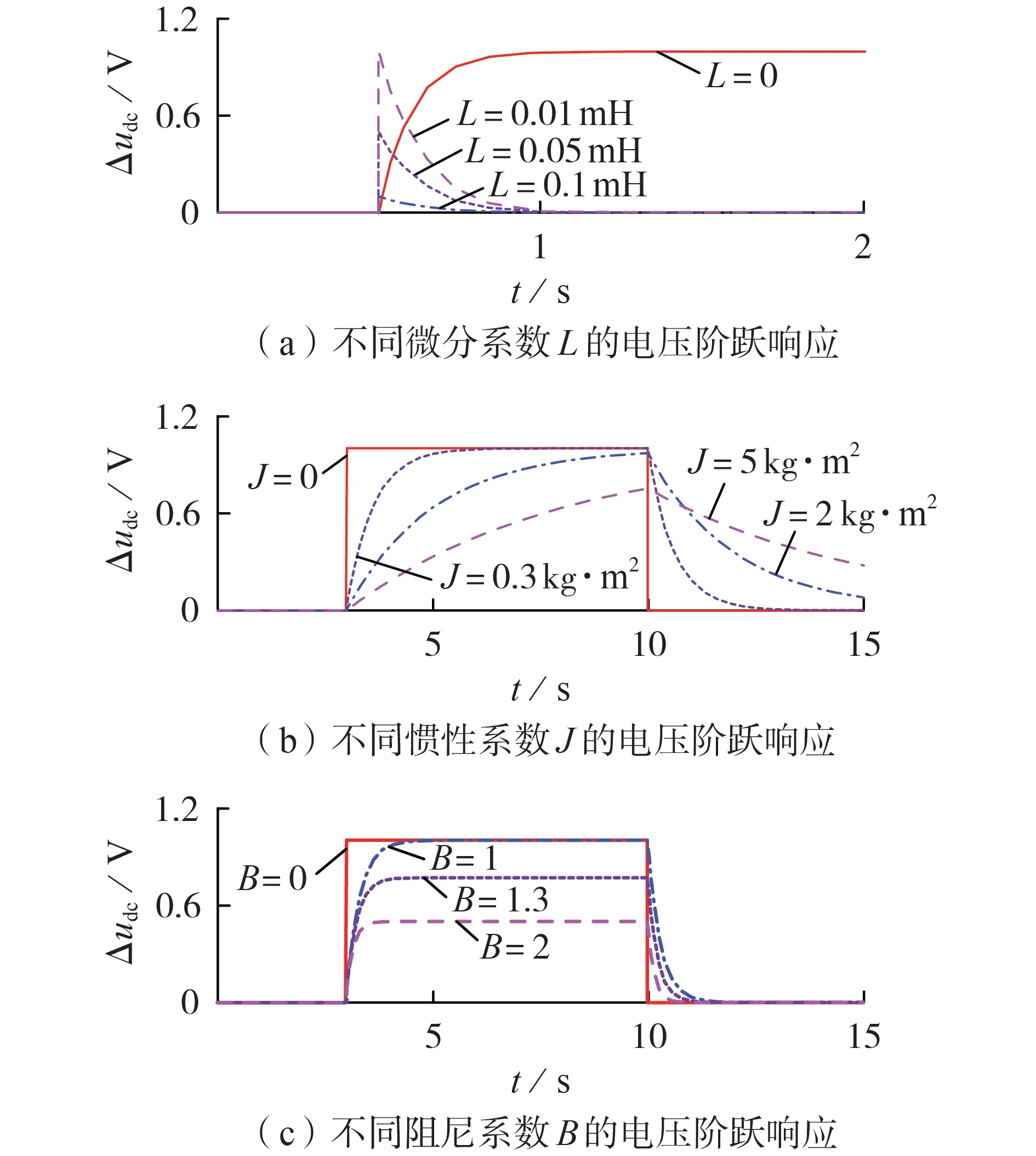
图3 控制参数变化时Δudc响应波形图Fig.3 Response waveform diagram of Δudc when control parameters change

其次，直流微电网中直流侧电容Cb能够对直流母线电压变化起到缓冲抑制作用，但相比直流电机中的转动惯量J和阻尼系数B而言，其值较小并不足以为直流微电网提供足够惯性支撑［20］。在双向DC／DC 变换器的P-U下垂控制中，电流内环表达式为：

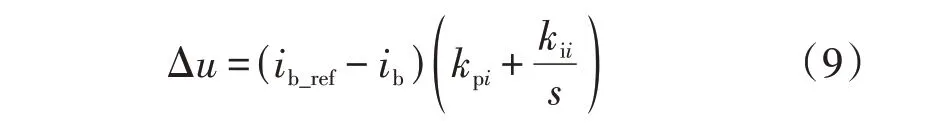
式中：kpi、kii分别为电流环比例、积分系数；Δu为脉冲宽度调制PWM（Pulse Width Modulation）波的输入信号。

直流电机中电流内环表达式可由式（3）变形为：

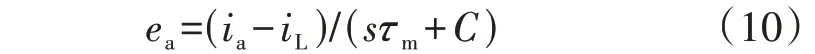
式（9）和式（10）同样作为电流内环表达式，对比可知式（9）不具备式（10）中的惯性阻尼调节。为了模拟直流电机电流内环惯性阻尼调节过程，在P-U下垂控制的电流内环中引入惯性环节，改进后表达式为：

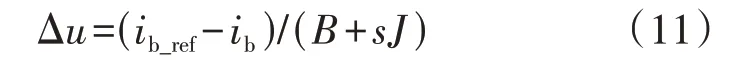
与传统的惯性环节引入方式不同，本文直接将电流的PI 控制器改进为惯性环节调节器，理论上功率环可控制输出功率的大小，在电压稳定时（电压环PI 控制），可保证输出电流的稳定，惯性环节的引入为双向DC／DC 变换器提供额外惯性与阻尼，增强直流微电网运行稳定性。由式（11）得到新型VDCM控制策略中电流内环控制器传递函数Gi(s)为：

由式（12）绘制参数J、B的响应特性。图3（b）中：令转动惯量J=0，此时Δudc输出为阶跃脉冲曲线；J=0.3 kg·m2时，Δudc在阶跃脉冲上升沿到来时刻缓慢上升，逐渐达到稳态值；J=2 kg·m2时，Δudc在阶跃脉冲上升沿到来时上升更加缓慢；J=5 kg·m2时可明显看出曲线还未上升到最高点，就随着阶跃信号下降沿时刻的到来被迫缓慢下降，由此可见，转动惯量J越大，阶跃信号上升越缓慢，选取合适转动惯量值，能够同时保证输出曲线上升／下降的速度以及输出曲线的平滑度。

图3（c）中：B=0 时，无阻尼作用；B=1 时，阻尼作用微弱；B=1.3 时，Δudc最高稳态值为0.78 V；B=2 时，Δudc最高稳态值为0.5 V，阻尼作用更强。由此可见，随着阻尼系数B的增加，阶跃响应的上升／下降速度无明显变化，上升后到达稳态的幅值更低，因此判断B仅对稳态值存在影响，选取合适的阻尼系数值能更好地抑制输出曲线的稳态波动。

综上，由理论分析可知：本文所提新型VDCM 控制策略模拟直流电机调速过程中的动态下垂调节特性，能够减小直流母线电压突变时的超调量且保证快速性；模拟直流电机电流内环惯性阻尼调节过程，为直流微电网提供额外惯性与阻尼，增强直流微电网运行的稳定性。最终得到的模拟直流电机调速过程的双向DC／DC变换器控制框图如图4所示。

图4 新型VDCM控制框图Fig.4 Block diagram of novel VDCM control

3 小信号稳定性分析

为分析改进VDCM 控制策略对变换器性能的影响，建立附录A 图A3 所示双向DC／DC 变换器小信号等效电路。据图A3 及理论推导得出各环节传递函数表达式，Δd到Δib传递函数Gid(s)、Δd到Δudc传递函数Gud(s)、电压环传递函数GPIu(s)、调制器传递函数Gm(s)的表达式分别为：

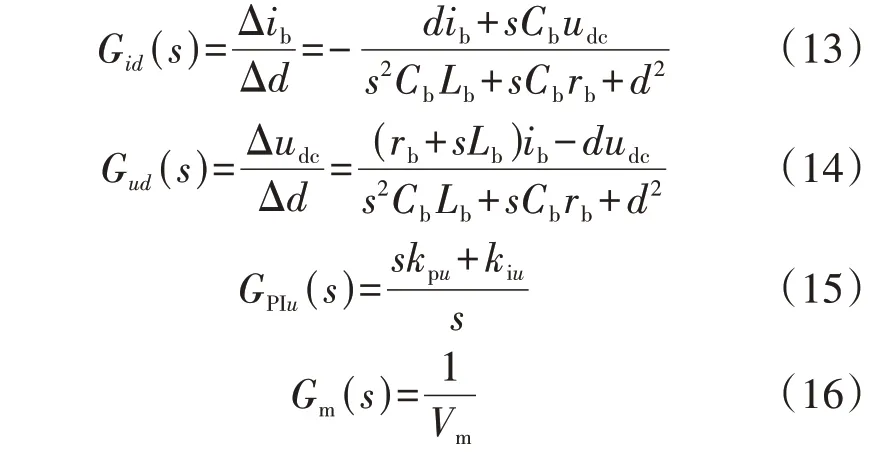
式中：kpu、kiu分别为电压外环比例、积分系数；Vm为载波峰值；Δudc为直流母线电压小扰动；Δib为蓄电池电流小扰动；Δd为占空比d小扰动。

结合VDCM 控制框图和双向DC／DC 变换器小信号等效电路，得到附录A 图A4 所示VDCM 小信号模型，其直流电压与变换器输出功率之间的开环传递函数Gup(s)为：

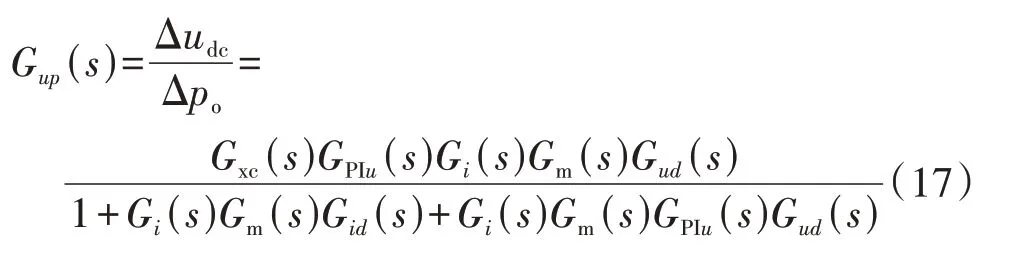
阻感特性下垂控制传递函数Gxc(s)为：

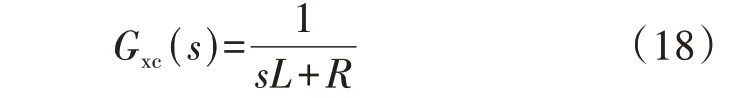
将各传递函数表达式代入式（17）并移项可得：

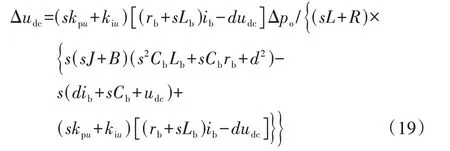
移项后的L、J、B都在分母中，以微分系数L变化为例：直流微电网中功率调节Δpo一定时，增大L会减小直流母线电压变化量Δudc，即L增大可抑制直流母线电压波动，J和B分析同理。由Gup（s）绘制开环传递函数Nyquist 曲线图和Bode 图，进一步探讨L、J、B这3 个参数变化对系统稳定性的影响。采用附录A 表A2 所示参数值，仿真结果如附录A 图A5 所示，定量分析如附录A表A3所示。

由图A5 可知：J增加，Nyquist 曲线逐渐远离点（-1，0），这说明系统稳定裕度随着J的增大而增大；由Bode图可知，J从0.001 kg·m2增加到0.1 kg·m2，幅值裕度由77.1 dB 增加到83.6 dB，穿越频率由1 150 rad／s 减小至479 rad／s。可见随着幅值裕度的增加，系统稳定性改善，但增加程度有限，因此增大J对稳定性提升有限；同时穿越频率减小，快速性变差。综上选取J=0.01 kg·m2。

B=10时，Nyquist曲线远离点（-1，0）距离跨度较为明显。Bode图中阻尼系数B从1增加到50，幅值裕度由75.2 dB 增加到101 dB，穿越频率由640 rad／s增加到1 720 rad／s。可见幅值裕度增加，一定程度上增加阻尼效果，穿越频率增加，快速性变好，因此B在一定范围内增加可抑制扰动对系统稳定性的影响。综上选取B=10。

L增大时，Nyquist 曲线逐渐远离点（-1，0），说明L增大系统稳定性增强，L=7 mH 和L=10 mH 时的Nyquist 曲线跨度较小。Bode 图中L从1 mH 增加到10 mH，开环传递函数幅值裕度从66.5 dB 增加到82.9 dB，系统稳定性增强；穿越频率从955 rad／s 减小至778 rad／s，减小幅度有限，对快速性影响微弱。综上选取L=7 mH。

综上，J、B、L选取合适数值时，能够使VDCM 控制策略具有较好的幅值裕量和穿越频率，有效提升直流微电网稳定性及快速性。

4 仿真分析与实验验证

在MATLAB／Simulink 中构建附录A 图A6所示孤岛模式下直流微电网仿真模型，其中光伏模块采用最大功率点跟踪控制，储能单元分别采用P-U下垂控制和所提新型VDCM 控制，仿真参数见附录A表A2。

4.1 改进前、后仿真对比

工况1：光伏输出功率恒定为5 kW，图5（a）为负载功率pload波动时udc输出波形图。0.8 s 时负载功率从4 670 W 减小至2 140 W，可看出负载功率突降瞬间，相比P-U下垂控制，采用改进VDCM 控制udc上升超调量减小8.1 V，且恢复至稳态后减小0.6 V；1.2 s时负载功率由2 140 W 增大至5 610 W，突升瞬间采用改进VDCM 控制的udc下降超调量减小9 V，且恢复至稳态后减小0.2 V，更趋于额定值。同时，由图5（b）可看出，负载功率波动时，所提VDCM 控制下idc能够更快上升／下降至所需值。

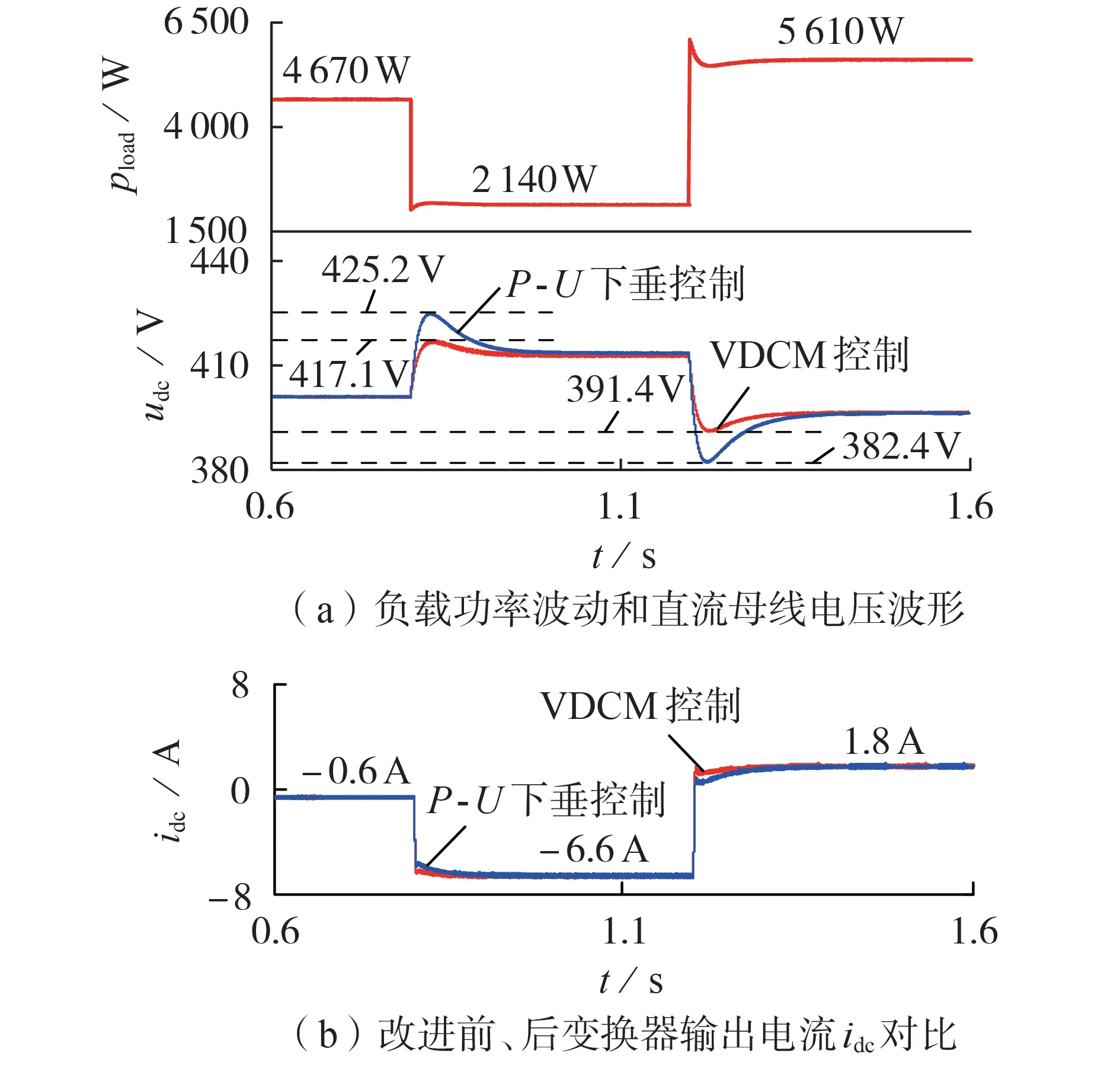
图5 负载功率波动时仿真波形Fig.5 Simulative waveforms of load power fluctuation

工况2：设置负载功率恒定，图6 为光伏功率pPV波动时的仿真波形图。0.8 s 时光伏功率从5 000 W升高至6550 W，由图6（a）可看出光伏功率突升瞬间，改进前udc上升超调量减小4.1 V，恢复至稳态后的误差减小0.5 V；1.2 s 时光伏功率由6 550 W 减小至2 350 W，突降瞬间改进VDCM 控制下的udc超调量相比减小10.3 V，恢复至稳态后的误差减小0.6 V，更趋于额定值。图6（b）中，光伏功率波动时，所提VDCM控制下idc能够更快上升／下降至所需值。

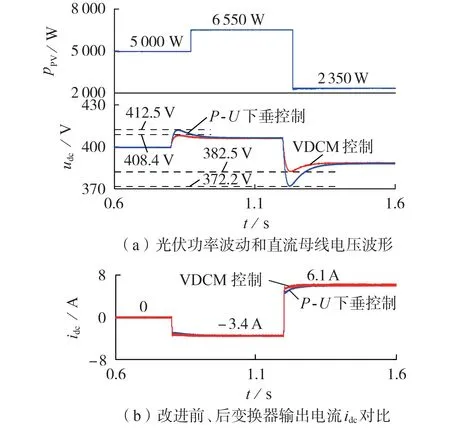
图6 光伏功率波动时仿真波形Fig.6 Simulative waveforms of PV power fluctuation

4.2 实验验证

为进一步验证所提VDCM 控制策略有效性，搭建附录A 图A7所示的直流微电网实验平台，参数见附录A表A2，模拟了负载波动和光伏波动2种工况。

图7（a）、（b）分别为负载功率波动时采用P-U下垂控制和新型VDCM 控制得到的实验波形。令光伏输出电流iPV恒定为12 A，负载功率突增瞬间，改进前、后udc分别跌落8.8 V 和6.3 V，改进后跌落幅值更小；恢复至稳态后udc分别为394.7 V和395.0 V，改进后更接近额定值；蓄电池输出电流ib由1.2 A 升高至9.6 A，改进后为直流侧提供更多能量。

图8（a）、（b）分别为光伏输出电流波动时采用P-U下垂控制和VDCM 控制得到的实验波形。维持负载功率恒定，光伏输出电流iPV由7.1 A 升高至11 A，改进前、后udc分别上升6.9 V 和5.1 V，改进后上升幅值减小；恢复至稳态后udc分别为392.3 V 和392.5 V，改进后更接近额定值；蓄电池输出电流ib由23.7 A 减小至12.1 A，改进后向直流侧提供的能量减少。

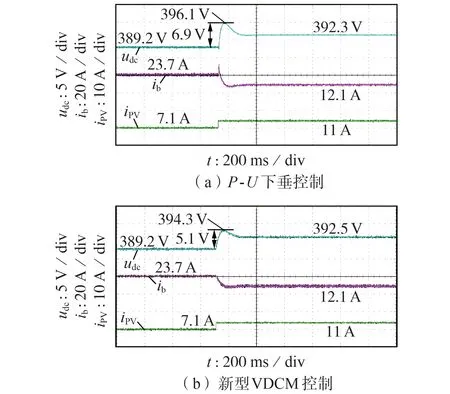
图8 光伏功率波动下实验波形Fig.8 Experimental waveforms under PV power fluctuation

综上所述，所提VDCM 控制策略相比P-U下垂控制能够在负载功率和光伏输出电流波动瞬间降低udc超调量，能够快速达到稳态并减小稳态误差，增强直流微电网的动态调节和惯性阻尼特性。

5 结论

本文针对传统VDCM 控制策略未考虑直流电机转速动态调节问题，模拟了直流电机定转子绕组间的电磁感应作用，提出了一种应用于储能侧双向DC／DC 变换器的新型VDCM 控制策略。所提策略可主动为低惯性的电力电子变换器引入惯量和阻尼以提高惯性和阻尼特性，相比已有的VDCM 控制策略结构更为简单。同时，能够增强直流微电网的动态调节能力，减小直流侧功率变化时的电压超调量，有效提升直流微电网运行稳定性，仿真和实验结果验证了所提策略的有效性和优越性。

附录见本刊网络版（http：//www.epae.cn）。