基于能量回馈的电力电子变压器软启动策略

聂川杰，熊 飞，陈晓雷，邓钦元，严 冬

（重庆邮电大学 自动化学院，重庆 400065）

0 引言

电力电子变压器PET（Power Electronic Trans⁃former）一般由交流网侧AC／DC 变换器和高频隔离型DC／DC变换器两部分组成［1］。基于级联H桥CHB（Cascaded H-Bridge）和双有源桥DAB（Dual Active Bridge）变换器的PET是最为广泛研究的一种拓扑结构［2⁃3］。PET 在高压直流输电［4］、可再生能源发电并网系统［5］、电能路由器［6］、牵引变压器［7］、电池储能系统［8］等领域都有着广阔的应用前景。

PET 拓扑结构中存在大量的电容器组，在未启动时这些电容的初始储能都为0。在AC／DC 侧，未充电的电容在PET 刚并网时相当于将电网短路，会产生较大的冲击电流，威胁到装置和元器件的安全。在DC／DC 侧，未充电的电容电压等于0，隔离型DC／DC 变换器高、低压直流侧电压初始差别较大，启动初期容易导致器件过流。因此，国内外学者针对各种PET 拓扑结构的软启动策略，已经开展了广泛研究并取得了一些成果［9⁃13］。

针对CHB 的软启动，在启动初期阶段直流侧电压还未建立而且CHB 处于不可控整流状态。在CHB与电网之间串联启动电阻以达到有效限制并网初期的冲击电流的目的是常见的做法［9⁃13］。然而这些文献未对启动电阻大小与网侧冲击电流之间的定量关系进行分析，不能够对启动电阻进行理论上的优化设计。在不可控整流阶段结束后，文献［12⁃13］令CHB 直接进入闭环控制将直流电压快速提升到参考值。然而不可控整流阶段结束时的直流电压与其参考值之间仍然存在较大差距，直接令CHB 进入闭环控制将会导致较大的并网冲击电流，如文献［12］中的冲击电流达到了额定值的10 倍，这将严重威胁器件的工作安全。文献［13］则指出可采取2 套不同的CHB 闭环控制参数，一套用于正常闭环工作，另一套则专门用于软启动阶段，以便在快速启动与冲击电流之间实现妥协，然而在2 套参数之间切换既增加了控制的复杂性，又增加了参数设计的复杂性。文献［14⁃15］引入了斜坡的机制，令闭环控制的电压或电流参考值进行斜坡式地缓慢增加，从而延长启动时间，降低启动过程的平均功率，最终达到削减冲击电流大小的目的。然而斜坡斜率往往依赖经验进行设计，若斜率过小则启动时间太长，若斜率过大则达不到限流的效果。

针对DAB 的软启动，文献［12］将DAB 高、低压直流侧电压之间的差值控制到0，实现两侧直流电压的同步上升。然而此方法没有直接针对DAB 的电流进行控制，电流大小由CHB 输入功率和DAB 的控制参数共同决定。当CHB 输入功率较大且DAB的响应速度较快时，DAB 仍然可能会出现过流的情况。文献［13］建立了DAB 在启动过程中的电流应力模型，通过此模型设计了DAB 移相比斜坡变化的斜率以确保在启动过程中DAB 不会过流。然而此方法仍然属于斜坡式的软启动方法，DAB 的电流峰值在绝大多数时都小于其限值，此类方法不能最大化利用变换器的功率传输能力。不仅如此，文献［13］与文献［12］相似，在软启动最后阶段都是CHB的直接闭环控制，输入功率的突然增加仍可能导致DAB出现过流的情况。

针对上述问题，本文提出了一种基于能量回馈的PET 软启动策略。首先针对不可控整流阶段，本文推导了冲击电流和启动电阻之间的数学关系，实现了启动电阻的定量优化设计。然后针对DAB 的软启动，提出了DAB 在2 种工作模式下的峰值电流控制方法。建立了各变换器峰值电流的数学模型，同时兼顾交流侧和直流侧的电流限制需求。接着针对CHB 的软启动，提出了能量回馈的方法。利用DAB双向功率传输的特性以及器件电压耐受能力的充足裕量，将低压直流侧电容适度过充并将其中部分能量再回馈到高压侧，以缩小高低压侧直流电压的差距。在本文提出的软启动方法中，DAB 始终处于峰值电流的控制模式下，以实时挖掘其当前允许的最大功率传输能力，提高了软启动速度。CHB 全程处于不可控整流模式，在软启动结束以及CHB 即将进入闭环控制前其高压侧直流电压就已达到参考值，从而彻底消除交流侧的冲击电流。不仅如此，在软启动全过程中各变换器电流峰值都能够被定量地计算和控制，真正实现了安全可靠的软启动。本文提出的方法避免了繁琐的斜坡斜率和控制器参数的设计过程，完全依靠理论模型而不是经验来指导软启动过程的设计。最后，通过仿真与实验验证了所提软启动策略的正确性和有效性。

1 PET的拓扑结构与数学模型

1.1 拓扑结构

本文针对图1 所示的单相N级PET 进行研究，输入级为CHB，隔离级为DAB。在电网侧，e为电网电压，Ls为并网电感，is为PET 的并网电流，R为启动电阻，K1和K2为断路器，vi（i=1，2，…，N）为第i级H桥的交流输出电压；在高压直流侧，CH，i为第i级高压直流母线电容，vH，i为第i级高压直流母线电压；在低压直流侧，各级DAB 的输出端并联，CL，i为第i级低压直流母线电容，vo为低压直流母线电压，Lr，i为第i级高频变压器T 的漏感与辅助电感之和，io为PET 的直流侧负载电流，iLr，i为第i级电感电流。

图1 PET拓扑结构Fig.1 Topology of PET

DAB 的拓扑结构见附录A 图A1（a），开关器件Q1—Q4组成DAB 的原边全桥，Q5—Q8组成DAB 的副边全桥。原边全桥内移相比指Q1和Q3驱动脉冲移相时间与DAB 半个开关周期的比值，外移相比指Q1和Q5驱动脉冲移相时间与DAB 半个开关周期的比值。

1.2 数学模型

假设各级高、低压直流母线电容参数相同，各DAB高频变压器的漏感参数相同，即：

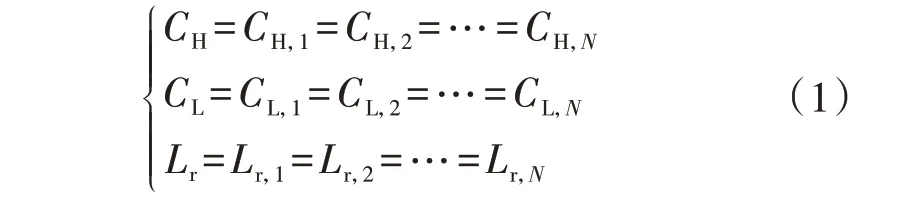
CHB的数学模型可以表示为：

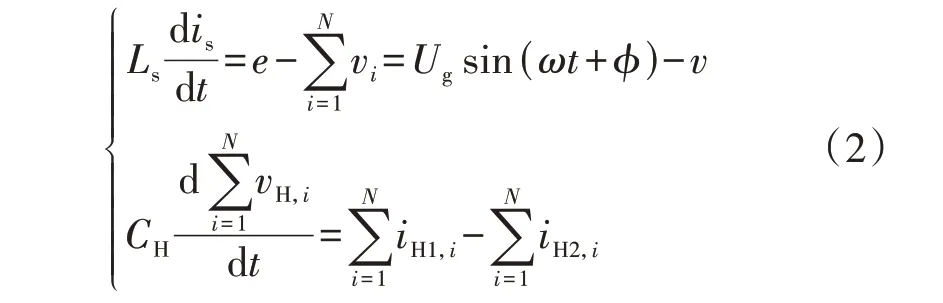
式中：v为CHB 交流输出电压；Ug为电网电压峰值；ϕ为电网电压初相角；ω为电网电压角频率；iH1，i为第i级高压直流侧电流；iH2，i为第i级DAB输入电流。

以单移相为例，第i个DAB的传输功率PDAB，i为：

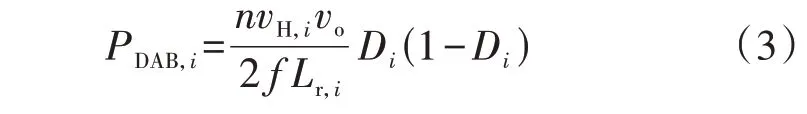
式中：f为DAB 的开关频率；n为高频变压器的变比；Di为第i级DAB的外移相比。

1.3 PET的传统软启动策略

传统的软启动策略一共分为如下3个阶段［12⁃13］。

1）第1 阶段，K1闭合，K2断开，串联启动电阻，所有开关器件闭锁，CHB 不可控整流建立高压直流母线电压。

2）第2 阶段，K1断开，K2闭合，切除启动电阻，DAB 副边开关器件闭锁，原边全桥内移相比斜坡增加，此阶段DAB 的拓扑结构见附录A 图A1（b）。斜坡的斜率一般按照经验加上适度的裕量来进行设计，往往导致启动时间过长，还不能充分利用DAB的功率传输能力，启动的快速性难以满足。

3）第3 阶段，所有开关器件使能工作。CHB 与DAB 从第2 阶段直接进入闭环控制，分别将高、低压直流母线电压进一步提升到参考值，高压直流母线电压均衡控制使能，并且由DAB 完成［12⁃13，16⁃17］。由于在第2 阶段结束后，高、低压直流母线电压都未达到参考值，直接切入闭环控制仍将引起较大的冲击电流。

2 基于能量回馈的PET软启动策略

为了解决上述问题，本文提出一种新型的PET软启动方法，具体如下。

1）第1 阶段。与传统软启动策略相同，CHB 为不可控整流。本文通过对启动电阻的优化设计，在限制网侧冲击电流的情况下有效缩短此阶段时间。

2）第2 阶段。DAB 原边全桥使能工作，副边全桥闭锁，令DAB 工作于最大峰值电流模式给低压直流母线电容充电。

3）第3 阶段。①第3a 阶段，利用器件电压耐受能力的充足裕量（最高耐压一般在额定电压的2 倍以上），将低压直流母线电容视作储能单元，允许其在CHB 并网之前多储存一部分能量。在此阶段中，DAB 原、副边全桥全部使能工作，令DAB 仍然工作于最大峰值电流模式给低压直流母线电容过充电。②第3b 阶段，将低压直流母线电容中过充的多余能量回馈到高压直流母线电容中，使得高压直流母线电压达到或尽可能接近其参考值，从而消除CHB 在并网瞬间的冲击电流。

2.1 第1阶段

CHB 处于二极管不可控整流状态，DAB 原边和副边全桥均处于闭锁状态。为了限制网侧冲击电流，一般需在PET 与电网间串联一个启动电阻。若启动电阻过小则网侧冲击电流较大，虽然能大幅缩短第1 阶段的启动时间，但是可能损坏器件；若启动电阻过大，则能有效限制网侧冲击电流，但是启动时间将会显著增加，难以满足快速启动的需求。

对于N级CHB，高压直流侧相当于N个电容串联，则等效后的电容为C=CH/N。仅考虑电网正半周的情况，有：

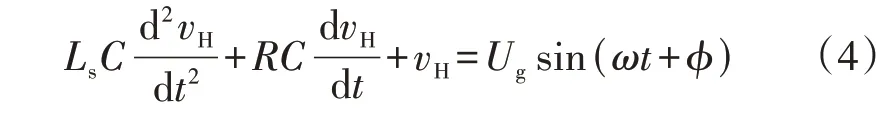
式中：vH=vH，1=…=vH，N。

一般串联的启动电阻较大，因此忽略欠阻尼和临界阻尼情况。求解式（4）可得：

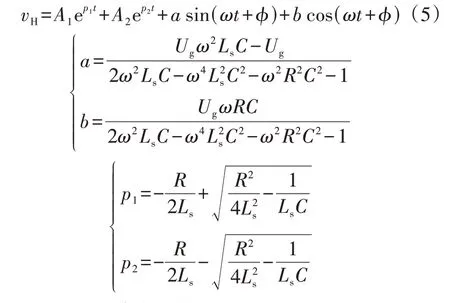
式中：A1和A2为待定系数。

在电网电压的第1 个半周期内，网侧电流最大，因此只需要限制网侧电流在第1 个半周期内的峰值小于其最大允许值即可。为了简化分析，假设电网电压的初相角ϕ=π/2（因为此时网侧电流最大，为最恶劣工况）。电容初始电压为vH=0，电感初始电流为is=0，代入式（5）可得：

对式（5）求导可得is与R的关系为：

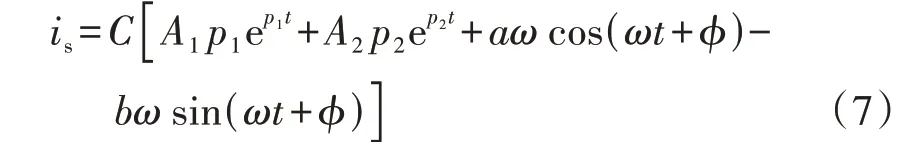
根据式（7）和附录A 表A1 所示的实验参数，绘制在第1 个电网周期内is的最大启动冲击电流is，max与R的关系曲线，如图2 所示。根据开关器件的过流能力，人为选择is，max值，根据图2 得出最小启动电阻。本文选择点B，启动电阻为22 Ω，最大启动冲击电流为14.81 A。

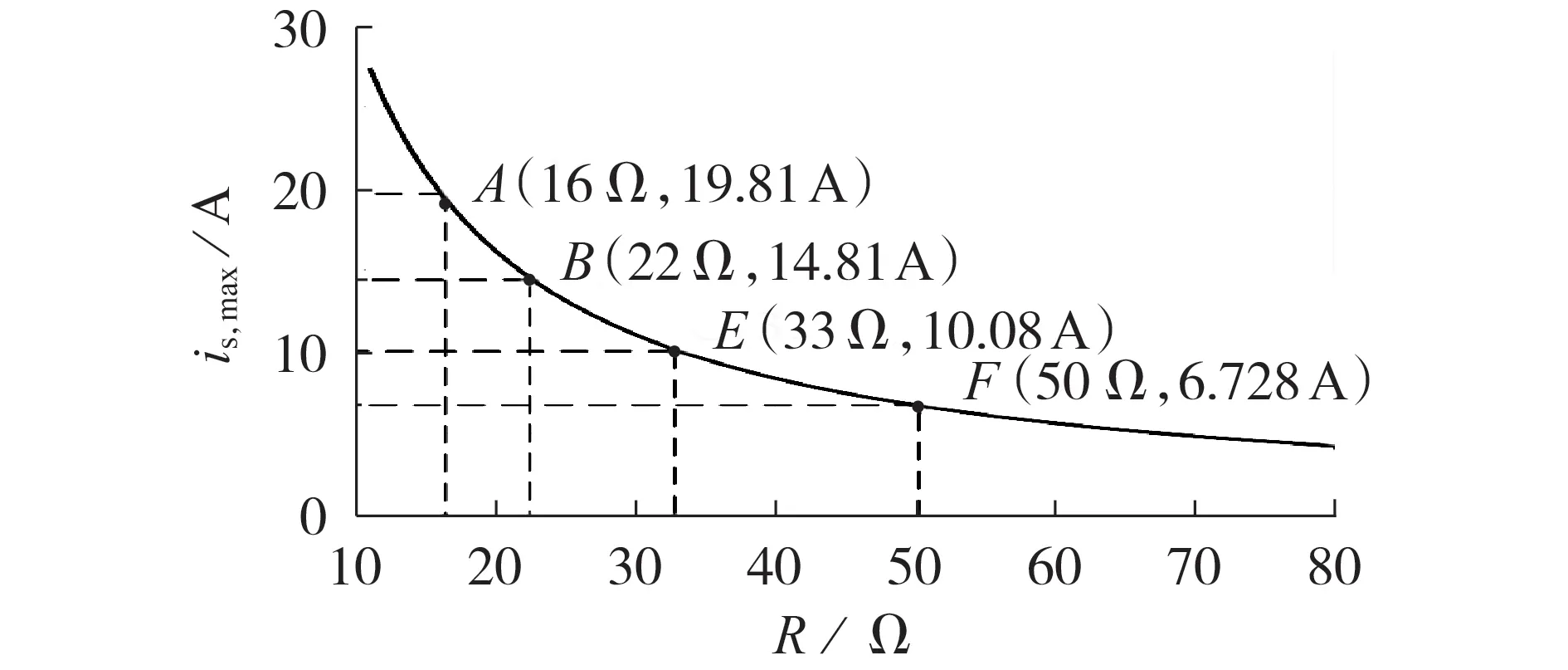
图2 最大启动冲击电流与启动电阻的关系Fig.2 Relationship between maximum starting impulse current and starting resistance

第1 阶段结束后，高压直流母线电压vH≈Ug/N，低压直流母线电压vo≈0。

2.2 第2阶段

在第2 阶段中，DAB 原边全桥工作，副边全桥闭锁，CHB 仍处于不可控整流状态。DAB 工作于不连续模式DCM（Discontinuous Conduction Mode）或连续模式CCM（Continuous Conduction Mode），如附录A图A2所示［18］。

DCM与CCM的边界βdcm，ccm为［19］：

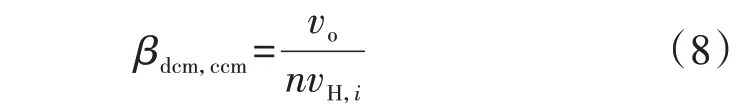
当原边全桥内移相比ββdcm，ccm时，DAB 工作于DCM，电感峰值电流ipeak，dcm和传输功率Pdcm分别为：

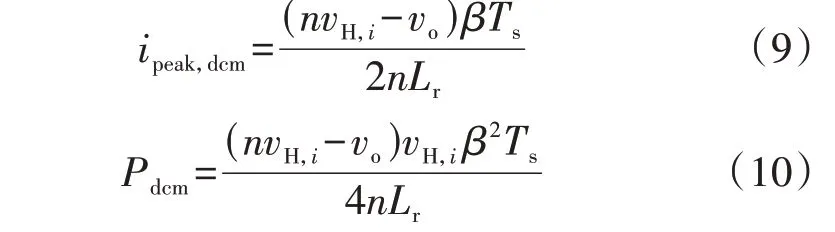
式中：Ts为DAB的开关周期，且Ts=1/f。

当β≥βdcm，ccm时，DAB 工作于CCM，电感峰值电流ipeak，ccm和传输功率Pccm分别为：

根据式（9）、（11）分别求解出在电感峰值电流iLr，peak，2限制下DCM 的最大允许内移相比βmax，dcm，1与CCM的最大允许内移相比βmax，ccm，1为：

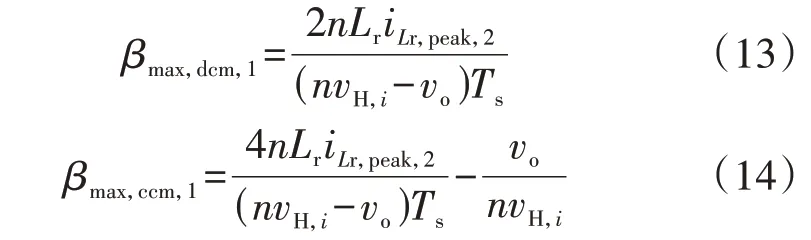
可以看出：当βmax，dcm，1βdcm，ccm时，βmax，ccm，1βdcm，ccm也成立，此时DAB 工作于DCM；当βmax，dcm，1>βdcm，ccm时，βmax，ccm，1>βdcm，ccm也成立，此时DAB 工作于CCM。因此DAB 工作模式具有唯一性。在第2 阶段中，实时 计 算βdcm，ccm、βmax，ccm，1和βmax，dcm，1来 判 断DAB 处 于DCM 还是CCM，并分别选择式（13）或式（14）进行计算。

2.3 第3阶段

在第3 阶段中，DAB 原、副边全桥都使能工作，高压直流母线电压均衡控制由DAB 完成，CHB 仍处于不可控整流状态。

2.3.1 第3a阶段（能量过充）

以某一级的电容为例进行分析，设高压直流母线电压从第3 阶段的初始值提升到参考值vH，ref所需要补充的能量EH为：

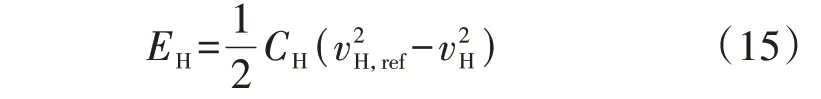
低压直流母线电容过充能够储存的多余能量EL为：

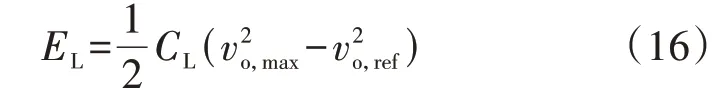
式中：vo，max为期望的低压直流母线电压的过充最大值；vo，ref为低压直流母线电压的参考值。

若令EH全部由低压直流母线电容能量回馈得到，即EH=EL，则可得vo，max为：

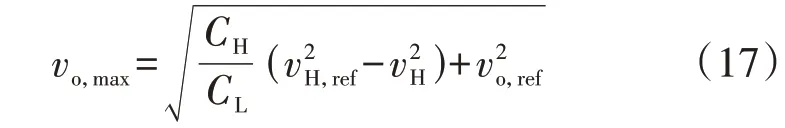
可以看出，vo，max与高、低压直流母线电容的比值相关。

在第3a 阶段中，高压直流母线电压vH受CHB 不可控整流的充电影响而基本保持恒定，DAB原、副边全桥的内移相比都为最大值1，DAB 采用单移相调制方法。DAB 继续按照峰值电流模式工作，将低压直流母线电容电压过充到vo，max。此时电感峰值电流iLr，peak，3a为（以某一级DAB 为例进行分析时，Di简写为D）：

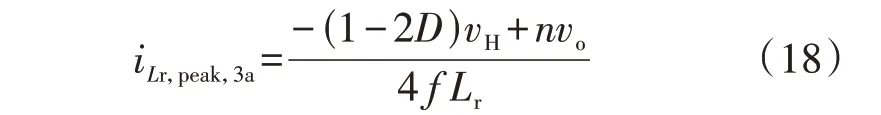
因此，在保证DAB 不过流的情况下，可得最大允许外移相比Dmax，3a，1为：

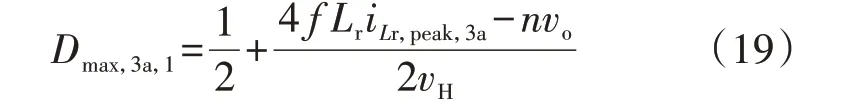
在理想情况下，低压直流母线电压vo可以被过充到期望值vo，max。然而，由于受到单移相控制在两侧直流母线电压不匹配情况下传输的无功功率过高和低压直流母线电容容量不足的双重限制，式（17）的期望值vo，max将可能无法达到。在式（18）中，当iLr，peak，3a和vH都一定时，vo越大，则D越小。特别地，当nvo=4f LriLr，peak，3a+vH时，D恰好等于0。此时，DAB 在电感峰值电流已达到最大允许值的情况下，只能传输无功功率而无法继续给低压直流母线电容充电。

因此，受无功功率传输的影响，当DAB 电感峰值电流的限制已确定时，低压直流母线电压将存在一个固有的最大值vo，max，lim，具体为：

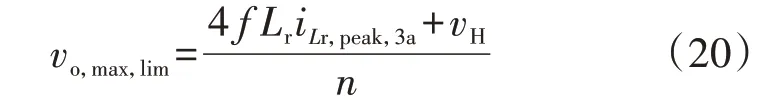
式（20）表明DAB在电感峰值电流限值为iLr，peak，3a时最多能给低压直流母线电压充至vo，max，lim。然而，式（17）给出了期望的低压直流母线电容过充电压为vo，max。因此，只有当vo，max，lim≥vo，max时，第3阶段的软启动过程才能够达到理想的情况。下面分2 种情况进行讨论。

1）当vo，max，lim≥vo，max时，可以通过DAB 将低压直流母线电压过充到vo，max，此时可以达到理想条件，高压直流母线电压将提升到参考值。

2）当vo，max，limvo，max时，不能通过DAB 将低压直流母线电压过充到vo，max。为了解决这个问题，可以有2 种思路：①根据式（17）可知，在设计阶段就适当增加低压直流母线电容的容量以减小vo，max；②根据式（20）可知，可以选择耐受电流能力更大的器件，从而增大电感峰值电流的限制以提升vo，max，lim。

实际上，除了PET 自身的低压直流母线电容器组以外，在多数应用场合中PET 的低压直流母线上还会挂载很多变换器作为负载［19⁃20］，而这些负载级的变换器也将提供直流电容。在这种情况下，PET低压直流母线电容容量将比其高压直流母线电容容量大得多，完全可以被利用作为储能单元，此时vo，max，lim≥vo，max的理想条件也容易被满足。即使达不到理想条件（低压直流母线电容量不足，能量回馈不足），本文所提出的能量回馈策略也能够使高压直流母线电压vH上升，以减小vH与vH，ref之间的差距，从而达到削减CHB并网冲击电流的目的。

2.3.2 第3b阶段（能量回馈）

当低压直流母线电压vo达到vo，max时，DAB 以开环控制的方式反向传输功率，将低压直流母线电容能量回馈到高压直流母线电容中，最终使高、低压直流母线电压均达到参考值（理想条件）或仅低压直流母线电压达到参考值而高压直流母线电压与参考值的差距缩小（非理想条件）。

在能量回馈的过程中，DAB仍然是原、副边全桥都使能工作，此时电感峰值电流iLr，peak，3b为：

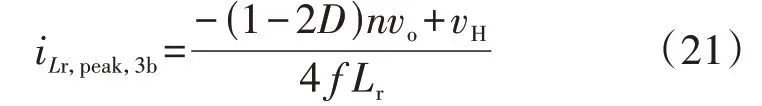
此时，在保证DAB 不过流情况下，最大外移相比Dmax，3b为：

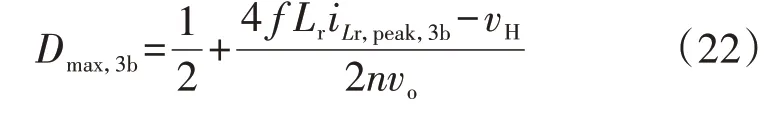
在理想情况（不考虑功率损耗）下，由式（15）—（17）可知，当高压直流母线电压恰好达到参考值时，低压直流母线电压也恰好达到其参考值。然后CHB与DAB 可以直接进入闭环控制，将不再产生冲击电流，PET软启动完成。

2.4 CHB和DAB的电感峰值电流共同限制方法

在软启动过程中，CHB 一直处于不可控整流的被动状态。若DAB 按照式（13）、（14）、（19）进行控制，则只能保证DAB 自身的电感峰值电流不会超过限值，却无法确保网侧电流不过流。因此需要同时对直流侧DAB电流与交流侧电网电流进行限幅。

在CHB 不可控整流情况下，高压直流母线电压、电网电压和电网电流在半个电网周期内的波形如图3所示。

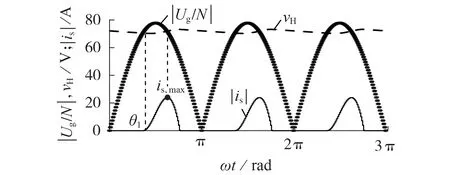
图3 高压直流母线电压、电网电压和电网电流波形Fig.3 Waveforms of high-voltage DC bus voltage，grid voltage and grid current

由图3 可见，高压直流母线电压vH的二倍频100 Hz 波动分量幅度远小于其平均值。因此，vH的二倍频波动可以被忽略。由二极管不可控整流电路的工作特性可知，vH的平均值与其负载功率大小紧密相关。在本文的PET 中，vH的平均值是关于DAB从高压侧吸收的平均功率PDAB的函数。此时交流侧电网电流可通过式（23）求解得到。

式中：ωt∈（θ1，π-θ1），θ1=arcsin（NvH/Ug）。

根据式（23）可知，当ωt=π-θ1时，交流侧电网电流取得最大值is，max，具体为：

可以看出，is，max是关于vH的一元函数。式（24）是一个关于vH的超越方程，当is，max的最大允许值确定时，借助MATLAB 可以离线求解在交流侧电网电流峰值恰好等于限值时的高压直流母线电压最小允许值vH，min。然后，将vH，min作为已知量代入式（23）中，则is转化为关于ωt的一元函数。此时，CHB 在半个电网周期内从电网吸收的平均功率PAC，max为：

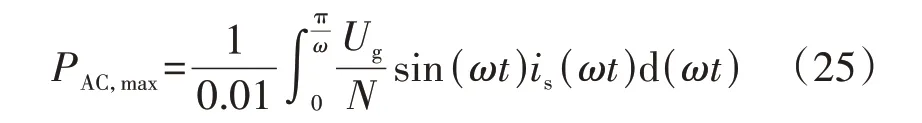
根据能量守恒定律可得，PAC，max≈PDAB（忽略vH的二倍频波动）。将PAC，max分别代入式（3）、（10）、（12）中，可求得DAB最大允许移相比如下。

第3a阶段DAB最大允许外移相比Dmax，3a，2为：

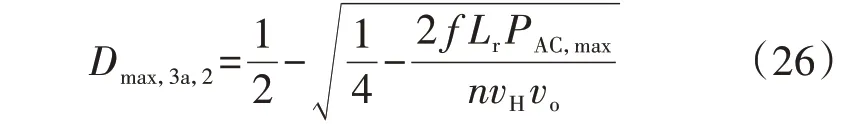
第2 阶段DAB 在DCM 下最大允许内移相比βmax，dcm，2和CCM下最大允许内移相比βmax，ccm，2分别为：

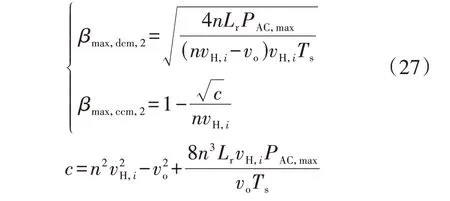
值得注意的是，式（25）中的PAC，max是通过离线计算得到的，是一个常数。而式（26）中的Dmax，3a，2、式（27）中的βmax，ccm，2和βmax，dcm，2则是由控制器根据实时的vH和vo在线计算得到的。因此，这几乎不会增加控制器的计算负担。

最后，为了同时满足交流侧电网电流限制与DAB 电感峰值电流限制，在第2 阶段应选择式（13）或式（14）与式（27）中较小的一个内移相比作为最终的控制变量，即：

在第3a 阶段应选择式（19）与式（26）中较小的一个移相比作为最终的控制变量，即：

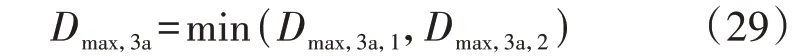
综上所述，本文所提PET 软启动整体流程见附录A图A3。

3 仿真与实验验证

3.1 仿真验证

为了体现不同低压直流母线电容情况下并网冲击电流的削减程度，搭建了仿真模型。仿真中，高压直流母线电容始终设置为1.6 mF，低压直流母线电容取值见表1，其余参数见附录A 表A1。根据式（20）计算可知：当DAB 电感峰值电流限制设置为7.5 A 时，vo，max，lim=117 V。根据式（16）计算可知，当低压直流母线电容CL>1.7 mF时，即可达到理想条件。

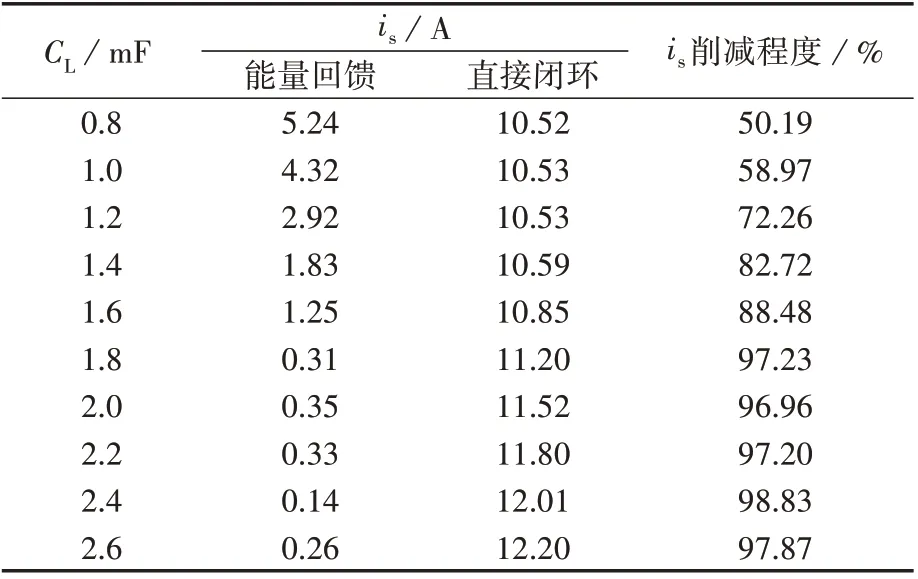
表1 不同低压直流母线电容下并网冲击电流仿真结果Table 1 Simulative results of grid-side impact current under different low voltage DC bus capacitors

从表1 可以看出：当低压直流母线电容较小，能量回馈不足时，能量回馈策略能有效削减并网冲击电流；当低压直流母线电容足够大时，能量回馈策略几乎能完全消除并网冲击电流。原因有以下2 点：①能量回馈策略有效减小了高压直流母线电压与参考值的差距；②能量回馈后，低压直流母线电压已经达到参考值，在进入闭环控制时，DAB将不会再从高压侧吸收能量，使CHB 从电网吸收的能量更少，进一步减小了并网冲击电流。

3.2 实验验证

为验证本文所提PET软启动策略的合理性与可行性，搭建了以TMS320F28335 和10M50SAE144I7G为核心控制器的2 kW 四级联实验样机，见附录A 图A4。高压直流母线电容为1.6 mF，低压直流母线电容为3.2 mF，其余参数见附录A表A1。

针对图2中的4个取值点A、B、E、F，实验波形见附录A 图A5。对比点A、B、E、F对应的高压直流母线电压vH曲线可以看出，启动电阻阻值越大，虽然限制冲击电流越明显，但是也会导致vH增长缓慢，软启动第1 阶段时间将被延长。实验结果与图2 的理论结果一致。

图4 为传统软启动策略（斜坡式）［12⁃13］下第2、3阶段的实验波形。图中：vab为DAB 原边全桥的方波电压；vcd为DAB 副边全桥的方波电压。第2阶段内，DAB 原边全桥内移相比从0 到1 斜坡增加。经过反复尝试以后选择特定的斜率使得DAB 电感峰值电流为7.5 A，此阶段持续时间约为56 ms；第3阶段内，CHB 与DAB 直接切入闭环控制，此时交流侧冲击电流约为24 A，选择合适的控制参数使DAB 电感峰值电流仍为7.5 A，第3 阶段持续时间约为104 ms。由图4可见，第3阶段直接切入闭环控制将会导致交流侧出现较大的并网冲击电流。

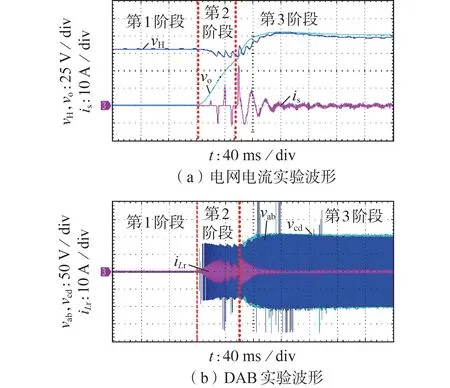
图4 传统软启动策略第2、3阶段的实验波形Fig.4 Experimental waveforms of Stage 2 and 3 under traditional soft start strategy

本文所提软启动策略的实验波形如图5 所示，其细节放大图见附录A 图A6。为了满足理想条件，根据式（17）计算可知，vo，max=108 V。因此，在实验中，考虑到能量传输的损耗，设置vo，max为110 V，略高于108 V。设置iLr，peak，2=iLr，peak，3a=iLr，peak，3b=7.5 A（与图4的传统软启动策略相同），is，max=15 A，根据式（23）—（25）进行离线计算可得PAC，max=223 W。

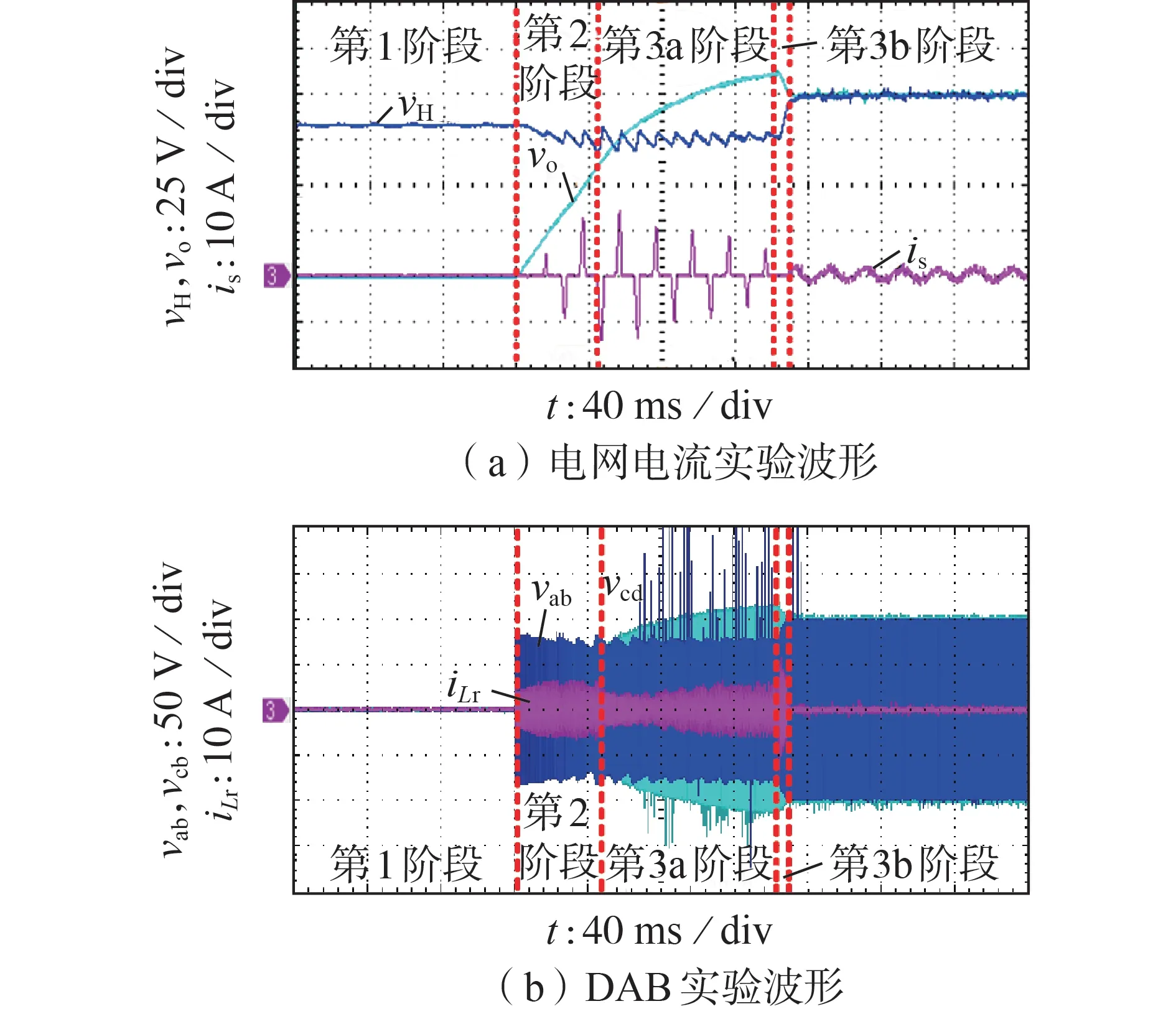
图5 本文所提软启动策略第2、3阶段的实验波形Fig.5 Experimental waveforms of Stage 2 and 3 under proposed soft start strategy

在第2 阶段内，DAB 原边全桥内移相比按照式（28）变化，此阶段持续时间约为48 ms。相比于传统软启动策略，本文所提软启动策略在第2 阶段的持续时间减少了14.29%。

在第3a 阶段内，DAB 按照式（29）对低压直流母线电容充电，此阶段持续时间约为96 ms。在第3b阶段内，DAB 按照式（22）将能量从低压直流母线电容回馈到高压直流母线电容中，此阶段持续时间约为4 ms。因此，第3 阶段总耗时约为100 ms。在第3b 阶段结束时，高、低压直流母线电压均达到参考值，CHB 与DAB 同时切入闭环控制，并网时刻的冲击电流约为0，PET 整体启动完成。可以看出，在整个软启动阶段，交流侧并网冲击电流峰值被限制在15 A以内，DAB电感峰值电流被限制在7.5 A以内。

从启动时间来看，本文所提软启动策略相比传统软启动策略略有提升；从对电流限幅的方法来看，传统软启动策略高度依赖对控制参数和斜坡斜率等因素的设计来限制并网冲击电流，而本文所提软启动策略直接基于数学模型实时计算控制量以达到限制并网冲击电流和快速启动的双重目的；从对软启动过程设计的复杂性来看，传统软启动策略需要大量仿真模拟以及经验来设计关键控制参数和斜坡斜率，还要考虑CHB 和DAB 动态性能上的配合问题，本文所提软启动策略则没有参数设计过程，完全基于数学模型进行控制；从对电流限幅的效果来看，传统软启动策略无法消除并网冲击电流，无法直接对各部分变换器的电感峰值电流进行控制，而且需要在启动快速性和限制冲击电流之间做出权衡，本文所提软启动策略能够消除并网冲击电流，而且实时控制交、直流侧峰值电流，不仅严格限制了交、直流侧峰值电流，还充分利用了DAB 的最大功率传输能力。

4 结论

针对PET 在启动过程产生并网冲击电流的问题，本文提出了一种基于能量回馈的PET 软启动策略，根据理论分析和实验结果可得如下结论。

1）传统软启动策略在各个启动阶段将出现较大的并网冲击电流；本文所提软启动策略在整个软启动阶段都是基于数学模型进行控制，交流侧并网冲击电流与DAB 电流应力都能被严格地限定在设定值内。

2）传统软启动策略在启动阶段出现的并网冲击电流大小与控制参数、斜坡斜率等因素有关，为了限制并网冲击电流幅值，需谨慎设计控制参数；本文所提软启动策略下，在整个软启动阶段CHB 与DAB 都未进入闭环控制，全程基于数学模型控制而无需进行复杂的参数设计。

3）在CHB 由不可控整流模式切入脉宽调制整流模式时，传统软启动策略将会出现较大的并网冲击电流；本文所提软启动策略能够消除PET 并网瞬间产生的冲击电流。

附录见本刊网络版（http：//www.epae.cn）。