基于分布式拟牛顿法的交流微电网经济运行控制

魏珊珊，高 飞，俞嘉浩，蔡位焜，刘 东

（1. 上海交通大学 电力传输与功率变换控制教育部重点实验室，上海 200240；2. 上海交通大学 电子信息与电气工程学院，上海 200240；3. 上海空间电源研究所，上海 200240）

0 引言

近年来，随着人们对能源消耗和环境治理两方面的持续关注，风能、太阳能等可再生能源的渗透率快速提升，能源结构发生巨大改变［1］。然而，可再生能源固有的随机性和间歇性特点给电网的安全稳定运行和电能质量带来了不利影响［2］。微电网作为一种小型供电系统，由分布式电源DG（Distributed Generator）、储能系统、负荷、控制保护设备等基本单元构成，能有效实现可再生能源的友好接入电网［3］。由于DG 的发电成本各异，如何将微电网功率分配与经济运行相结合，以节约发电成本，是微电网能源管理的一个重要问题。

微电网经济运行问题是使系统满足功率供需平衡以及DG 出力约束条件下，总发电成本最小化的问题［4］。目前，微电网的经济运行控制主要基于分层控制，分层控制由一次控制、二次控制和三次控制三部分组成［5］。一次控制基于下垂机制，能有效控制微电网的电压和频率，并且能够在不依赖通信的条件下实现功率按比例分配。对于下垂机制中存在的电压和频率偏差问题，通常利用二次控制在相对较长的时间尺度下解决［6］。三次控制作为分层控制中的最高层，能够在更长的时间尺度下实现能量管理、系统优化和经济调度［7］。然而，由于可再生能源的不确定性和负荷需求的快速变化，电力预测可能存在较大的误差，这使得基于预测的经济调度在微电网中的作用较小［8］，因此，在对微电网的实时电压／频率控制过程中也应该考虑经济优化运行。

微电网中传统的经济优化运行策略大多依赖于集中式控制来实现，通过收集微电网的运行信息，利用通信线和各DG 的本地控制单元进行高带宽的点对点通信，集中式控制的调节准确度高，但是增加了通信和计算成本，此外，集中控制器本身容易导致单点故障，不利于未来微电网的拓展和DG、负荷的“即插即用”［9］。为克服集中式控制的不足，有学者提出基于无通信的自治经济下垂控制。文献［10⁃12］分别考虑DG 发电成本、边际成本和需求侧管理，提出非线性下垂控制，通过优化功率分配来降低微电网的总发电成本。尽管下垂控制简单，但由于缺乏协调，基于下垂控制的经济优化策略仍然存在一些固有的缺点，例如，资源之间的负载共享不是最优的，动态性能差可能导致争用控制［8］，此外，下垂控制对测量误差非常敏感，需高精度的测量。不基于下垂机制的分布式协同控制策略则利用稀疏通信网络与相邻网络交换信息，在某些通信链路故障时也能够保持系统全部功能，克服了集中式控制和下垂控制的缺点［13⁃14］。文献［13］结合等耗量微增率准则和次梯度算法，在实现直流微电网发电成本最小的同时使电压得到恢复。文献［14］利用分布式拟牛顿法控制同步发电机的频率并优化有功功率分配，拟牛顿法利用二阶梯度信息，具有更快的收敛速度，能够实现系统快速收敛，但是该文献没有考虑电压的稳定性以及无功出力带来的间接成本。此外，DG由于输出特性各异，大多以电力电子逆变器为接口并入微电网，这构成了微电网多逆变器环境［15］，需要提出一种针对多逆变器并联微电网的经济运行控制策略。

本文在现有研究的基础上，针对混合电压源型和电流源型逆变器的交流微电网，提出一种分布式经济运行控制策略。该策略利用拟牛顿法优化有功功率和无功功率的分配，并基于改进的下垂控制实现系统发电成本最小和高质量电压／频率控制。首先，介绍交流微电网中逆变器的类型和不同DG 的发电成本，并讨论分布式拟牛顿法的实现过程；然后，介绍基于拟牛顿法的经济运行控制策略；最后，与基于传统下垂控制的经济运行控制策略进行仿真对比分析，验证了本文所提策略能够实现微电网最优的经济运行性能和更优的电压／频率调节性能，并在负荷变化、逆变器故障、通信故障等工况下维持系统稳定运行。

1 交流微电网的发电成本

1.1 交流微电网模型

逆变器是交流微电网中连接DG 和交流母线的重要端口［16］。根据逆变器的运行模式，将其分为组网逆变器、馈网逆变器和撑网逆变器GSI（Grid-Sup⁃porting Inverter）3类［17］。其中：组网逆变器为微电网提供电压和频率的支撑，既可运行在孤岛模式又可运行在并网模式；馈网逆变器可看作理想的电流源，为微电网提供功率；GSI 则是组网逆变器和馈网逆变器的一般形式，其控制框图如图1 所示，包括下垂控制、电压环或功率环、电流环和脉冲宽度调制PWM（Pulse Width Modulation）。根据GSI控制策略的不同，可将其分为电压源型撑网逆变器VS-GSI（Voltage-Source-based Grid-Supporting Inverter）和电流源型撑网逆变器CS-GSI（Current-Source-based Grid-Supporting Inverter）。

图1 撑网逆变器的控制框图Fig.1 Block diagram of GSI control

图1 中：Lf为滤波电感；Cf为滤波电容；rc和Lc分别为线路电阻和电感；ig，abc、io，abc分别为逆变器侧三相电流和网侧三相电流；ug，abc为三相输出电压；ugd、ugq分别为三相电压ug，abc经Park 变换后得到的d、q轴电 压；igd、igq和iod、ioq分 别 为 三 相 电 流ig，abc和io，abc经Park 变换后得到的d、q轴电流；θ为相角；P为逆变器输出的有功功率；Q为逆变器输出的无功功率。VS-GSI 的控制回路包括下垂控制、电压环和电流环，下垂控制用于输出频率的参考值f*和电压的参考值U*，电压环和电流环常采用比例积分PI（Propor⁃tional Integral）控制来控制逆变器的输出电压，为系统提供电压和频率支撑。CS-GSI的控制回路包括下垂控制、功率环和电流环，下垂控制用于输出有功功率的参考值P*和无功功率的参考值Q*，将其除以ugd得到电流的参考值，用于控制逆变器的输出功率及电流。

相较于VS-GSI，CS-GSI 的控制结构较简单，可以减少1个PI控制器。由文献［18］可知，混合VS-GSI和CS-GSI 系统同样可以运行在孤岛模式，实现功率按比例分配。图2 为本文所研究的交流微电网拓扑图。图中：Zline1—Zline6为不同DG 连接交流母线的线路阻抗；DG1—DG3通过VS-GSI 与交流母线相连，为系统提供电压和频率支撑；DG4—DG6通过CS-GSI与交流母线相连，向电网输送功率，参与系统电压和频率的调节。

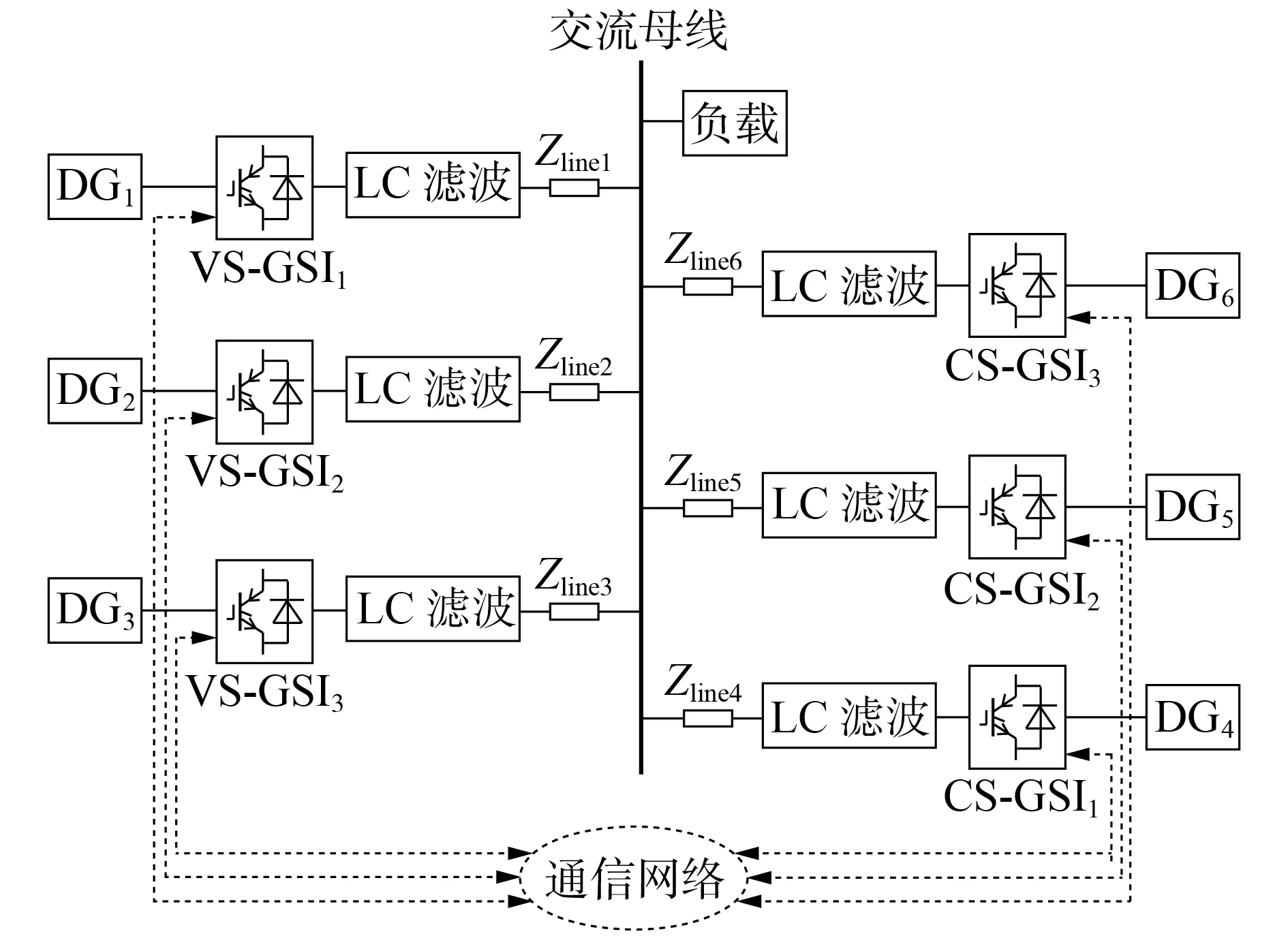
图2 混合VS-GSI和CS-GSI交流微电网的拓扑图Fig.2 Topological diagram of AC microgrid with hybrid VS-GSI and CS-GSI

1.2 有功发电成本

DG 可以分为可调度DG 和不可调度DG。可调度DG 为原动机功率可控制的DG，包括微型燃气轮机、柴油发电机等。不可调度DG 为一次能源具有一定随机波动性的DG，不便于提前调度，包括风电、光伏等。

由附录A 可知，DGi有功发电成本CP，i( )Pi可表示为：

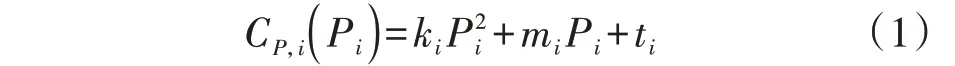
式中：Pi为DGi的有功功率；ki、mi、ti为系数，其值与DGi的类型有关。

1.3 无功发电成本

无功功率的产生不需要直接消耗燃料或其他任何形式的能量，但会导致有功功率损耗［12］，因此，无功发电成本CQ，i(Qi)［10］可以表示为：

式中：Qi为DGi的无功功率；θi为DGi的有功功率损耗占无功功率发电量的比例，根据文献［10］，同步发电机和逆变器的功率损耗分别为其所产生的无功功率发电量的3%和5%。

1.4 优化目标

在微电网经济运行时，系统应满足功率平衡、各DG 出力约束、系统发电成本最小这3 个条件。根据等耗量微增率准则，当各DG 的耗量微增率相等时，负荷分配最优，且系统发电成本最小，因此，优化问题可描述为以下模型：

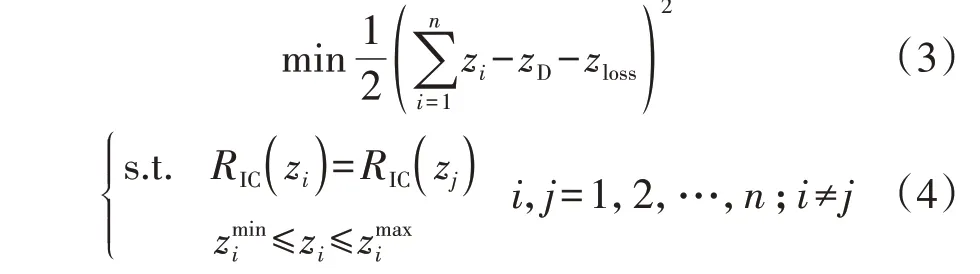
式中：n为微电网中DG 的总数；zi为被控对象（DGi的有功功率Pi、无功功率Qi）；zloss、zD分别为线路损耗和负载功率；RIC( )zi为关于zi的耗量微增率；分别为zi的最小值和最大值。

由式（1）和式（2）可知，DGi有功功率的耗量微增率RIC(Pi)和无功功率的耗量微增率RIC(Qi)分别如式（5）和式（6）所示。

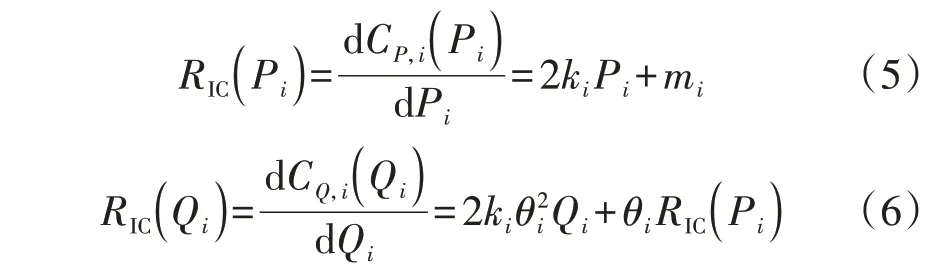
由式（6）可以看出，RIC(Qi)与RIC(Pi)之间存在线性关系，但在式（5）中对RIC(Pi)的优化可独立进行，此外，负荷在某段时间内是固定不变的，因此在对微电网无功发电成本进行优化时，式（6）中的RIC(Pi)可看作常量，其值为有功耗量微增率的稳态值，以此协调有功发电成本最小和无功发电成本最小这2个目标。

为了便于分析，式（5）和式（6）可统一表述为：

式中：当zi表示有功功率时，ai=ki，bi=mi，当zi表示无功功率时，ai=ki，bi=θiRIC(Pi)。令RIC(zi)=RIC(zj)=x，根据式（7），式（3）可以改写为：

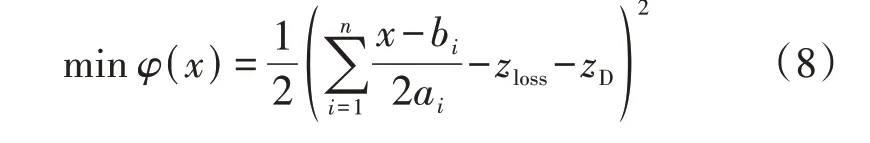
此时，目标函数的直接被控对象为功率的耗量微增率x。值得注意的是，式（8）依然需要满足式（4）的约束条件。根据等耗量微增率准则，当某DG 的输出功率达到某个界限时，应将其固定为最值，并将该DG 称为固定电源。为了保证系统优化更新过程能够继续，固定电源的耗量微增率应继续参与系统的优化更新，但始终保持固定电源的输出功率不变［14］。

2 分布式拟牛顿法

2.1 迭代方程

令φi(x)=φ(x)/n，并将目标函数改写为：

分布式算法的核心思想是：每个节点根据本地和通信网络中相邻节点更新耗量微增率的估算值xi，直到所有节点的耗量微增率达到一致。根据梯度∇φi(xi(k))，xi(k)的迭代方程为：

式中：μij为通信网络中节点i和节点j之间的权重，由附录B 中metropolis 权重准则生成；σ为关于梯度的步长；k为迭代次数。

本 文 假 设x=[x1，x2，…，xn]T，h(x)=[∇φ1(x1)，∇φ2(x2)，…，∇φn(xn)]T，A=(μij)n×n，I为n×n阶单位矩阵，则式（10）的矩阵形式为：

考虑以下新的目标函数：

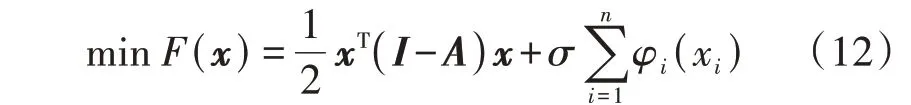
当x1=x2=…=xn时，（I-A）x=0，因此，xT（I-A）x是等耗量微增率在式（12）中的体现。当步长σ足够小时，新目标函数式（12）的优化结果接近于式（9）的优化结果［19］。式（12）的梯度gk为：

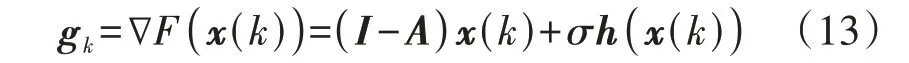
则海森矩阵Hk为：

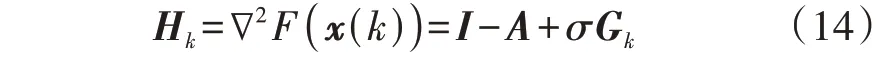
式中：Gk为对角矩阵，其对角元素(Gk)ii如式（15）所示。

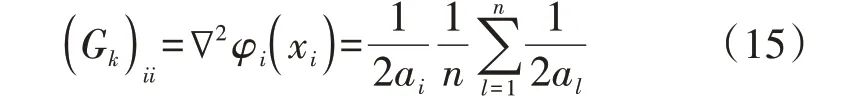
因此，关于二阶梯度的迭代方程为：

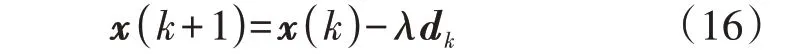
式中：dk为牛顿方向，dk=gk，为海森矩阵的逆矩阵；λ为关于dk的步长。

2.2 分布式拟牛顿法

牛顿法在求解的过程中通过海森矩阵引入二阶梯度信息，以牛顿方向为搜索方向进行更新，有更快的迭代收敛速度，但海森矩阵在稠密时的求逆计算量大，在海森矩阵无法保持正定时，其逆矩阵不存在，这会导致牛顿法失效。拟牛顿法则通过构建正定矩阵近似，克服了牛顿法的缺点。在附录C式（C1）—（C12）分布式拟牛顿法的推导过程中，gk第i个元素gi，k表达式中的功率偏移项zi(k)-zD-zloss需要全局信息，无法从本地获取，而在感性电网中，有功功率与频率强相关，无功功率与电压强相关，因此，功率偏移项可由本地频率／电压偏移间接得到。令RIC(Pi)=xPi，RIC(Qi)=xQi，根据附录C 式（C12），有功功率和无功功率的耗量微增率在第k次迭代时的梯度gi，k，P和gi，k，Q分别为：

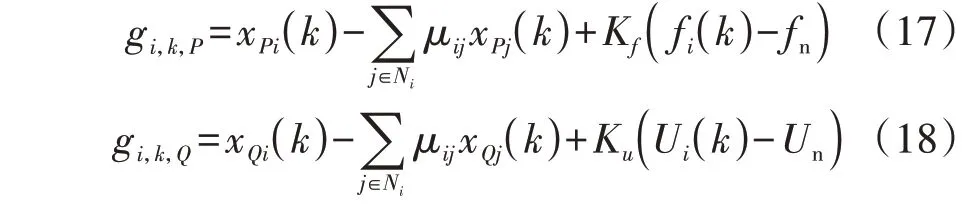
式中：Ni为与节点i相连节点的集合；Kf、Ku分别为频率和电压偏移系数；fi( )k为节点i处的频率在第k次迭代时的采样值；Ui( )k为节点i处的电压在第k次迭代时的采样值；fn为额定频率；Un为额定电压。

分布式拟牛顿法根据等耗量微增率准则优化功率分配的步骤如附录C图C1所示。

3 分布式经济运行控制策略

本文所提的分布式经济运行控制策略考虑了各DG的发电成本，能够实现高质量电压／频率控制和发电成本最优。图3 为混合VS-GSI 和CS-GSI 交流微电网的分布式经济运行控制策略框图，为了便于分析，假设节点i处的逆变器为VS-GSI，节点j处的逆变器为CS-GSI。图中：、分别为估算的节点i处有功、无功功率；Kp、Kq分别为有功、无功偏移系数；ΔQi为节点i处无功功率的估算值与实际值之差；Gi(s)为PI 控制器；δei为节点i处电压的微调量；δωi为节点i处频率的微调量；、分别为VS-GSI 外环d、q轴电压控制器的参考值；ug为输出电压；Nj为与节点j相连节点的集合；Φi=［Pi，Qi］为VS-GSI 在节点i的本地测量功率；Φj=［Pj，Qj］为CS-GSI 在节点j的本地测量功率为节点i处的参考频率；ωn为额定频率。每台逆变器的本地信息通过通信网络与相邻节点信息进行交换。无功功率控制器和有功功率控制器根据相邻节点和本地节点的信息Φk=［Pk，Qk］（k∈Ni∩Nj）计算得到耗量微增率，利用分布式拟牛顿法优化各台逆变器的输出功率，并实现电压和频率的控制。

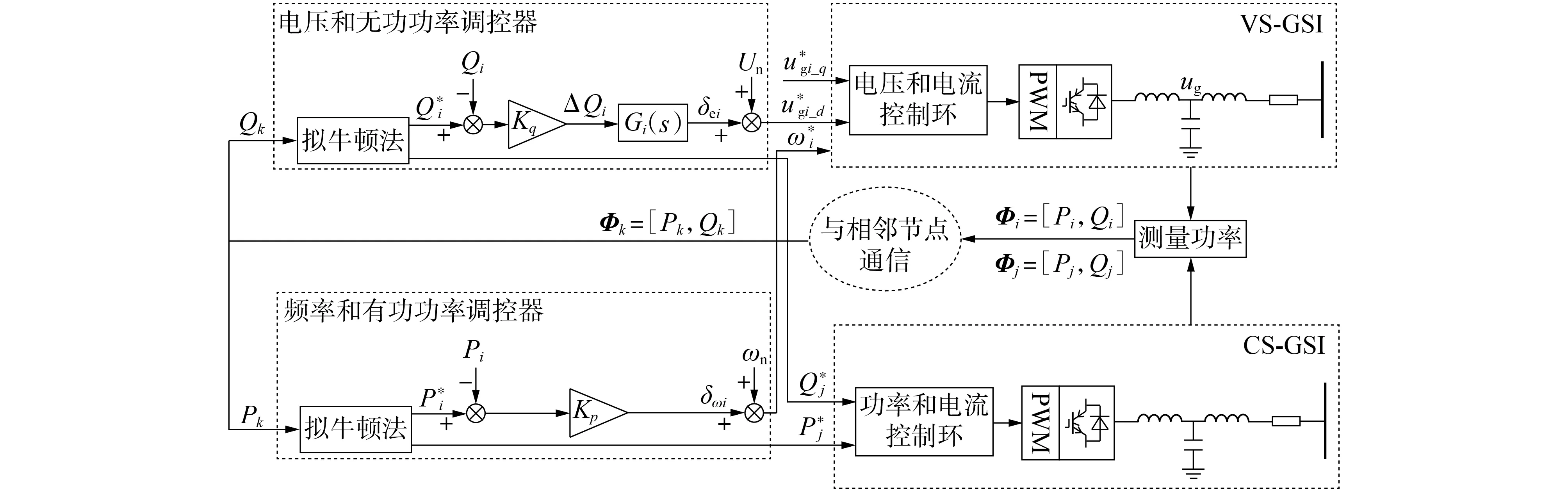
图3 混合VS-GSI和CS-GSI交流微电网的经济运行控制策略框图Fig.3 Block diagram of economic operation control strategy for AC microgrid with hybrid VS-GSI and CS-GSI

3.1 电压和无功功率控制

在微电网实际运行中，个别母线电压可以略微偏离额定值（通常小于5%）［20］，这为无功功率分配提供了至关重要的条件。在混合VS-GSI 和CS-GSI的微电网中，各节点通过通信网络与相邻节点交换无功功率测量值信息，进而，利用分布式拟牛顿法根据等耗量微增率准则优化无功功率分配，实现无功发电成本最小。

ΔQi经过PI 控制器Gi( )s后得到电压的微调量δei，进而控制VS-GSI实际输出的无功功率，因此，VSGSI外环d轴电压控制器的参考值为：

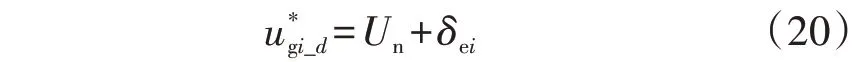
VS-GSI外环q轴电压控制器的参考值=0。

值得注意的是，式（19）将电压与无功功率相联系，无功功率的变化通过电压微调量δei影响电压的变化。此外，分布式拟牛顿法在无功功率的迭代过程中能够进一步减小电压偏移，如式（20）所示。

3.2 频率和有功功率控制

在混合VS-GSI和CS-GSI的微电网中，各节点通过通信网络与相邻节点交换有功功率测量值信息，进而，利用分布式拟牛顿法根据等耗量微增率准则优化有功功率分配，实现有功发电成本最小。

δωi与额定频率ωn相加后得到参考频率，为微电网提供频率支撑。

值得注意的是，式（21）将频率与有功功率相联系，有功功率的变化通过频率微调量δωi间接影响频率。此外，拟牛顿法在有功功率的迭代过程中能够进一步减小频率偏移，如式（22）所示。

4 算例分析

为了验证所提出的交流微电网经济运行控制策略的有效性，在仿真软件PLECS 中搭建如图2 所示的仿真模型。其中，6 台不同容量的DG 通过撑网逆变器（3台VS-GSI、3台CS-GSI）经具有不同阻抗的线路并联接入公共母线。主电路与控制回路的主要参数如附录D 所示。通信网络的结构为环形。交流微电网的初始负荷为1.38+j0.31 kV·A。

本文考虑2类成本函数［10，12］：

式 中：C1P，i(Pi)为 可 调 度DGi的 有 功 发 电 成 本，C2P，j(Pj)为不可调度DGj的有功发电成本，DG1—DG3的发电成本均为C1P，i( )Pi，DG4—DG6的发电成本均为C2P，j(Pj)。

4.1 负荷响应分析

本文所提控制策略基于分布式拟牛顿法以及改进的下垂控制实现功率的最优分配和电压／频率的高质量控制。为了显示本文所提策略的优越性，在相同的微电网中，将其与文献［2］中基于传统下垂控制的经济运行控制策略进行对比。文献［2］采用传统的电压-无功下垂控制将有功-频率下垂控制改进为有功等耗量-频率下垂控制，仅考虑有功功率的发电成本。在t=3 s 和t=6 s 时负荷均增加1.38+j0.31 kV·A，基于传统下垂控制的经济运行控制策略得到的电压和频率的仿真结果分别如图4（a）、（b）所示（图中频率与电压均为标幺值，后同），由于下垂控制固有的缺陷，电压和频率存在偏移，且随着负荷的增加而下降，在t=6 s 负荷较大时，电压跌落超过5%，较为严重。此外，基于传统下垂控制的经济运行控制策略采用电压-无功下垂控制，各DG 的无功功率耗量微增率不相等，如图4（c）所示，无功发电成本不能达到最优。

本文所提基于分布式拟牛顿法的经济运行控制策略的仿真结果如图5 所示。由图可以看出，频率基本运行在额定值，电压存在微小的偏移，在t=3 s和t=6 s负荷突增时，频率在较小的波动后快速稳定在额定值，而电压的偏移量随着负荷的增加而增加，但最大偏移量小于1.5%，仍然能够实现电压和频率的高质量控制，此外，本文所提经济运行控制策略能够使各DG 的无功功率耗量微增率相等，且随着系统负荷的增加，各DG 的无功功率耗量微增率也将动态调整并最终相等，使系统的无功功率运行成本最优。

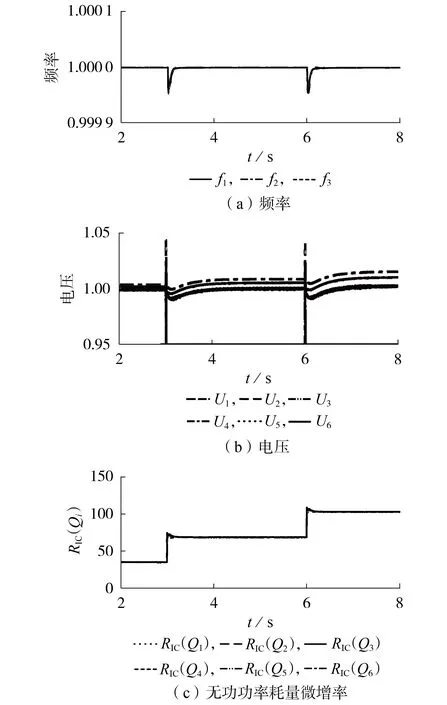
图5 所提经济运行控制策略的仿真结果Fig.5 Simulative results of proposed economic operation control strategy

相较于基于传统下垂控制的经济运行控制策略，本文所提经济运行控制策略能够实现高质量的电压和频率控制。此外，所提经济运行控制策略依据等耗量微增率准则实现有功功率和无功功率的最优分配，使系统发电成本最小。

4.2 逆变器故障

逆变器在发生故障退出运行时可能会影响系统的稳定性。本节研究所提经济运行控制策略对逆变器故障下系统的恢复能力，实现DG“即插即用”。

微电网的负荷始终保持为4.14+j0.93 kV·A。VS-GSI1在t=5 s 时发生故障退出运行，且通信网络发生相应变化。逆变器故障下系统的运行结果如图6 所示，在VS-GSI1发生故障后，其余GSI能够保持经济运行，各DG 的无功功率耗量微增率收敛且相等。当VS-GSI1在t=8 s 恢复运行后，6 台GSI 再次实现经济运行，因此，所提经济运行控制策略具有DG“即插即用”的能力，对逆变器故障有较强的鲁棒性。

图6 逆变器故障下系统的运行结果Fig.6 System operation results under inventer failure

4.3 通信故障

在系统运行过程中，通信系统也会出现故障，影响信息交换。本文对所提经济运行控制策略进行仿真测试来研究通信故障对系统稳定性的影响。

假设在t=2 s 时，节点1 和节点2 之间的通信链路因出现故障而断开，通信链路从环形的拓扑结构变为线形结构，在t=4 s时，节点1和节点2之间的通信恢复正常，且在t=3 s 和t=6 s 时负荷增加，系统仿真结果如图7所示。在通信故障发生后，各DG 的无功功率耗量微增率收敛且相等，系统依然能够维持稳定运行。与t=6 s通信正常时的动态效果相比，在t=3 s 通信链路故障且负荷发生突变时，各DG 的耗量微增率动态效果较差，但各耗量微增率依然能够实现收敛且相等。因此，所提经济运行控制策略对通信故障具有较强的鲁棒性。

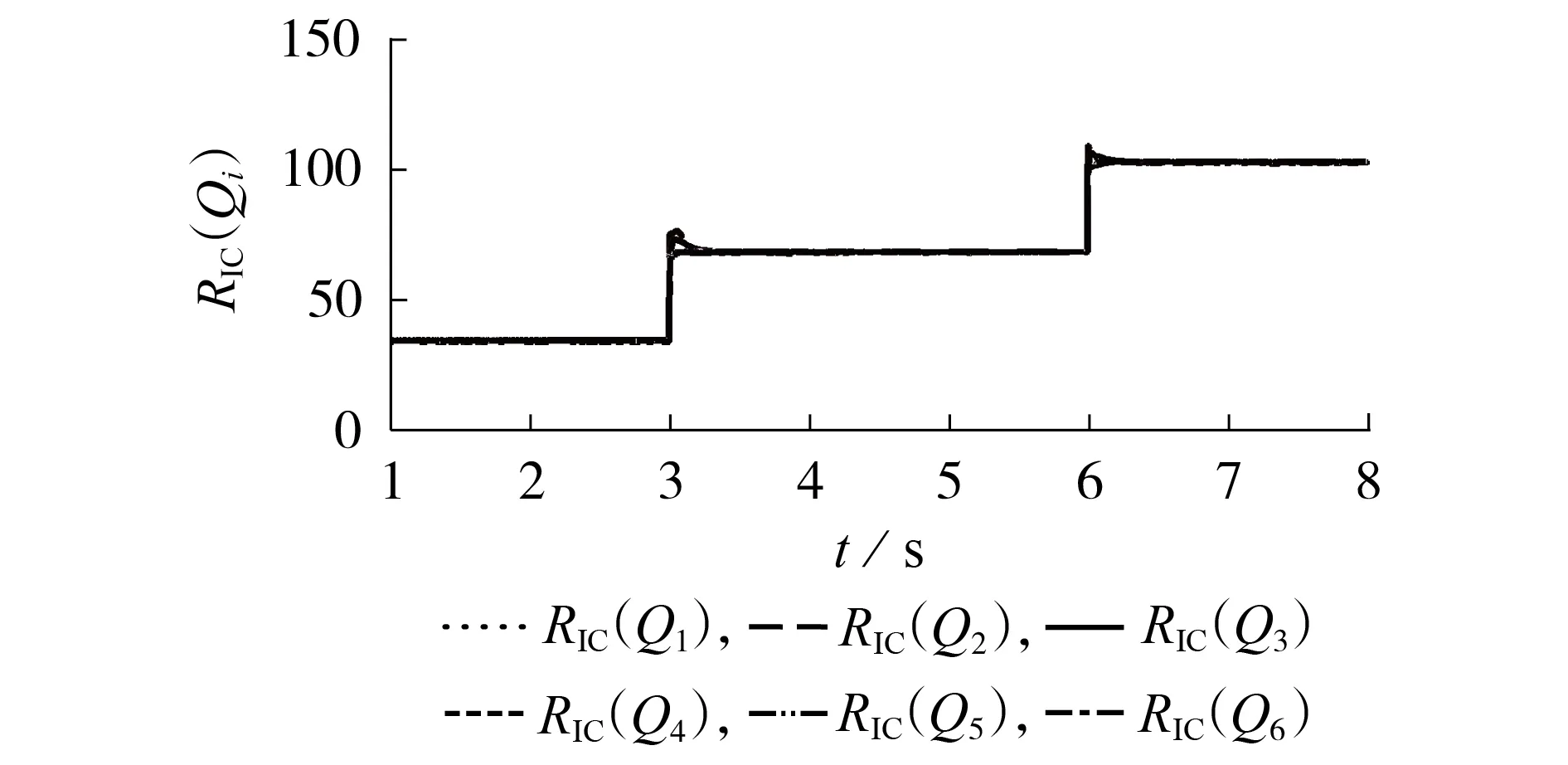
图7 通信链路故障下系统的运行结果Fig.7 System operation results under communication link failure

5 结论

本文针对混合VS-GSI 和CS-GSI 交流微电网提出一种基于分布式拟牛顿法的经济运行控制策略，并与基于传统下垂控制的经济运行控制策略进行仿真对比，所提经济运行控制策略的优点如下：

1）根据等耗量微增率准则并基于分布式拟牛顿法，所提经济运行控制策略能够实现有功发电成本和无功发电成本最小，并实现微电网经济运行；

2）所提经济运行控制策略基于改进下垂控制，使系统电压的偏移量小，且使频率运行在额定值，具有较强的电压和频率控制能力；

3）在面对线路阻抗不匹配、负荷变动、逆变器故障、通信故障等工况时，所提经济运行控制策略均具有较强的鲁棒性，能够实现电压以及频率的稳定控制。

附录见本刊网络版（http：//www.epae.cn）。