基于出行模式的注意力机制可解释性探索

翁小雄，田 丹，覃镇林，罗瑞发

1.华南理工大学 土木与交通学院，广州 510630

2.深圳市金溢科技股份有限公司，广东 深圳 518000

随着智慧城市进一步建设，其对个体出行预测任务提出了越来越高的要求。不仅要求保证个体出行预测的准确度，还应深入挖掘个体出行模式。出行模式可反映个体出行中相同或相似的出行记录。掌握个体出行模式有助于理解个体出行规律，帮助相关交通企业进行科学的运营管理，如为地铁线路规划工作提供可以信赖的决策依据。

近年来，深度学习模型，尤其是深度注意力模型大规模应用于个体出行预测任务[1]，在该任务的预测准确度上往往表现出优异的性能[2]。但通常深度学习模型具有黑箱性质，不能通过模型对个体出行模式提供有效解释[3]，导致人们对模型的信任度低。因此探索深度学习模型在个体出行预测任务中的可解释性是必要的。其中可解释性表示为人类可理解的出行模式对模型预测结果的重要性。

由于深度注意力模型中注意力机制的主要作用是为每一个输入分配权重[4]，其为探索模型的可解释性提供了切入点。在计算机领域的自然语言处理（NLP）任务中，Xie等[5]声称注意力机制反映了各输入对模型预测结果的重要性。Jain等[6]通过构造对抗注意力权重等实验提出注意力机制不能为模型预测提供有意义的解释。然而Wiegreffe等[7]反对了他们的观点，声称Jain等[6]做的实验不能完全否认注意力机制所发挥的作用。Vashishth等[8]探讨了注意力机制在什么条件下可以作为可解释性指标。结果表明，在单序列任务中注意力机制发挥的作用远不如多序列任务。在个体出行预测任务中，Li等[9]通过可视化少量样本的注意力权重，声称注意力机制可以识别模型不同重要程度的输入。现有关于模型可解释性的研究主要集中在NLP任务中，通过注意力权重擦除、置换等实验进行探索。其中擦除方法被广泛应用于消融实验[10]。在个体出行预测任务中，未考虑全样本下的可解释性，缺乏一个框架对出行预测进行系统地解释，并反映出行模式和模型所学习到的出行规律之间的关系。

地铁出行模式研究作为个体出行分析中重要一环[11]，本研究选取地铁出行及其出行模式作为研究背景。为了全面探索深度注意力模型在个体地铁出行预测任务是否具备可解释性，即注意力机制是否能通过学习出行模式来把握出行规律，本文提出基于出行模式的注意力权重擦除方法和可解释性评估框架。并结合个体出行模式规律，开发了3种不同的应用场景，验证模型的可解释性。

1 问题定义

1.1 个体地铁出行预测的问题定义

研究基于出行模式的注意力机制可解释性强，首先引入两个基本概念以定义个体地铁出行预测任务。

定义1（出行记录）通过一个四维元组来描述：

式中，R表示一次出行的刷卡记录，o、d、w、t分别表示出发站、目的站、工作日/非工作日（0表示工作日，1表示非工作日）和入站时间（h）。

定义2（出行序列）

给定历史出行序列Sm=(R1,R2,…,Rm)，个体出行预测任务可以定义为通过历史出行求解函数f，该函数实现通过历史出行序列映射下一次出行记录的站点，其数学定义如下：

式中，l表示模型预测的结果，预测的站点类型可以是o或d。

1.2 个体地铁出行模式

出行序列中具有完全相同的出行记录R，即o、d、w、t四个属性均相同，则定义为同一种个体出行序列的出行模式，记为P。假设个体u在给定的出行序列Smu下，相应的出行模式集合表示为：

式中，nu表示出行序列Smu下具有出行模式的数量。假设其中一种出行模式Pi具有出行记录Ri1,Ri2,…,Rin，则满足Ri1=Ri2=…=Riniu。

2 地铁出行的深度注意力预测框架

个体出行预测框架如图1所示，输入一个出行记录序列，经过嵌入层对每个出行记录的离散的4维属性o、d、w、t进行特征的降维映射。时间序列处理层对每个出行记录的嵌入向量按时间先后顺序进行处理。注意力层即对时间序列处理层输出的中间表示分配不同的注意力权重，这些中间表示与每个出行记录一一对应。最后使用全连接层和softmax层对注意力层输出的结果进行推断，得到最终的预测结果。

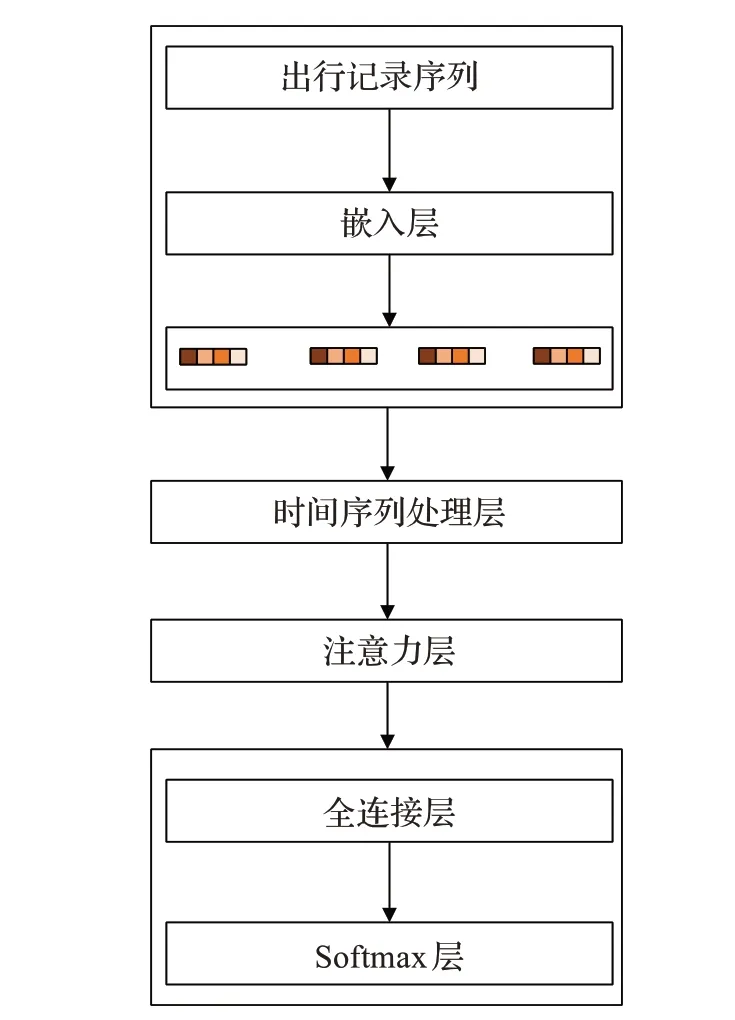
图1 地铁出行的深度注意力预测框架图Fig.1 Overview of deep attentive model for individual metro mobility prediction

2.1 嵌入层

嵌入层主要采用被大规模运用于自然语言处理领域的词嵌入方法[12]，该方法可以将离散属性转化为低维的参数向量，这些向量的参数可以通过神经网络的反向传播进行学习。地铁的个体出行属性中o、d记录了一次出行的空间位置，w表示了工作日出行和非工作日出行两种状态。将入站时间t作为一种离散属性输入，是因为出行模式更倾向于反映在每小时离散的时间点，而不是连续的数值。因此，通过词嵌入对这四个属性进行嵌入处理，更容易使模型生成与出行属性相关的特征。该运算表示为：

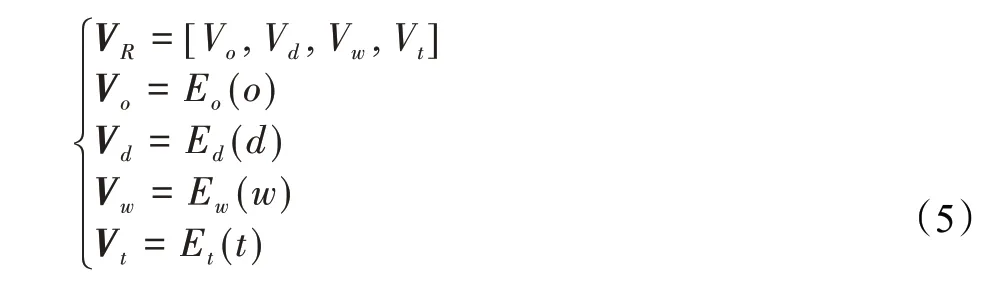
式中，E表示词嵌入运算，V表示嵌入向量。

2.2 时间序列处理层

使用时间序列层对出行模式的周期规律进行学习。出行序列经过嵌入层处理得到的嵌入向量序列[VR1,VR2,…,VRm]作为该模块的输入，然后输出隐藏向量序列[h1,h2,…,hm]。其中，[h1,h2,…,hm-1]称为候选向量，hm称为查询向量，作为注意力层的输入。该层通常可以使用深度循环神经网络来实现，如图2所示，其中时序单元可以是RNN、LSTM或GRU等循环网络单元。

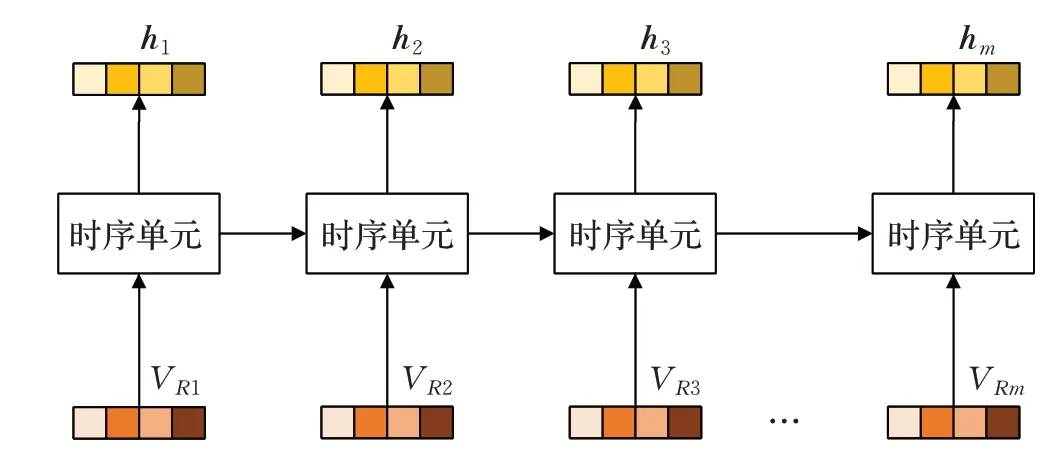
图2 时间序列层Fig.2 Temporal sequence layer

2.3 注意力层

注意力层[13]的作用是计算查询向量与候选向量之间的相似度，即通过最近一次出行与历史出行进行比对，为模型提供全局的历史信息，从而实现更高的预测精度。该模块通常使用一层全连接网络和softmax层组成，如图3所示。计算公式如下：

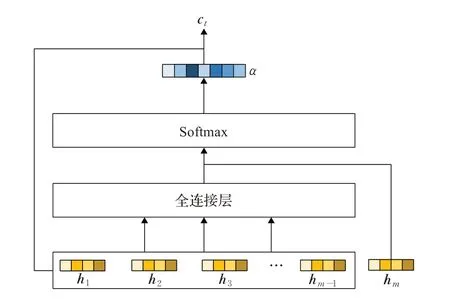
图3 注意力层Fig.3 Attention layer

式中，向量u1,u2,…,um-1由全连接网络生成，αi代表注意力权重，由ui经过softmax函数运算得到。上下文向量ct表示历史出行与当前出行的相关加权信息。

2.4 全连接层和softmax层

最后一个模块由全连接层和softmax层组成，输入ct，输出出行站点预测分布p，然后通过argmax函数得到模型决策结果l，其计算公式为：

式中，其中fc表示全连接层的运算，预测分布p表示了所有的地铁站作为下一次预测站点的概率值，而argmax函数则选择最大概率值对应的位置作为模型决策结果l。

3 基于出行模式的注意力可解释性评估框架

3.1 基于注意力权重的出行模式

在个体出行预测任务建模中，深度注意力模型可以为历史出行序列输入的每一个记录分配注意力权重。在给定出行序列Smu下，出行模式Pi下所有出行记录的注意力权重为αi1,αi2,…,αiniu，则定义Pi的注意力权重为Wi=(αi1,αi2,…,αiniu），其大小为该模式下所有出行记录的权重之和Ai=

为了探索个体u的出行记录所对应的出行模式对模型预测的影响，通过对各个出行模式的注意力权重大小A11,A12,…,A1nu进行降序排序得到相应的出行模式的排序：Bu={P'1,P'2,…,P'nu}。

当注意力模型能够通过分配注意力权重的过程挖掘对预测起关键作用的出行模式时，则出行模式按注意力权重的降序排序将提供最有用信息，即出行模式的权重大小和这个出行模式对模型预测的重要性是高度相关的。

3.2 基于出行模式的注意力权重擦除方法

为了探索各个出行模式对模型预测的不同影响，提出基于出行模式的注意力权重擦除方法。该方法通过擦除出行模式相应的所有出行记录的注意力权重。然后对所有注意力权重重新归一化，以保证不会出现训练期间从未遇到的情况，即出行记录的编码表示hi被人为地变为0。计算公式如下：

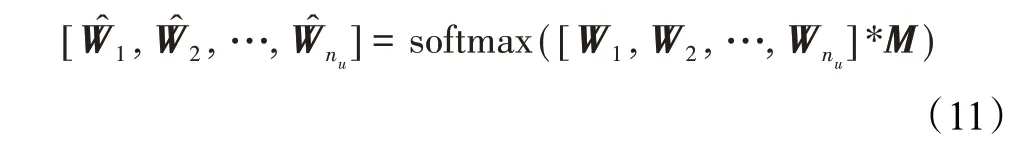
其长度等于注意力权重组的数量。出行模式被擦除时，其所对应的在M中用0表示。该方法的过程如图4所示。

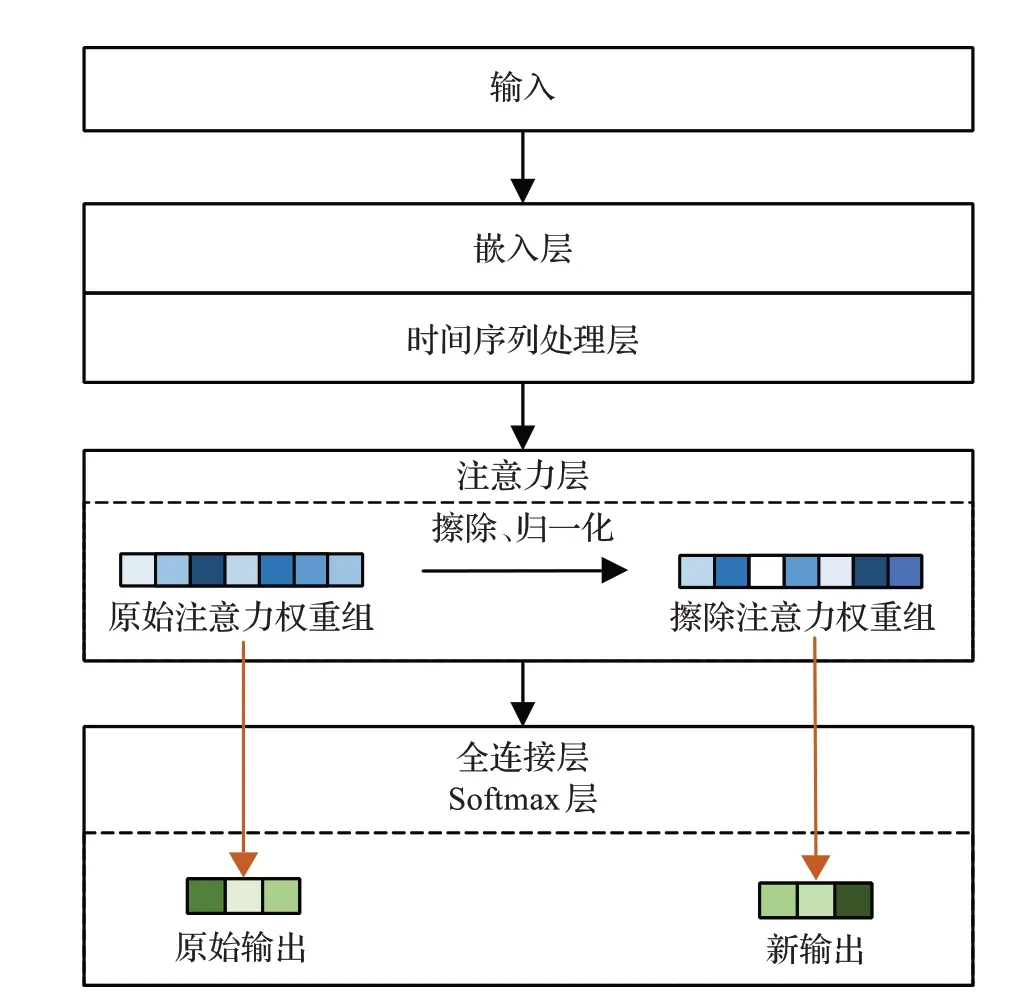
图4 注意力权重擦除方法流程图Fig.4 Attention weight erasure method

3.3 注意力权重擦除效果评估

为了衡量模型注意力权重组擦除前后决策结果的变化，引入JS散度（Jensen-Shannon divergence）和决策翻转（decision flip）作为评价标准[11]。

首先，JS散度[14]用来衡量擦除前后模型预测分布的变化：

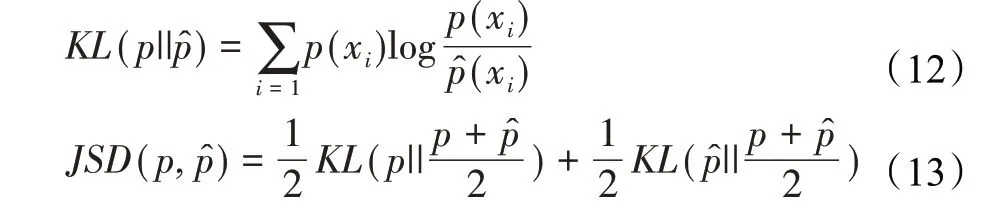
其次，决策翻转表示擦除操作前后模型决策结果发生变化，即

式中，l和l分别表示基于出行模式的注意力权重擦除前后的模型决策结果。根据决策翻转定义，计算擦除实验中的决策翻转的样本比例：

式中，rs表示发生决策翻转的样本数量，Ns表示样本总数量。其次，提出使得模型发生决策翻转的出行模式被擦除的比例的计算如下：

式中，rp表示一个样本被擦除的出行模式p的数量，Np为该样本出行模式的总数。

4 实例分析

4.1 数据处理

使用广州地铁羊城通刷卡数据进行实例分析。该数据的时间跨度为2017年2月1日至2017年5月31日，包括9条地铁线和157个地铁站。随机选择该时间段内出行不少于60次的乘客卡号。根据出行记录的定义和公式（1），通过所选乘客相应的刷卡记录构造数据集。

根据出行序列的定义，假设滑动窗口长度m，在给定的时间跨度下，对单个乘客的长度为M的出行序列进行采样，则第i个出行序列样本可以表示如下：

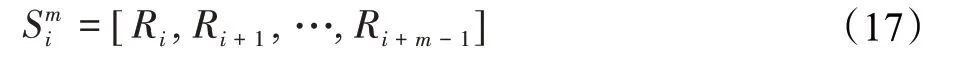
式中，1≤i≤M-m+1。

由于不同个体在一定时间周期内出行次数不一，为了对比研究不同长度出行序列预测任务下的出行模式的注意力机制可解释性，且本文所定义模型需要输入长度一致的数据，因此需将数据按照序列长度要求进行划分。序列长度的选择应可能多地包含个体在相应的时间周期内的出行次数，有利于模型能通过这些序列学习到相应周期的出行模式。结合个体出行规律，以周、半月、月作为三个周期维度，统计每个个体出行次数。如图5所示，发现周、半月、月出行次数分别为20、40、80次可以包括95%的出行人群在相应周期下的出行次数，因此m取值为20、40和80。通过公式（17）得到出行序列样本，再按照8∶2的比例划分为训练集和测试集。

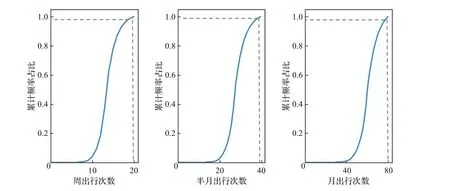
图5 出行次数累计频率曲线图Fig.5 Graph of cumulative frequency of trips

4.2 模型预训练和性能评估

在实例分析中，将地铁出行预测任务定义为目的站预测，即预测第m+1次出行的目的站。在该任务中，将第m+1次出行的o、w、t输入嵌入层，并通过时间序列处理层转化成一个查询向量，并和由前m次出行记录得到的候选向量一起输入注意力层。时间序列处理层选用了门控循环网络（gated recurrent unit，GRU）[15]。在模型训练阶段，选用交叉熵函数作为损失函数[16]并以准确率作为评估模型性能的指标：

式中，T表示模型预测准确的样本数量，N表示模型预测错误的样本数量。如表1所示，随着序列长度增加，模型训练后性能提升，预测精度可达70%以上。

表1 模型性能评估Table 1 Model performance evaluation

4.3 单一出行模式的注意力权重擦除实验

为了衡量最大注意力权重的出行模式对模型预测的影响，使用单一出行模式的注意力权重擦除方法对出行模式注意力权重进行擦除。为了对比最大注意力权重的出行模式擦除实验结果，设置了随机注意力权重的出行模式擦除实验作为对照。最大注意力权重的出行模式和随机注意力权重的出行模式分别记为P*和Pr。

首先，采用下式量化两种擦除实验对模型的预测分布影响程度的差值：

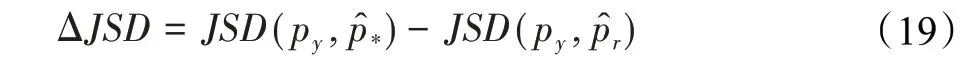
式中，py表示原模型的预测分布，p*和pr分别擦除P*和Pr的注意力权重后模型的预测分布。然后，计算P*的注意力权重值与Pr的注意力权重值之间的差值：

图6展现了所有样本的ΔA-ΔJS的散点图，横轴表示样本的ΔA，纵轴表示样本的ΔJS。从图6可以看出长度序列为20、40和80的出行序列在该实验中表现相近。此外，大部分样本的ΔJS>0，表示擦除出行模式P*比擦除出行模式Pr对模型预测分布影响更大。从蓝色的二次拟合曲线看，存在ΔJS随ΔA增大而增大的趋势。在ΔA=0.4附近，样本散点的ΔJS走势陡峭向上，意味着P*与Pr的注意力权重差值在0.4水平以上时能更显著反映出两种出行模式擦除对原模型预测分布的影响。在ΔA=0.2附近，可以观察到0.2以内有极少量的样本散点表现出ΔJS<0，表示出行模式Pr比出行模式P*对模型预测分布影响更大。然而这种情况发生在两种模式的权重比较接近时，而且只在少量样本中发生。从对模型预测分布的影响的层面看，具备最大注意力权重的出行模式P*对模型结果影响更大。

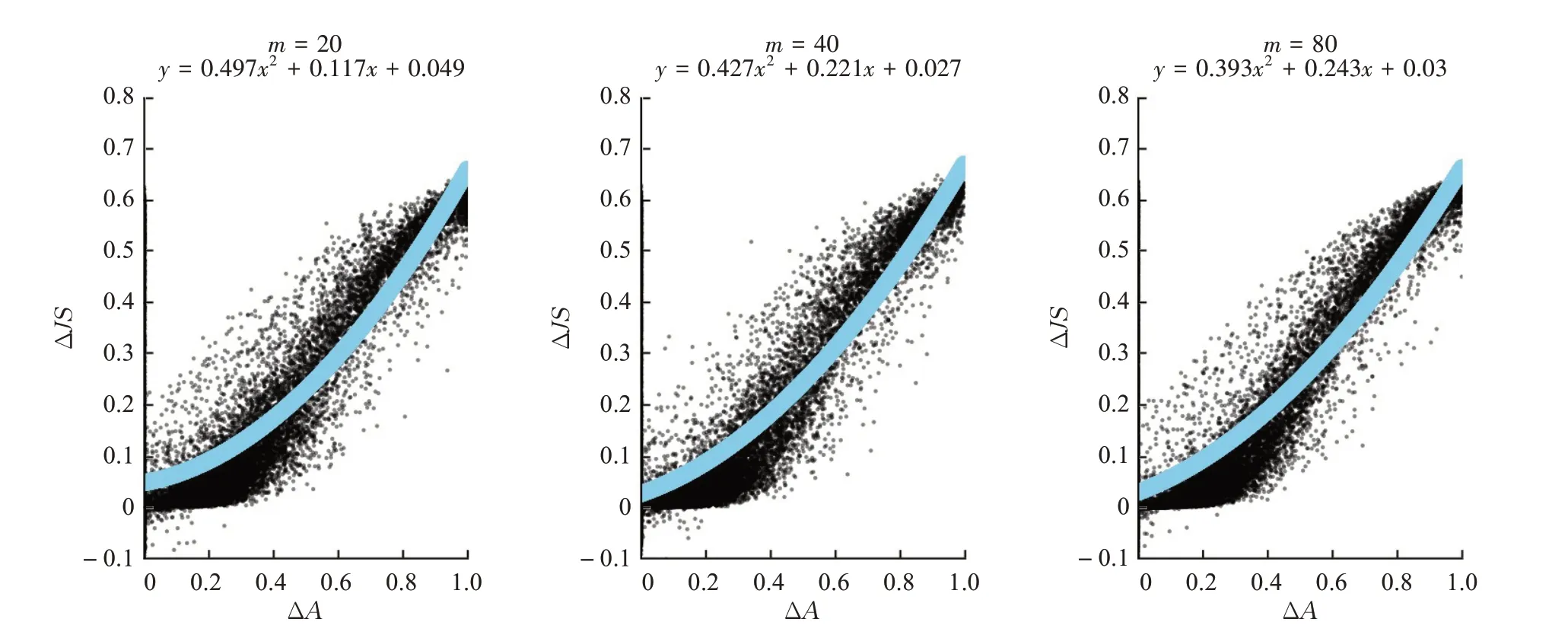
图6 ΔA-ΔJS的散点图Fig.6 Scatter diagram ofΔA-ΔJS

为了从一个更为直观的角度衡量擦除两种出行模式对模型预测结果的影响，利用决策翻转指标对P*和Pr擦除影响进行进一步分析。

从表2可以看出，在三种不同长度的出行序列中，擦除P*翻转而擦除Pr不翻转的比例显著高于擦除Pr翻转而擦除P*不翻转的比例，可以认为擦除P*比擦除Pr更显著引起模型发生决策翻转。且随着序列长度增加，擦除P*和擦除Pr同时翻转的比例下降，说明序列长度越长，单一模式的擦除对模型决策影响下降。因为序列长度增加，模型可学习更多的个体出行特性，此时仅对单一出行模式擦除，无法完整获知其模式反映的个体出行信息，模型的解释难度增加。然而三种序列长度下，大部分样本（70%以上）在擦除P*和擦除Pr都不发生决策翻转，代表擦除单一出行模式的注意力权重在决策翻转的指标下，还不足以充分反映最大注意力权重的出行模式和模型预测结果的高度相关性。

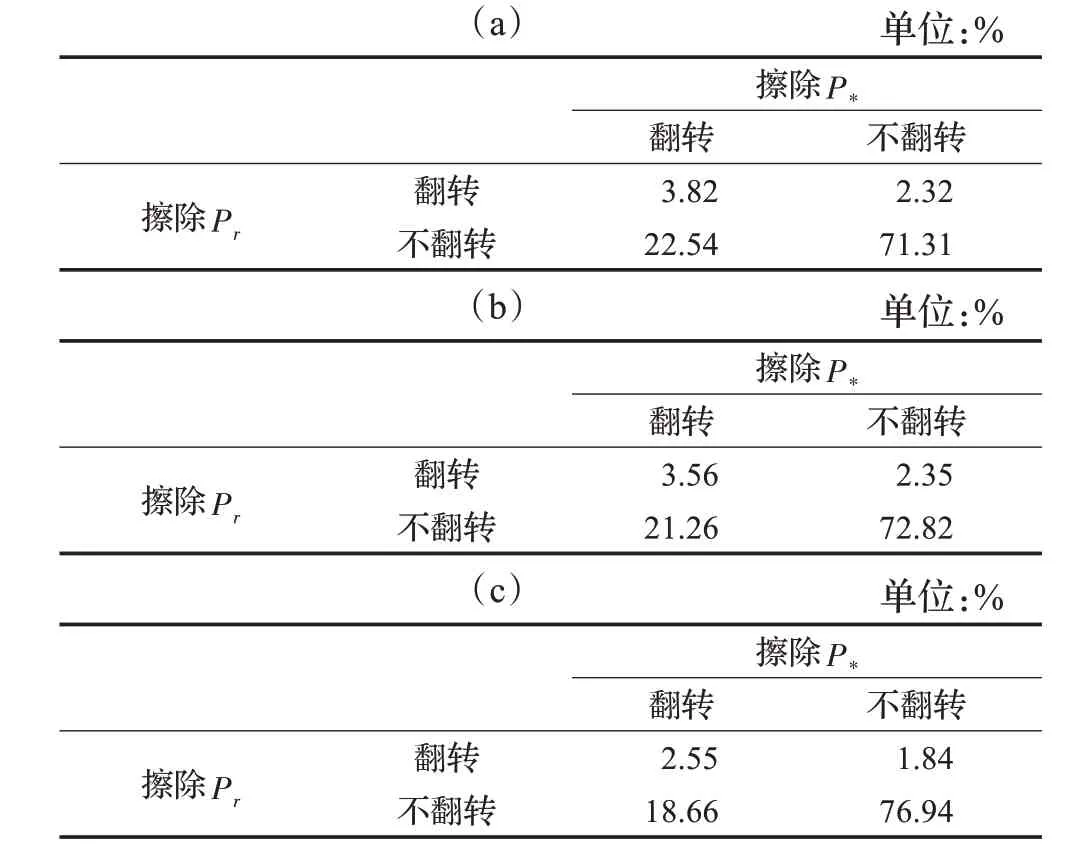
表2 三种出行序列长度的决策翻转样本的比例Table 2 Percent of decision flip samples with 3 sequence lengths

4.4 一组出行模式的注意力权重擦除实验

为了进一步探索同时擦除多个出行模式的注意力权重对模型预测的可解释性影响程度，对一组出行模式的注意力权重进行擦除来评估出行模式组合对模型预测结果的影响。本实验中，出行模式按照一定排序方式依次对其相应的所有出行记录的注意力权重进行擦除，直到模型预测结果发生决策翻转。然后计算每一个样本在该排序下需擦除多少比例的出行模式引起决策翻转(Rp)。

为了验证3.1节的按注意力权重降序排列的出行模式是否会为模型提供一个最简洁的解释：即具有较大的注意力权重的出行模式对模型预测影响也较大，因此擦除这些出行模式的注意力权重可能会使模型预测更容易出现决策翻转。为此设计了三种出行模式的排序方案作为3.1节的降序排序的对照实验。这四种排序方案如下：

（1）出行模式的注意力权重大小的降序排序，即3.1节的排序顺序。

（2）出行模式的注意力权重大小的随机排序。

（3）出行模式的注意力权重的梯度的降序排序。

（4）出行模式的注意力权重的梯度的升序排序。

图7表示序列长度20、40和80的出行序列的样本的Rp分布箱图，左右按顺序分别表示四种排序方案。纵向对比发现，序列长度增加，Rp的中位数减小，分布下移。说明给定的序列长度越长，其中所包含的每一个出行模式会具有更多关于出行规律的信息。因此对越长序列的出行模式进行擦除，控制同一种注意力排序方式，擦除出行模式直至决策翻转的速度更快，所需的擦除比例更小。

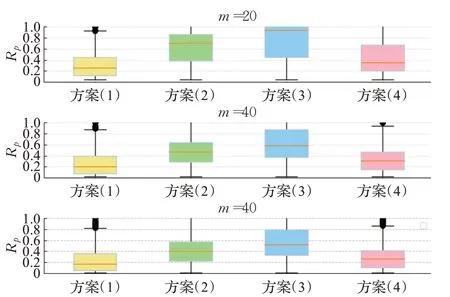
图7 Rp分布箱图Fig.7 Boxplot of Rp distribution

横向对比发现，方案（1）在四种方案中最快使得模型预测发生决策翻转，有一半的样本在Rp=0.2附近发生了决策翻转。表现次优的是方案（4），有一半的样本在Rp=0.3附近发生了决策翻转。表现最差的是方案（3），其效果不如随机排序的方案（2）。由于注意力权重的梯度表示了注意力层的权重对决策函数的变化率，梯度越小意味着注意力权重对模型决策影响更稳定。从梯度升序的方向对出行模式的注意力权重进行擦除能取得和方案（1）的排序接近的效果，意味着较大的注意力权重所对应的出行模式同时对应着较小的注意力梯度。而当梯度以降序排序时其效果反而差于随机排序，从另一个角度说明由于较大的注意力梯度所对应的出行模式同时对应着较小的注意力权重，从较小的权重开始擦除会导致模型发生决策翻转的效率下降。因此，模型学习出行模式的规律时，会对权重较大的出行模式分配稳定的注意力权重。因此，在一组出行模式的注意力权重擦除实验中，深度注意力模型不但可以为重要的出行模式分配较大的注意力权重，且该分配过程具有较高的稳定性。

5 结论

本研究以个体地铁出行预测为任务背景，探索注意力模型基于出行模式的可解释性。本文根据地铁出行预测任务定义了个体的出行模式，并以目的地预测作为实例分析任务，通过广州地铁羊城通数据训练了准确率高达70%的地铁出行预测注意力模型。然后通过单一出行模式的注意力权重擦除实验和一组出行模式的注意力权重擦除实验，可以得出以下结论：

（1）衡量单一出行模式对模型预测分布和决策结果的影响，发现最大注意力权重的出行模式对模型预测影响大于随机注意力权重的出行模式，但在两种擦除方法下大多数样本预测结果均未受到影响，即这种影响是有限的。且随着序列长度增加，单一模式的擦除对模型决策影响下降，即该条件下注意力机制更不容易为模型提供可解释性信息。

（2）衡量一组出行模式对模型预测结果的影响，发现按注意力权重降序排列擦除出行模式，表现出使模型发生决策翻转最优的效果。说明深度注意力模型通过对各个出行记录分配注意力权重来区分不同重要程度的出行模式，并且越重要的出行模式所分配的注意力权重越稳定。因此，可以通过权重的降序排列方法找到对模型决策重要度高的出行模式集合。且随着序列长度增加，需擦除的出行模式占比降低，即此时注意力机制更容易为模型提供可解释性信息。