改进ARA*算法的移动机器人路径规划

黄梦涛，李智伟

西安科技大学 电气与控制工程学院，西安 710600

路径规划是实现移动机器人自动导航的一个关键环节。路径规划是按照给定的地图和目标位置，规划出一条使机器人抵达目标位置的路径，它通过统筹全局信息，制定高效、安全的移动策略[1]。

路径规划可以按照规划范围划分为全局、局部路径规划，环境信息完全已知时，才能实现全局路径规划[2]。全局路径规划算法可以分为传统方法和仿生智能方法，传统方法中最典型的有A*算法、快速扩展随机树（rapidexploration random tree，RRT）算法等；仿生智能方法有遗传算法（genetic algorithm，GA）、蚁群算法（ant colony algorithm，ACA）、粒子群算法（particle swarm algorithm，PSO）等[3]。

传统方法中，A*算法因为能在较短时间里有效地求解出最短路径，被广泛应用于各个领域，然而，A*算法的启发式函数构造简单，算法在执行过程中会出现较多冗余节点，耗费时间较长[4-5]。RRT算法普适性强，不仅可以工作在二维地图，也适用于高维空间，因此更多地应用于机械臂的路径规划，但是RRT算法得到的路径质量不高，折转次数多，解的最优性较差，工程应用时往往使用的是与势场法结合后的改进RRT算法。

仿生智能方法中，遗传算法从多个初始点开始操作，而不是从某一个单独点开始，很大程度上避免了搜索过程中过早收敛于局部极值，因此更有可能求得全局极值，但同时也使得计算速度较慢全局路径搜索的效率相对较低，算法迭代进化时会产生一些没有意义的种群，不适合实时路径规划。蚁群算法采用正反馈机制，使搜索过程不断收敛，而且蚁群算法具有分布式计算能力，可以在全局多点同时搜索最优路径，因此计算效率较高，但是由于蚁群算法初期信息素的缺乏，容易陷入局部最优，虽然蚁群算法初期收敛速度快，但在后续容易发生路径迂回和死锁[6]。粒子群算法的收敛速度快，需要设置的参数较少，简单易行，但也容易陷入局部最优。

1 文献综述

针对上述几种路径规划算法的缺陷，当前有众多科研工作者提出了改进方法。文献[7]提出了一种改进的A*算法，通过引入环境障碍物比率K，量化了环境中的障碍物信息，根据K值调节启发函数的权重，提高了算法效率和灵活性，另外，基于Floyd算法思想设计了一种路径节点优化算法，剔除了冗余节点，提高了路径平滑度，但是随着启发函数的权重变化，路径的最优性会受到影响，K值越大，搜索速度越快，路径的最优性就越差，所以应该加入约束条件来限制K值的增长；文献[8]针对传统RRT算法内存消耗大的问题提出了一种基于简化地图的区域采样RRT*（simplified map-based regional sampling RRT*，SMRS-RRT*）算法，首先简化栅格地图，再用PRM算法寻找最优路径作为引导路径，通过智能采样因子扩大引导路径得到智能采样区域，在其中迭代搜索找到一条代价小且无碰撞的路径，最后结合最小转弯半径约束和B样条曲线优化路径，但是这种简化地图的方法比较简单，仅通过障碍物占用的栅格数量与设定的阈值比较，剔除占用栅格少的一部分障碍物，因此无法保证最终生成路径的安全性；文献[9]针对遗传算法在初始化种群时计算方法的不足，提出利用SPS（surrounding point set）算法在障碍物周围生成点来产生初始路径，提高算法快速生成初始种群的能力，增加平滑、删除算子，删除不必要的路径节点，使路径更平滑，最后结合小生境法保持种群多样性，避免出现早熟现象，但是删除算子只能作用于路径节点初次与障碍物连接的地方，每处障碍物至多删除一个多余节点，因此对路径的收敛速度和平滑性提升不大；文献[10]提出了一种改进的蚁群算法，将蚂蚁搜索方向扩展为16方向24邻域，结合向量夹角的思想设计出新的启发信息计算方法，引入转移概率控制参数δ调控算法搜索范围，提高了路径寻优效果和搜索效率，虽然文中说明了δ=0时算法类似于贪心算法，δ=1时算法采用轮盘赌策略，但是没有说明δ的具体取值方法，而且蚁群算法容易陷入局部最优的问题没有解决；文献[11]提出了一种任意时刻启发式搜索ARA*算法，它首先在一个较短时间内找到一条非最优可行路径，然后在接下来的时间中尽可能地优化，如果时间足够多的话，可以找到一条最优的可行路径，ARA*算法会重复使用之前的搜索结果，这使得它比其他的任意时间规划算法更加高效，但是算法效率提升不明显[11]。

现阶段针对路径规划算法的改进集中于执行效率和路径的平滑程度这两方面，也就是说，在路径规划算法应用于实际工程之前，需要着力于提升算法的实时性和安全性。因此，本文在ARA*算法的基础上做出了改良，使路径规划的效率提升更显著，另外还提出了一种自适应选择节点间连接方式的策略，兼顾了4连接和8连接的优点，降低了安全风险的同时，缩短了路径长度。

2 ARA*路径规划算法介绍及分析

ARA*（anytime repairing A*）算法是A*算法的一种改进算法：是在WA*（weighted A*）算法[12]基础上做了进一步改动，着重于解决实际的工程问题，优先考虑算法的执行速度，并且算法的可移植性也得到了明显的改善，本章对ARA*算法做简要介绍。

ARA*算法在代价估计函数f(s)中加入膨胀因子ε。

其中，s表示当前节点，g(s)是从起点到当前节点的实际代价，h(s)是从当前节点到终点的代价估计值，f(s)则是从起点到终点的代价。算法运行时，膨胀因子ε从设定初值开始逐渐减小，在时间允许的范围内εmin=1，如果时间不够充足ε会尽可能地接近1，那么最后只能求得路径的次优解，也就是说路径的次优性由ε决定，且路径的长度不大于最优路径的ε倍[13]。

图1是A*算法得到的路径，图2是在同样的栅格地图中ε值不同时ARA*算法规划出的路径。通过对比图1和图2（c）得出结论，ε=1时路径长度最短，而且此时ARA*算法等价于A*算法，路径是最优的。

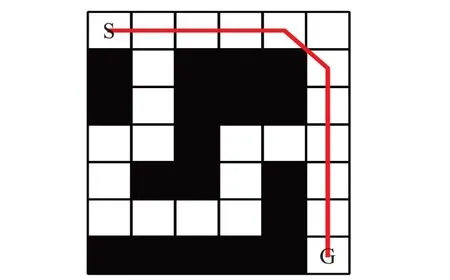
图1 A*算法得到的路径Fig.1 Path obtained by A*algorithm

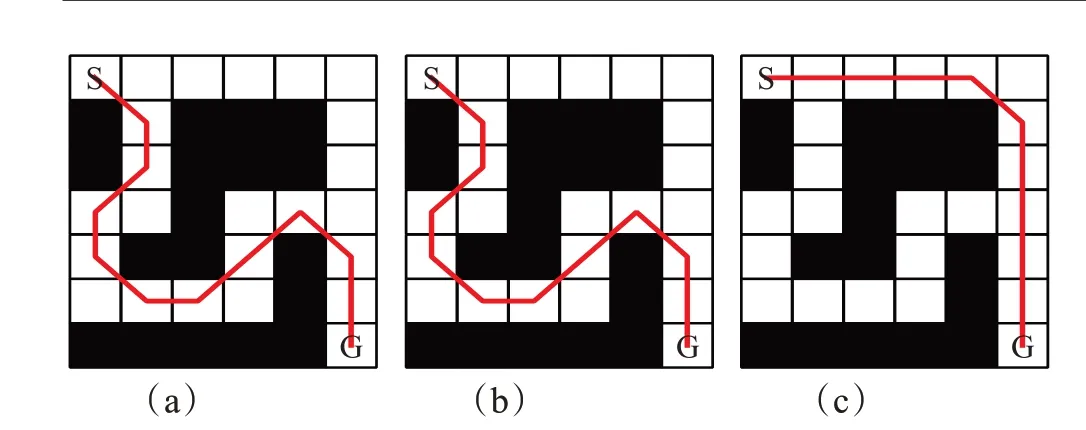
图2 ε值不同时ARA*算法得到的路径Fig.2 Path obtained by ARA*algorithm with different ε

ARA*算法用三种列表存放不同状态的节点：

（1）OPEN列表：存储具有局部不一致状态的节点。

（2）CLOSED列表：存储已经扩展过的节点。

（3）INCONS列表：当存储在CLOSED列表的节点g(s)值又降低时放入该列表中。

ARA*算法的局部不一致状态[14]：如果一个节点的g(s)值在它下一次被扩展之前降低，就认为该节点处于局部不一致状态，针对任意节点s'，假设节点s是它的最优前继节点，则它们应满足公式（2）：

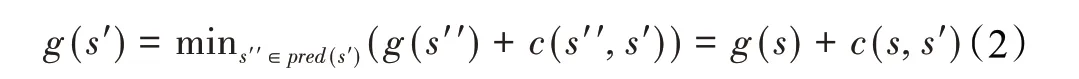
公式（2）中c(s,s')是从节点s到s'的代价，假如等式右侧值减小，如公式（3）所示：

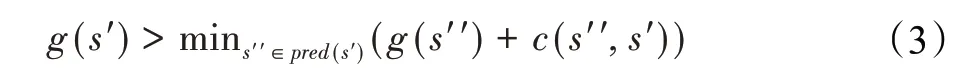
g(s)值的降低意味着节点s的g(s)值和其后继若干节点s'的g(s')值之间并不满足公式（2）的等价关系，这就是当前节点与它的前继节点之间存在的局部不一致。

在已经构建好栅格地图中，ARA*算法会从起点Sstart开始扩展，把与Sstart相邻的8个子节点加入OPEN列表，再根据公式（1）规定的启发式搜索规则从OPEN列表里搜索f(s)最小的节点作为下一个被扩展的节点，然后对下一个被扩展的节点执行同样的步骤，以此类推。随着路径的推进，有些节点的g(s)会降低，如果该节点已经存储在OPEN列表里，而且它是当前被扩展节点的子节点，则需要对它的g(s)重新计算。ARA*算法的执行流程如图3所示。

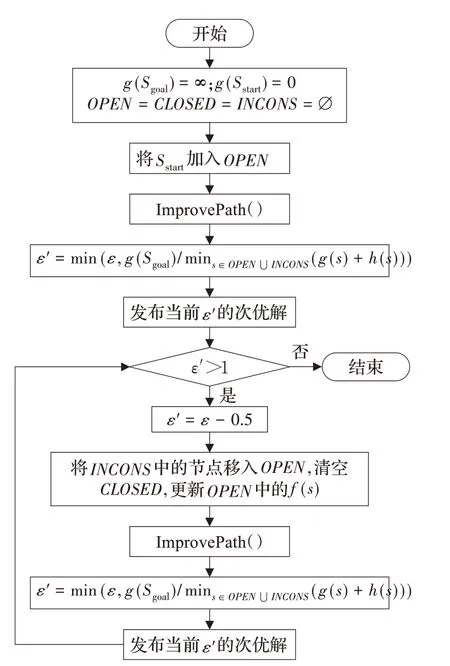
图3 ARA*主流程Fig.3 Mainstream of ARA*algorithm

图4表示主流程中节点的更新过程。首先，从OPEN列表中检索f(s)值最小的节点s，把s从OPEN列表中移除，再将它存储到CLOSED列表中，表示s已经被扩展过，如果s的子节点s'中某些节点的g(s')值比扩展前更低，当这些节点s'不在CLOSED列表里，则将它们存储到OPEN列表；否则，将它们存储到INCONS列表。

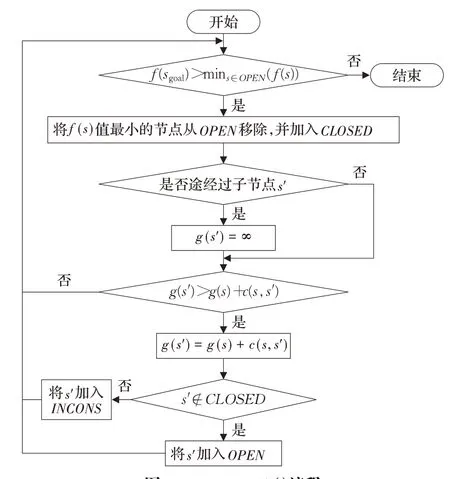
图4 ImprovePath（）流程Fig.4 ImporvePath（）process

在ARA*算法的运行过程中，随着路径从起点到终点的推进，会不断地在OPEN列表中搜索f(s)值最小的节点作为下一个被扩展的节点，每向前推进一个节点，就要从当前被扩展节点的周围至多8个子节点中搜索f(s)最小值，因此，加快搜索f(s)最小值的速度，ARA*路径规划的效率就会提高。

3 改进的ARA*路径规划算法

本文在ARA*算法中引入二叉排序树存储代价估计函数f(s)的计算结果，提高ARA*算法的执行效率；通过制定自适应节点选择策略，降低机器人与障碍物碰撞风险。

3.1 在ARA*算法中引入二叉排序树

传统ARA*算法的OPEN列表采用的是顺序存储结构，如图5所示。顺序存储结构的优点是：逻辑上紧邻的存储单元在物理位置上也是紧邻的，可以节省内存空间，并且可以实现随机存取[15]。但是，顺序存储结构的插入或删除运算不方便，除了结尾位置，在其余任何位置上实现插入或删除都不得不移动大量的数据元素，效率较低。为了加快在OPEN列表中搜索f(s)最小值的速度，需要找到一种数据结构，它既可以有较高的插入和删除效率，并且具备较高的查找效率。

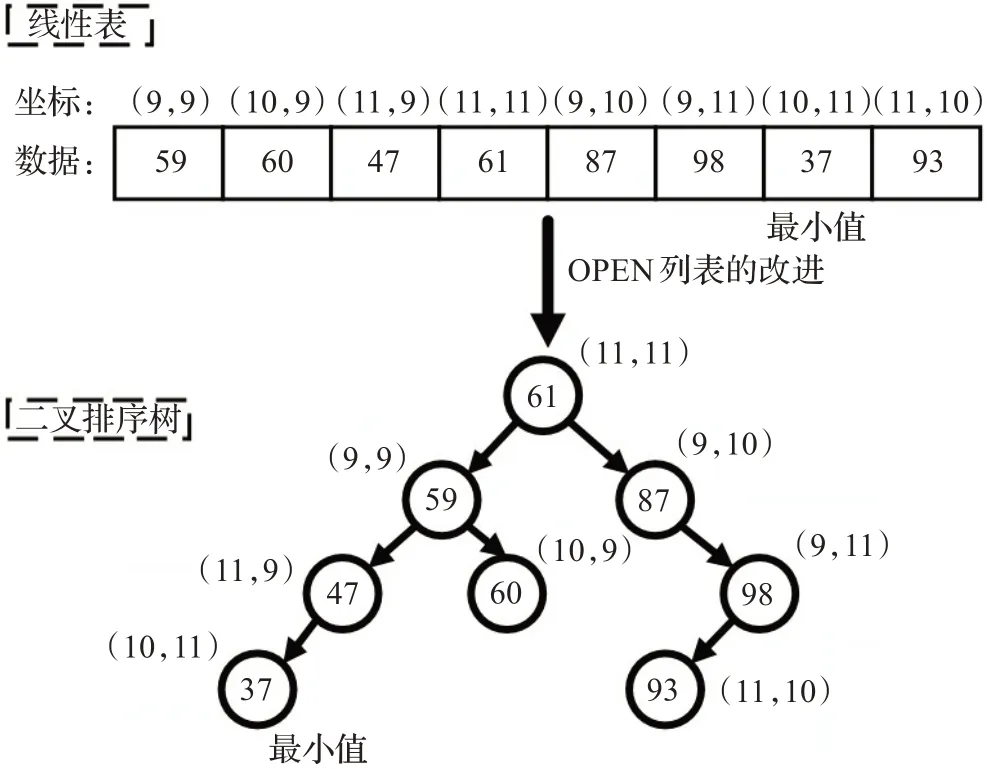
图5 OPEN列表的改进Fig.5 Improvement of OPEN list

树是一种应用广泛的非线性数据结构。二叉树是每个节点最多有两个子树的有序树，它结合了数组和链表的优点，插入、删除和查找的速度很快[16]。二叉排序树是二叉树的一种特殊情况，如图5所示。

数据的最小值存放在整棵树最后一层的最左端，搜索最小值时，只需要遍历整棵树的左子树，也就是说遍历全部节点的一半就能找到最小值。因此，二叉排序树更适合存储ARA*算法中的路径节点数据。

传统ARA*算法在OPEN列表中查找最小值时，用需要查找的数据与线性表中各个数据元素逐个比较，直到成功或遍历结束。假设OPEN列表数据长度为n，那么查找第i个数据元素时需要进行n-i+1次比较，即Ci=n-i+1。又假设查找任意一个数据元素的概率都相同，即Pi=1/n，那么顺序查找算法的平均查找长度表示为公式（4）：

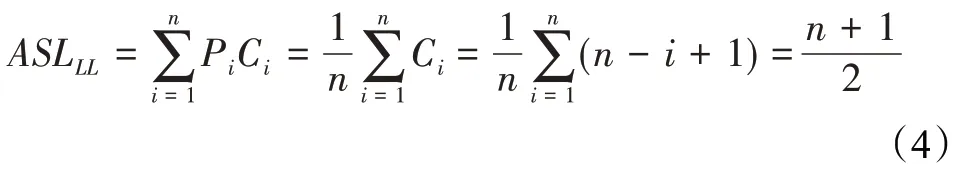
假设一棵满二叉排序树的总节点数是n，高度是h，根节点的高度是1，n与h的关系满足n=2h-1。那么对于高度为h，总节点数是n的满二叉排序树，查找成功时的平均查找长度为公式（5）：

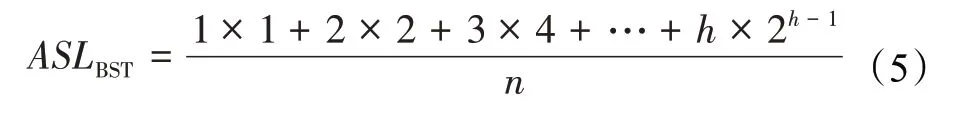
将n=2h-1代入公式（5）计算得到公式（6）：

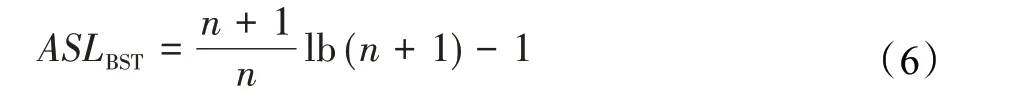
公式（4）和公式（6）的曲线如图6所示，顺序存储结构的平均查找长度随着数据元素的个数呈线性增长，而二叉排序树的平均查找长度按照对数函数的规律增长，其增长速率远远小于顺序存储结构。因此，二叉排序树更适合存储ARA*算法的OPEN列表中的数据。

图6 平均查找长度Fig.6 Average search length

3.2 自适应节点连接方式选择策略

环境地图一般有三种描述方式：栅格地图、几何地图和拓扑地图[17]。在栅格地图中，为了将不同的栅格节点联系起来，需要制定节点间的连接规则，有两种典型的连接方式：4连接和8连接，8连接可能使移动机器人恰巧途经障碍物栅格的顶点，这在实际情况中很危险，但如果只使用4连接，在没有障碍的区域中，过多的折转会增加路径的距离。本文提出了一种自适应的节点间连接方式选择策略，在地图中的不同区域采取更适用于当前局部环境的连接方式。

在启发式函数中，为了计算当前节点到目标节点的距离，首先需要确定节点间的连接方式。本文提出的自适应节点间连接方式选择策略，兼顾了4连接和8连接的优点，当路径经过障碍物的相邻节点发生折转时，为了不穿过障碍物栅格的顶点，采用4连接；当路径的邻域内没有障碍物时切换为8连接，因为没有障碍物时8连接的路径长度更短，折转次数少，路径更平滑。

在改进后的ARA*算法中，计算栅格地图中任意两个节点(ai,aj)和(bi,bj)的h(s)值时，忽略节点之间的障碍物，结合使用两种距离估计的方法：曼哈顿距离和对角距离。曼哈顿距离的计算方法如公式（7）所示：

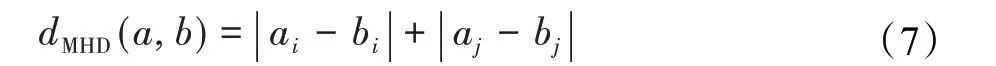
对角距离的计算方法如公式（8）所示：

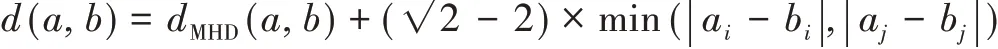
4 仿真实现与结果分析

本章设计了两组仿真对比实验，验证改进ARA*算法的快速性和有效性：

实验1对比传统ARA*算法和改进ARA*算法。

实验2对比蚁群算法、粒子群算法和改进ARA*算法。

为了探究地图规模对算法结果的影响程度，对三种规模的栅格地图进行仿真：50 m×50 m、100 m×100 m和200 m×200 m。栅格地图中的栅格节点有两种形式：有障碍物栅格和无障碍物栅格，机器人经过无障碍物栅格的代价权值为1，栅格地图中的障碍物栅格随机分布。实验平台参数：Win10操作系统；Intel i5-8300H CPU；16 GB DDR4，仿真程序用Python3.7和MATLAB2015b实现。

4.1 传统ARA*算法和改进ARA*算法对比

改进前后的ARA*算法在50 m×50 m、100 m×100 m和200 m×200 m三种规模地图上的仿真结果分别如图7、图8、图9所示。

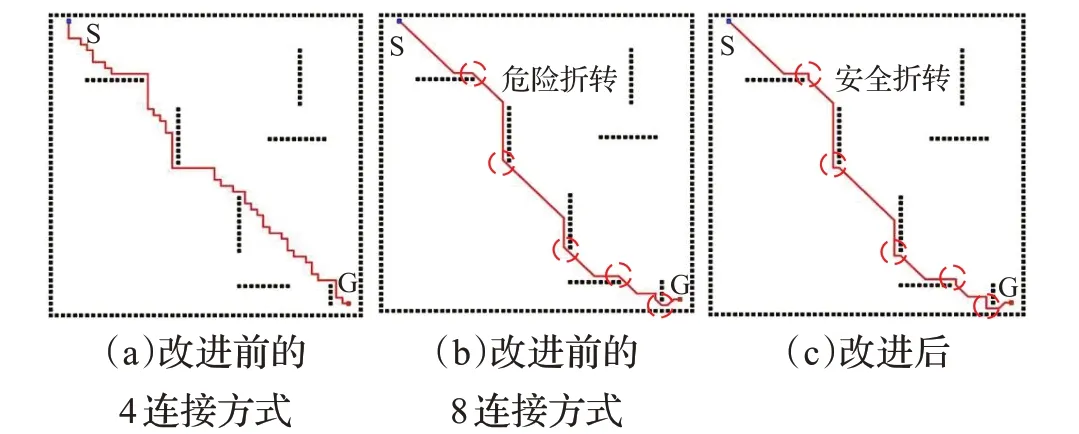
图7 50 m×50 m仿真结果Fig.7 50 m×50 m simulation results

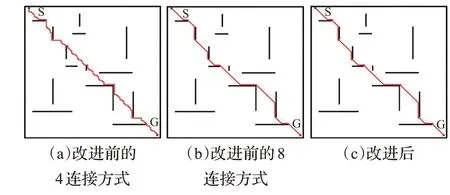
图8 100 m×100 m仿真结果Fig.8 100 m×100 m simulation results

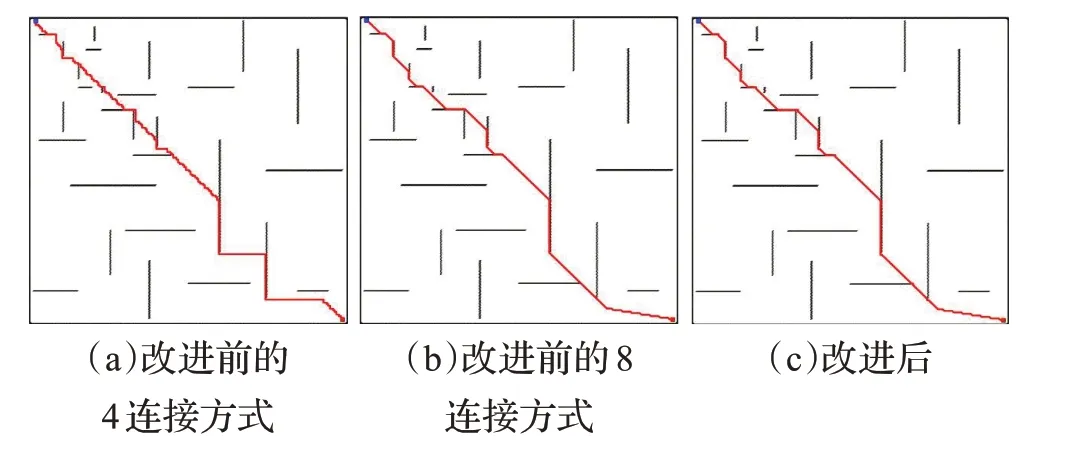
图9 200 m×200 m仿真结果Fig.9 200 m×200 m simulation results

在图7、图8、图9中（a）是改进前4连接ARA*算法的结果，（b）是改进前8连接ARA*算法的结果，（c）是改进后的算法结果。比较（a）、（b）可以看出，传统的4连接ARA*算法的转折次数明显多于8连接，路径长度更长，但是4连接的路径不会从障碍物栅格的顶点穿过，保持了机器人与障碍物之间的距离，因此比8连接更安全。（c）相比（a）和（b）折转次数更少，而且在障碍物处折转时避开了障碍物节点的顶点，兼顾了4连接和8连接的优点，既降低了安全风险，又不会明显增加路径长度。改进前后ARA*算法的搜索时间、路径长度和折转次数如表1所示。

表1 ARA*与改进的ARA*仿真结果Table 1 Simulation results of ARA*and improved ARA*algorithm

从表1中可以看出，在保证栅格地图规模与障碍物设置完全相同的情况下，改进的ARA*算法搜索时间相比于传统的ARA*算法有了明显的缩短；路径长度介于4连接和8连接之间，但明显小于4连接的路径长度；折转次数与8连接相近，远远小于4连接。

根据表2，ARA*算法改进前后的数据对比结果可知，改进的ARA*算法对地图规模不敏感，搜索时间相比改进前平均缩短了43.62%；路径长度相比4连接平均缩短了18%，与8连接的路径长度相近；折转次数相比4连接平均减少了75.2%，相比8连接平均增加了25.4%，对路径平滑性影响不大。结合以上分析得出结论，改进的ARA*算法大幅缩短了搜索时间，并且算法规划出的路径更安全可靠。

表2 改进前后结果对比Table 2 Comparison of results before and after improvement

改进ARA*算法用来存放具有局部不一致状态节点的OPEN列表，从传统的顺序存储结构改为二叉排序树存储，加快了路径节点更新时从OPEN列表中搜索f(s)最小值的速度。为了证明上述理论的正确性，在50 m×50 m的栅格地图中，记录随着路径节点数量累积单次搜索f(s)最小值的时间，结果如图10所示。

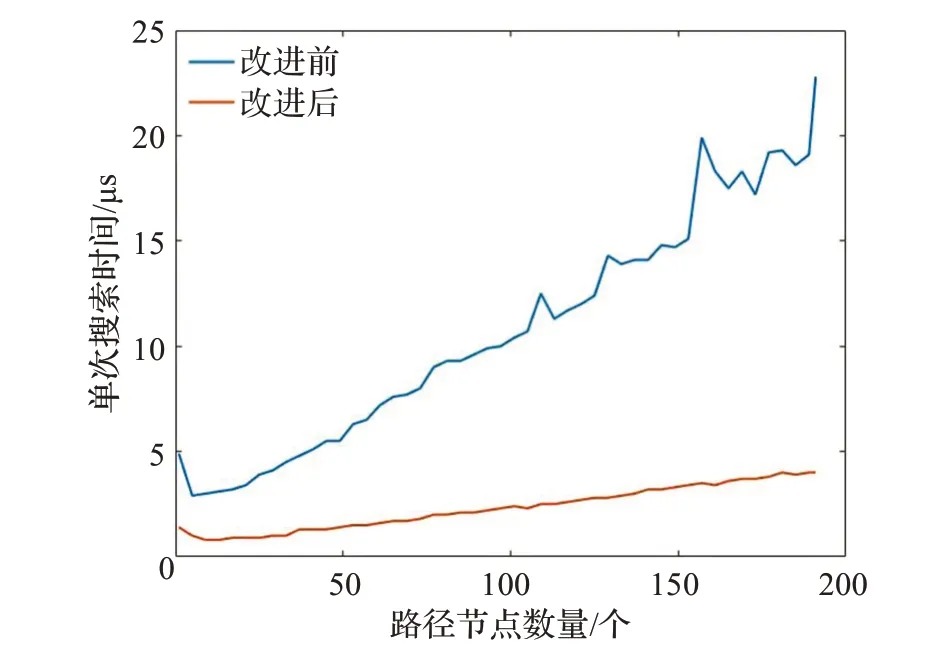
图10 单次搜索时间Fig.10 Single search time

对比图6和图10，因为平均查找长度与单次搜索时间呈正相关，所以单次搜索时间与平均查找长度变化规律相似，增长率数据如表3所示。

表3 单次搜索时间增长率Table 3 Single search time growth rate

由表3可知，改进后时间增长率明显小于改进前，搜索OPEN列表中f(s)最小值的速度大幅提高，证实了用二叉排序树代替顺序存储结构可以提高算法执行效率。效率提升的根本原因是，在数据个数相同的情况下，二叉排序树搜索最值的平均查找长度小于顺序存储结构，比如根据图6，有100个数据元素时，顺序存储结构需要查询50个数据元素，而二叉排序树只需要查询不到10个。

随着数据个数越来越多，改进前平均查找长度呈线性增长，增长率不变，而改进后的曲线呈对数规律增长，增长率越来越小，可见地图规模越大，改进ARA*算法执行效率高的优势越明显。

4.2 蚁群、粒子群算法和改进ARA*算法对比

本节通过仿真实验，对比改进ARA*算法与蚁群算法、粒子群算法，进一步验证改进ARA*算法的快速性和有效性。蚁群算法的参数设置如表4所示，粒子群算法的参数设置如表5所示，三种路径规划算法的仿真结果如图11和表6所示。

表4 蚁群算法参数设置Table 4 Parameter setting of ACA

表5 粒子群算法参数设置Table 5 Parameter setting of PSO

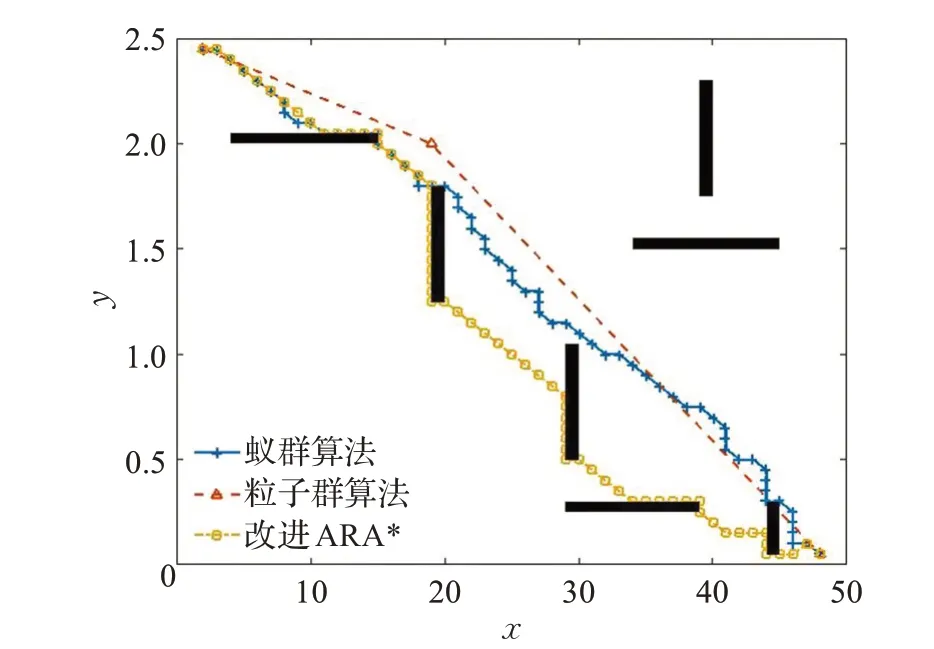
图11 50 m×50 m地图三种算法的路径Fig.11 Path of 3 algorithms on 50 m×50 m map

图11和表6的仿真结果反映出，相比仿生智能算法，改进ARA*算法执行速度更快。改进算法的路径长度比粒子群算法多出11%，这是因为改进的ARA*算法为了保证算法的快速性，启发函数中的膨胀因子ε>1，因此没有计算出路径的最优解，但是多出的路径长度仍可以接受。对于传统蚁群算法，它的启发信息较弱，在路径搜索时转折点较多，有时出现回环交叉，远离目标行走，导致路径长度增加。粒子群算法的路径最短，折转次数仅有1次，路径最平滑，因为粒子群算法是概率型的全局路径规划算法，在迭代的过程中充满更多可能性，搜索路径过程中能覆盖全局地图的机会更大，因此更能够得到全局最优解[18]，但是算法运行时间过长，不适合解决实际工程问题。

表6 三种算法的仿真结果Table 6 Simulation results of 3 algorithms

5 结束语

由于传统的ARA*算法不能满足移动机器人对实时性和安全性的要求，本文利用二叉排序树代替顺序存储结构，降低了节点更新时每次从OPEN列表中搜索最值的时间，优化了路径规划时数据查找的效率，搜索时间缩短了43%；另外，提出了自适应的连接方式选择方法，改善了了机器人移动的安全性。实验结果证明，改进的ARA*算法为移动机器人路径规划问题提供了一种可行的解决方案，一定程度上推动了路径规划算法的发展。