基于LSTM-RPA音乐流行趋势预测研究

李 堃，李 猛，李艳玲，林 民

内蒙古师范大学 计算机科学技术学院，呼和浩特 010022

随着网络技术发展，流媒体应用之一的音乐应用也得到了快速发展，先后出现诸如QQ音乐、酷我音乐、阿里音乐、网易云音乐等应用软件。人们在线试听、分享、下载、收藏、发表评论交流音乐感想的同时，会在服务器上产生大量的用户行为数据，包括歌曲名、艺人、曲风、播放时长、播放次数等。这些数据不仅对生成用户画像有影响，也对艺人曲风变化具有指导作用。早期研究大多数集中在通过分析音乐播放列表[1]、音乐特性（和声、节奏、音色和情绪）[2]、音乐语义结构（流派、感情、乐器和主题）[3]为用户精准推送音乐。而通过分析大量艺人及用户行为数据对音乐流行趋势进行预测的研究仍处于早期。

阿里音乐经过多年发展积累了数百万的曲库资源、数以亿计的用户行为数据。并在2016年，通过天池大数据平台举办了“阿里音乐流行趋势预测大赛”。该比赛是第一个对音乐流行长趋势预测的比赛，参赛选手需要利用给定的6个月数据，预测未来2个月的艺人每日音乐播放量。从而实现对潜在热门艺人的挖掘。而当前大多数研究主要集中在短趋势预测，对长趋势预测误差仍然较大。这是因为现有模型在预测长达30天以上的数据时，预测波动会在短时间内变为一个恒定值。这给长趋势预测带来了极大的挑战。

传统的时间序列模型由于历史信息在模型中逐渐衰减，因此无法在长序列（趋势）预测中获得较高的性能。而深度神经网络可以学习序列中潜在的序列波动信息以及周期信息，但仍面临历史信息衰减的问题。因此，针对该问题，本文基于循环神经网络提出具有不同特性的长短期记忆滚动预测模型（long short-term memory rolling prediction algorithm，LSTM-RPA）。通常来说，研究人员认为已训练的模型是含有数据的高维抽象信息。基于此，RPA算法利用模型已学习的高维信息指导模型进行滚动预测，即在预测阶段将前一次输入与当前预测结果相结合作为下一次预测的输入，使得历史信息可以沿模型指导的预测方向流动，从而缓解模型内部带来的长趋势信息衰减。实验结果证明：在长趋势预测中，LSTM-RPA相比于基于循环神经网络的模型，预测性能有较大的提升。

1 相关工作

早期，时间序列建模主要采用人工规则、回归模型、自回归滑动平均模型（auto regressive moving average，ARMA）[4]、差分整合滑动平均自回归模型（auto regres‐sive integrated moving average，ARIMA）[5]。ARMA与ARIMA模型常用于周期性平稳序列预测，但无法应对具有复杂周期波动的长序列预测任务。

随着人工智能技术的发展，深度神经网络逐渐应用在音乐流行趋势预测中。Salganik等人通过建立人工音乐市场（artificial“music market”），发现一首获得成功的音乐不仅与其本身质量有关，也与社会偏好有关[6]。这种外部影响因素的不确定性极大增加了音乐流行走势预测的难度。吕倩倩通过建立人工神经网络（artifi‐cial neural network，ANN）和支持向量机（support vector machine，SVM）的组合模型，与SVM回归预测模型相比，在预测未来30天播放量的任务中均方误差（mean square error，MSE）降低12.90%[7]。但该组合模型难以应对突增的数据波动以及周期较长的数据。颜家康提出使用BP（back propagation，BP）神经网络对音乐流行趋势进行预测，他们采用5天真实播放量数据预测未来1天的播放量，然后“滑动”预测30次得到30天的预测结果。BP神经网络的预测结果与二次平滑法、ARIMA模型相比平均相对误差率分别减少2.81%和3.4%[8]。实验证实BP神经网络在短时间序列预测中具有较高的性能，但仍然难以应对长时间序列预测。

郁伟生等人首先将艺人音乐播放量的时序特征通过编码分为基本趋势编码和增量趋势编码。基本趋势编码采用one-hot编码，1代表上月均值大于当月均值，反之为0。增量趋势编码则将当月均值和上月均值相比取整得到两月之间的倍数关系。之后采用k-means聚类算法的方式将艺人分为24个类别。然后通过基于类别最优值选择法的音乐流行趋势预测算法（time series music prediction，TSMP），循环遍历候选预测算法集得到最优结果。但当艺人播放量突然成倍增加时会使TSMP模型预测准确度降低，因此提出结合子序列模式匹配法（sub-sequence pattern matching method，SSPMM）和附加处理（additional processing，AD）的扩展音乐流行趋势预测算法（extend-time series music prediction，E-TSMP）来进一步提高预测精度。具体的，先从其他艺人数据中寻找类似的突变趋势，然后计算之间的欧式距离，最后从距离最小的5个曲线数据中选择变化趋势最平稳的数据作为预测结果[9]。他们提出的算法在比赛复赛中获得亚军，但该算法没有考虑具有周期性叠加变化的序列，以及无法学习序列中隐含的趋势变化信息。同时，该算法依赖人工数据清洗，难以在更复杂的场景中应用。

在深度学习中，循环神经网络（recurrent neural net‐work，RNN）可以很好地从序列中提取并记忆关键信息。但由于RNN网络的结构缺陷会导致历史信息在反向传播中丢失，并出现梯度消失和梯度爆炸的问题。因此，Hochreiter对RNN网络进行改良后，提出长短期记忆（long short-term memory，LSTM）神经网络[10]，该模型可以有效解决RNN在长序列中的梯度爆炸和梯度消失问题。这也使得LSTM相比于RNN更加适用于时间序列预测任务。Yu等人在音乐趋势预测中比较了SVM与LSTM模型，结果显示采用前9天的数据预测未来1天的情况下，当模型的输入特征一致时，SVM模型比LSTM的预测准确度高1%[11]。王振业等人采用LSTM和Attention机制的组合模型预测音乐流行走向，他们在2层LSTM层后增加注意力机制，使得LSTM的每一个神经元可以获取来自其他神经元的交互信息。在采用3天真实数据预测未来1天的情况下，该模型相比LSTM和SVM均方根误差分别减少0.027和0.013[12]。

综上，当前鲜有对音乐流行长趋势的研究，其难点是在单次预测长达15天以上时，模型中的历史信息会在短时间内完全衰减。本文在分析现有时间序列模型和神经网络后，发现在模型预测阶段将历史信息引入可以有效缓解历史信息衰减的问题。因此，本文提出基于LSTM的滚动预测算法，该算法将预测模型t-1时刻的部分输入与t时刻的预测结果组合，从而缓解历史信息在模型中的衰减。在预测艺人8月每日播放量的实验中，与传统时间序列模型：ARIMA模型、简单移动平均（simple moving average，SMA）模型[13]和多种循环神经网络模型：LSTM、双向长短期记忆网络（bidirectional long-short term memory，BiLSTM）[14]、门控循环单元（gated recurrent unit，GRU）[15]、RNN模型相比，预测精确度均有较大的提升。

2 基于长短期记忆网络的滚动预测模型

随着深度学习的发展，研究人员大多采用循环神经网络对时间序列建模，以提高在短趋势预测中的准确性。当前文献大多采用如下两种方式预测：（1）模型直接输出长度为预测天数的长趋势预测结果，（2）每次预测采用3~5天的真实数据作为模型输入以预测未来1天的趋势，然后“滑动”预测30或60次，作为最终预测30天或60天的结果。但这种预测方式仍然是短趋势预测，所提出的模型并不能真正预测长趋势。

上述预测方式在对长趋势预测建模中，历史信息会因预测时长的增加而快速衰减。因此，在长趋势预测中，本文提出针对滚动预测算法的可复用LSTM模型。代码：https：//github.com/maliaosaide/lstm-rpa。

2.1 可复用LSTM模型

艺人音乐每日播放量预测可以看作是时间序列预测任务。而LSTM在克服了RNN的缺陷后，更擅长应对时间序列预测任务。LSTM网络通过使用三种门控机制（遗忘门、输入门以及输出门）控制历史信息的流动，通过时间反向传播（back-propagation through time，BPTT）进行训练，使模型准确学习到时间序列之间的信息[10]。

设时间序列X={x1,x2,…,xn}，x1,x2,…,xn表示每一个时间点，其中包含该时间点的特征信息。LSTM块中遗忘门ft通过Sigmoid函数激活上一层隐状态ht-1和当前输入状态xt，该激活值在[0,1]之间。公式如式（1）所示：

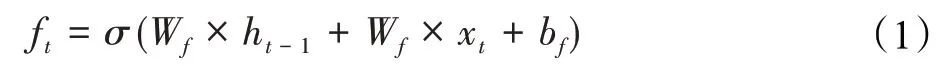
输入门it则是控制当前层哪些信息作为新增记忆加入当前记忆状态Ct,it同样由Sigmoid函数激活上一层隐状态ht-1和当前输入状态xt生成，但权重与ft的权重不同。公式（2）、（3）所示：

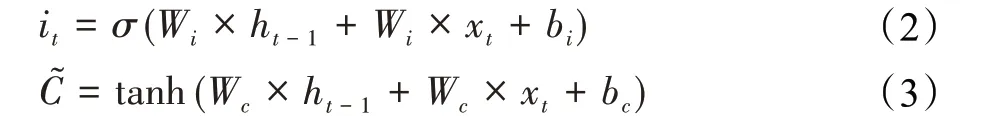
记忆状态更新是通过ft控制的上一层历史记忆状态Ct-1与it控制的新增记忆C共同生成当前记忆状态Ct，公式如式（4）所示：

最后，当前层隐状态ht由tanh函数激活记忆状态Ct以及输出门ot共同生成。公式如式（5）、（6）所示：

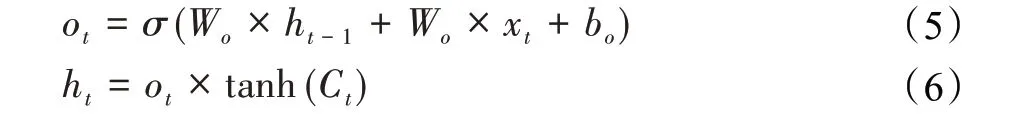
在模型训练结束后，除了隐藏状态会记忆一部分历史信息，记忆状态还会记忆整个序列的高维隐信息，诸如序列的变化率、衰减率等信息。

2.1.1 单特征LSTM模型

通常来说，与当前艺人音乐播放量最为相关的特征就是该音乐的历史播放量。因此，将该特征作为首选特征，并建立如图1所示单特征LSTM模型（single-feature LSTM，SF-LSTM），该模型由输入层输入不同时间步长的时间序列数据，经过分别由64和32个神经元构成的2层LSTM层，并使用ReLU作为激活函数，以减少信息丢失。同时，设置第一层LSTM的记忆状态传递到第二层LSTM。之后采用全连接层将最后的LSTM层的神经元线性组合，使输出维度与输入维度一致。图1中p为输入时间步长，用于控制输入长度，q为输出时间步长，用于控制输出长度，hinit为初始隐状态。

图1 单特征LSTM模型Fig.1 Single feature LSTM model

2.1.2 多特征LSTM模型

除上述所提出的音乐历史播放量特征外，音乐流行趋势还可能受其他相关特征影响，诸如：周播放量均值、月播放量均值、下载量、收藏量等。本文建立如图2所示的多特征LSTM模型（multi-feature LSTM，MF-LSTM），该模型由3层LSTM层构成，前2层同样是由64和32个神经元构成的LSTM层，ReLU作为激活函数。同时，为了减少特征之间的直接相互作用和影响，输出层并没有采用全连接层进行输出，而是采用LSTM层直接输出，其输出步长为q，Sigmoid作为激活函数。

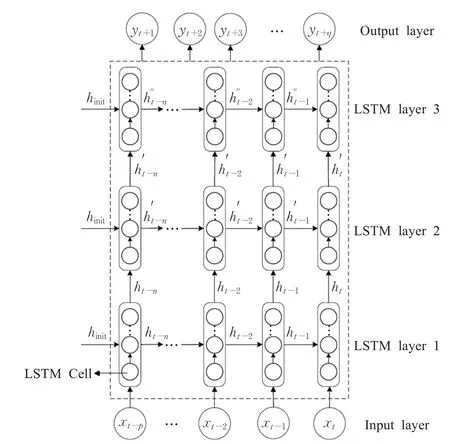
图2 多特征LSTM模型Fig.2 Multiple features LSTM model

2.2 滚动预测算法

在音乐趋势预测中，现有的模型大多采用第二种预测方式，即采用真实数据，在短时间预测1天，然后“滑动”预测30~60次。无法真正用于长趋势预测。而第一种预测方式则会带来极大的误差，在长趋势预测中无法应对长尾效应和历史信息衰减。

LSTM在训练后，记忆状态仍然含有整个序列的高维信息，该信息可以在多次预测中指导模型，从而缓解时间序列模型在长趋势预测中历史信息衰减严重的问题。因此，本文提出滚动预测算法（rolling prediction algorithm，RPA）使得历史信息可以沿预测方向流动。具体描述为：已训练的可复用模型具有相同的输入和输出，然后将模型前一次的部分输入和当前输出序列组合作为模型预测下一个时间段的输入序列。

RPA考虑将一个时间步长为T的序列转化为多个长度为p的预测任务。算法在构建模型预测t+1时刻的输入数据，将t-1时刻和t时刻的信息共同引入，使得模型在t+1时刻的预测中既考虑t-1时刻数据也考虑t时刻的数据。算法如公式（7）、（8）所示：

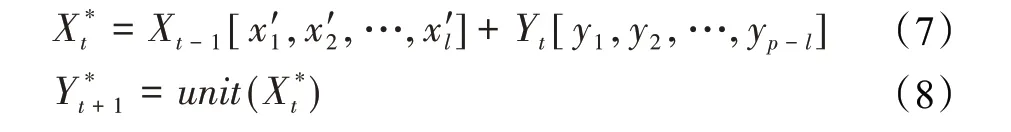
设模型的输入序列X长度为p，输出序列Y长度为q，l为滚动步长，则有0≤l≤p,0≤p-l≤q。式（7）中Xt-1是模型预测t时刻的输入序列，从中倒序选取l个输入值x'1,x'2,…,x'l。Yt是模型预测t时刻的预测结果，从中正序选取p-l个预测值y1,y2,…,yp-l。则预测t+1时刻模型输入序列X*t由Xt-1和Yt共同构成。式（8）中，unit为已训练好的序列神经网络，组合序列X*t通过unit得到预测结果Y*t+1。

将SF-LSTM和MF-LSTM作为unit，构建LSTM滚动预测模型，模型结构如图3所示。其中xt,xt-1,…,xt-p为t-1时刻的输入；yt+1,yt+2,…,Yt+q为t时刻的预测结 果 。 模 型 预 测t+1时 刻 的 输 入X*t由Xt-1[x'1,x'2,…,x'l]和Yt[y1,y2,…,yp-l]序列共同组合而成，然后通过训练后的LSTM模型得到t+1时刻的预测值Y*[Y*t+1,Y*t+2,…,Y*t+n]。对于单特征数据，每一个x∈Rl×1,y∈R(p-l)×1。对 于 多 特 征 数 据，每 一 个x∈Rl×feature,y∈R(p-l)×feature,feature为特征数量。

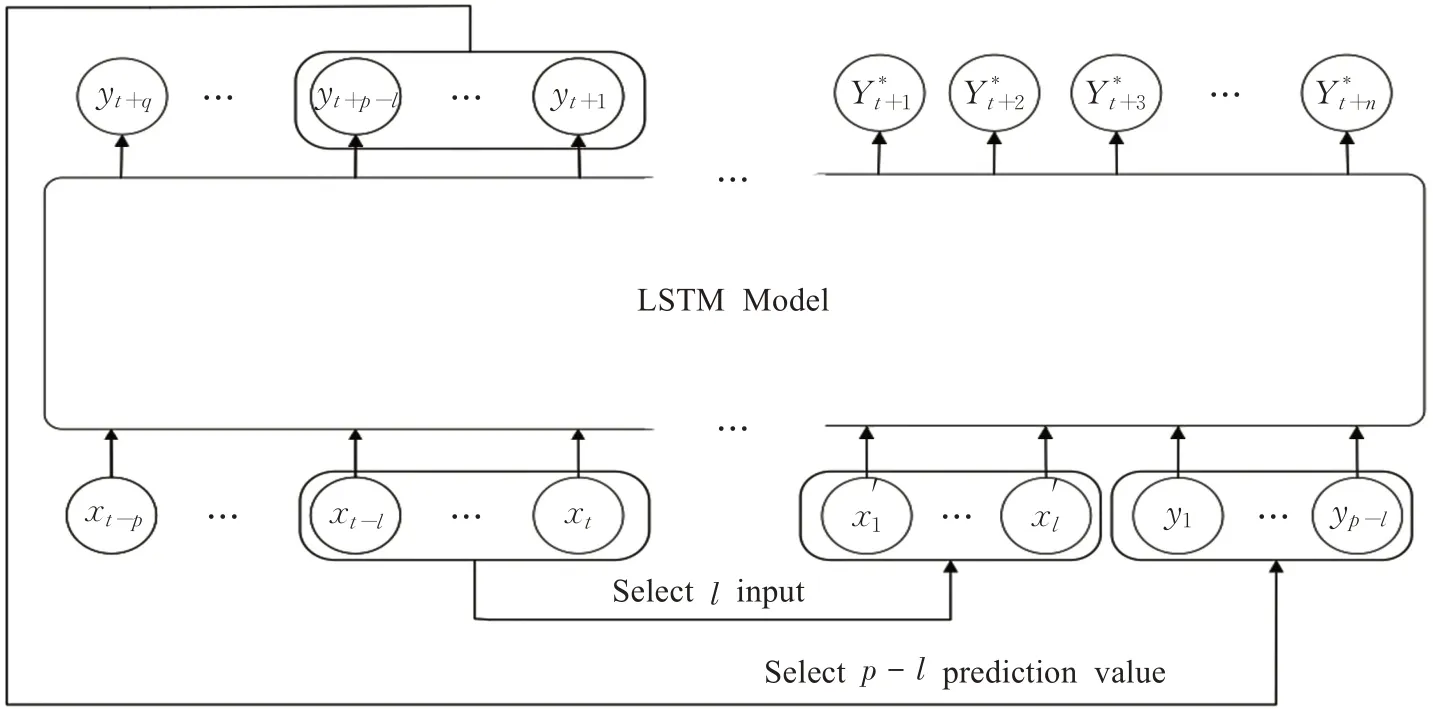
图3 LSTM滚动预测模型Fig.3 LSTM rolling prediction model

3 实验

3.1 数据准备与分析

数据集来自“2016年阿里音乐流行趋势预测大赛”，该数据集自2015年3月1日到8月30日共计183天，50位艺人，349 946位用户，10 842首歌曲（数据集：https：//tianchi.aliyun.com/competition/entrance/231531/informa‐tion）。数据经脱敏处理后发布，即使用长度固定的字符串来代替歌曲名、艺人名、用户ID；歌曲与艺人唯一对应，即一首歌曲只属于一位艺人。数据格式如表1和表2所示。

表1记录了用户行为，如曲目名称、所属艺人、操作记录日期、对歌曲操作类型。表2记录艺人与歌曲对应关系，如歌曲所属艺人、歌曲语种、初始播放量。在对数据集预处理后发现1位艺人数据缺失严重，为保证最后得分的准确性，实验选择其余49位艺人数据作为最终实验数据。并且考虑到不同特征对模型的影响，本文设计了两个对比实验，即单特征和多特征实验，并选择艺人每日歌曲播放量作为单特征实验的输入特征，选择艺人每日歌曲播放量、下载量、收藏量作为多特征实验的输入特征。同时，将3月至7月数据集以122∶31进行切分作为训练集与开发集，将8月份数据作为测试集。

表1 用户行为Table 1 User action

表2 歌手与歌曲信息映射表Table 2 Relations between artists and songs

3.2 艺人歌曲播放量趋势分析

图4展示了从49位艺人中随机抽取的4位艺人3月到7月的每日播放量趋势。艺人A前40天播放量波动幅度较大，40天后逐渐稳定在每日1 000左右的播放量；推测前40天可能是该艺人发布新专辑后的推荐期，也可能是该艺人制作的当季热门电视剧、电影插曲。艺人B总播放量趋势呈抖动上升，30天后有近10天的高速增长期，这期间可能受外部平台推荐或同类歌曲推荐影响；80天后播放量趋势呈波动缓慢上升。艺人C前70天播放量趋势平稳但在第75天时数据出现跳跃式增长，对此有如下猜测：（1）该数据为错误数据。（2）增长与特殊节日有关。（3）受轰动性娱乐新闻影响。艺人D的每日播放量极不稳定但总趋势平稳。

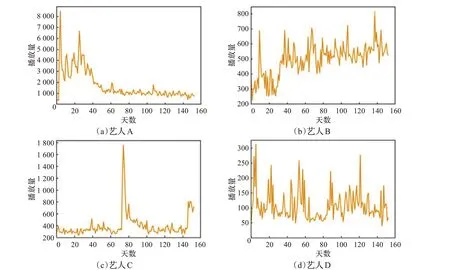
图4 3~7月艺人A、B、C、D的歌曲播放量趋势Fig.4 From March to July，trend of songs played by artists A，B，C，D

综上所述，由于每一位艺人的历史播放量数据都含有独特的时间信息，而且数据区间差距较大，无法使用同一个模型进行预测，因此本文对每位艺人单独建立音乐趋势预测模型。

3.3 评估指标

比赛主办方给出了量化音乐趋势预测准确度的评估函数。设艺人a,a∈W,W为艺人集合，其在第d天的真实播放量为Ya,d，预测播放量为Xa,d，则艺人a归一化方差σa可由如下公式求得：

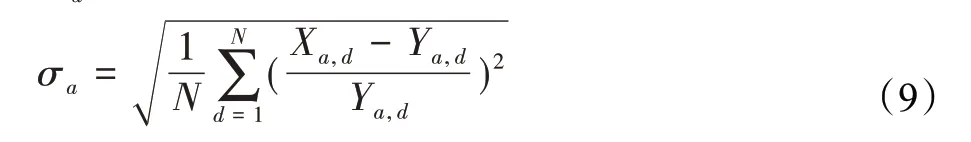
式（9）中N为预测的总天数，σa表示预测值Xa,d与真实值Ya,d之间的差距，σa越小则(1-σa)越大，表示预测越准确。艺人权重∅a由每日真实播放量求和后的算术平方根表示，如式（10）所示：

最后定义评估函数F：

本文将评估函数F作为衡量预测准确度的标准，F值越大则预测越准确。

4 实验结果

艺人歌曲播放量趋势不仅受不同特征的影响，也受滚动步长与时间步长不同的影响。实验探究了在单特征与多特征下不同滚动步长与时间步长对长趋势预测准确度的影响。实验使用Keras框架编写，设置输入步长与输出步长相等，并在相同条件下进行多次实验。

4.1 基于单特征的滚动预测实验

实验对LSTM、BiLSTM、GRU、RNN这4种神经网络建立模型并进行对比。其中GRU、RNN的网络结构与前文提出的SF-LSTM模型的网络结构一致，BiLSTM模型将前两层LSTM层修改为双向LSTM层，即数据仅在当前双向LSTM层进行正向和反向流动。基准线（黑线）则采用结构相同的模型直接预测30天的结果。实验只考虑得分为正数的情况，对得分为负进行归0处理。

图5展示了在单特征情况下，不同的滚动预测模型在不同输入时间步长与滚动步长下对49位艺人的预测F值总分。当输入时间步长小于3时，LSTM-RPA模型的预测准确度优于未使用RPA的LSTM模型。但当输入时间步长大于3时，该模型由于出现过拟合现象导致预测准确度大幅降低。BiLSTM-RPA模型在前4个时间步长中，只有当输入时间步长与滚动步长为2时出现欠拟合情况（F值为276.951 4），其余预测得分均高于基准线；同时在输入时间步长为4时，不同的滚动步长对预测准确度有不同的影响，且随着滚动步长的增加准确度也不断提升。GRU-RPA模型作为LSTM-RPA模型的一种变体，在输入时间步长小于3时同样有较高的预测准确度。在输入时间步长大于3时相比于LSTM-RPA模型，GRU-RPA模型仍有一定的预测精度（滚动步长4）。RNN-RPA模型在前5个输入时间步长的预测得分均超过基准得分。

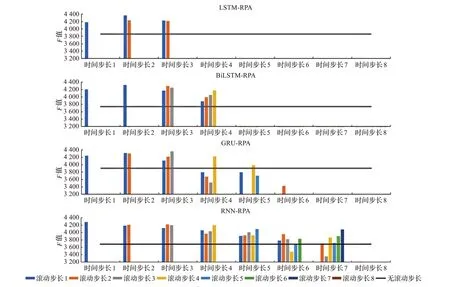
图5 单特征实验中不同RPA模型预测得分Fig.5 Prediction scores of different RPA models in single feature experiment

4.2 基于多特征的滚动预测实验

由于歌曲播放量趋势不仅与歌曲历史播放量有关，还与歌曲下载量、收藏量有一定的关系。本实验使用历史播放量、下载量、收藏量作为模型输入特征，并探究不同输入时间步长与滚动步长对各种模型的影响。在单特征实验的基础上对上文的4种神经网络进行修改。

GRU、RNN的网络结构与前文提出的MF-LSTM模型的网络结构一致。BiLSTM模型的输出层为单向LSTM层，其余为双向LSTM层。基准线采用结构相同的模型直接预测30天的结果。

图6展示了多特征实验下不同时间步长与滚动步长下不同模型的预测得分。在增加特征数量后，LSTMRPA模型在8个不同的输入时间步长下预测准确度均高于未使用RPA的LSTM模型。BiLSTM-RPA模型在输入时间步长大于5时，其预测准确度随着输入时间步长的增加而减少。这是因为随着输入时间步长的增加，参与模型训练的数据量也在增加，同时在双向网络结构中，网络的正向和反向会导致训练数据的增加，使得模型再次巩固非关键数据的记忆，从而导致预测准确度的降低。在GRU模型实验中，GRU-RPA模型的基准预测得分高于其他实验的基准模型。但RPA对基准GRU模型仍有优化作用。RNN-RPA模型的预测准确度在相同时间步长下，受不同滚动步长的影响较大，但仍然有部分预测准确度高于基准线。

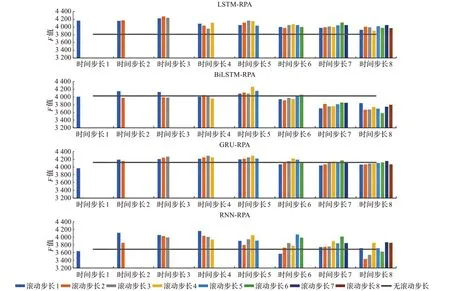
图6 多特征实验中不同RPA模型预测得分Fig.6 Prediction scores of different RPA models in multiple features experiment

5 实验分析

实验探究了在不同特征数量下，时间步长数与滚动步长数对RPA的影响。最终选取不同特征下各滚动模型的最优F值及基准线进行对比。表3展示了单特征实验下不同滚动预测模型的最优值与基线得分。在4种模型中SF-LSTM-RPA模型的预测得分最高，且平均误差低于其他模型。同时，SF-GRU-RPA模型与SFLSTM-RPA模型的预测得分差距极小。并且，RPA对RNN模型的预测准确度提升效果优于其他模型，其次是BiLSTM模型。该实验发现在单特征条件下本文提出的RPA对这4种模型均有超过10%的优化效果，证明RPA算法在单特征长趋势预测中对序列神经网络有一定的优化效果。

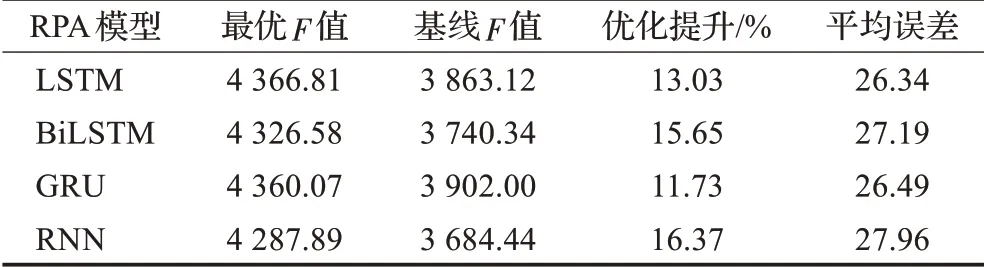
表3 单特征实验中各模型最优F值和基准线Table 3 Optimal F value and baseline of each model in single feature experiment

表4展示了多特征实验中不同滚动预测模型的最优F值与基线得分。其中LSTM-RPA、BiLSTM-RPA、GRU-RPA这三种滚动预测模型的最优预测得分差距不大。但分别与各自基准线相比，RPA对LSTM模型的优化提升占比最高，但略逊于对RNN模型的优化效果。同时GRU-RPA模型的预测准确度优于其他模型，且具有最低的平均误差，并且该模型的基准线也优于其他模型。该实验表明，在多特征实验下本文提出的RPA算法仍然对这4种模型有超过4%的优化效果。

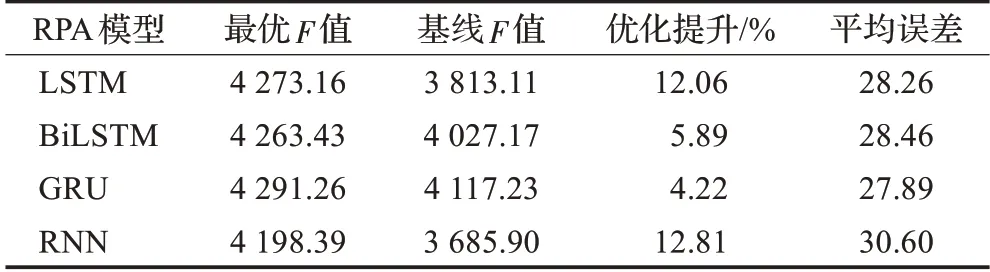
表4 多特征实验中各模型最优F值和基准线Table 4 Optimal F value and baseline of each model in multiple features experiment

在单特征及多特征实验的基础上，本文选取预测准确度最高的RPA模型（SF-LSTM-RPA）与不同的基准模型以及传统时间序列预测模型：ARIMA模型、SMA模型进行对比。表5展示了传统时间序列预测模型、RPA模型以及基准模型的最优F值和平均误差情况。实验结果表明SF-LSTM-RPA模型的预测准确度优于其他模型，与ARIMA模型、SMA模型相比F值分别提高10.67%、3.43%，同时平均误差分别降低32.64%、11.23%，平均误差方差分别降低368.73%、35.29%；与LSTM模型、BiLSTM模型、GRU模型、RNN模型相比F值分别提高13.03%、16.74%、11.91%、18.52%，平均误差分别降低39.02%、48.55%、36.02%、52.88%，平均误差方差分别降低183.69%、252.83%、175.23%、225.79%。

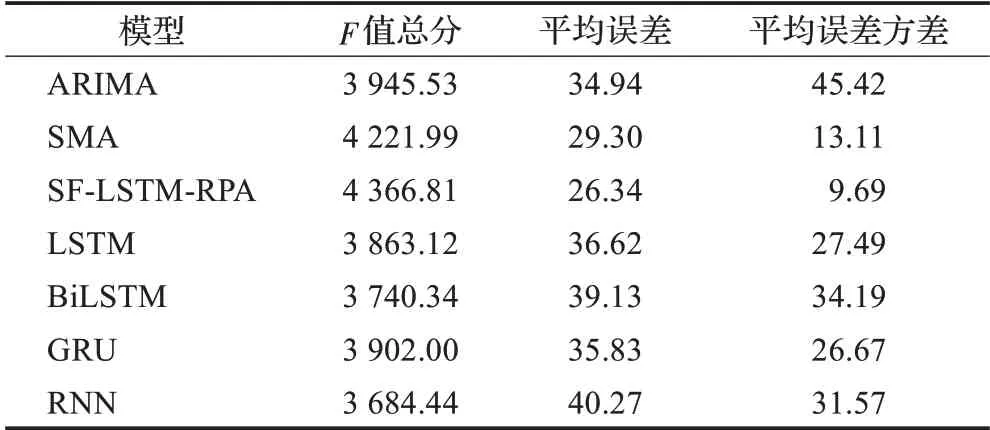
表5 各模型的最优F值和平均误差Table 5 Optimal F values and mean errors of each model

综上，实验发现LSTM-RPA在单特征实验中具有较高的预测准确度，并且与多特征实验相比单特征实验的平均相对误差更低。在算法优化提升占比中，RPA算法对多特征实验的优化效果略低于对单特征实验的优化效果。同时与传统时间序列预测算法相比，SF-LSTMRPA模型具有更高的预测准确度。在平均误差方差的比较中，SF-LSTM-RPA模型与LSTM模型相比具有更低的方差，这也证明本文提出的RPA在长趋势预测任务中对神经网络模型具有一定的优化效果。最终实验结果显示，在长趋势预测任务中，通过RPA复用模型可以有效缓解随着预测序列增加所带来的历史信息衰减问题。

6 总结

在时间序列预测中，长趋势预测建模一直是研究的重点和难点。在对音乐流行长趋势预测任务的建模中，为了解决模型在长趋势预测中历史信息衰减严重的问题，本文提出一种基于LSTM的滚动预测模型。该模型利用已训练的LSTM模型中记忆状态含有的高维序列信息的特点，在构建模型预测t+1时刻的输入序列时，将t-1时刻和t时刻的信息共同引入，使得历史信息在预测中进一步传递，从而缓解在音乐长趋势预测任务中历史信息衰减的问题。实验证明在音乐长趋势预测中，SF-LSTM-RPA模型的预测准确度要优于传统的ARIMA模型和SMA模型，且总F值分别提高10.67%、3.43%，同时平均误差分别降低32.64%、11.23%。该模型与深度学习序列模型LSTM、BiLSTM、GRU、RNN相比F值提高13.03%、16.74%、11.91%、18.52%，平均误差减少39.02 %、48.55%、36.02%、52.88%。

时间序列预测是近几年对多个行业都有重要研究意义的课题。大数据时代下，许多互联网公司通过对用户行为分析后提供歌曲推荐、广告精准投放、搜索结果优化等个性化服务。长趋势预测研究可以挖掘网络潜在热点，进而为公司的决策及发展方向提供帮助。

未来在该研究的基础上还可以进行的工作：模型超参数无法随着艺人的不同而改变，导致部分艺人模型在训练中出现欠拟合现象，且时间步长与滚动步长的不同组合对预测结果具有一定的影响。在后续研究中，针对滚动步长、时间步长加入Attention机制来建立自适应LSTM滚动预测模型。