β扰动的随机SI系统的渐近行为

刘振文

(吉林建筑科技学院 基础科学部， 吉林 长春 130114)

0 引 言

数学建模已经成为分析传染病流行和控制的重要工具，大多数传染病模型都来源于经典的Kermack W O等[1]SIR模型，与已感染者个体接触后易感染者成为已感染者。最近，生态流行病学模型已引起人们注意力。相关文献非常多，为方便起见，我们只提一篇述评[2]和几本书[3-4]，假设所研究种群与其他种群没有联系，也就是说，这些传染病模型只用来描述一种传染病的传播，很多学者得到了阈值理论。

在自然界里种群并不单独存在，当其他种群传播疾病时，这个种群也与其他种群争夺生存空间和食物，或者被其他种群捕食。因此，当我们研究生态流行病学的动力学行为时，考虑种群间的相互作用具有重大的生物意义。目前为止，把这两个领域联系起来的研究还很少。文中首先介绍捕食者基于最经典的生态流行病学模型，即SI模型，以研究捕食者的行为对传染病的影响。为此，只研究最简单的情形，即捕食者只吃有病的食饵，这与实际情况是相符的，有病的食饵相对来说缺少活力，更容易被捕食者捕获。或者说有病食饵的行为被迫发生改变，以至于活动在更容易被捕获者捕获的区域。例如，鱼和水生蛇停留在更靠近水面的位置，蛇停留在植物的顶端而不是被植物覆盖。Xiao Y等[5]提出，当老鼠遭受细粒棘球绦虫疾病时，狼捕获老鼠成功率更大。

这样就得到两个种群：N表示食饵种群的总密度；Y表示捕食者种群的总密度。

我们做如下假设:

1)在无病条件下，食饵种群的增长符合Logistic规律，环境容纳量为K>0，内禀增长率为常数r>0，则有

2)在有病条件下，食饵种群总数N由两部分组成：一类是易感染者(记作S)，一类是已感染者(记作I)，则有

N(t)=S(t)+I(t)。

3)为方便起见，我们仅假设易感染者S具备繁殖能力，且服从上述Logistic规律。也就是说，已感染食饵I被死亡除去了，即已感染食饵或者已死亡率正常数c>0，死亡或者在繁殖前被捕食者捕获。然而，已感染种群I与S一起对种群的增长有贡献，并使之达到环境容纳量。

4)传染病只在食饵中传播并且不遗传。已感染者不会康复或者获得免疫力。考虑最简单的大范围行为发散率βSI，其中β>0表示转移系数。这样就建立了确定性SI模型：

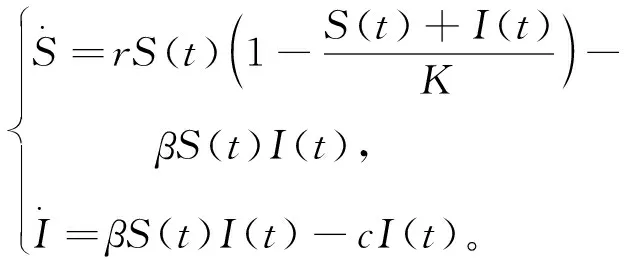
(1)

系统(1)有如下平衡点：

E0=(0，0)，

E1=(K，0),R0<1，

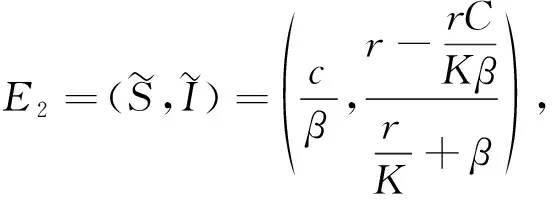
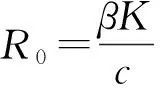
在随机波动和随机扰动情况下，系统(1)受到环境白噪声的影响，性质有何改变?而就作者所知，目前对随机SI系统的研究很少。文中首先对确定性系统(1)进行线性扰动，得到如下系统[7]：

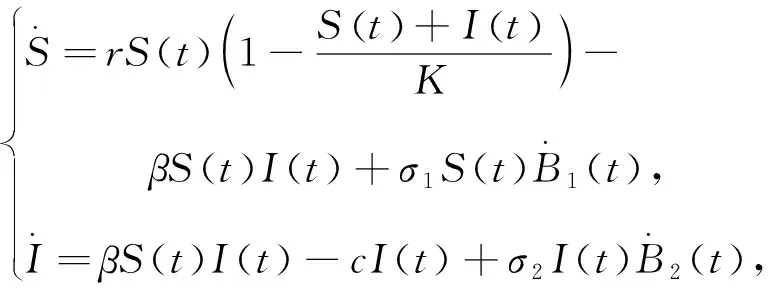
(2)

式中：Bi(t)----相互独立的布朗运动，i=1，2;

σi----正的常数;

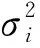
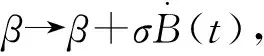
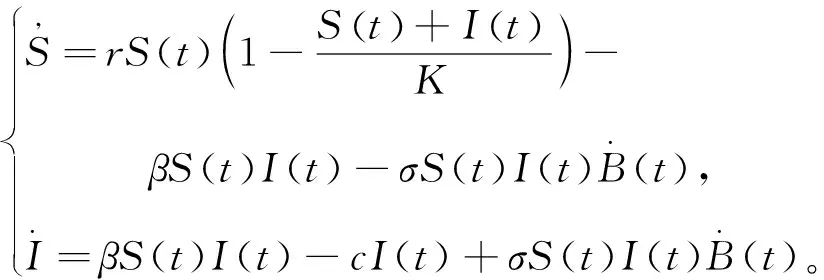
(3)

接下来用随机分析理论研究系统(3)的随机渐近性行为，以期待得到一些不同于相应的确定性系统的结果。

文中令(Ω，F，{Ft}t≥0，P)表示带有{Ft}t≥0且满足通常条件(即单调增加且右连续的且F0包含所有的P零空集)的全概率空间。

1 系统(3)的正解存在唯一性

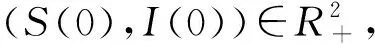
证明 对t≥0,考虑系统

(4)

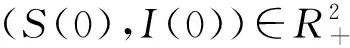
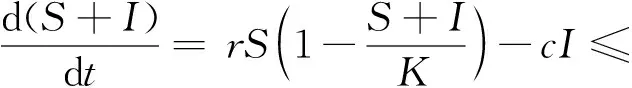
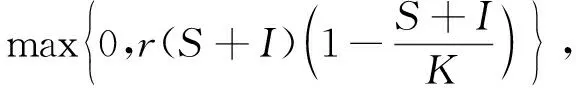
(5)

则

S(t)+I(t)≤

K。

(6)

现在,我们将证明这个解是几乎必然全局的,就等价于证明τe=∞几乎必然成立。选择足够大的k0≥0,使得S(0),I(0)全部位于区间[1/k0,k0]内。对每一个整数k≥k0,定义

τk=inf{t∈[0,τe):min{S(t),I(t)}≤

1/kor max{S(t),I(t)}≥k}。

(7)

P{τk≤T}≥εfor allk≥k1,

(8)

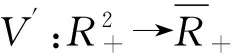
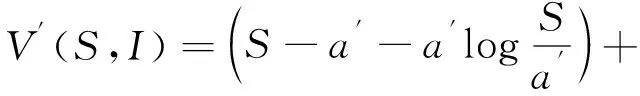
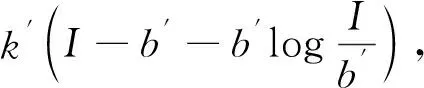
(9)

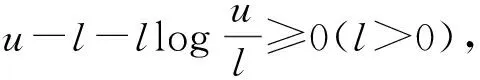
k′(I-b′)[(βS-c)dt+σSdB(t)]+

LV′dt+σ[-(S-a′)I+k′(I-b′)S]dB(t),

(10)

其中

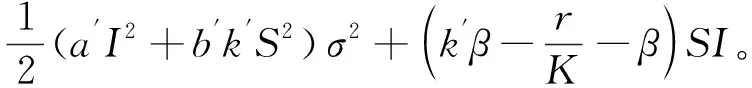
(11)

首先,选取

满足

其次,选取

和

满足

和

则

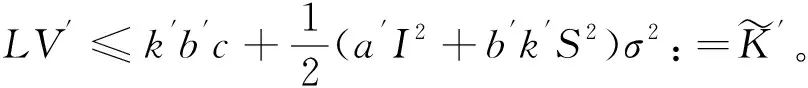
(12)

因此

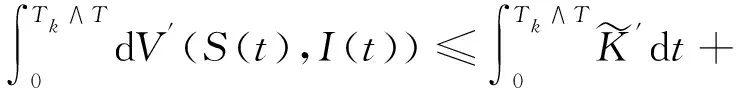
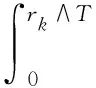
(13)

则推得,

E[V′(S(τk∧T),I(τk∧T))]≤V′(S(0),I(0))+

(14)

当k≥k1时,令Ωk={τk≤T}且由式(8)有,P(Ωk)≥ε。注意到对每一个ω∈Ωk,在S(τk,ω),I(τk,ω)中至少有一个达到k或1/k,因此

h′(k),

(15)

其中h′(k)是k的函数,且

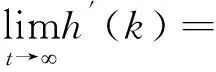
再由式(8)和式(14)有

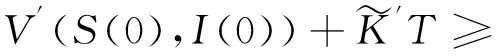
E[1Ωk(ω)V′(S(Tk∧T),I(Tk∧T))]≥

εh′(k),

(16)

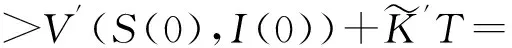
注1从定理可以得到

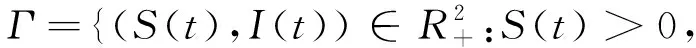
I(t)>0,S(t)+I(t)≤K},

(17)

是系统(3)的正不变集。从现在开始，我们总是假设初始值(S(0),I(0))∈Γ。

2 系统(3)的灭绝性和持久性

定理2今(S(t),I(t))为系统(3)满足初始条件(S(0),I(0))∈Γ的解。假设:

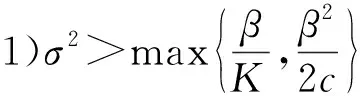
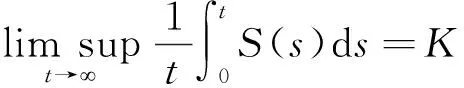
证明 由Itǒ's公式,有

(18)

令

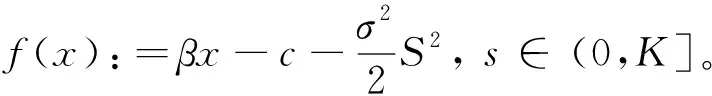
(19)

下面分两种情形讨论。

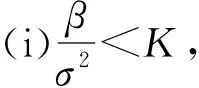
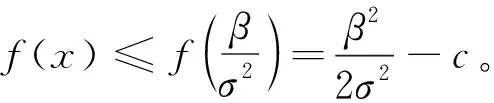
(20)

则有

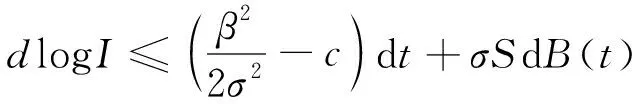
(21)

和

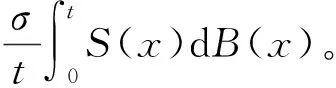
(22)

令

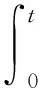
它是一个实值连续局部鞅,M(0)=0且有

K2<∞a.s.

(23)

再由强大数定律,证得

(24)

几乎必然成立。再由式(22)得到

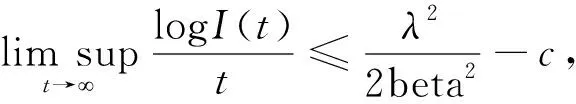
(25)

几乎必然成立。由条件1)非常容易得到

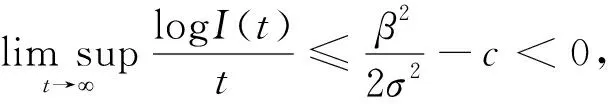
(26)

几乎必然成立。也就是说,I(t)几乎必然以指数收敛于0。换句话说,已感染者依概率1死亡。

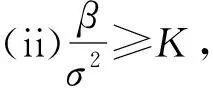
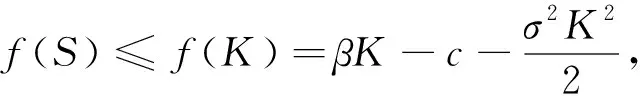
(27)

则

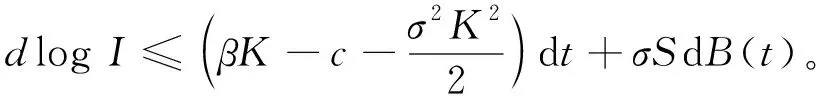
(28)

类似于(i)中的讨论,得到

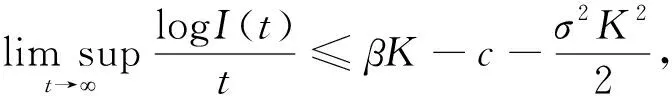
(29)

几乎必然成立,使用条件2),可得到

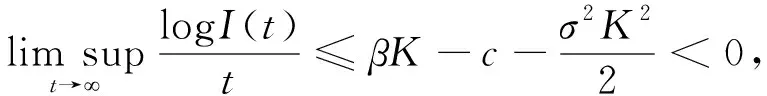
(30)

几乎必然成立。即I(t)以指数几乎必然趋于0。换句话说,已感染者依概率1死亡。

再由Itǒ's公式,有

σIdB(t),

(31)

则有

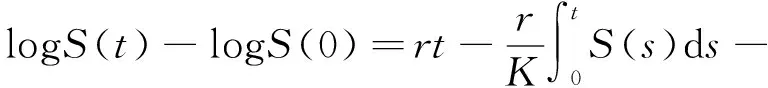
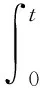
(32)

和

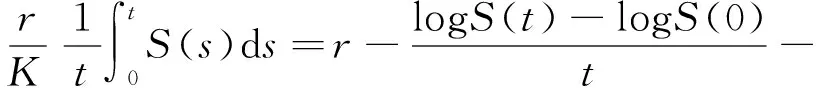
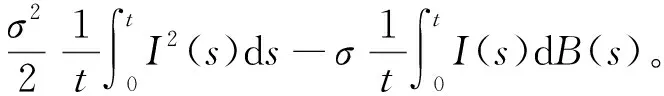
(33)

再由上式,可得

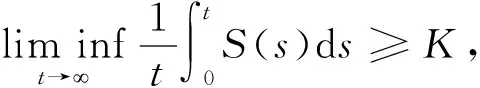
(34)

几乎必然成立。由于

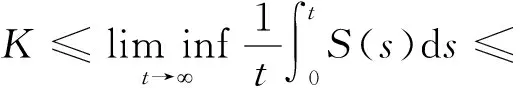
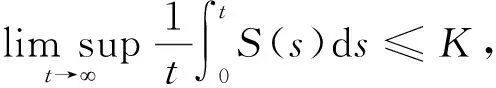
(35)

几乎必然成立。

我们得到

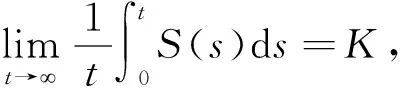
(36)

几乎必然成立。