基于IPSO-SVR模型的弯管部冲蚀率预测

于海跃， 刘浩楠

(长春工业大学 机电工程学院， 吉林 长春 130012)

0 引 言

在工业管道正常进行运输中,不可避免地会在其中掺杂固体颗粒，从而发生固体颗粒的冲蚀，会对管道内壁尤其是管道弯头处产生较大的冲蚀磨损，当腐蚀和冲蚀发生耦合时,其冲蚀率会进一步加大，而管道内壁因固体颗粒对管道内壁的冲蚀作用会导致内壁变薄，由此造成的应力聚集是事故发生的主要原因，而准确地预测管道的冲蚀率能够为管道的剩余使用寿命预测以及维修策略的制定提供强有力的支持。董争亮等[1]采用CFD数值模拟方法对90°弯管内壁的冲蚀问题进行研究，使用最小二乘法进行非线性拟合，并且得到了多种因素对弯管冲蚀的影响规律。胡瑾秋等[2]以正交实验为基础,得出各因素对冲蚀磨损结果的影响排序，得到了弯头形态与流速是工程设计时首先考虑的因素。孙晓阳等[3]引入蒙特卡罗方法(DSMC)结合CFD数值模拟对管道进行冲蚀预测，通过5种不同的冲蚀模型对比发现，在保证预测精度的前提下,可节省大量算力。黎伟等[4]通过CFD-DPM模型求解弯管在流体作用下固体颗粒的冲蚀问题，并得到冲蚀位置主要在弯管出口的水平两侧,以及弯管入口的垂直两侧。Zahedi P等[5]使用相关的实验参数作为预测变量，利用机器学习算法中的随机森林算法来预测侵蚀率，并在不同条件下用测试数据验证预测结果。Zhu H J等[6]研究受侵蚀弯管中的温度分布，并找到一种新的方法来预测侵蚀削减管壁的厚度。Yu W C等[7]对90°标准弯头中的壁面侵蚀进行了CFD研究，采用基于Euler-Euler方法的颗粒湍流动能模型进行侵蚀预测，其结果与实验结果较为吻合。

综上所述，目前使用数值模拟的方法针对弯管冲蚀率的研究较多，对特定情况下的预测准确率高，且可解释性强，但是对先验知识的要求也较高，文中将以数据角度为基础，以机器学习与智能优化算法为手段，为管道弯头部冲蚀磨损的预测提供新思路。

1 SVR算法

SVR是由统计学习理论为基础衍生出来的监督学习算法，该算法的适应性强，在二维平面或者多维空间中仍有不错的表现，能够较有效地避免过拟合的出现，同时也能在小样本数据中取得较好的效果，SVR与支持向量分类在使用过程中原理大致相同。SVR 的主要优点之一是无论输入特征维度的大小，其计算的繁杂程度不会被影响;另一方面，在具有较高泛化能力的同时，也能进行精确预测。

SVR通过计算求解得到最优超平面，建立以

f(x)=wTx+b

为中心，2ε为宽度的间隔带,使得各个数据点与超平面的距离都小于ε,

f(x)=wTφ(x)+b,

(1)

式中：φ(x)----非线性函数，其作用是将x映射到高维空间，与f(x)构成线性关系;

w，b----分别为权重和偏置;

f(xi)----输出的预测值。

SVR的优化问题为

(2)

s.t.yi-wTxi-b≤ε,

wTxi+b-yi≤ε,

式中：yi----实际值。

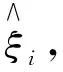
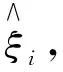
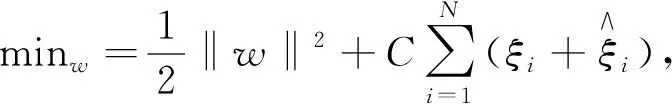
(3)

s.t.yi-wTxi-b≤ε+ξi,

式中:C----损失权重的常数。

进一步将拉格朗日乘子与核函数[8]引入 SVR,

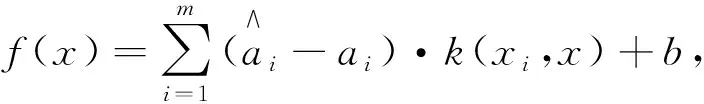
(4)

式中：m----样本数量;

k(xi，x)----核函数。

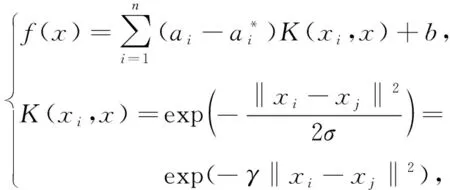
(5)

式中:σ----核函数的宽度。

SVR模型精度主要取决于其中的损失权重常数C和高斯核函数中的参数γ。损失权重常数C过小时，对间隔带以外的样本数据惩罚较小，训练误差较大，在预测冲蚀磨损时的误差也较大，如果损失权重常数C过大时，对间隔带以外的样本数据惩罚较大，模型精度随之提升，但其泛化性会降低，往往导致模型过拟合的出现；核函数的参数γ则是影响了支持向量之间的聚合程度，γ越小，支持向量之间关系越不紧密，因此,在拟合过程中模型会变得特别复杂，泛化能力就会降低；γ越大，则支持向量之间就会越紧密，冲蚀预测模型难以达到预期的精度，因此，引入IPSO智能优化算法的根本目的则是找到最合适的C与γ。

2 IPSO优化算法

粒子群优化算法(PSO)是Kennedy J等[9]和Eberhart R等[10]提出的基于群体智能的全局随机搜索的智能优化算法，该算法在工程领域以及其他领域中被广泛使用，以解决各种优化问题。算法初始化会生成随机粒子，通过不断迭代寻找全局最优解，每次迭代过程会产生当代种群中的个体极值pbesti，个体极值与全局极值gbest进行对比，通过两个极值相比，从而进行不断更新。其原理如下。

假设在一个D维的目标搜索空间中，有N个粒子组成一个群落，其中第i个粒子表示一个D维的向量，

Xi=(xi1，xi2，xi3，…，xiD)，i=1，2，…，N。

粒子i的第d维速度更新为

(6)

粒子i的第d维位置更新为

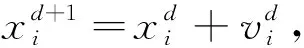
(7)

式中：c1----个体学习因子，c1越大，粒子越倾向于以往个体所达到的极值;

c2----社会学习因子，c2越大，粒子越倾向于全局极值;

vi----粒子i的速度向量;

r1,r2----[0，1]上的随机数;

w----惯性权重系数,w越大，其搜索范围越大。

传统PSO算法在寻优过程中会存在容易陷入局部最优和收敛速度较慢等问题，其算法的效率较难保证，因此，文中引入粒子自适应权重系数，使得粒子惯性权重能随着算法迭代代数增加而发生改变，从而使得算法在迭代初期能够获得更大的搜索范围，避免陷入局部最优，而在算法迭代后期能够缩小搜索范围，不易错过全局最优解。自适应惯性权重系数为

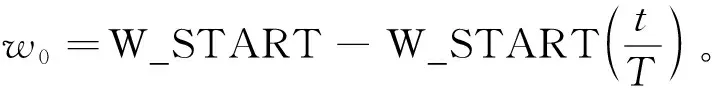
(8)

改进粒子群算法步骤如下：

1)初始化粒子群，并设定最大迭代次数T，当前迭代次数为t。

2)计算各个粒子的适应度值。

3)计算每个粒子的适应度值与其迭代的最佳位置pbesti的适应度值相比，若较好，则更新为当前的个体最佳位置。

4)计算每个粒子的适应度值与全局最佳位置gbest的适应度值相比，若较好，则更新为全局最优位置。

5)引入自适应权重w0，根据速度、位置公式对粒子的速度和位置进行优化，从而更新粒子位置。

6)如未达到最大循环数T，则返回2)继续进行计算。

3 IPSO-SVR模型构建

在数学最优化问题中，Rosenbrock 函数是一个用来测试最优化算法性能的非凸函数，由Howard Harry Rosenbrock在1960年提出Rosenbrock函数的定义为

f(x，y)=(1-x)2+100(y-x2)2。

(9)

Rosenbrock函数的每个等高线大致呈抛物线形，其全局最小值也位于抛物线形的凹形区域中。由于凹形区域中的值变化较小，要找到全局最小值较为困难。其全局最小值位于 (x,y)=(1，1)点，数值为f(x,y)=0。第二项的系数不同，但不会影响全局最小值。其函数图象如图1所示。

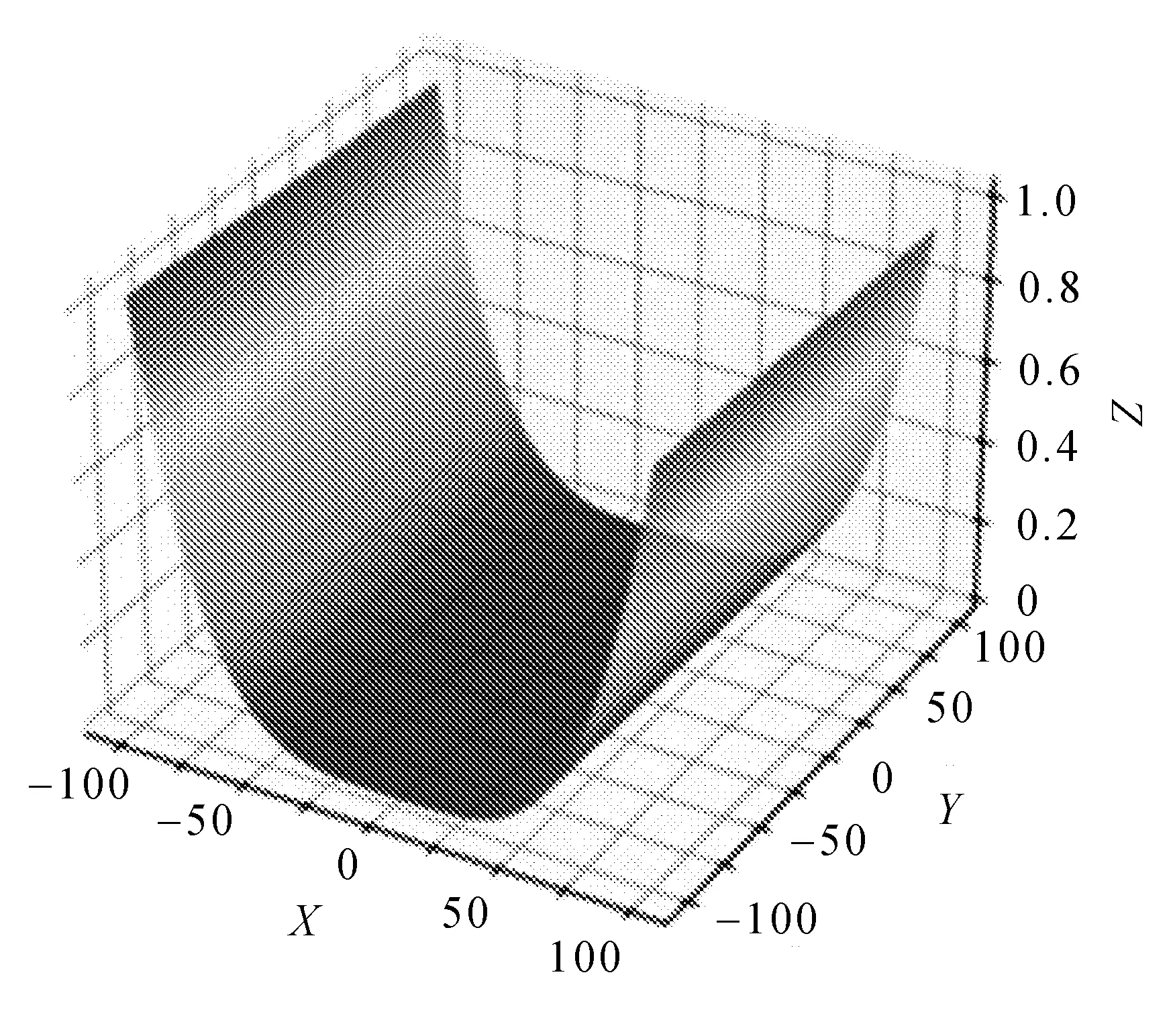
图1 Rosenbrock函数图象

使用传统PSO算法与IPSO算法进行对比，实验结果见表1。

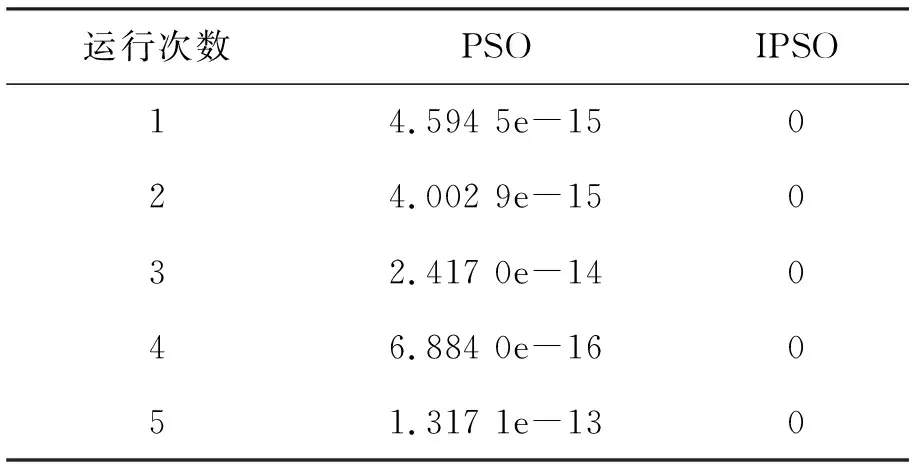
表1 PSO、IPSO算法对Rosenbrock函数求解全局最小值结果比对

传统PSO算法虽然能够寻得局部极小值，但是对于全局最小值的搜索依然较为困难，而IPSO算法能够保证每一次都能寻找到全局最小值。

PSO和IPSO适应度迭代过程适应度进化曲线分别如图2和图3所示。

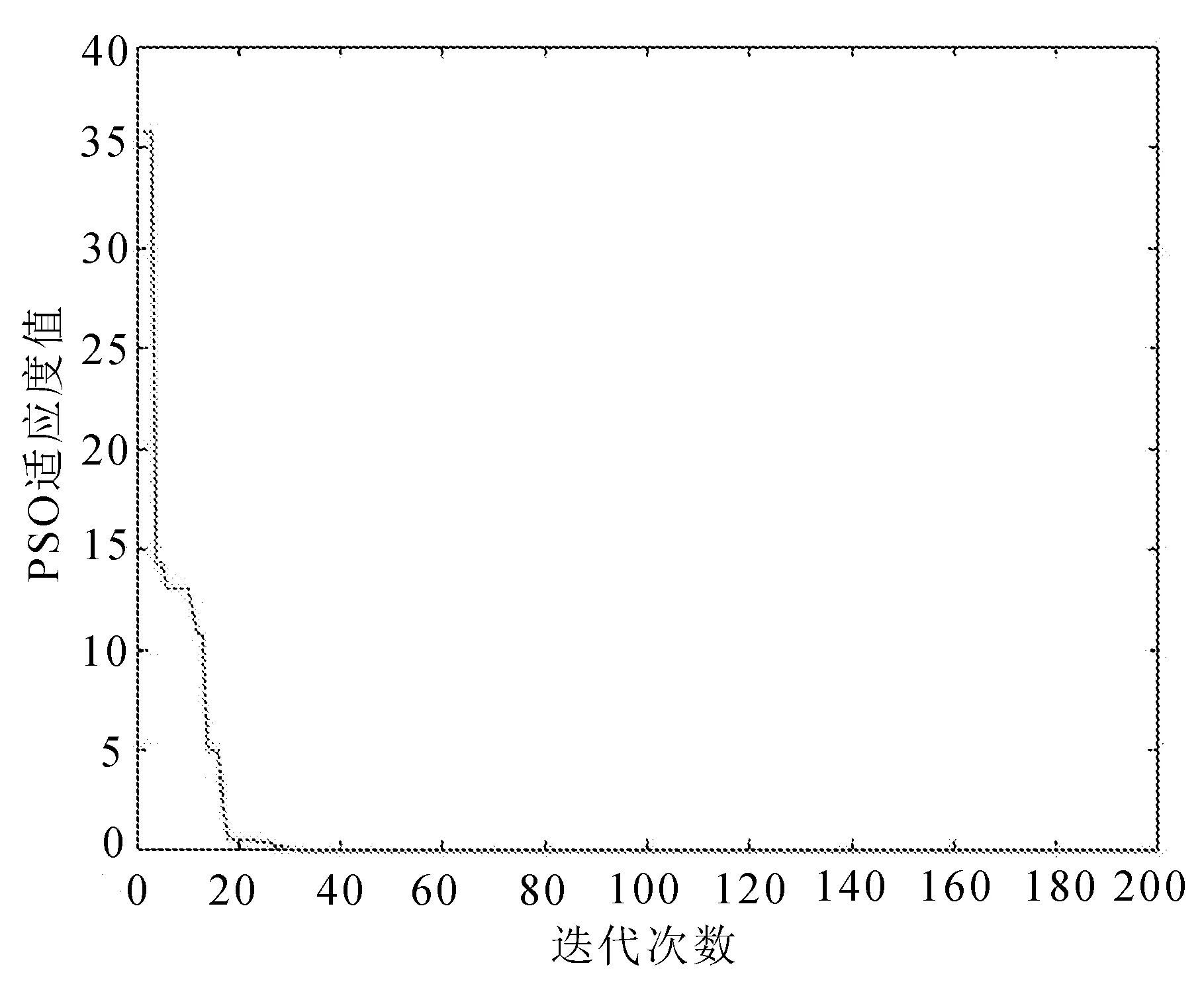
图2 PSO适应度迭代过程适应度进化曲线

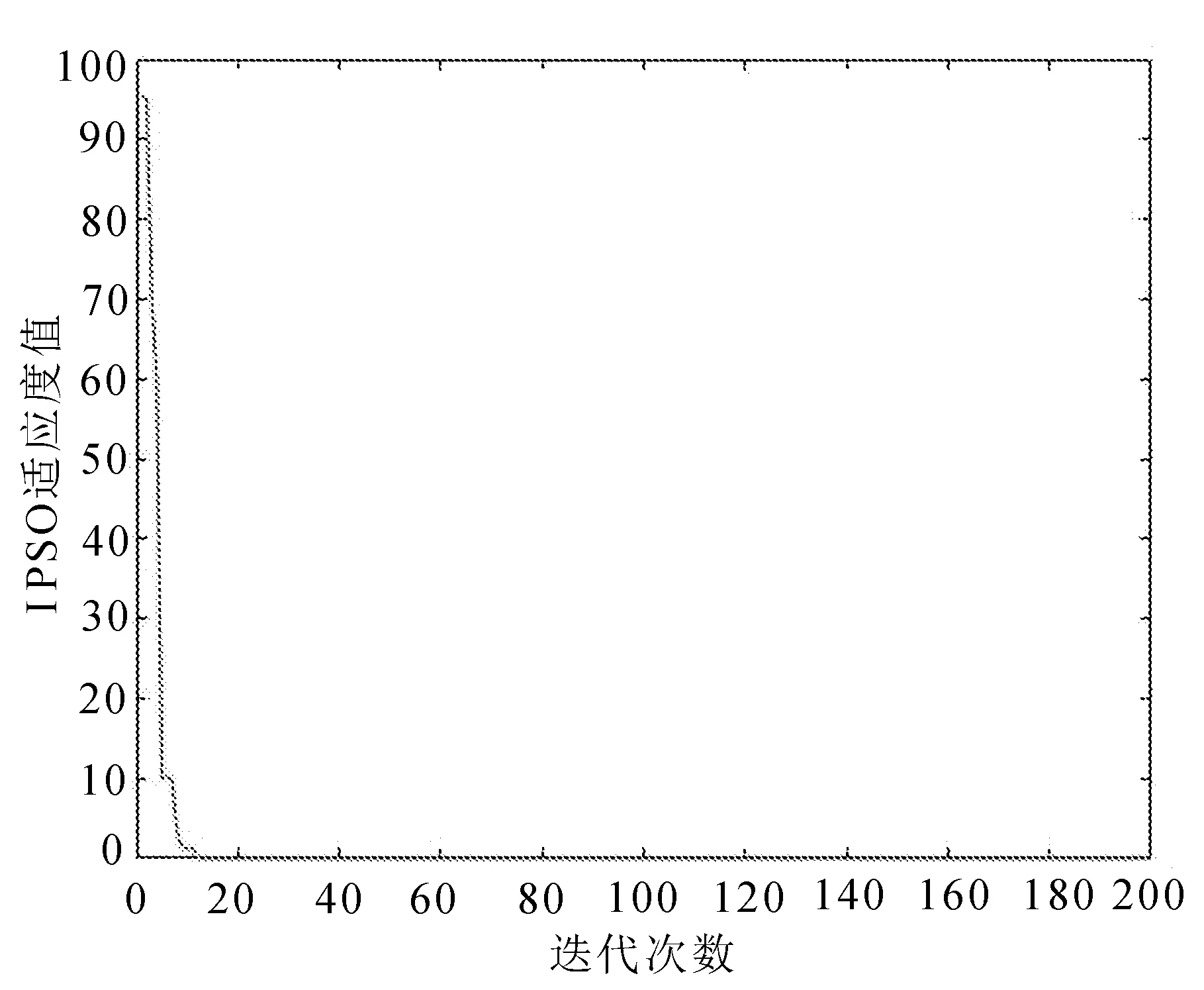
图3 IPSO适应度迭代过程适应度进化曲线

图3相较于图2，传统PSO算法在30代左右开始收敛，IPSO算法在10代左右已经开始收敛，这是由于自适应惯性权重的引入使得算法能够避免陷入局部最优，提升了寻优能力以及收敛速度。

实验具体参数设置为：群体粒子个数N=100；粒子维数D=2；最大迭代次数T=200；学习因子c1=1.5，c2=1.5；PSO惯性权重W=0.7；IPSO初始惯性权重W_START=0.9，分别使用PSO与IPSO进行全局最小值的搜索。

由以上结果可以得出，IPSO在寻优能力以及算法的收敛速度方面都优于原本的PSO。

IPSO-SVR模型步骤如图4所示。

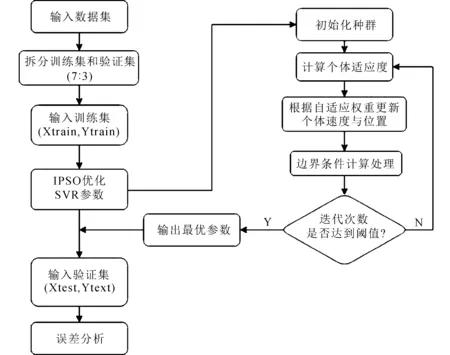
图4 IPSO-SVR模型流程

4 IPSO-SVR模型预测弯管部冲蚀率

文中选择201个较为广泛的实验数据点组成的数据集[5]，数据集1(源自Vieira (2014)，Parsi (2015)，Pyboyina (2006)，Muzamder (2004)，Salama (1998)-AEA Data)中包含6个特征，分别为管道材料、管道直径、粒子尺寸、流体黏度、流体表面速度、气体表面速度。

数据集2(源自Bourgoyne (1989)，Kesana (2013)，Vieira (2014)，Salama (1998)-AEA Data)中包含4个特征，分别是管道材料、管道直径、粒子尺寸、气体表层速度。数据集的数据分布见表2。

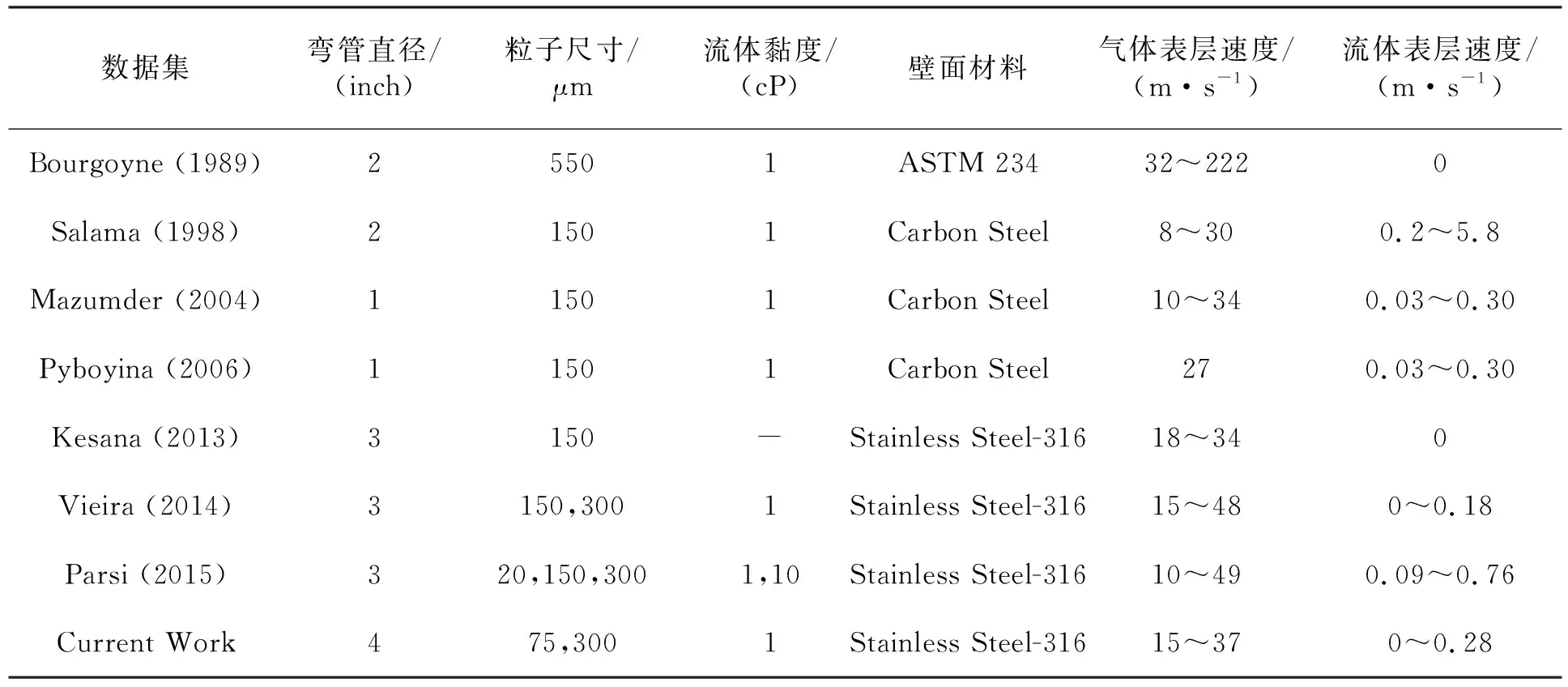
表2 冲蚀数据参数分布

文中将用三个指标对SVR模型与IPSO-SVR模型进行比较，分别为决定系数(R2)、平均绝对误差(Mean Absolute Error， MAE)、均方误差(Mean Square Error， MSE)，其定义分别为：

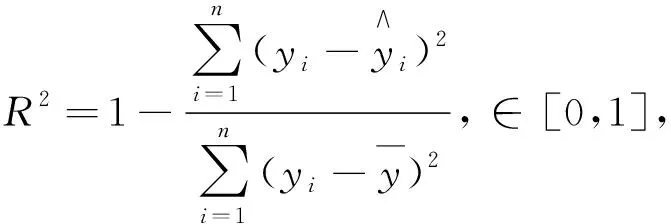
(10)

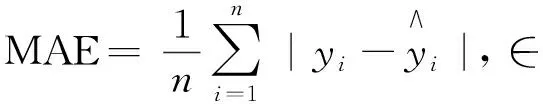
(11)

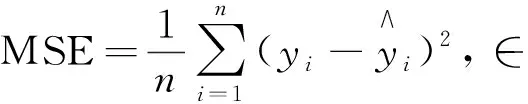
(12)

式中：n----预测样本的数量;

yi----实际实验中的冲蚀磨损值;

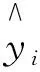
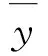
采用SVR与IPSO-SVR两种算法对弯管冲蚀率预测结果分别如图5～图8所示。

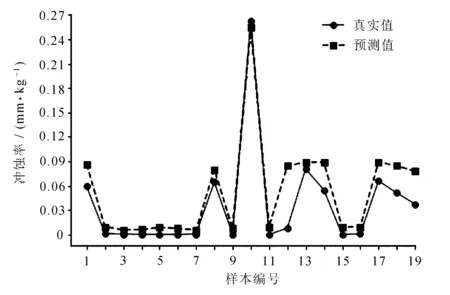
图5 SVR预测数据集1结果图

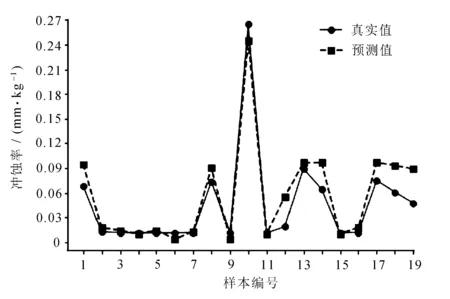
图6 IPSO-SVR预测数据集1结果图

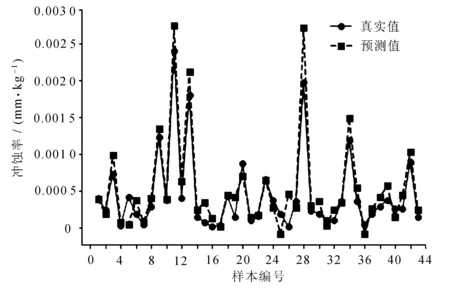
图7 SVR预测数据集2结果图

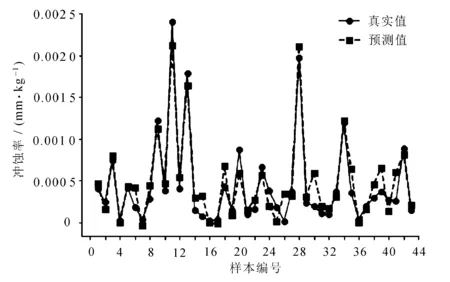
图8 IPSO-SVR预测数据集2结果图

使用IPSO-SVR模型分别对数据集1与数据集2的R2最高可达0.900 5与0.888 2，相较于SVR模型分别提升约6%与5.5%；MAE分别降低0.038 1与0.017 2；MSE分别降低0.031 7与0.009 4。经过IPSO优化后的SVR模型可以更为拟合地预测弯管部的冲蚀率，其误差在减小，R2在提高。

数据集1和数据集2算法的评价指标对比分别见表3和表4。

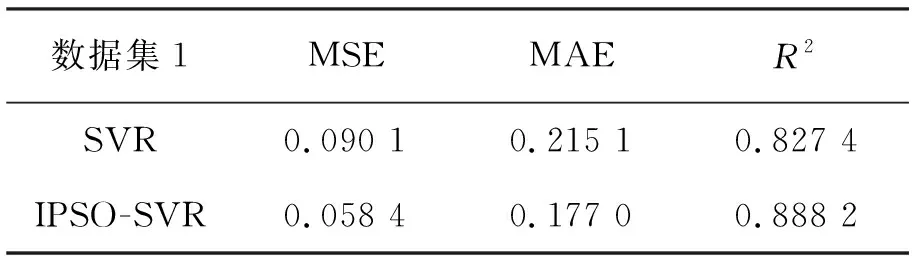
表3 数据集1中算法的评价指标对比

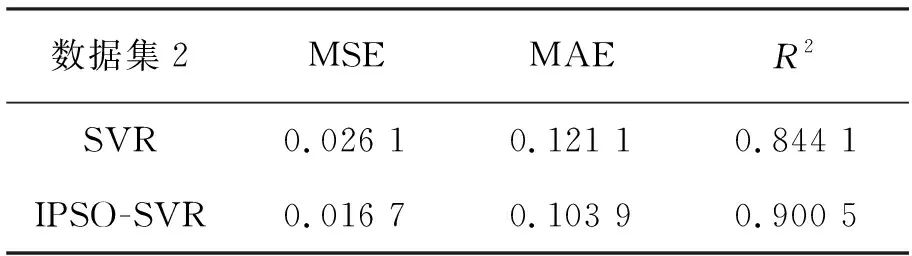
表4 数据集2中算法的评价指标对比

5 结 语

首先对粒子群算法进行了改进，并使用Rosenbrock函数对粒子群算法以及改进粒子群算法的性能进行比对，之后使用改进粒子群算法对支持向量回归模型进行优化，最后使用两个数据集对模型进行训练，并对管道弯头处的冲蚀率进行预测。通过结果可得到以下结论：

1)与传统粒子群算法相比，改进后的粒子群算法具有更好的全局搜索能力，能提高大约2倍的收敛速度。

2)使用改进后的粒子群算法对支持向量回归算法进行优化后得到IPSO-SVR模型，相较于一般的支持向量回归，IPSO-SVR算法的预测精度最高可达90.05%，且误差也更小，能够更为准确地预测管道弯头部位的冲蚀率。