总体极小向后扰动块方法求解多右端对称线性方程组
朱景福,李欣,孟亚辉
(广东石油化工学院理学院,茂名 525000)
在理论研究和工程应用中,比如控制理论、工程振动反问题、结构力学等许多领域的应用中经常遇到求解多右端对称项线性方程组

其中A∊Rn×n是非奇异对称矩阵,X,B∊Rn×S。
块krylov子空间方法[1]是求解多右端线性方程组的常用方法。块方法的基本思想是,在求解多右端线性方程组时,不是对每一个方程都单独应用迭代法的方式,而是采用同时对所有方程应用迭代,这样的计算方法会更有效。块方法一经产生就引起了数学家们的很大兴趣。在上世纪八十年代Underwood.R和Saad Y[2-3]就提出了块lanczos方法。1980年O’Leary在共轭梯度法(CG)的基础上提出了的块CG方法(BCG)[4],九十年代初Sadkan.M和Vital.B提出求解对称正定方程组的块Davidson方法[5],进一步论证了块方法的有效性。1996年Simoncini V和Gallopoulos E[6-7]提出了块GMRES方法(BGMRES)及其变形。1997年Freund R W和Malhotra M[8]提出求解多右端的非Hermitian线性方程组的块QMR方法(BQMR),同年Chan T F和Wan W L[9]对求解多右端线性方程组的投影方法做了较全面的分析。1999年顾桂定等提出了求解多右端非对称线性方程组的块EN方法(BEN)[10-11]。2000年戴华[12]教授研究了求解多右边大型稀疏对称线性方程组的块Lanczos算法和块Minres算法,并建立了两种算法之间的关系。2008年钟宝江等[13]提出了一种更简单的块GMRES方法,该方法避免了块上Hessenberg矩阵的因式分解。因此,编程要简单得多,所需的工作也少得多。同年张建华等[14]提出求解具有多个右端项线性方程组的总体CGS算法。Taherian A和Toutounian F[15]提出了求解多右端非对称线性方程组的块GPBi-CG方法。一般地,在讨论算法的收敛性和稳定性时,Krylov子空间方法通常用残量范数作为判断算法终止的条件,即极小残量法[16-18]。通常,若近似解是精确的,残量范数是小的,但是反过来不一定。为克服残量范数作为终止条件的不足,数学工作者们考虑采用系数矩阵扰动的方法求解线性方程组,1995-1997年Kasenally[19-20]在用GMRES方法解非对称线性方程组时,考虑求满足扰动方程的近似解使向后扰动范数‖△A‖F极小化,给出了求解大型非对称线性方程组的广义极小向后扰动方法。1998年曹志浩[22]推广了广义极小向后扰动方法,把总体向后扰动方程的精确解看做所求方程的精确解,给出求解大型非对称线性方程组的总体GMBACK方法[21]。孙继广在2001年出版了《矩阵扰动分析》,系统地研究了矩阵特征值扰动分析和求解方程组的扰动分析问题。李欣等[23-24]提出了求解对称线性方程组的总体最小扰动方法和求解对称多右端位移方程组的种子投影方法。Zhang Lei-Hong等[25]提出向后摄动分析和基于残差的误差界的线性相关特征值问题。
考虑在求解多右端对称线性方程组时,采用块Lanczos过程与总体极小向后扰动相结合的方法,分析论证总体向后扰动的格式及总体极小向后扰动范数的求法,建立求解多右端对称线性方程组的总体极小向后扰动块方法。本文的结构安排如下:首先引言和预备知识;在求解多右端对称线性方程组的块Lanczos过程中,做总体向后扰动分析,提出用总体极小向后扰动范数作为判断算法终止的准则,给出总体极小向后扰动块lanczos方法;最后通过数值实验验证新算法的可行性和有效性。
1 预备知识
下面先引入一些所采用的记号、基本概念和引理。
A+表示矩阵A的Moore-Penrose广义逆。
‖A‖F、‖A‖2分别表示矩阵A的Frobenius范数和2-范数。
xT和XT分别表示向量x和矩阵X的转置。
νec(A)表示矩阵A的列拉直(列展开)。
A⊗B表示A与B的Kronecker积(直积,张量积)。
上面定义的记号均见参考文献[26]。
引理2.1[26]设A∈Cm×n,B∈Cn×p,C∈Cp×q,则νec(ABC)=(CT⊗A)νec(B)。
引理2.2设A∈Cm×n,则‖A‖F=‖νec(A)‖2。
证明由矩阵的Frobenius范数定义和2-范数定义结合矩阵的列拉直定义易得。
引理2.3[26]设A∈Cm×n,B∈Cp×q,C∈Cm×q,矩阵方程AXB=C有解的充分必要条件为AA+CB+B=C,在有解的情况下AXB=C的通解为

其中Y∈Cn×p是任意的,A+为矩阵A的Moore-Penrose广义逆;如果AXB=C无解,则AXB=C的最小二乘解仍为(2.1),并且AXB=C的极小最小二乘解为X=A+CB+。
引理2.4[26]设A是任意的m×n矩阵,若A的奇异值分解为

其中U∈Rm×m和V∈Rn×n,Σ=diag(σ1,σ2,…σr)(σ1,σ2,…σr是A的正奇异值),则的Moore-Penrose广义逆A+

证明由Moore-Penrose广义逆的定义直接验证可得。
下面回顾块Lanczos过程。首先选取多右端项对称线性方程组AX=B(1.1)的初始矩阵X0,并由QR分解得到X0=Q1T1。
算法2.1块Lanczos过程[2-3,26]
(1)选取(1.1)的初始矩阵X0,X0=Q1T1;令Q0=0,计算M1=Q1TAQ1;
(2)for j=1:k
(2.1)计算Pj+1=AQj-Qj-1TTj-QjMj;
(2.2)将Pj+1进行QR分解Pj+1=Qj+1Tj+1,其中Qj+1是n×s规范正交矩阵,Tj+1是s×s的上三角矩阵;
(2.3)计算Mj+1=QTj+1AQj+1;
End for


上式两边同时左乘以分块矩阵(Q1Q2…Qk),
因为Qk是规范正交矩阵,则有
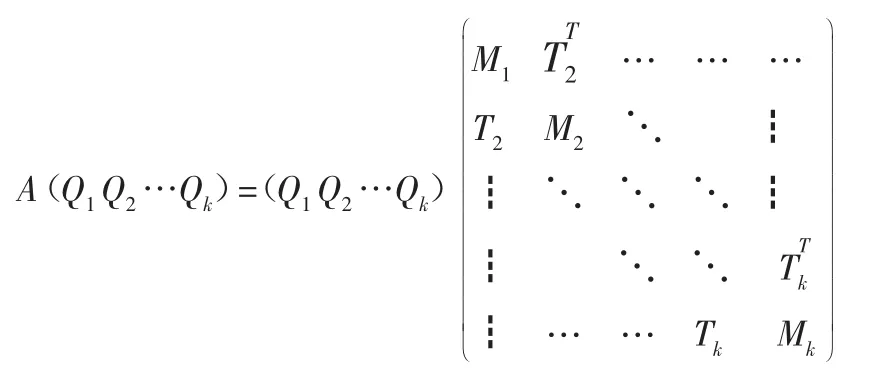
由矩阵的分块乘法易得
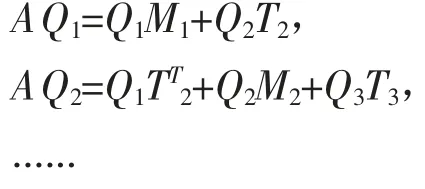
用通式表示为三项递推公式

变形为
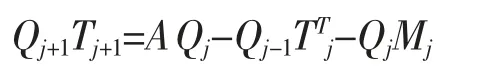
若记Qj+1Tj+1=Pj+1,即对Pj+1做QR分解可得Qj+1和Tj+1,再计算Mj+1=QTj+1AQj+1,即可得Mj+1,这样可构造出矩阵及。
在(2.2)式中的三项递推公式可用如下矩阵形式来表示

则(2.3)式可以表示为

设x0(i)(i=1,…,s)是有s个右端项的对称线性方程组(1.1)的初始估计,记X0=[x0(1),x0(2),…,x0(s)],则R0=B-AX0=[r0(1),…,r0(s)]。
可令根据块Lanczos方法产生的方程组(1.1)的近似解有如下形式:
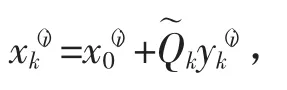
用矩阵表示为

其中Yk=[yk(1),yk(2),…,yk(s)],由Yk=EkR1求出相应的Yk。残量矩阵表示为

2 总体极小向后扰动块方法
2.1 总体极小向后扰动分析
本节讨论如何建立求解多右端对称线性方程组(1.1)总体极小向后扰动的块方法,如何构造总体向后扰动的格式,以及总体极小向后扰动范数的求法,在新方法执行块Lanczos的过程中如何与总体极小向后扰动相结合。
首先把多右端对称线性方程组AX=B(1.1)的近似解看作扰动方程

的精确解。这里我们把[△,δ]称为总体向后扰动。这种求解方程组(1.1)近似解的方法,称作扰动方法,多年来扰动方法得到广大数学工作者的重视,见参考文献[19,20,21,23]。
下面讨论把块Lanczos过程与总体极小向后扰动方法相结合求解(2.6)式中的Yk,即求解满足min{‖△,δ‖F|(A-△)X=B+δ}的Yk值。
首先以定理的形式给出总体向后扰动的格式,以及总体极小向后扰动范数的求法。
定理3.1若Xk∈Rn×S是方程组(3.1)的精确解,则总体向后扰动[△,δ]=-Rk(XkTXk+E)-1(XkTE),且总体极小向后扰动范数为
这里νec(*)表示矩阵*的列拉直。‖*‖F表示矩阵*的Frobenius范数,‖*‖2表示矩阵*的2范数。具体定义见参考文献[26]。
证明:设Xk∈Rn×S是(3.1)的精确解,代入扰动方程(3.1),则

若记Rk=B-AXk表示方程组(1.1)的残量,则上式可化为

由矩阵乘法,上面的(3.2)式可以看作

由引理2.3方法解此矩阵方程,得总体向后扰动

下面考虑求解总体向后扰动[△,δ]的范数的极小值,由引理2.4得

由Frobenius范数和2-范数的定义及引理2.1和引理2.2

化简为

则
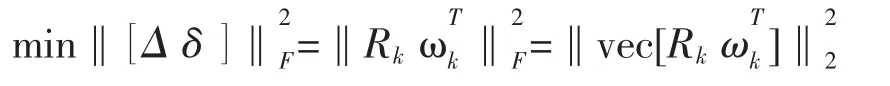
即

证毕。
2.2 总体极小向后扰动块方法
根据3.1节的分析,本文在求解方程组(1.1)的块Lanczos过程中,把(3.5)式的总体极小向后扰动范数作为迭代终止的条件,在满足一定精度要求时,给出求解多右端对称线性方程组的如下算法——总体极小向后扰动块Lanczos方法(TBMINBACK)。
算法3.1总体极小向后扰动块Lanczos方法(TBMINBACK)

3 数值实验
数值实验均在个人计算机上实现,具体配置:CPU:intel(R)Core(TM)i7-8550u,主频:1.8GHz,内存:8GB,系统:Win10企业版,软件:Matlab R2014a
由于Matlab软件的优越性,在算法的执行过程中,比如QR分解、求矩阵的范数等,都可以直接调用现成的命令得到,这对算法的执行带来了更便利的条件。
下面利用算法2.1块Lanczos方法(记为BLanczos)和算法3.1(TBMINBACK)两种方法求解方程组(1.1),把两种方法的计算速度和残量做对比,比较两种方法的有效性。
例4.1已知对称矩阵


表1 两种方法残量对比Table 1 Residual comparison of two methods
由表1可见,在求解多右端对称方程组(1.1)时,TBMINBACK方法和BLanczos方法的计算速度都达到小数点后的第三位,但两者差距很小,这是因为TBMINBACK方法是在BLanczos的基础上改进的,两者都采用了块Lanczos过程,新方法的运算步骤相对增加,自然运算速度会有相应的增加。但是,在目前计算机性能日新月异的改进中,如此小的速度差异可以忽略不计。更重要的是,显然TBMINBACK方法计算的残量范数更小。
例4.2已知对称矩阵

解:选取方程组(1.1)的初始估计X0=当矩阵A的规模n=100,块Lanczos过程循环次数k=8时,随着右端项B的列数S变化,用算法2.1(BLanczos)和算法3.1(TBMINBACK)两种方法求解方程组(1.1),实验结果见表2。

表2 两种方法残量对比Table 2 Residual comparison of two methods
由表2进一步得出TBMINBACK方法的残量范数比BLanczos方法的更小。特别是,当多右端项的列数S比较大时,TBMINBACK方法的残量更加小。说明新方法对于多右端项更大型的对称线性方程组的求解更有效。
4 结论
提出了求解多右端对称线性方程组的新方法——总体极小向后扰动块Lanczos方法(TBMINBACK)。新算法在块Lanczos方法的基础上做了改进,把总体极小向后扰动范数作为迭代的终止条件,建立了总体极小向后扰动块Lanczos方法(TBMINBACK),论文给出了总体向后扰动的格式和总体极小向后扰动范数的求法,并对新算法做了残量分析,从理论证明了新方法的可行性。
数值实验结果表明总体极小向后扰动块Lanczos方法(TBMINBACK)在求解方程组(1.1)时,残量范数达到小数点后10位且明显优于块Lanczos方法(BLanczos)。数值实验进一步验证了新方法的可行性、有效性和优越性。特别是,当多右端项的列数S比较大时,TBMINBACK方法的残量更加小。说明新方法对于多右端项更大型的对称线性方程组的求解更有效。
需要说明的是在数值实验环节,本文选取的多右端对称线性方程组(1.1)的系数矩阵A都是比较大型的,同时也考虑了系数矩阵A的非零元素比例的情况(稠密或者稀疏)。通过多组实验发现,在系数矩阵A比较稀疏的情况下,总体极小向后扰动块Lanczos方法(TBMINBACK)更有优势。稀疏矩阵方程组的求解问题,在大型科学工程计算、图像处理等研究领域经常会遇到,说明新算法具有一定的实践意义。

