雾计算中支持计算外包的微型属性加密方案*

王 峥,孙 枭

(太原理工大学信息与计算机学院，山西 晋中 030600)

1 引言

云计算作为一种网络资源，被广泛应用于人们的日常生活中。然而随着物联网技术的快速发展，数据爆发式地增长，海量数据被存储到云服务器上。传统的云计算模式面临计算过于集中、系统效率低下等问题[1]。2012年，思科提出了雾计算的概念，将网络计算从云计算中心扩展到了网络边缘，为物联网提供了更加高效的服务[2]。然而数据存储在云端或雾节点中，在为人们提供便利的同时，也带来了数据的安全性问题[3，4]。为了保护数据的隐私，在上传数据之前，需将其进行加密。密文策略属性加密CP-ABE(Ciphertext-Policy Attribute-Based Encryption)[5]将解密规则嵌入到加密算法中，不仅保证了数据的安全性，而且还实现了一对多灵活的访问控制，被认为是云存储系统中的首选安全方案。

近年来，移动设备更加普及(如智能手机、笔记本电脑等)，然而大多数CP-ABE方案[6-10]中密钥与密文的长度随属性数量线性增长，较大的存储开销无疑限制了该方案在资源有限的物联网设备上的实际应用。因此，学者们在方案的轻量化改进方面进行了许多工作。Emura等人[11]提出了第1个密文定长的方案;Guo等人[12]实现了密钥定长；Odelu等人[13]同时实现了密钥与密文定长。但是,上述方案中的访问策略仅支持(n,n)门限，难以实现灵活的策略表达。Herranz等人[14]提出了一种密文定长的方案，且支持(t,n)门限访问，但加密阶段需要n+t+1次指数运算，解密阶段需要O(t2)次指数运算。为了解决效率低下的问题，Chen等人[15]提出了一种固定计算开销的方案;唐忠原等人[16]提出了一种密钥与密文都定长的方案，引入RSA算法的思想，简化了加解密计算，但方案的安全性相对较低。

现有的CP-ABE方案大多是基于双线性映射实现的，然而加解密过程中配对操作的次数与访问策略中的属性数量呈线性正相关。因此，对于移动终端而言，较长的加解密时间极大地影响了用户体验。计算外包是一种降低客户端计算负担的有效方法，在传统云存储中，Green等人[17]首次提出了解密外包的新范式;Li等人[18]与王树兰等人[19]都提出了可验证的外包解密方案，且分别固定了密文与密钥的长度，但均未实现加密外包；Ma等人[20]将复杂的加解密计算分别外包给加解密服务提供商，客户端只需进行一次模幂运算，但同时增加了通信开销与安全风险。随着雾计算技术的逐渐成熟，雾节点层被加入到基于云存储的物联网系统，云雾架构随之形成。Zuo等人[21]提出了一种适用于雾计算的外包解密方案，且具有选择密文攻击下的不可区分性IND-CCA(INDistinguishability under Chosen-Ciphertext Attack)安全。Zhang等人[22]将与访问策略相关的加密计算与部分解密计算外包给雾节点，但存储开销较大的问题并未得到改善。

基于上述问题，本文在雾环境中构建了一个支持计算外包的微型CP-ABE方案。该方案不仅可以使密钥与密文长度恒定，而且还支持(t,n)门限访问，策略表达能力更强。此外，该方案还支持可验证的加解密计算外包，减少了客户端的加解密时间，系统效率更高，适用于资源有限的移动设备。

2 相关知识

2.1 双线性映射

设G1,G2和GT是阶为素数p的乘法循环群，g和h分别是G1和G2的生成元。若映射e:G1×G2→GT为一个双线性映射，则它满足如下性质：

双线性：对任意a,b∈Zp，e(ga,hb)=e(g,h)ab成立。

非退化性：e(g,h)≠1。

可计算性：存在一个有效的算法能够计算出e(g,h)。

2.2 aMSE-DDH难题

构造双线性配对群G={G1,G2,GT,p,e}，假设f(x)和g(x)为群Zρ[x]上互质的多项式，g0和h0分别是G1和G2的生成元,α和γ是群Zp上的随机数。给定下述参数:

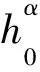
aMSE-DDH难题就是判断S是GT上的随机数或者S=e(g0,h0)γf(α)。若对任意τ多项式时间攻击者，解决此难题的最大优势为ε，那么称它为(τ,ε)困难问题。

2.3 访问树

访问树是以树状图的方式表达访问控制策略，树中存在2种节点：一种是叶子节点,代表属性，另一种是非叶子节点,代表关系函数。只有属性集合满足策略的用户才能够成功解密密文。

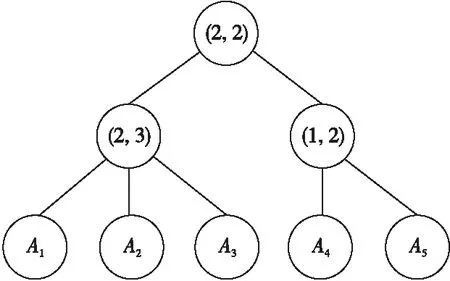
Figure 1 Access tree

2.4 安全模型

本文所提方案的安全模型通过挑战者B与攻击者A交互进行的攻击游戏来定义：

(1)初始化阶段：A提交挑战访问结构T*给B。

(2)系统建立阶段：B输入安全参数1k，生成公共参数PK和主密钥MSK，并将PK发送给A。

(3)查询阶段1：A能够向B发起如下查询：

①任意属性集合Ai的密钥。

②密文Encrypt[Ti,Mi]的解密。

(4)挑战阶段：如果A没有查询过属性集A(T*⊆A)的密钥，那么A将消息M0和M1发送给B。B随机选择c′∈{0,1}，然后利用T*将消息Mc′加密，生成挑战密文Encrypt[T*,Mc′]发送给A。

(5)查询阶段2：A重复对密钥和密文查询，但是有如下要求：

①不能查询属性集A(T*⊆A)的密钥。

②不能查询密文Encrypt[T*,Mc′]的解密。

(6)猜测阶段：A提出猜测c′g∈{0,1}。如果c′g=c′，那么A取胜。

上述游戏中，A的优势ε=Pr[c′g=c′]-1/2。

定义1若任意τ多项式时间的A在进行至多qs次密钥查询和qd次解密查询后，ε对于1k可忽略，则该方案具有(τ,qs,qd,ε)selective-IND-CCA安全。

3 系统描述与方案构造

3.1 系统描述

本文所提方案的系统模型如图2所示，包括5个不同的实体：可信授权机构TA(Trusted Authority)、云服务器CS(Cloud Server)、雾节点FN(Fog Node)、数据拥有者DO(Data Owner)和数据用户DU(Data User)。

Figure 2 System model

(1)可信授权机构：TA被其他实体完全信任，所有属性都由它管理。TA负责系统建立，为整个系统生成公共参数PK和主密钥MSK，并分别为FN和DU生成雾节点密钥FKA和用户密钥UKA。

(2)云服务器：CS拥有巨大的存储空间和丰富的计算资源，但它并不是完全可信的。CS接收DO加密的数据后代为存储，并为DU提供下载数据的服务。

(3)雾节点：FN是一些性能相对较弱、地理位置分散的各种功能计算机，也不是完全可信的。每个FN都与CS相连，在加密阶段，FN首先接收DO上传的访问策略P,并生成部分加密密文CT′返回给DO,当DO进行完全加密生成密文CT之后，将CT上传至CS存储。在解密阶段，FN下载CT并进行预解密生成部分解密密文M′，然后发送给DU。

(4)数据拥有者：DO是希望将数据上传至CS存储的一方，本文主要是指资源有限的移动设备。DO利用访问树制定访问策略将数据加密成密文，进而实现一对多的访问控制。

(5)数据用户：DU是希望访问存储在CS中数据的一方，也是指资源有限的移动设备。只有自身属性满足访问策略的DU才能够解密密文获得数据。

3.2 方案构造

本文所提方案的总体框架如图3所示，包含4个阶段，分别是系统建立阶段、密钥生成阶段、数据加密阶段和数据解密阶段。所有阶段都由多项式时间的算法来实现，下面对各个阶段的算法实现进行详细说明。算法中各变量的含义说明如表1所示。

共包含以下6个算法：

算法1Setup(1k,U)→(PK,MSK)/*该算法由TA执行*/

Table 1 Variable definition

Figure 3 Total framework of the proposed scheme

输入：系统安全参数1k和全局属性集合U。

输出：公共参数PK和主密钥MSK。//PK是公开的，MSK由TA保存

Step1构造双线性群BG=(G1,G2,GT,p,e)，并计算e(g,h)。

Step2随机选取α,r,s∈Zp，并计算gα，hi=hαi，ui=hαir，vi=hαis,i=1,2,…,n。

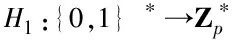
Step4生成主密钥MSK={g,α,r,s}和公共参数PK={BG,e(g,h),gα,hi,ui,vi,H1,H2}。

算法2KeyGen(PK,MSK,A)→(FKA,UKA)//该算法由TA执行

输入：公共参数PK、主密钥MSK和用户属性集合A。

输出：雾节点密钥FKA和用户密钥UKA。

Step2选取2个随机数k1,σ∈Zp，计算可得k2=(1/f(α,A)-k1s)/r。

Step3生成雾节点密钥FKA={gk1/σ,gk2/σ}和用户密钥UKA=σ。

算法3Encrypt.Fog(PK,T)→CT′/*该算法由FN执行*/

输入：公共参数PK和访问树T。

输出：部分加密密文CT′。

Step1设T由m个子树构成，将T转换为T1=b11b12…b1n,…,Tm=bm1bm2…bmn。

Step3计算U′1=hrf(α,T1,…,U′m=hrf(α,Tm)和V′1=hsf(α,T1,…,V′m=hsf(α,Tm)。

Step4生成部分密文CT′，然后FN将其发送给DO。

算法4Encrypt.DO(PK,M,CT′)→CT//该算法由DO执行

输入：公共参数PK，待加密的明文消息M和部分密文CT′。

输出：密文CT。

Step1随机选取β∈Zp，并计算以下参数:R,U1,…,Um,V1,…,Vm,C1,C2。

R=(gα)β=gαβ,

U1=U′β1=hrf(α,T1)β,…,Um=U′βm=hrf(α,Tm)β，

V1=V′β1=hsf(α,T1)β,…,Vm=V′βm=hsf(α,Tm)β，

C1=e(g,h)β·M，C2=H2(e(g,h)β)⊕M

Step2生成密文CT，CT={T1,…,Tm,U1,…,Um,V1,…,Vm,R,C1,C2},并将其发送至CS。

算法5Decrypt.Fog(PK,CT,FKA)→M′//该算法由FN执行

输入:公共参数PK、密文CT和雾节点密钥FKA。

输出:部分解密密文M′或⊥。

Step1若用户属性集合A与访问树T中的子树都不匹配就直接中止，输出⊥；否则计算A与T中所有子树间的汉明距离d1,…,dm，并选取最小汉明距离dmin对应的子树继续后续步骤。

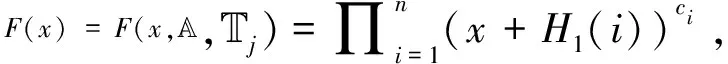
Step3计算X,Y,Z,W的值:

X=e(gk2/σ,Uj)=e(g,h)rf(α,Tj)βk2/σ,

Y=e(gk1/σ,Vj)=e(g,h)sf(α,Tj)βk1/σ,

W=X·Y=e(g,h)βF(α)/σ

Step4生成部分解密密文M′，M′={F0,Z,W,C1,C2},然后FN将其发送给DU。

算法6Decrypt.DU(PK,M′,UKA)→M//该算法由DU执行

输入：公共参数PK、部分解密密文M′和用户密钥UKA。

输出：明文M或⊥。

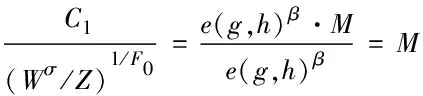
4 安全性证明

在上述安全模型中，基于aMSE-DDH难题，采用反证法对本文所提方案的安全性进行证明。

假设存在一个攻击者A能以(τ,qs,qd,ε)的优势攻破本文方案安全性，则可以构造一个算法B以至少(τ′,ε′)的优势解决aMSE-DDH难题。A与B之间的交互如下所示：

(1)初始化：A将树T*发送给B，假设T*=Tj=bj1bj2…bjn。

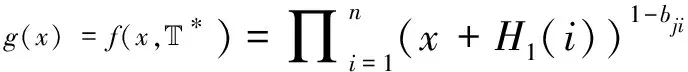
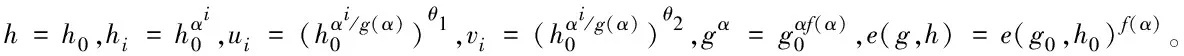
A可以查询随机模型H1和H2的值。B通过列表LH1和LH2分别存储对H1和H2的查询与返回的结果。若本次查询已有先前的回应且输出结果记录在列表中，则B返回该结果。当面临新的查询时，B采取如下措施：

①查询H1(i)的值。T*=bj1bj2…bjn，当bji=0时，B选择g(x)的一个新根值返回给A；当bji=1时，B选择f(x)的一个新根值返回给A(i∈[1,n])。

②查询H2(ti)的值，B随机选择Qi∈{0,1}lM返回给A。

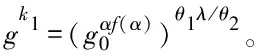
对于解密结果Encrypt[Ti,Mi]→CTi的查询。若本次查询出现在查询列表中，B输出相应的结果Mi，否则输出⊥。

(4)挑战：如果所有被查询的密钥都不能满足T*，则A输出挑战消息(M0,M1)。B随机选取b∈{0,1}，使用T*对消息Mb进行加密，生成挑战密文CT*的步骤如下所示：

(5)查询阶段2：A重复查询阶段1的操作。限制条件是：

①没有密钥查询满足挑战的访问结构。

②对于挑战的密文没有解密查询。

(6)猜测：A输出一个猜测b′∈{0,1}。若A已经查询过H2(S)的值，B输出1;否则B输出0，S是GT上的一个随机数。

在猜测阶段，若A能以优势ε获胜，则S=e(g,h)β至少以ε+1/2优势存在于LH2中。只要S不存在LH2中,S就仅是一个随机数，因此，S至多以qH2/p优势存在于LH2中，故B能够以至少ε-qH2/p的优势分辨S是GT上的一个随机数或者S=e(g0,h0)γf(α)。因此,本方案具有selective-IND-CCA安全。

5 性能评估

5.1 理论分析

5.1.1 功能比较

相关方案的功能比较如表2所示。

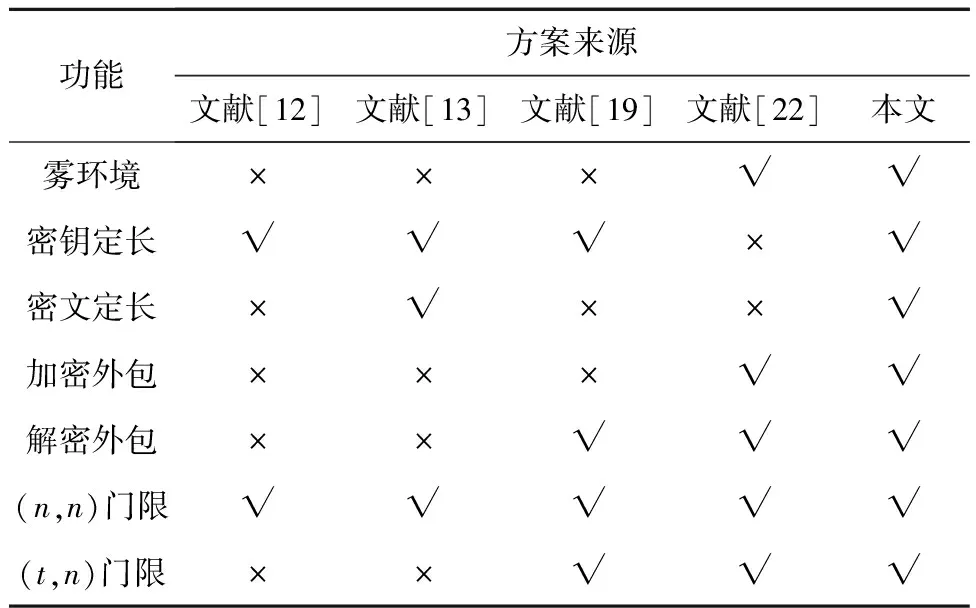
Table 2 Comparison of function

文献[12]方案实现了密钥定长，但密文长度并未固定，仍随着属性数量成倍增长，在具有海量用户的应用场景中，会带来巨大的密文存储负担，且该方案无任何计算外包能力，策略表达能力也相对较弱。文献[13]方案与文献[12]方案相比，实现了密文定长，但仍仅支持(n,n)门限访问，策略表达相对单一，难以构造灵活的访问策略，且在计算效率方面也无任何提升。文献[19]方案在文献[12]方案的基础上，增强了策略表达能力，使方案能够实现“与”门、“或”门和“门限”3种访问策略，并将部分解密计算外包给云服务器。但是，鉴于云服务器现存的计算过于集中等问题，在处理大量外包计算任务时，系统效率相对较低，且该方案并不支持加密外包，也没有固定密文的长度。

上述方案均不适用于雾计算环境，文献[22]方案实现了雾环境中的加解密计算外包且支持(t,n)门限访问，但密钥与密文长度不能固定，随着属性数量的增加，造成了较大的存储负担。而本文所提方案实现了雾环境中的加解密部分外包，具有定长的密钥与密文，且支持较为灵活的策略表达。

5.1.2 存储成本比较

相关方案的存储成本比较如表3所示。

Table 3 Comparison of storage cost

对于密钥而言，文献[22]方案中用户密钥的长度与用户的属性数量呈线性正相关，并不适用于资源有限的物联网设备。文献[12,13,19]方案与本文方案实现了密钥长度恒定，但本文方案的密钥存储成本最小，仅为一个群元素的大小。

对于密文而言，文献[12,19]方案密文长度与全局属性数量呈线性正相关。文献[22]方案密文长度随访问策略中的属性数量线性增长。文献[13]方案与本文方案中密文长度与属性数量无关，但文献[13]方案仅支持(n,n)门限访问。当m=1时，本文方案与文献[13]方案中的访问策略相同，即仅支持(n,n)门限访问。而当m≠1时，本文方案支持(t,n)门限访问，如果文献[13]方案想要实现与本文方案相同的策略表达，那么文献[13]方案需要进行m次加密操作，密文长度等于3m|G|,大于本文方案。为了便于理解，此处举例进行说明：假设制定如图1的访问策略，该策略可以转换为6个仅支持“与”门的访问策略。此时文献[13]方案需要进行6次加密运算，密文存储成本为3|G|·6=18|G|，而本文方案的密文存储成本为(2·6+1)|G|=13|G|。因此，本文方案在密文存储成本方面也优于其他方案。

5.1.3 计算复杂度比较

相关方案中客户端在加解密时的计算复杂度比较如表4所示。

Table 4 Comparison of computational complexity

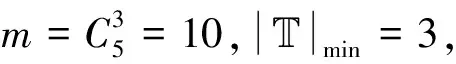
通过上述对相关方案的比较与分析可以发现，本文方案的存储成本与计算开销均独立于属性数量，综合性能更优，适用于资源有限的物联网设备。

5.2 实验分析

为了验证方案的有效性，本文通过实验仿真将相关方案的客户端加解密时间进行比较。以Java Paring-Based Cryptography library为基础，选取超奇异曲线y2=x3+x在512-bit有限域上的160-bit椭圆曲线群，实现了相同的访问控制策略，达到了80-bit安全级别。由于客户端的智能移动设备种类较多，本节对相关方案在笔记本电脑和智能手机2种设备上的性能表现进行评估。电脑的实验环境采用Windows 10操作系统，Eclipse IDE，Intel Core i7-4720HQ处理器，12 GB RAM；手机的实验环境采用Android 10操作系统，Android IDE，Kirin 980处理器，8 GB RAM。所有实验数据均为50次模拟取平均值，实验结果如图4～图7所示。

在图4和图5中，随着系统设置的属性数量增加，文献[12,13,19]方案数据拥有者加密所消耗的时间都线性增加，而文献[22]方案与本文方案中的时间开销都几乎为一个定值。在本文方案中数据拥有者只需完成2m+1次指数运算、1次乘法运算和1次异或运算，这些计算均与属性数量无关，加密过程中与访问策略相关的大量复杂计算都已经转载到了雾节点，数据拥有者只需要完成剩余的少量计算即可，大幅度降低了数据拥有者的计算开销。

Figure 4 Time of personal computer encryption

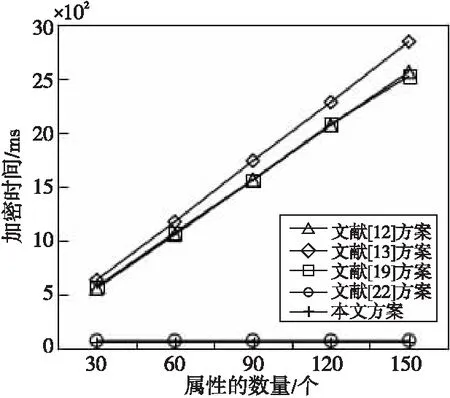
Figure 5 Time of mobile phone encryption

在图6和图7中，文献[12,13]方案的用户解密时间均与系统设置的属性数量呈线性正相关。而本文方案与文献[19,22]方案实现了解密外包服务，时间开销几乎保持不变，但本文方案与文献[19]方案在电脑和手机上的解密效率最高。这是因为解密过程中多项式函数的生成与复杂的双线性配对等操作都已经外包给了雾节点，用户只需进行2次指数运算、3次除法运算和1次异或运算，即可解密并完成验证，大大减轻了用户的计算负担。当属性数量增长到150个时，文献[13]方案在手机上的解密时间接近1.5 s，而本文方案仍为10 ms左右，因此本文方案适用于具有海量用户的应用场景。

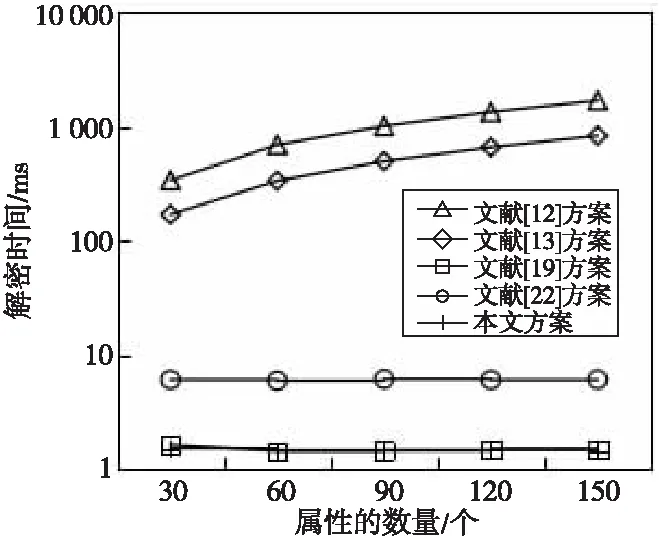
Figure 6 Time of personal computer decryption

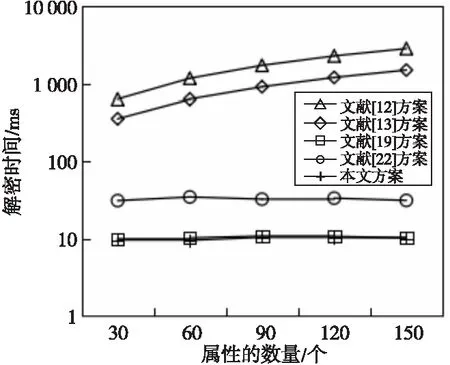
Figure 7 Time of mobile phone decryption

6 结束语

本文针对目前属性加密方案中客户端存储与计算成本较高的问题，基于雾计算平台提出了一种支持计算外包的微型访问控制方案。首先，本文方案中密钥与密文定长，加解密计算外包，减轻了终端设备的开销。其次，数据拥有者定制了个性化的访问策略，本文方案能够为用户提供高效的数据共享。再次，用户通过简单的哈希与异或运算就能够检验外包解密结果正确与否。最后，经证明本文方案具有selective-IND-CCA安全，即使雾节点与云服务器不可信，也能够保障数据的隐私安全。但是，目前本文方案并未考虑到用户与属性撤销的问题，而用户与属性通常是多对多的关系，复杂度较高，如何构造一个高效的撤销机制是接下来应研究的问题。