代价约束算法对入侵检测特征提取的优化研究*
刘 云,郑文凤,张 轶
(昆明理工大学信息工程与自动化学院,云南 昆明 650500)
1 引言
恶意网络攻击带来了严重的安全问题,入侵检测系统IDS(Intrusion Detection System)对维护网络安全尤为重要[1]。数据特征提取则是IDS防御的关键,选择相关不冗余的数据特征可以提高模型的检测准确性[2,3]。针对类不平衡的高维数据特征,深度学习方法可以直接从原始数据中自动提取相关特征,快速处理高维复杂数据[4]。因此,利用深度学习模型可降低传统特征提取算法的计算复杂度,应对复杂数据集的特征提取,提高IDS的识别精度[5]。
Yang等人[6]结合稀疏自编码器SAE(Sparse AutoEncoder)和降噪自编码器DAE(Denoising AutoEncoder)的优点,设计了融合自编码器FAE(Fusion AutoEncoder)深度学习算法,提出了多级降噪和重采样的方法解决数据丢失和不平衡问题,FAE增强了模型的适用性和数据特征提取的学习能力,比传统自动编码器AE(AutoEncoder)具有更精确的检测效果。Shone等人[7]根据深度学习和浅层学习的模型,提出非对称深度自动编码器NDAE(Nonsymmetric Deep AutoEncoder)学习算法,使用堆叠的NDAE和随机森林构建深度学习分类模型,可有效进行无监督的特征学习,降低了非对称数据维数并显著减少模型的训练时间,算法准确性与普通深度神经网络算法相比更优。
为了从高维复杂数据中自动提取重要特征,构建更加可靠的IDS,本文提出代价约束算法CCA(Cost Constraint Algorithm),并将其集成到AE中进行无监督的特征学习。首先构建深度学习的神经网络模型,利用L2正则化和稀疏约束方法优化目标函数;然后根据类别样本分布生成的代价矩阵调整神经网络模型的参数,通过堆叠多层的自编码器学习数据特征;最终在分类器中输入提取的约简特征检测分类结果。仿真结果表明,CCA减少了特征的冗余度,且对少数攻击类别数据的识别更敏感,相比其他现有算法检测网络异常数据的精度更高。
2 基于深度学习的入侵检测模型
2.1 入侵检测模型
入侵检测模型通过入侵检测识别网络攻击行为,并给出适当的警告以提高网络的安全性,该模型主要由数据特征提取和分类组成,其中,基于深度学习方法进行特征提取可以快速降低数据维度,并获得更有效的数据特征[8]。为了应对大规模入侵数据,研究人员通常选择多层神经元构成的自编码器构建新的入侵检测模型,其结构如图1所示。

Figure 1 Intrusion detection model based on autoencoder
在图1中,模型先用AE自动提取一组数据向量x=(x1,x2,…,xn)的相关特征,其中,xi表示第i个(i∈{1,2,…,n})训练数据向量,n是输入数据的总数。将最后一个隐藏层输出的重构数据和特征作为分类层的输入,优化损失函数得到模型的分类结果。Softmax是自编码器常用的分类器,适用于解决多分类问题,可用该分类器作为检测算法的输出层。Softmax函数将多个神经元的输出映射到[0,1],计算每个样本数据分类为某个类别的概率如式(1)所示[9]。
(1)
其中,j∈{0,1,2,…,c}表示数据的类别;yi表示数据xi的类标记,如yi=0时,式(1)表示数据预测为正常网络流量的概率。θ为训练时的参数向量,θj为数据属于第j类的参数。因此,入侵检测模型通过P(yi=j|xi;θ)评估数据类别的概率值,为了进一步反向调节神经网络参数,一般通过最小化交叉熵损失函数来实现,计算公式如式(2)所示:
(2)
其中,N表示训练样本的个数,I{yi=j}表示标签yi属于类别j的可能性,如果yi=j,则I=1,否则I为0。
由AE构成的入侵检测模型,可以实现高维数据空间到低维数据空间的非线性转换,但这种神经网络只能学习简单的数据特征。为了快速发现复杂数据中的重要信息,提取更深层次的数据特征,需要在基本的神经网络上进行优化。通常的做法是在神经网络的隐藏层添加约束或者重复多次学习,提高入侵检测模型的检测精度和收敛性[10]。
2.2 栈式稀疏自编码器
将多个AE堆叠在一起学习的方法称为栈式自编码器SAE(Stacked AutoEncoder)[10]。为了降低时间复杂度,本文使用堆叠2个隐藏层的自编码神经网络进行深度学习,将最终提取的数据特征输入分类器,其结构如图2所示。
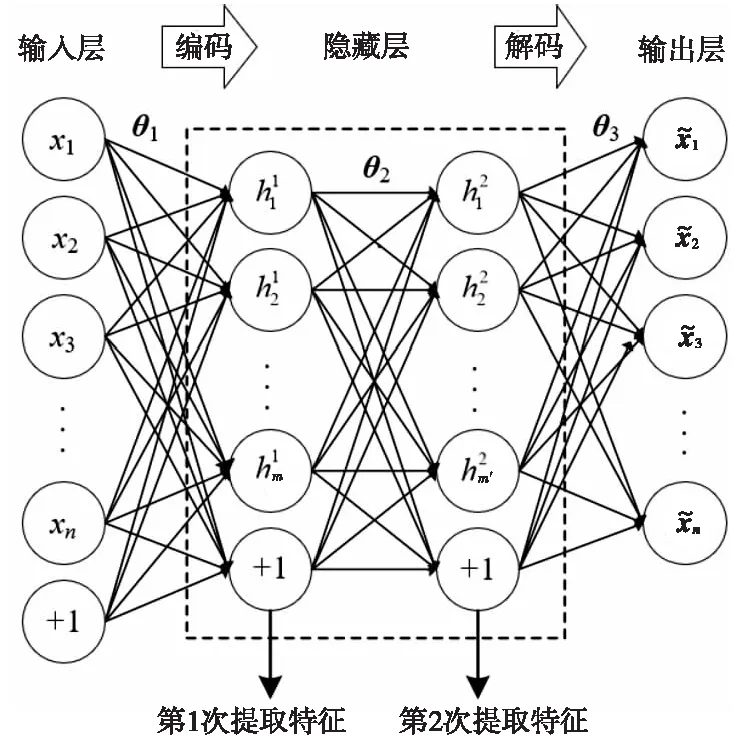
Figure 2 Structure of stacked autoencoder
输入层、隐藏层和输出层是SAE深度学习的基本组成,m和m′分别是隐藏层神经元的数量,+1是偏向神经元。神经网络的上一层的输出用作自编码器的下一层的输入,以便获得输入数据更高级别的特征表示。
无监督的神经网络深度特征提取模型,学习数据的特征表示主要包含2个学习过程:编码和解码,编码过程如式(3)所示[11]:
h=f(Wx+b)
(3)
其中,f(·)表示编码器的非线性激活函数,W∈Rm×n表示编码权重矩阵,b∈Rm表示编码偏置向量。
式(3)将输入向量x映射到隐藏层,编码结果用h表示,然后用解码激活函数g(·)重构隐藏表示h,如式(4)所示:
(4)
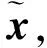
(5)
通过最小化重构误差,可优化特征提取参数。
隐藏层的输出数据是原始数据的低维表示,对隐藏神经元施加稀疏约束,选择性地激活相关的神经元,构成栈式稀疏自编码器SSAE(Stacked Sparse AutoEncoder)[3]。第k个神经元的平均激活如式(6)所示:
(6)
其中,ak(xi)表示在输入xi时隐藏神经元k的激活度。

(7)


(8)
在稀疏惩罚项中,β为稀疏控制权重系数,其值在0~1。
常见的特征提取算法主要基于类别分布平衡的数据,但在实际入侵检测中,数据存在严重的类不平衡问题,不同类别的攻击存在明显的分布不均。数据分布不均会严重影响算法的性能,为了提高IDS的可靠性,所提算法在特征提取中引入代价敏感学习方法,可获得更加有效的低维数据特征[14]。
3 代价约束算法(CCA)
3.1 代价矩阵
为了降低IDS的误报率,正确识别未知攻击数据的入侵行为,需要增强少样本数据特征的敏感性。用采样技术平衡训练数据的传统方法具有一定的局限性,因此,将根据不同类别的样本分布提出的代价矩阵C,集成到SSAE中进行特征学习,可提取稀缺数据的相关特征,提高IDS的可靠性。
表1表示具有5个类别数据集的代价矩阵C,其中,Cij表示实际类别i被预测为类别j的代价。当i=j时,Cij=0,表示正确分类的代价;当i≠j时,Cij> 0,表示错误分类的代价,数据分类错误的代价根据式(9)的样本分布计算。
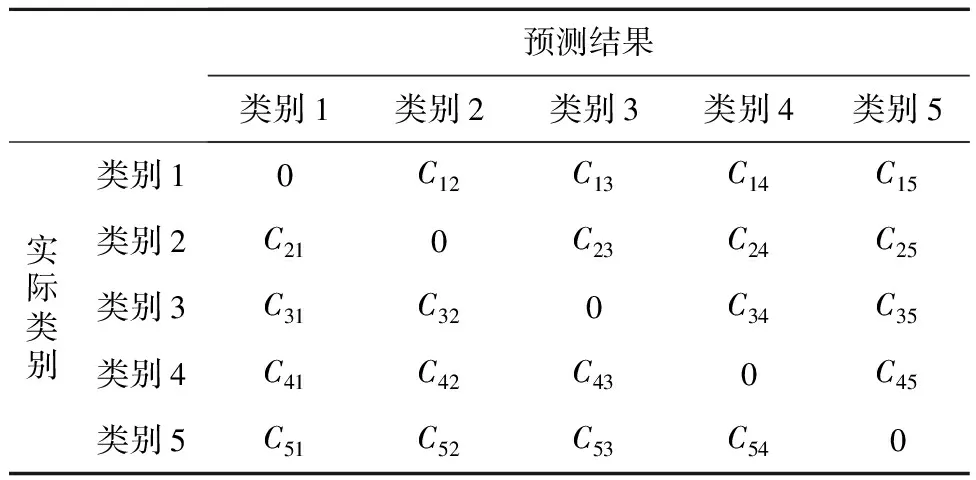
Table 1 Cost matrix with 5 types of data
(9)
其中,Ni表示i类数据实际样本量,Nj表示i类数据预测为j类的样本量。数据样本越少,被错分的代价越高。根据代价矩阵优化交叉熵损失函数,可得到具有代价约束的特征提取参数调整模型,如式(10)所示:
(10)
通过Cij降低少数类样本数据错分的概率,可使该类的数据特征更加敏感。
为了防止特征提取模型过度拟合,本文在代价函数中使用正则化方法优化权重参数,如式(11)所示:
(11)
利用L2正则化优化权重矩阵W,用正则化参数λ来控制权重惩罚力度,L是隐藏层的个数,ml是第l个隐藏层中神经元的数量。
通过最小化代价目标函数调整权重和偏置参数,可得到最优的SSAE特征提取模型,如式(12)所示:
(12)
3.2 代价约束算法步骤
为了解决算法初始化参数问题,CCA算法使用无监督学习预训练模型的较低层,为第1层网络生成初始参数,并将输出作为下一层的输入,最后通过贪婪的逐层训练得到SSAE中每层网络的初始参数。预训练后,使用有监督的反向传播学习对整个网络进行微调,可以减少重构输出与原始输入的误差。代价约束算法主要步骤如算法1所示。
算法1代价约束算法(CCA)
输入:预处理后的n维原始数据x,代价矩阵C。
输出:参数向量θ*,分类结果。
(1)Begin
(2)预训练得到初始化参数θ1=(W1,b1,W′1,b′1)。
(3)根据代价矩阵C最小化式(12)的目标函数,利用原始数据x和参数θ1计算隐藏层的输出h。
(4)训练得到下一层网络的参数θ2,计算第2个隐藏层的输出。最后训练得到初始化参数θ3。
(5)将提取的特征和重构数据输入分类器并惩罚分类结果。当数据被错分时,减少分类输出值:
y′i=yi-Cij×yi
当预测类为实际类时,增加分类输出值:
y″i=yi+Cij×yi
(6)反向传播调整误差,更新权重和偏置:
wij+lδyi←wij+Δwij←wij
bj+lδ←bj+Δbj←bj
(7)最小化目标函数值在几个时期内变化极小时,神经网络达到收敛,停止训练步骤。
(9)End
在步骤(5)中,CCA算法通过相应的成本对实际分类和错误分类都进行惩罚,yi是预测输出的类别,y′i是错误预测减少的新输出,y″i是实际类预测增加的新输出。因为预测类别输出的值越大,预测数据类别的概率越高,所以CCA算法的特征惩罚学习可降低错误分类的输出,提高数据类别检测的准确性。
在步骤(6)中,wij是第l个隐藏层中神经单元i到下一层神经元j的连接权重。δ是神经元的误差,反向传播过程主要通过误差调整2个参数值。
最后一层神经元误差由预测类的输出与实际类的输出决定,计算公式如式(13)所示:
(13)
同时,当i不是最后一层的神经单元时,计算误差要考虑2个连接单元的误差的加权和,如式(14)所示:
(14)
wik是神经元i到下一层神经元k的连接权重。预训练和微调可以降低训练深度模型的时间复杂度,提高模型的泛化性能。在AE的Softmax分类器中,根据算法1得到的最优参数,激活函数F(x)计算最大条件概率P(yi=j|xi;θj),输出x所属的类别。
(15)
4 仿真分析
4.1 数据集及仿真环境
经典的KDDCUP99数据集缺少新的网络攻击数据,与现有的网络流量存在较大差距,为此,澳大利亚网络安全中心创建了UNSW-NB15数据集[16],该数据集包含更多新的网络数据特征,可提高IDS评估的可靠性。UNSW-NB15数据集包含9个攻击类和1个正常类,共有44个数据特征,主要分为:时间特征、内容特征、流特征、基本特征、标记特征和其他原始特征。在257 673个数据样本中,有 175 341个训练数据和82 332个测试数据。具体的数据分布如表2所示。
实验环境的操作系统为Windows 10,CPU为Intel i5-8265U,主频为1.80 GHz,内存为8 GB,开发环境为Python。首先,根据数据分布对数据进行预处理,将所有的特征数据都转换为数值,再通过归一化处理将所有的属性值缩放到0~1,以加快模型的训练速度。采样数据时,选择80%的样本组成训练集,其余组成测试集,并将攻击类别分开进行平衡采样,这样可相对减少类不平衡问题的影响。

Table 2 Distribution of UNSW-NB15 dataset
4.2 评价指标
利用CCA算法从高维复杂数据中提取重要的约简特征,可得到最优的检测结果。为了评估算法的性能,使用准确率Acc、召回率R、精度Pre、F值和误报率FAR这5个指标来衡量入侵检测系统的优劣。Acc表示准确率,即正确分类的样本数的比例,是最常用的评价指标。召回率R表示正常样本数据被正确分类的比例。精度Pre表示预测的正样本数中正确分类的比例,精度高则误报率低。R和Pre都是重要的评估指标,为了综合考虑两者的影响,需要用调和均值F-measure来权衡。误报率FAR是预测的攻击样本中实际为正常数据的比例,降低误报率是IDS工作的重要方面。5个指标的计算方法如式(16)~式(20)所示:
(16)
(17)
(18)
(19)
(20)
其中,TP表示正常数据被正确分类的样本数,FP表示正常数据误报的样本数,TN表示攻击数据被正确分类的样本数,FN表示攻击数据漏报的样本数[6,15]。式(19)中的调整参数a是一个正值,用于确定精度在召回率上的相对重要性,在不平衡样本中将a设置为4可以减小FN。
4.3 检测精度分析
在两分类问题中,所有类型的攻击都被视为恶意事件,通过结合分类器可评估入侵检测算法的精度。为了验证CCA算法的普适性,本文同时采用标准UNSW-NB15 数据集和通用的KDDCUP99数据集进行标准化训练。使用5个度量指标分析正常数据和异常数据的检测结果,对比算法对异常数据的检测准确性。NDAE、FAE和CCA算法的性能指标如表3所示。

Table 3 Performance of three algorithms in two categories problems
在UNSW-NB15数据集上,CCA算法仿真检测数据的Acc和Pre都接近99%,验证了该算法可以准确预测正常流量数据和攻击数据。其次,FAE和 NDAE算法的FAR值为0.038和0.027,而CCA算法的FAR值减少到0.013。在对比的KDDCUP99数据集上,CCA算法的前4个指标基本达到99%,FAR值减少到0.009,说明该算法优化的分类器的误报概率更低,提高了入侵检测的可靠性。从训练结果可知,更复杂的UNSW-NB15数据集对算法的要求更高。
由于数据集中的攻击样本数远高于正常样本数,其他2种算法的两分类检测精度也很高,因此不能反映少数攻击类数据对IDS的影响。图3为不同算法在UNSW-NB15 数据集上的多分类混淆矩阵,0表示正常数据,1~9表示9种不同攻击类别。多类混淆矩阵可以更好地反映IDS的检测性能,评估特征提取算法对少数类别数据的影响。

Figure 3 Multi-class confusion matrix of different algorithms on UNSW-NB15 dataset
样本少的数据特征通常更难提取,所有算法对攻击类别的检测精度随着样本数量的减少逐渐下降。从图3 的混淆矩阵中可以看到,CCA算法对少数攻击类的识别精度更高,特别是对Shellcode和Worms的识别精度分别达到了80%和66%,说明CCA算法对少数类数据的特征提取更敏感。
4.4 收敛性分析
算法收敛时,IDS的检测精度能够直接反映特征提取算法的有效性。图4为不同算法性能随迭代次数变化的拟合结果,水平轴表示迭代次数,纵轴表示检测精度。

Figure 4 Detection accuracy when different algorithms converge on UNSW-NB15 dataset
在CCA、NDAE和FAE算法的拟合曲线中,检测算法收敛时分别迭代了35次,40次和45次左右。相比于另外2个算法,CCA算法以最快的收敛速度实现了最高的精度,表明该算法在IDS模型中要比其他算法的收敛性好。
生成入侵检测模型所需的训练时间会影响IDS的检测成本,为了在处理大规模数据时减少计算成本,需要控制算法的收敛时间。在SSAE深度学习中,隐藏层的神经元数量会影响模型的学习时间,模型训练时间随隐藏层神经元数量的变化如图5所示。从图5中可以看出,随着神经元数量增多,算法的时间复杂度增加,模型的训练时间变慢。但是,CCA算法通过数据降维来减少冗余特征,在UNSW-NB15 数据集上算法收敛速度仍比另外2个算法快,并且可持续减少模型所需的学习时间,执行速度分别是FAE和NDAE算法的1.35和1.10倍。训练KDDCUP99数据集也得到了相同的结果。
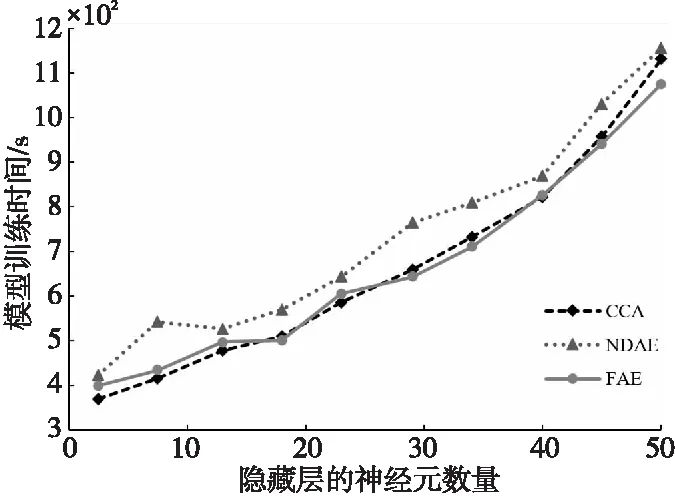
Figure 5 Model training time changes with network neuron numbers
5 结束语
在面临高维和复杂的网络入侵数据时,传统特征提取算法的性能达不到理想的效果,基于深度学习的CCA算法能更好地减少特征冗余并增强对少样本数据特征的敏感度。本文利用SSAE构建多层神经网络堆叠学习特征,通过KL散度对目标函数添加稀疏约束,最后结合代价矩阵训练特征提取模型的最优参数。仿真结果表明,CCA算法能够处理高维和类不平衡数据,精确提取重要的数据特征,使IDS具有更高的检测精度和效率。数据的不完整和噪声也会影响IDS的检测性能,下一步将深入研究如何提高数据特征学习的鲁棒性。

