区块链环境中基于局部敏感哈希的协同过滤推荐研究*
汪 静,钱晓东
(兰州交通大学经济管理学院,甘肃 兰州730070)
1 引言
随着数据的爆发式增长,数据挖掘的难度随之提高,导致数据使用者无法准确地获取想要的信息[1],于是推荐系统RS(Recommendation System)应运而生。RS通过分析用户的历史数据,推断出用户的潜在偏好,并据此进行准确的推荐。然而,推荐系统在某种程度上缺乏对用户信息的安全控制,违规违法使用个人信息的问题突出。目前,一个比较热门的思想是结合区块链和星际文件系统IPFS(Inter Planetary File System)来实现隐私保护,防止数据泄露。
IPFS是一种点对点的分布式文件系统,可以提供高吞吐量的内容寻址块存储模型[2]。Zheng等[3]提出了一种基于IPFS的区块链数据存储模型,在该模型中,矿工将交易数据存储到IPFS网络中,并将返回的交易IPFS哈希打包到区块中,大大减少了区块链数据。IPFS和区块链的结合,使得用户可以通过IPFS来处理大量数据,而不需要将数据本身存放在区块链中,只需将对应的加密哈希存储到区块链中并标记时间戳,这弥补了现有区块链系统在文件存储方面的短板。两者结合,可以很好地融合IPFS的永久文件存储和区块链的不可篡改、时间戳证明特性,能够满足分布式对等网络中各种用户的需求[4]。然而,由于区块链的开销隐含在交易和验证中,而推荐系统需要在对等体之间不断进行交互,从而在分散的环境中收集数据,其开销体现在实际的计算中,由此导致在区块链环境中进行推荐的效率较低[5]。同时,IPFS+区块链的使用也使得数据具有维度高、规模大和类型种类多的特点[6]。传统的近邻协同过滤推荐模型已经无法适应于这种环境,推荐效率不尽人意。
为了解决IPFS+区块链的环境中,RS效率低下,以及数据量大、维度高的问题,本文提出使用基于局部敏感哈希LSH(Locality Sensitive Hashing)进行协同过滤的推荐算法。本文在研究传统基于近邻的协同过滤技术基础上,使用优化后的LSH算法来获取用户的近邻集合,然后基于近邻用户集合的评分预测实现协同过滤推荐。该算法能够有效解决在IPFS+区块链环境中用户评分数据维度高、规模大而造成推荐效率低下的问题。
2 相关研究
2.1 关于区块链环境中的推荐研究
如今,RS的广泛应用在为企业和用户带来利益和便利的同时也缺乏对用户隐私的保护。虽然当前的一些法律法规要求服务提供商正确处理数据并确保用户的隐私,但Alneyadi等[7]通过调查指出仅靠立法并不能防止数据泄露,起到保护隐私的作用。因此,从推荐系统自身出发,确保其安全性成为当今学术界的一个研究热点。
区块链在协同过滤推荐文献中创建了一个新的范例,由于其固有的匿名、去中心化和不可篡改等特性,使过去无法实现的隐私保护成为可能。现有的基于区块链的RS主要是利用区块链安全和可验证存储的特点,达到在保持通信的同时降低计算成本的目的。Frey等[8]提出了一种基于区块链的RS,利用区块链基础架构解决RS中的隐私问题。作者声称他们为RS中的客户隐私提供了加密保证,因为原始数据只能被所有者访问。然而,他们仅是将区块链用作黑匣子,并没有进行有关架构的实验。Lisi等[9]提出了一个基于区块链的智能合约框架,并将该框架用作RS的外部模块,该方法可在一定程度上提高RS的透明性,防止大规模的负面评论攻击,但并不能防止消费者与商家之间的串通。
总体来说,目前针对区块链环境中的推荐研究还十分有限,大多都仅仅是提出了一些思路或运用了区块链的某一个特性,未进行深入研究,且都未解决在区块链环境中进行推荐所面临的效率低下以及数据规模大、维度高的问题。
2.2 关于局部敏感哈希的推荐研究
局部敏感哈希[10]是一种用于解决高维空间中近似近邻搜索的算法。Matsushita等[11]指出近似近邻搜索策略和最近邻策略相比,可以在保证一定准确性的情况下及时提供查询结果,避免大量资源的浪费,而LSH可以维护数据的局部性并支持近似近邻搜索。利用LSH来进行区块链环境中的近似近邻搜索具有很多优势。区块链环境中的项目数和用户数的快速增长以及数据之间的关联关系,使得RS所需要的数据维数增加。而基于LSH的方法处理高维数据具有较好的性能,同时该方法不需要维护全局信息,便于在分布式环境中实现,可以很好地适应区块链环境。
基于LSH面向区块链环境中的数据进行协同过滤推荐的关键点在于如何在降低额外的计算和存储开销的情况下,保证近似近邻搜索的高性能。在以往的研究中,Datar等[12]在局部灵敏哈希索引方法的基础上改进哈希计算的运行时间,从而可以无需嵌入即可在欧氏空间中的点上计算。Andoni等[13]提出了一种用于高维欧氏空间的近似近邻搜索算法,减少了查询时间和索引空间的开销。上述算法可以快速生成哈希函数,但是这些算法的哈希编码具有概率性,且分辨能力较低。He等[14]提出了一种可扩展哈希算法,为具有任何相似性函数的数据生成紧凑的哈希编码,尝试在保持数据相似性的同时,减少冗余的投影,从而优化搜索时间。以上算法都表明,要高效地获取近邻集合重点在加强LSH中哈希函数的相似度保持能力和独立性。此外,还有很多从不同角度提高LSH搜索性能的算法,如多比特[15]、多哈希表[16]和多探针[17]等算法。
以上算法从各个角度出发,都在不同程度上提高了LSH的搜索性能,但据了解目前还没有文献针对区块链环境中的LSH作出研究。区块链环境对LSH近似近邻搜索的效率和性能提出了更高的要求,并且其数据的高维特性也对协同过滤推荐算法提出了挑战。在传统LSH算法中,哈希函数的参数往往随机设置,从而需要使用大量的哈希表以保证查询的准确性,在区块链环境中便会增加存储和计算的开销。因此,本文在LSH的基础上,研究区块链环境中基于LSH的协同过滤推荐,将数据分布的主成分作为LSH机制中哈希函数的投影向量,量化每个哈希函数的权重;通过对哈希桶的间隔进行调整,并且根据冲突次数的大小进一步细化查询结果集,从而提高空间效率并在较少查询时延的同时保证查询准确性,然后采用加权方法预测评分,进而产生推荐结果。
3 基于LSH的近似近邻搜索分析
3.1 LSH近似近邻搜索算法
LSH是当前备受关注的近似近邻搜索技术,可以较好地解决传统近邻搜索存在的“维灾”问题,同时在很大程度上降低了近邻协同过滤的计算量。LSH的思想是将相似的对象以较大的概率哈希到同一个“桶”中,从而快速获取近邻对象。给定检索半径r和近似比例c(c=1+ε),ε为松弛变量且ε>0,假设U是哈希值的集合,O是数据对象的集合,且O⊂RD(RD为欧氏空间),u,v∈O,D(u,v)表示数据对象u和v之间的距离,H={h:O→U}是哈希函数的集合,对于∀u,v∈O有:
(1)如果D(u,v)≤r1,那么Pr[h(u)=h(v)]≥p1;
(2)如果D(u,v)≥r2,那么Pr[h(u)=h(v)]≤p2;
其中,Pr[·]是概率函数,表示u,v哈希值相等的概率,r1(r1=r)
为了直接处理欧氏距离,研究者提出了基于p-稳态分布(p-stable Distribution)的LSH[12]。
基于p-稳态分布的哈希函数族的定义如式(1)所示:

(1)

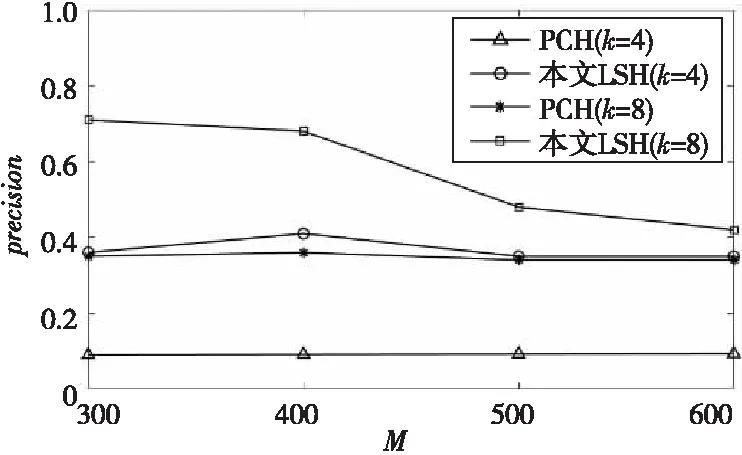
设fp(t)代表p-稳态分布的概率密度函数的绝对值,定义d=‖v1-v2‖p,那么向量v1,v2被映射到一个随机向量a上的距离是|a·v1-a·v2| p(d)=Pr[ha,b(v1)=ha,b(v2)]= (2) 根据式(2)可以看出,对于固定的W,2个向量的冲突概率随着距离d的增加而减小。 LSH将数据集从高维空间投影到低维空间,认为在高维空间中相近的点在随机投影中的位置也相近。但是,由图1可以看出,u为随机投影方向,将数据点从二维空间投影到一维空间,查询点o1的最近邻点由o3变成了o2。因此,在实际应用中,需要考虑使用一组函数而非单个函数进行比较。G={g:RD→Uk}是一组复合LSH函数,其中∀gi∈G由H中随机选择的k个哈希函数序列组成,即: gi(o)={hi1(o),hi2(o),…,hik(o)} (3) 其中,hij都是从H中独立且随机地选取的。 Figure 1 A point set in a bad projection direction 传统近邻搜索的主要方法是基于空间划分的算法,如R树、k-d树(k-dimensional树)。这些算法虽然可以得到精确的查询结果,但在高维数据集上的效率却尤其低下。Weber等[18]通过实验证明,在维度高于10之后,基于空间划分的搜索技术都退化为线性搜索。传统近邻搜索方法通常无法适应区块链环境中的数据维数高、规模大的特点,而近似近邻搜索可以很好地解决这一问题。虽然近似近邻搜索牺牲了一部分精确度,但其通常能在很小的时间复杂度下得到近似精确甚至精确的搜索结果,这更能满足区块链环境的实际需求。 Dater等[12]通过实验证明了处理高维数据集时,LSH算法相对于传统近邻搜索算法所展示出来的优越性,为本文研究区块链环境中的协同过滤推荐提供了思路。 在实际应用中,LSH算法包含哈希表的个数和哈希函数的个数这2个主要参数。为了保证查询的准确性,往往使用过多的哈希函数和哈希表,从而使得空间和时间效率变得低效。 当在区块链环境中使用LSH进行近似近邻搜索时,为了维护数据局部性并保证查询准确性,LSH算法不得不使用大量哈希表和哈希函数,这无疑增加了区块链环境中近似近邻搜索的计算开销,导致系统的空间效率低下。同时,传统LSH算法及其改进算法大多并未考虑数据分布,直接随机选择哈希函数的投影向量。在理想情况下,数据点均匀分布,它们被散列到哈希桶中的概率相同,因此桶中的点是均匀的。然而,在区块链环境中数据的分布很大概率并不均匀[19]。因此,通过随机选择的投影向量对不均匀分布的数据点进行哈希会导致许多不相关的数据点聚集在相同哈希桶中,从而降低查询结果的准确性。 针对上述问题,本文提出运用数据分布的主成分来分配LSH算法中的投影向量,从而使用少量哈希表在区块链环境中实现近似近邻搜索,降低空间开销。同时,为了提高查询准确率并减少距离计算的时间开销,优化后的LSH量化了哈希表中每个哈希函数的权值并调整哈希桶的间隔值,在没有任何精度损失的情况下进一步记录候选点的冲突频率,以减小查询结果集的大小。 主成分分析已经成为了一种应用广泛的降维方法,其主要思想是用少数几个新的变量代替原有变量,在减少需要分析的数据的同时,尽量减少原始数据所包含的信息的丢失。具体到本文的应用中即通过主成分分析,在降低数据维度的情况下,保持投影向量的最大标准差。利用数据集的协方差矩阵得到投影向量的特征向量和特征值,将体现数据分布的前几个特征向量作为LSH中的投影向量并构造哈希表,有效地减少空间开销。 假设高维特征数据集R中的τ个元素均为n维向量,用矩阵表示如式(4)所示: (4) 其中,ui表示用户i的评分向量,rij表示用户i对项目j的评分。 为了保证所有维度上的偏移都是以零为基点的,将样本去中心化,如式(5)所示: (5) (6) 对协方差矩阵S进行特征值分解得到特征向量集合P和特征值集合N,选取最大的m(m=kl,其中,k表示每个哈希表中哈希函数的个数,l表示哈希表个数。)个特征值对应的特征向量作为数据集的主成分组P′,通过P′映射将高维特征数据集R表示为数据集R′,且R′=RP′。由于特征值越大,其所对应的特征向量携带的信息越多,所以将前几个特征向量作为LSH近似近邻搜索中的投影向量,可以有效地减少空间开销。 4.1.1 基于特征值优化的投影向量权重 传统LSH算法中数据点在哈希表中的哈希值是通过给哈希函数赋予一个随机权重值并进行加权计算得来的。根据式(3),对于∀v∈O,该点在第i个哈希表中的哈希值如式(7)所示: gi(v)=ai1hi1(v)+ai2hi2(v)+…+aikhik(v) (7) 其中,aij是一个(0,1)随机选择的常数且服从p-稳定分布,同时1 传统LSH算法通常为哈希函数随机分配权重值,这会影响查询的效率及性能,为了获得更好的搜索结果,算法应该为具有更好投影向量的哈希函数分配更大的权重。本文算法将特征值进行排序,利用排序靠前的特征向量作为投影向量,这样可以更好地反映不同向量在方向上的贡献。 4.1.2 基于特征值优化的桶间隔 在传统LSH算法中,W是一个常数,因而很容易被忽略。然而实验证明,W的大小会影响整个近邻搜索系统的性能。当W较大时,相邻的点有更大的概率被哈希到同一个桶中,但同时也增大了将相距较远的点哈希到同一桶中的概率;当W较小时,虽然相隔较远的点很难被哈希到同一个桶中,但也增大了2个相邻的点被哈希到不同桶中的概率。 优化后的LSH将特征值按大小排序,并将其对应的特征向量按顺序选为投影向量。第1个特征向量方差最大,其余依次减小,方差越大的特征向量可以以较大的概率将距离较远的点哈希到不同的桶中。为了使方差较小的主成分也保持这一属性,优化后的LSH调整并减小方差较小的主成分所在哈希函数的间隔值W。同一哈希表中的哈希函数间隔值W相同,并且相邻2个哈希表中哈希函数的间隔之比与特征值之比相等。也就是说,对于第i(i=1,2,…,l)个哈希表,其哈希函数的间隔值Wi如式(8)所示: (8) 其中,W0为初始默认值,大量实验表明,当W0=4时,检索效果较好[20];λ1代表最大特征值。 4.1.3 基于冲突次数的结果集优化 在LSH中,2个相距较远的点也有很大概率会在某个哈希表中发生冲突。因此,如果结果集中包含了所有与查询点q冲突的点,在进行距离计算时,由于大量与查询点q冲突次数较少的无关点的存在,会增加计算开销并降低查询的精度。 为了精炼结果集C(q),提高计算效率,优化后的LSH在执行哈希计算时记录候选点与查询点q在l个哈希表中的冲突次数。一般来说,候选点q与查询点的冲突次数越多,该候选点是查询点q的近似近邻的概率也越大,将候选点p与查询点p的冲突次数用conf(p)表示,其计算方式如式(9)所示: (9) 假设t为冲突阈值,如果候选点p的冲突次数conf(p)≥t,则称点p为频繁冲突点。由于第1个哈希表中的哈希函数是特征值较大的主成分,那么表中与查询点q发生冲突的候选点很大概率上属于查询点q的近似近邻,因此算法将第1个哈希表中与查询点q发生冲突的点都保存在其候选集C(q)中。在其余哈希表中,只有conf(p)≥t时,才将点保存在C(q)中。如果存在某个频繁冲突点p与q的距离小于或等于距离阈值M,则可以提前终止检索。 给定p1=p(r),p2=p(cr),令α,β,δ分别为冲突阈值的百分比形式、误判率和错误率。对于p2<α (10) p(s)的定义如式(11)所示: (11) (12) 将式(12)代入l1,可得: (13) 根据α和l的取值,可以确定冲突阈值t的取值如式(14)所示: (14) 根据以上分析,优化后的近似近邻搜索算法的精确率由误判率β、近似比例c和错误率δ决定,这3个参数均为用户自定义的常量。其中δ决定了所有基于LSH近似近邻搜索算法的成功率。c越小,精确率越高;β越大,进入候选集的频繁候选点就越多,搜索质量也随之越高,但同时也会带来更大的距离计算开销。本文依据现有方案设置δ=1/e,β=100/s(其中s为数据点的数量)。 4.3.1 查询精确度 哈希表的数目是一个LSH算法中非常重要的参数,需要选取一个合适的值使得以下2个性质同时成立: P1:如果存在一个对象o使得它与q的距离小于或等于r,则o是一个频繁冲突对象。 P2:误判对象的总数目小于βs,其中每个误判对象都是一个与q的距离大于cr的对象。 本文算法可以保证选取的l能以至少(1/2-δ)的概率使得以下2个性质同时成立。 证明假设S1表示那些与查询点q的距离小于或等于r的频繁冲突的对象,即S1={p|conf(p)≥αl∧‖p-q‖≤r}。对于∀p∈S1有: Pr[P1]=Pr[conf(p)≥αl]= 其中,pconf=Pr[|haj(p)-haj(q)|≤Wr/2],Yi~B(l,1-pconf),j∈{1,2,…,l},pconf≥p1>α。 设有l个伯努利随机变量Yi,1≤i≤l。若2个对象之间没有发生冲突,则令Yi=1,即Pr[Yi=1]=1-pconf;若2个对象发生冲突,则Pr[Yi=0]=pconf。综上,随机变量Yi的期望E[Yi]=1-pconf。 Pr[Y-E[Y]≥γl]=Pr[Y≥(1-α)l]≤ 因为conf(p)≥αl,即p和q发生冲突的概率小于或等于(1-α)l,所以: Pr[P1]=Pr[Y≤(1-α)l]= 1-Pr[Y>(1-α)l]≥1- Pr[Y≥(1-α)l]≥1-e-2l(p1-α)2≥1-δ 假设S2表示那些与查询点q的距离大于或等于cr的频繁冲突对象,即S2={p|conf(p)≥αl∧‖p-q‖≥cr},同理可得: Pr[P2]=Pr[|S2|<βs]=1- 由于优化后的算法只有在满足P1或P2其中之一时才停止,那么, Pr[P1∩P2]=Pr[P1]+Pr[P2]- 由此得证。 □ 4.3.2 时间复杂度 在建立索引阶段,根据哈希表个数,需要进行y次运算,每次循环分别需要计算k次、k-ky次、k-1次,因此总的复杂度为O(y)*O(k+(k-ky)+(k-1))=O(l)*O(3k-ky-1),其中,k表示每个哈希表中哈希函数的个数,y表示哈希表个数。优化后的算法复杂度相对较低,可以使用较少的哈希表和哈希函数找到查询点的近邻节点,在第6节的实验分析中,将对此进行验证说明。 基于以上分析,本文提出的基于优化后的LSH的协同过滤推荐算法的具体步骤如下所示。 步骤1生成用户-项评分矩阵Dm×n。 依据用户评分的多条记录,将其转变为用户-项目评分矩阵Dg×h。该矩阵的行表示g个用户,列表示h个项目,矩阵分量Dij表示用户i对项目j的评分。若未评分,则Dij=0。 步骤2产生用户近邻集合。 (1)建立LSH索引。 (2)近似近邻查找。 遍历待查询高维数据点x所在的所有哈希桶,并获得其所有的近似近邻。首先在第1个哈希表中查找查询点x所在哈希桶,将桶内所有数据点存储在结果集中。然后从第2个哈希表开始,利用式(9)记录与数据点x冲突次数达到t次以上的点,并将该点存储在数据集中。最后将得到的结果集中的点x′与查询点x进行比较,如果距离大于r即D(x,x′)>r,则将该点从结果集中删除,从而获得数据点x的所有近似近邻结果集。 步骤3预测用户评分,并产生推荐。 首先,根据上述算法得到的最近邻用户集合,利用式(15)计算目标用户与近邻用户之间相似度,通过式(16)的加权平均策略进行评分预测,得到用户对未评分项目的预测评分;然后,依据用户评分的高低,产生项目推荐列表。 (15) 其中,ζ为常数1,当用户u和用户υ的欧氏距离为0时,用户间的相似系数为1。 (16) 为了评估优化后的近似近邻搜索算法的性能,本文进行了如下实验。 6.1.1 实验设置 实验仿真环境的计算机配置为:Windows 10操作系统,8 GB内存,Intel(R)Core(TM)i5-8265U,CPU为主频3.90 GHz。 为了更加贴合区块链环境中数据高维、非均匀分布等特点,本文选用数据非均匀分布的LabelMe数据集进行实验,从该数据集的图像中提取了20 000个512维的特征点,且将前1 000个特征点用于查询。 近似近邻搜索的性能与其距离阈值相关联,但由于LSH的不确定性和概率性质,很难确定近似近邻查询中的最优距离阈值。为此,Dater等[12]提出利用采样机制来获取适当的距离阈值。在实验中分别选取300,400,500,600来测试优化后的LSH性能,从查询精确率和平均查询时间两方面,通过与将PCA(Principal Component Analysis)和LSH结合的PCH(Principal Component analysis locality sensitive Hashing)进行对比,来衡量优化后的LSH算法的性能。 6.1.2 实验结果及分析 (1)精确率。 精确率是评价查询结果精确性的指标,它表示预测为正的结果中有多少是正确的。点q的近似近邻查询结果的精确率由式(17)计算而来: (17) 其中,TP和FP分别表示预测正确和预测错误的样本数量。 与传统的LSH算法相比,本文所提出的优化算法通过考虑数据分布的主成分,可以使用较少的哈希函数就能以较大概率将相近的点映射到同一桶中。同时为了精炼查询的结果集,本文的优化算法对桶间隔进行了优化,并通过对候选点的冲突次数进行统计,显著减少不相关点的数量,从而达到提高查询精确率的目的。本节中M均表示距离阈值。 图2反映了当k=4和k=8时,即每个哈希表中有4个和8个哈希函数时,在LabelMe数据集测试中各方案的查询精确率。可以看出,当k=4时本文优化后的LSH的查询精确率相比于PCH提高了大概30%;PCH算法在k=8时的查询精确率甚至不如优化后的算法在k=4时的精确率;当k=8时,优化后的LSH算法就已经能够获得较高的查询精确率了。 Figure 2 Comparison of query precision (2)平均查询时间。 传统的LSH通过随机选择投影向量对数据点进行映射,从而导致哈希桶中增加了许多无关数据点,使得候选结果集较大,增加了后续的计算开销。PCH虽然缩减了候选结果集的大小,但其由于主成分分析所带来的正交性约束问题仍然存在。本文所优化的算法不仅解决了该问题,并且通过对冲突次数的统计,进一步精炼了候选结果集,从而在很大程度上降低了计算开销。 各个算法执行1 000次近似近邻搜索的平均时间开销结果如图3所示。 Figure 3 Comparison of average query time per 1 000 queries 从图3可以看出,无论在k=4还是k=8的情况下,优化后的LSH算法的查询时间都远远低于PCH算法的。当k=4时,在每1 000次查询中,本文优化后的LSH算法与PCH算法相比,其查询时间几乎减少了80%。本文算法和PCH算法在进行近似近邻搜索时,都需要进行哈希计算和距离计算,与PCH算法不同的是,本文的LSH通过调整每个哈希函数的权重和桶间隔,可以在很大程度上减少哈希计算量,从而降低整个查询过程的时间开销。 6.2.1 数据集与评价指标 本文数据集采用MovieLens 1M电影评价数据集,仿真前对数据集进行预处理,剔除了部分数据,最终包含6 040位用户对3 900部电影的744 398个评分数据,评分分值为1~5。 为了解决区块链数据的存储问题,在应用场景中,可以使用分布式存储(如IPFS)将数据的哈希值录入区块,该方案可以将用户的评级有效存储在数据库中。在存储于区块链的每项事务中,用户附加了一些元数据,这些元数据即他们评级的哈希值。一旦用户想要获取推荐,他就会收集相应的事务并提取元数据。Casino等[5]的研究表明,通过运用该方案的数据整合,可以在区块链环境中使用MovieLens数据集进行实验仿真。 本文实验结果主要包含推荐精度与推荐效率2部分。在推荐效率方面,本文通过不同邻居数量时的算法运行时间来展示本文推荐算法的效率,运行时间能够反映算法的时间复杂度和实效性。此外,本文将均方根误差(RMSE)作为推荐质量的评价指标,利用算法预测出的评分和用户的真实评分之间平方差异平均值的平方根来衡量推荐的精确度,该值越小,说明算法推荐质量越好。RMSE计算如式(18)所示: (18) 6.2.2 实验结果与分析 (1)参数分析。 本文算法是一种针对区块链环境中高维大规模数据的推荐算法,而LSH中哈希表个数l和哈希函数个数k可以限制或放宽对近邻用户的搜索条件,影响用户数据映射的哈希值,从而影响相似用户集合,进而影响协同过滤推荐算法的性能。本实验研究了l,k取值对算法性能的影响,l和k的取值都从2到10不等,其结果如图4所示。 Figure 4 Impact of l-k on recommendation quality 从图4中可以看出,随着l的增大,RMSE总体呈现增长的趋势;随着k的增大,RMSE逐渐减小。这是因为在本文算法中,近邻用户集合是不同哈希表中近邻用户集合的并集,随着l的增大,不相似的用户进入集合的概率也随之增大,而这些不相似的用户会干扰预测的准确度,因此为提高预测准确度,在实际应用中应该适当选取较小的哈希表个数。随着k的增大,减小了不相似用户被映射到同一哈希桶的概率,这样就保证了基于这些大概率上的相似用户推荐结果的准确性。在后面的实验中,考虑到数据集大小以及实际运行内存大小,本文设定参数k=10,l=10,并且选取均方根误差(RMSE)作为推荐质量的评价指标,以查找不同邻居数目时算法的运行时间作为运行效率的评价指标,然后对不同推荐算法的推荐质量和运行效率进行比较。 (2)不同推荐算法运行效率对比。 为了验证优化后的推荐算法在实际运行中的高效性,实验选取基于PCH和基于E2LSH(Exact Euclidean LSH)的协同过滤算法进行了对比研究。图5为3种推荐算法在不同邻居数目时的运行时间的对比情况。 Figure 5 Comparison of the running time of the algorithm in this paper and other collaborative filtering algorithms 如图5所示,随着邻居数目的增加,3种推荐算法的运行时间都有不同程度的增加,但总体来说本文算法的运行时间更为稳定,并且远远低于其他2种协同过滤推荐算法的,表明了本文算法的高效性和稳定性。从整体走势来看,3种推荐算法均出现了较大程度的起伏,这主要是因为LSH是一个概率算法,相似度用户集合中的用户只是极大概率的相似用户,并不能保证是准确的相似用户,所以会导致预测准确度的变化。 本文算法通过对数据的降维,有效降低了高维数据集上由于索引结构导致的数据挖掘算法的性能下降问题,并且利用数据分布的主成分选取投影向量,并重新分配投影向量的权重,这样能够在很大程度上减少需要使用的哈希函数的个数,从而减少计算开销。基于E2LSH的协同过滤算法利用随机投影向量来映射数据点,使得在近邻搜索过程中,候选集中增加了额外的无关数据点,从而使后续的距离计算增加了时间开销。基于PCH的协同过滤算法虽然也利用了数据分布的特性,但传统主成分分析的正交性约束使其无法获取连续的投影向量,也无法对不相关点进行有效的消除。因此,本文算法提出利用主成分相应的特征值对哈希函数的权重进行量化,并调整桶间隔,通过对冲突频率的统计精炼结果集,在很大程度上减少了相似度的计算,降低了算法的时间复杂度。相较于以往的推荐算法,本文算法能够更好地适用于高维以及不同规模的数据集,能够在较短的时间内作出推荐。 (3)不同推荐算法预测准确度对比。 为了测试本文推荐算法的推荐质量,本文将基于优化后的局部敏感哈希的协同过滤算法与其他协同过滤算法进行了对比分析,主要比较不同的邻居数目的推荐效果,对比结果如图6所示。 Figure 6 Comparison of recommendation quality between this algorithm and other collaborative filtering algorithms 如图6所示,随着邻居节点数目的增加,3种算法的推荐质量都有所提高,但本文算法的RMSE一直处于较低的位置,并且随着邻居数目的增加逐渐趋于稳定。这意味着相比于另外2种协同过滤算法而言,本文算法具有更高的推荐精度,表明本文算法在减少计算开销的同时,很好地维护了数据的局部性,通过考虑数据分布的特性,在使用少数哈希表的情况下就能得到近邻结果,从而保证了推荐结果的准确性。 综合考虑时间消耗和预测准确度,在处理高维大规模的数据时,本文算法是一个既可以快速响应用户需求,又可以提供较好预测结果的算法。 针对在区块链环境中进行协同过滤推荐时,由于数据规模大、维数高对推荐质量产生的影响,提出了局部敏感哈希的协同过滤推荐算法,利用优化后的LSH获得用户近邻集合,进而形成推荐结果。 实验结果表明,优化后的LSH仅需要少量的哈希表和哈希函数就可以获得较为精确的近邻搜索结果,且搜索效率有很大的提高。将优化后的LSH应用到区块链环境中的协同过滤推荐时,可以很好地应对区块链中数据特点所造成的问题,缓解了高维大规模数据对推荐性能的影响,在一定程度上提高了推荐质量和效率。由于该算法性能主要依赖于关键参数的选取,且对参数比较敏感,部分人为设置的经验值在不同程度上对推荐效果都有影响,因此如何调整参数的最优配置,是下一步工作的研究方向。
3.2 算法分析
3.3 在区块链环境中存在的不足
4 基于数据分布的LSH优化及分析
4.1 主成分分析

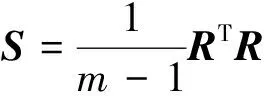

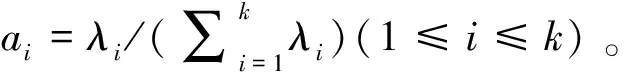

4.2 参数设置分析


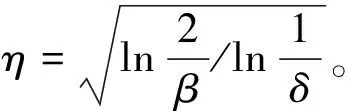

4.3 优化后的LSH算法的理论保证


5 协同过滤推荐算法


6 实验模拟分析
6.1 优化后的LSH近似近邻搜索算法实验分析

6.2 优化后的协同过滤算法实验分析



7 结束语

