齐次多项式正定性的新判定准则

赵鹏程,王 峰

(贵州民族大学 数据科学与信息工程学院,贵州 贵阳 550025)

结构张量在图像处理、医学降噪和弹性摩擦等问题中有着重要应用价值.[1-4]尤其是H-张量,因其在数值分析上的重要作用,其理论、性质及迭代算法受到众多学者的广泛研究.[5-10]同时,多元偶次齐次多项式在诸多问题中有着广泛的应用,[11-18]其正定性的判定受到越来越多的关注.本文借助H-张量来判定齐次多项式的正定性,并用数值算例表明了所得结论的有效性．

1 预备知识

用R(C)表示实(复)数集,N=[n]={1,2,…,n} .m阶n维实(复)张量A=(ai1i2…im)由nm个实(复)元素构成,其中ai1i2…im∈R(C),ij∈N,j∈[m].对m阶n维张量A=(ai1i2…im),若存在数λ和非零向量x=(x1,x2,…,xn)T∈Cn,使得Axm-1=λx[m-1],则称λ为A的特征值,x为对应于λ的特征向量,其中Axm-1和x[m-1]的第i个分量分别是:

若ai1i2…im=aπ(i1i2…im),∀π∈Πm,则称A=(ai1i2…im)是对称的,其中Πm为m个指标的置换群.称I=(δi1i2…im)为单位张量,其中:

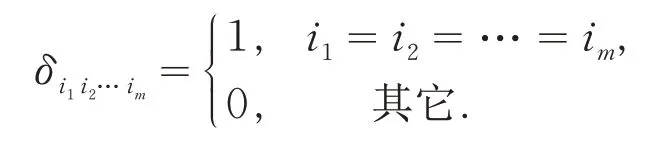
设f(x)是一个m阶n次齐次多项式,其中:

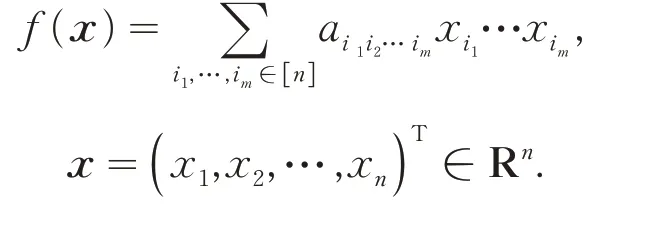
若对:

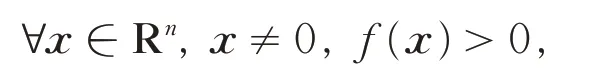
则称f(x)是正定的.f(x)可表示为m阶n维对称张量A与xm的乘积,[1]如:

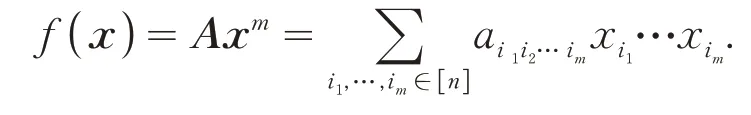
当f(x)是正定时,对称张量A也是正定的.

定义1[7]设A=(ai1i2…im)是m阶n维张量,若存在正向量x=(x1,x2,…,xn)T∈Rn,使得:

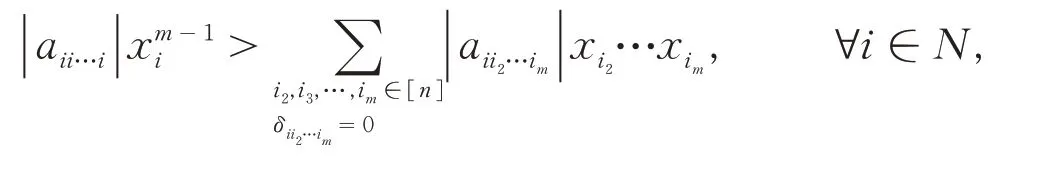
则称A是H-张量.

定义2[4]设A=(ai1i2…im)是一个m阶n维张量,若存在非空子集I ⊂N,使得:

则称A是可约的.否则,称A是不可约的.

定义3[8]设A=(ai1i2…im)是一个m阶n维张量,若存在指标k1,k2,…,kr,使得:

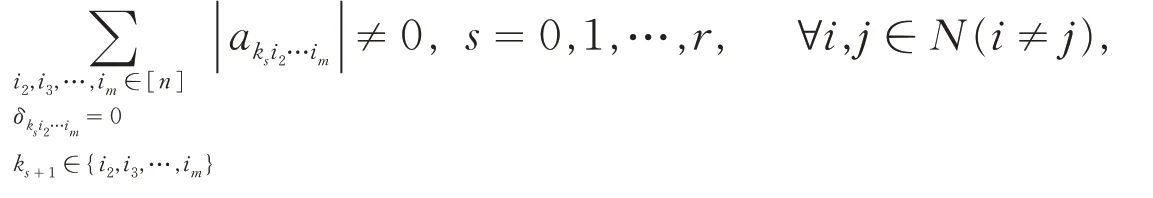
其中k0=i,kr+1=j,则称A中有一条从i到j的非零元素链.

引理1[5]若A=(ai1i2…im)是严格对角占优的,则A是H-张量.

引理2[9]设A=(ai1i2…im)是m阶n维张量.如果存在正对角矩阵X,使得AXm-1是H-张量,则A是H-张量.

引理3[5]设A=(ai1i2…im)是m阶n维张量且不可约.若:

且至少有一个严格不等式成立,则A是H-张量.

引理4[8]设A=(ai1i2…im)是m阶n维张量.若:

(i)|aii…i|≥ri(A), ∀i∈N;

(ii)N3={i∈N:|aii…i|>ri(A)}≠∅;

(iii)∀i∉N3,从i到j存在一个非零元素链,使得j∈N3;

则A是H-张量.

2 主要结果

给出如下记号:设A=(ai1i2…im)是一个m阶n维张量,记:

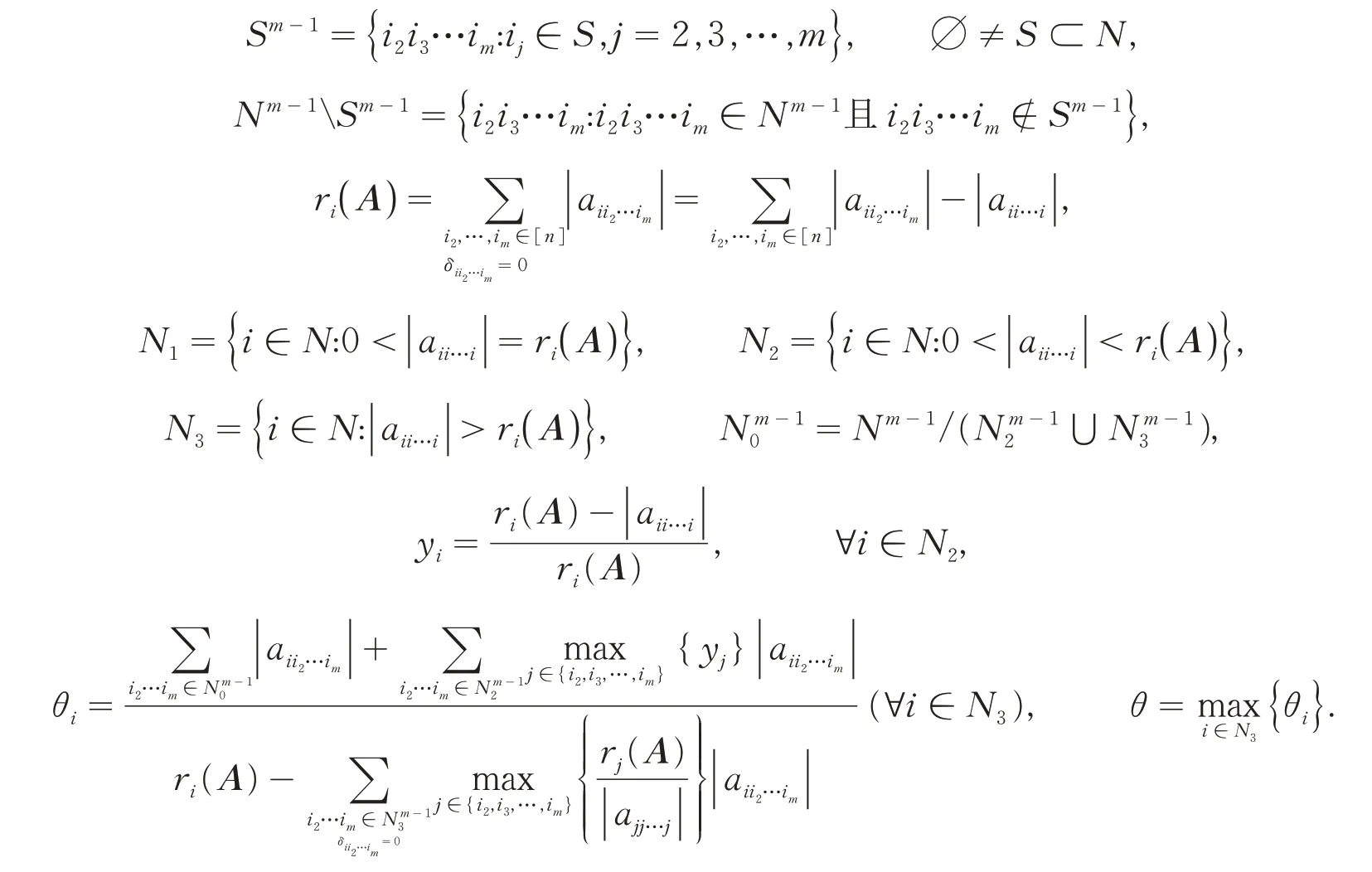
下面,给出H-张量新的判定不等式.

定理1 设A=(ai1i2…im)是一个m阶n维张量.若:

则A是H-张量.

证明:设:

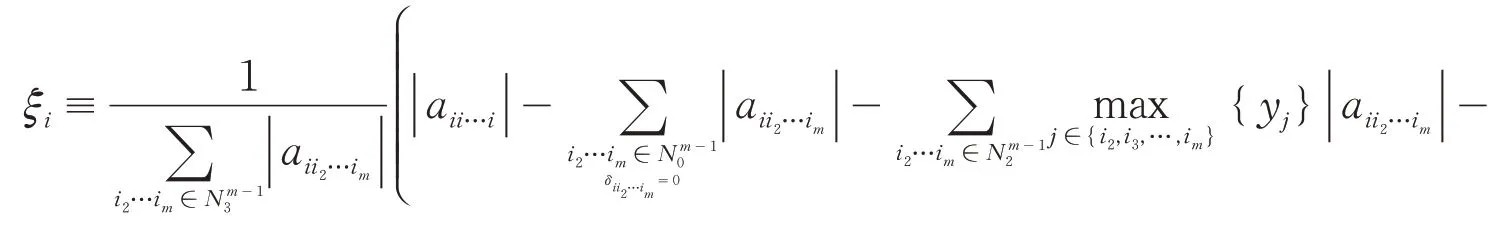
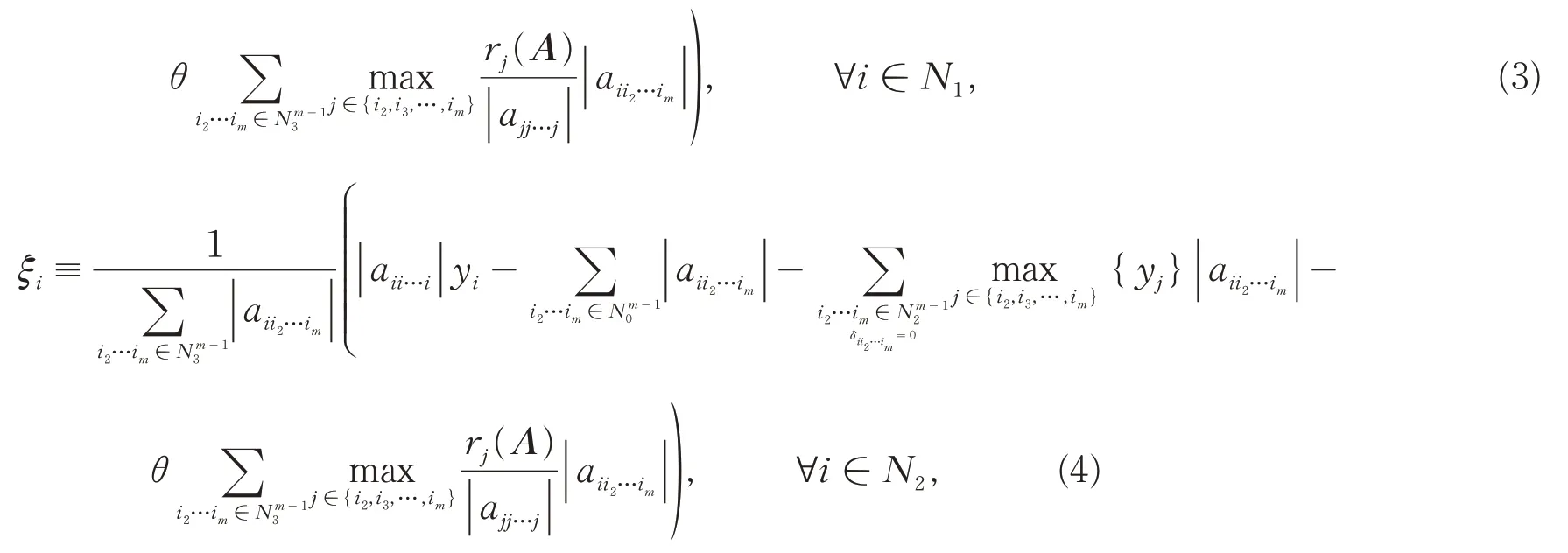
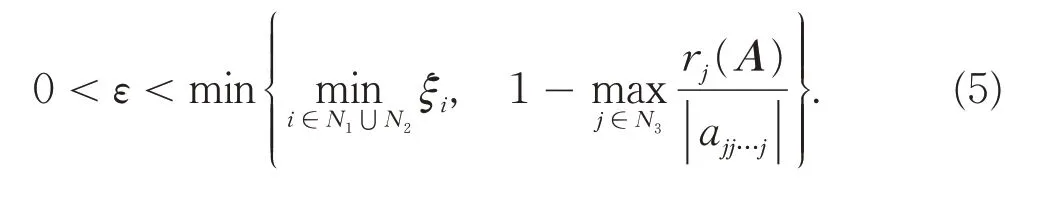
构造正对角阵D= diag(d1,d2,…,dn),记B=ADm-1=(bi1i2…im),其中:

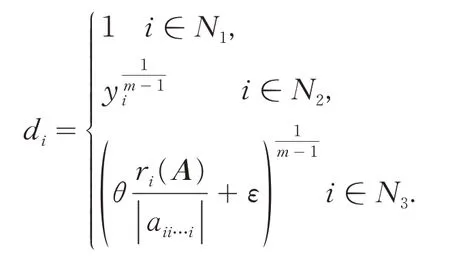
由yi,θ及ε的定义知di< 1(i∈N2∪N3).下面,证明B是严格对角占优的.

(i)对∀i∈N1,当时,由(1)式得:

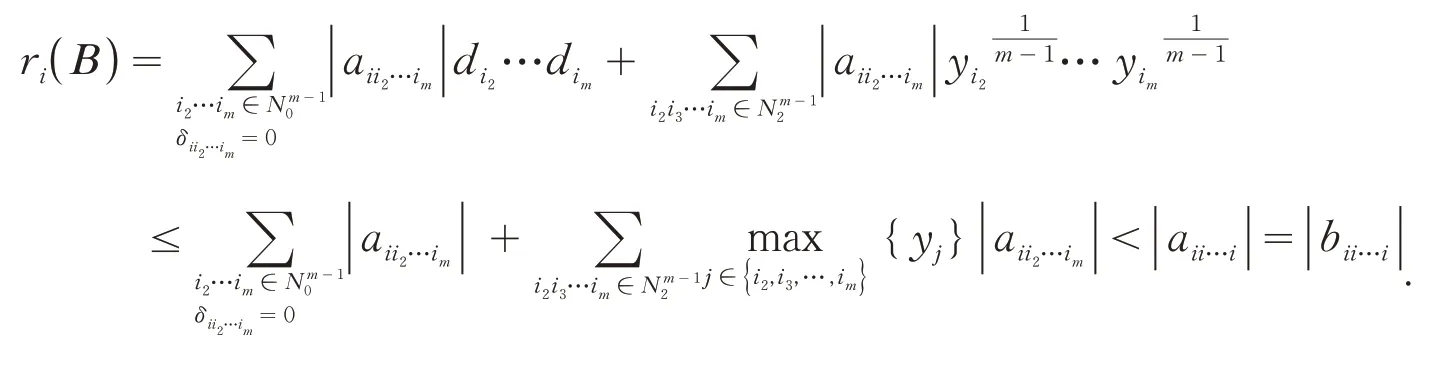
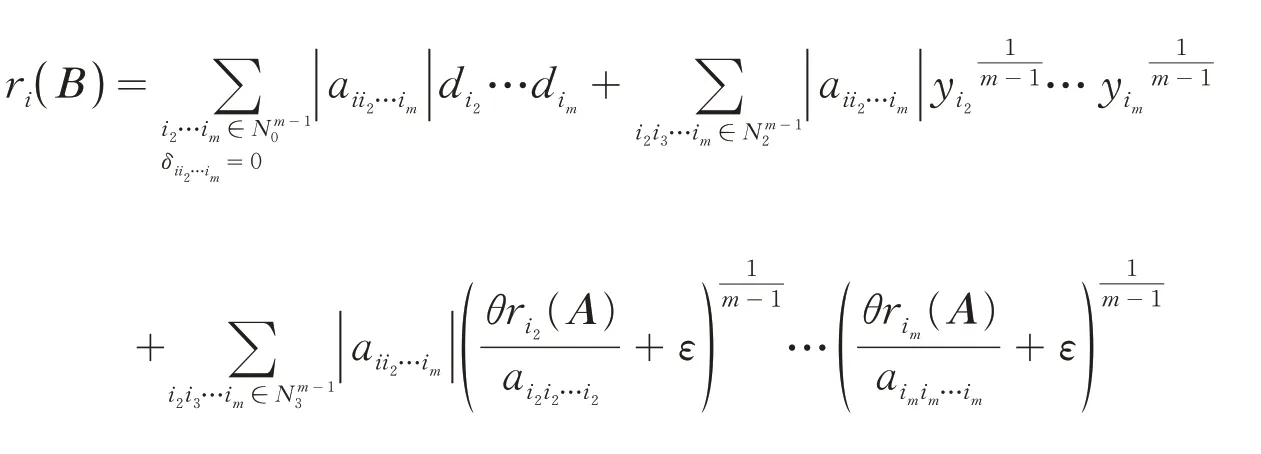
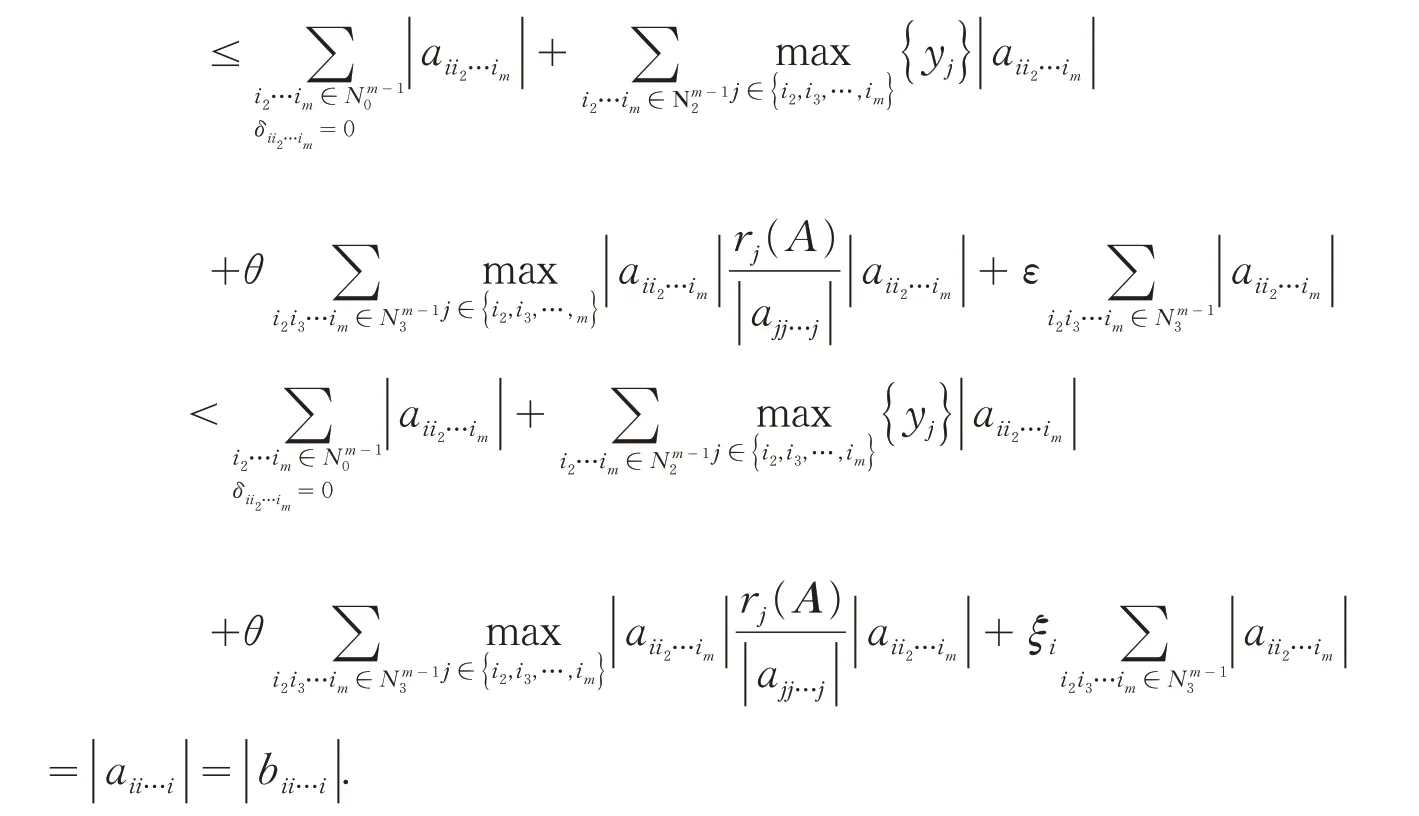
(ii) 对∀i∈N2,当时,由(2)式可得:

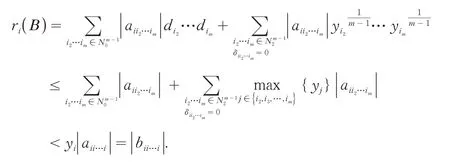
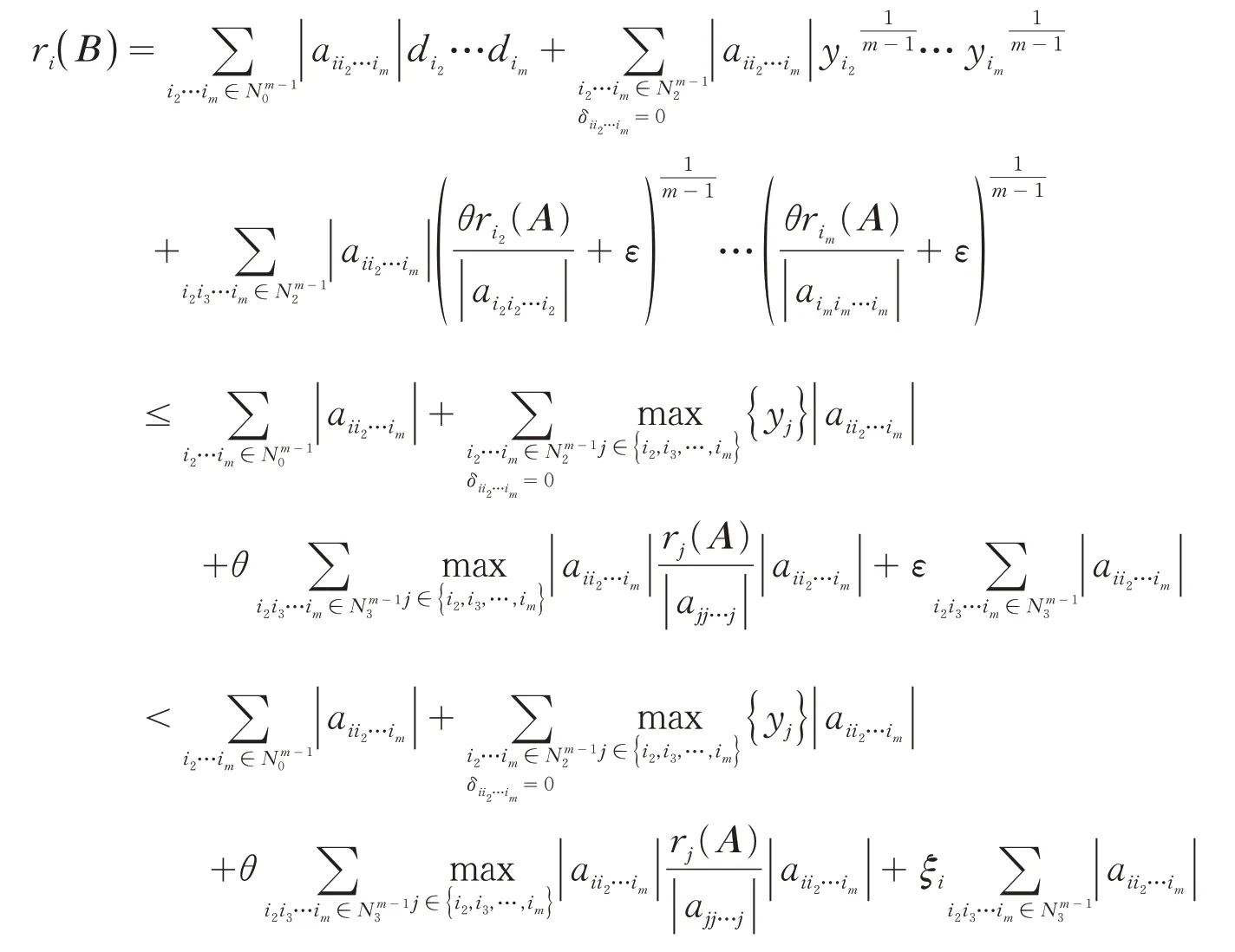
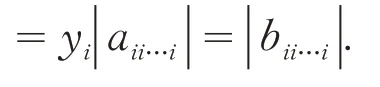
(iii) 对∀i∈N3,由θ的定义知:

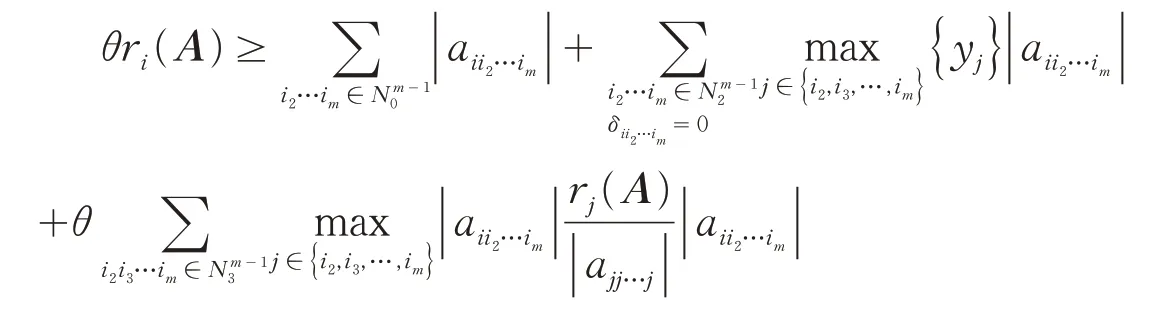
从而:

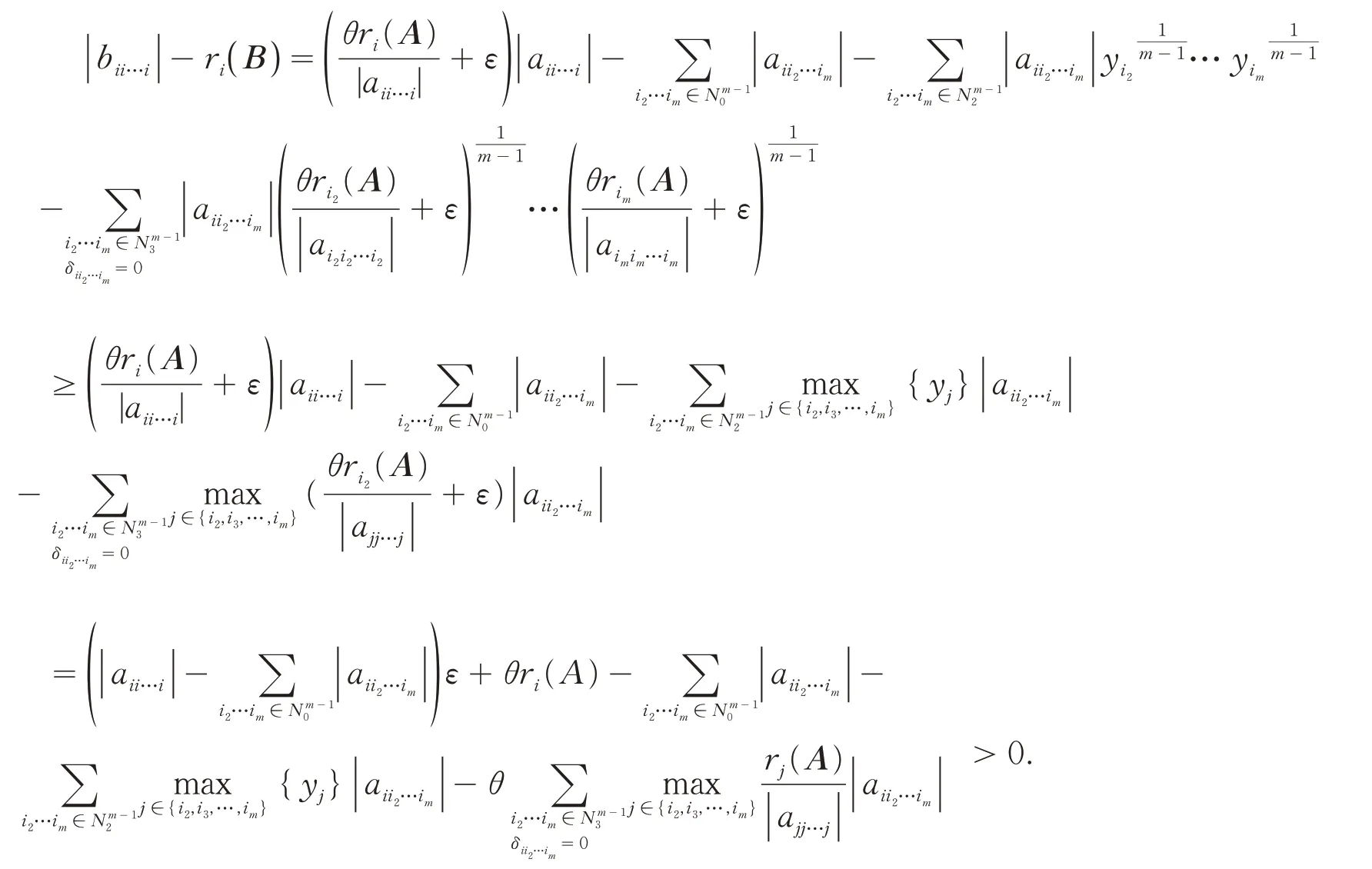
综上可知,|bii…i|>ri(B)(∀i∈N).由引理1知B是H-张量.进而,由引理2知A是H-张量.

定理2 设A=(ai1i2…im)是一个m阶n维的不可约张量.若:

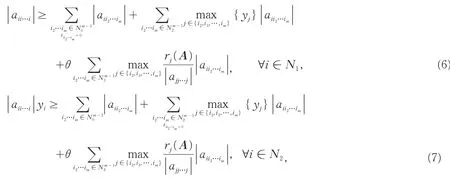
且(6)和(7)式中至少有一个严格不等式成立,则A是H-张量.

证明:由A不可约知:

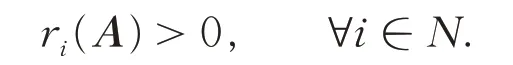
构造正对角阵D= diag(d1,d2,…,dn),记B=ADm-1=(bi1i2…im),其中:

由yi及ε的定义知di< 1(i∈N2∪N3).下面证明B是严格对角占优的.

(i) 对∀i∈N1,

(ii) 对∀i∈N2,

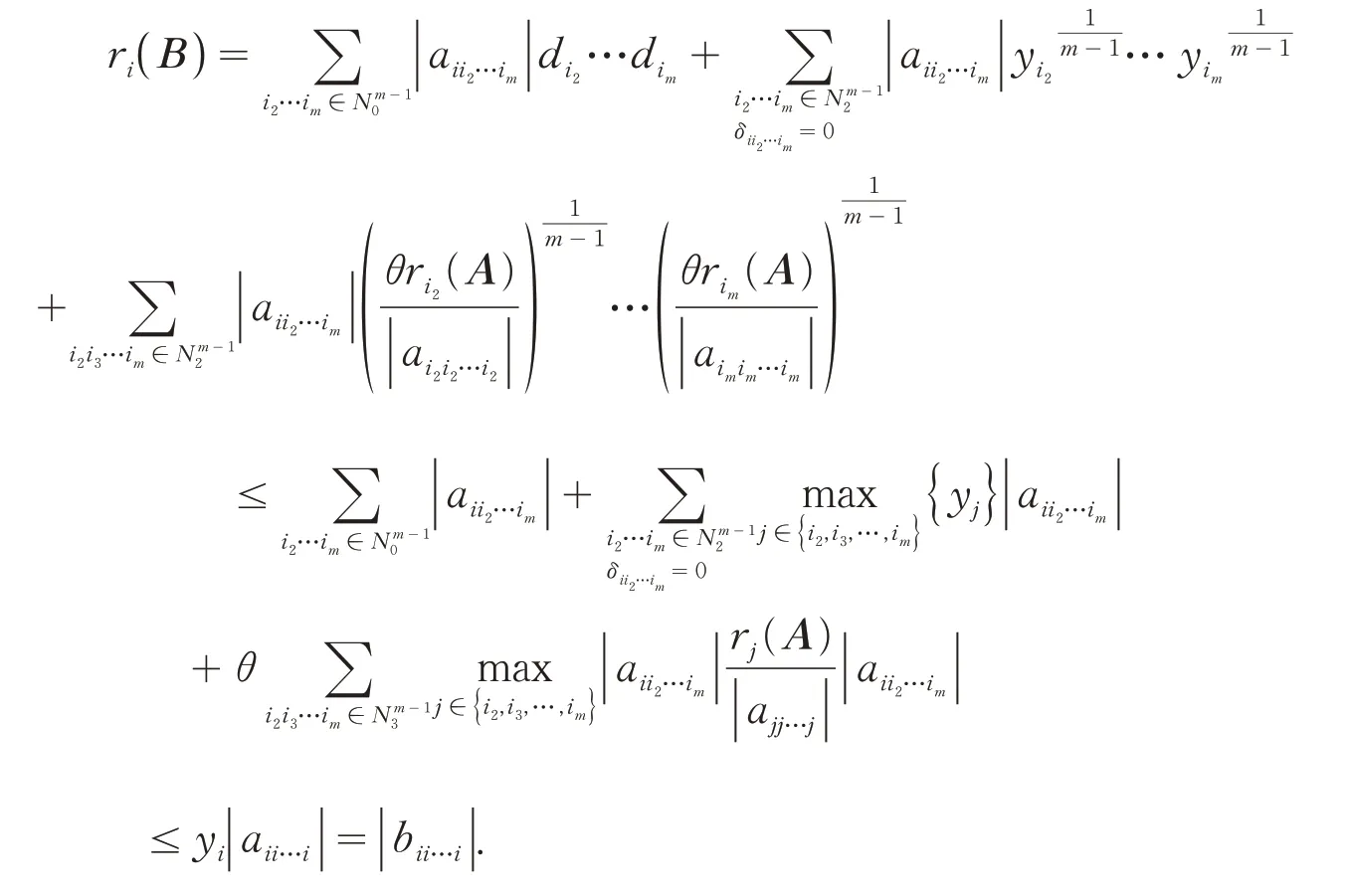
(iii)对∀i∈N3,由θ的定义得:

于是:

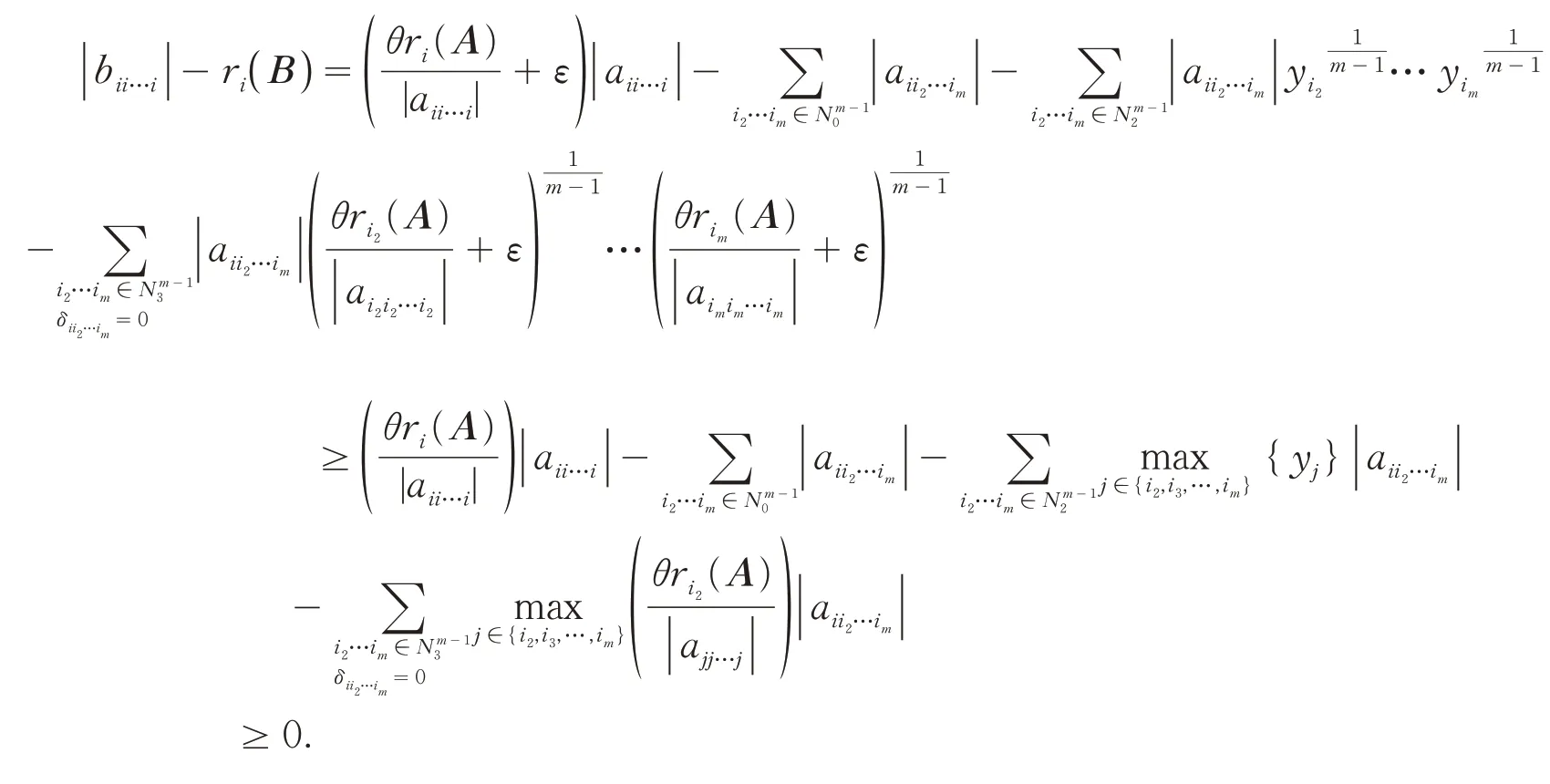
综上可得,|bii…i|≥ri(B)(∀i∈N).又由(6)和(7)式中至少有一个严格不等式成立知存在i0,使得|bi0i0…i0|>ri0(B).由A不可约知B不可约,故由引理3知B是H-张量.进而,由引理2知A是H-张量.

记:

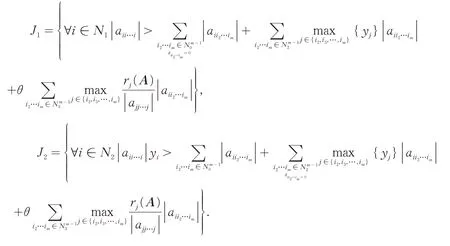
定理3 设A=(ai1i2…im)是m阶n维张量.若:

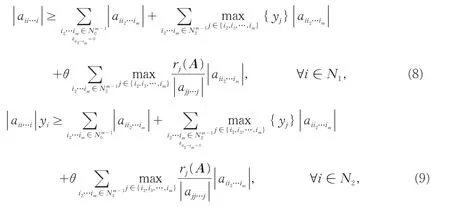
且J1∪J2≠∅,又对任意i∈(N1/J1)∪(N2/J2),A有一条从i到J1∪J2中某一元素j的非零元素链,则A为H-张量.

证明：构造矩阵D= diag(d1,d2,…,dn),记,其中：

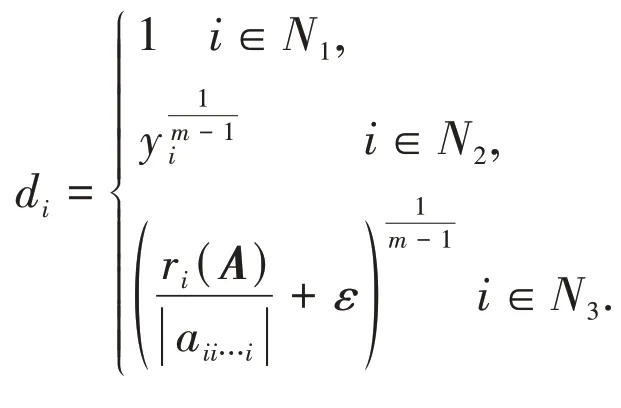
由yi及ε的定义知di< 1(i∈N2∪N3).类似于定理2的证明得|bii…i|≥ri(B)(∀i∈N).

又由J1∪J2≠∅知至少存在一个i0∈N, 使得|bi0i0…i0|>ri0(B). 若|bii…i|=ri(B), 则i∈(N1J1)∪(N2J2),且A有一条从i到J1∪J2中某一元素j的非零元素链.因为B不改变A的非零元素链,因此B有一条从i到J1∪J2中某一元素j的非零元素链,即|bjj…j|>rj(B).由引理4知B是H-张量,再由引理2知A是H-张量.

例1 设A=[A(1,:,:) ,A(2,:,:) ,A(3,:,:) ]是一个3阶3维张量,其中:

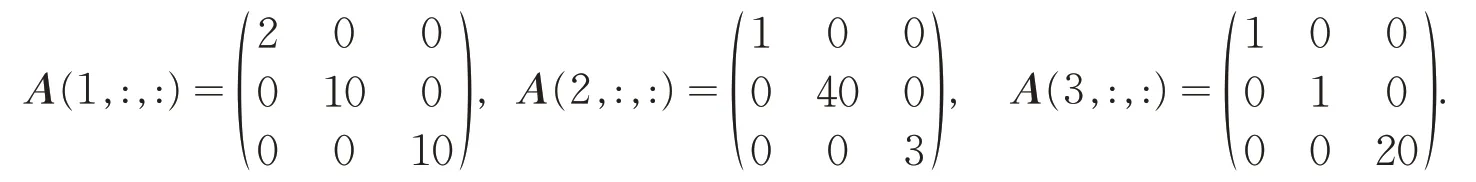
则:

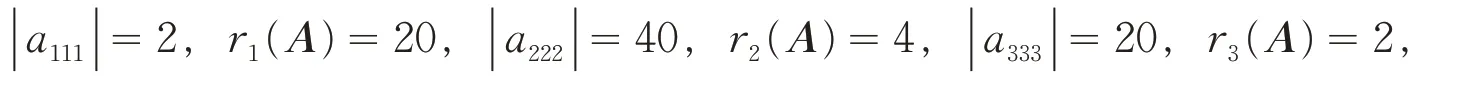
所以N1= ∅,N2= {1},N2= {2,3}.计算得:

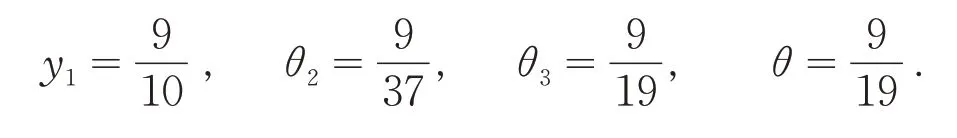
因为:

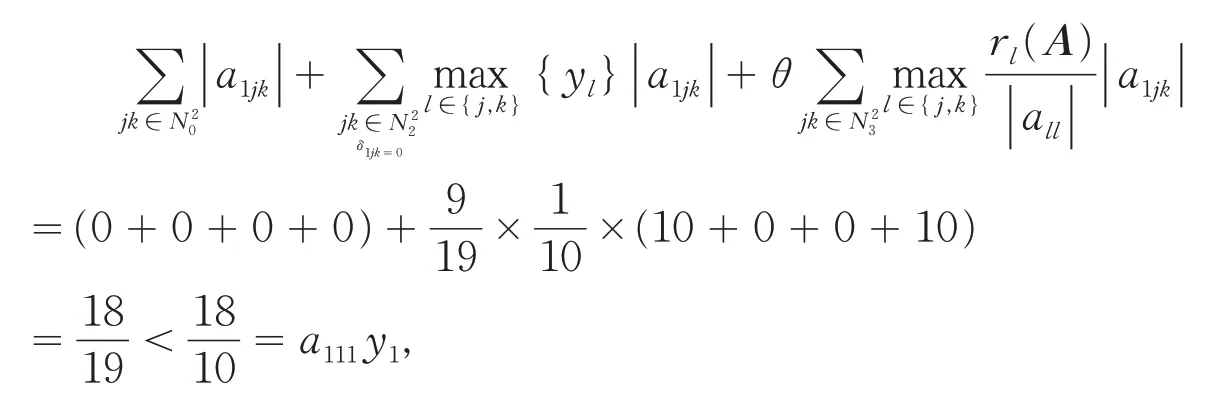
所以张量A满足本文定理1的条件,故张量A为H-张量. 但:

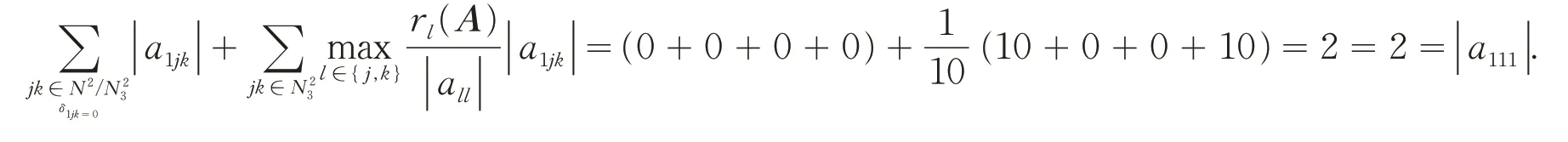
因此A不满足文献[10]中定理1的条件.

3 应用

基于H-张量的新判定不等式,下面给出判定齐次多项式正定性的一些新条件.

引理5,[5]设A=(ai1i2…im)是m阶n维的实对称张量,m是偶数,ai i…i> 0(∀i∈N).如果A是H-张量,则A是正定的.

根据引理5,定理1,定理2,定理3,得到以下结果:

定理4 设m阶n维张量A=(ai1i2…im)为偶数阶实对称张量,且ai i…i> 0(∀i∈N).如果A满足下列条件之一:

(i)定理1的所有条件；

(ii)定理2的所有条件；

(iii)定理3的所有条件；则A是正定的.

例2 设4次齐次多项式:

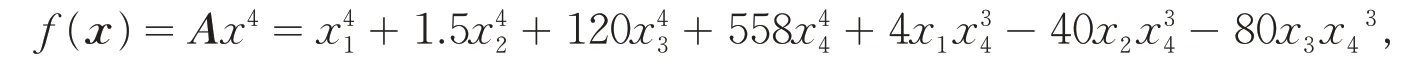
其中A=(ai1i2i3i4)是一个4阶4维实对称张量,且:

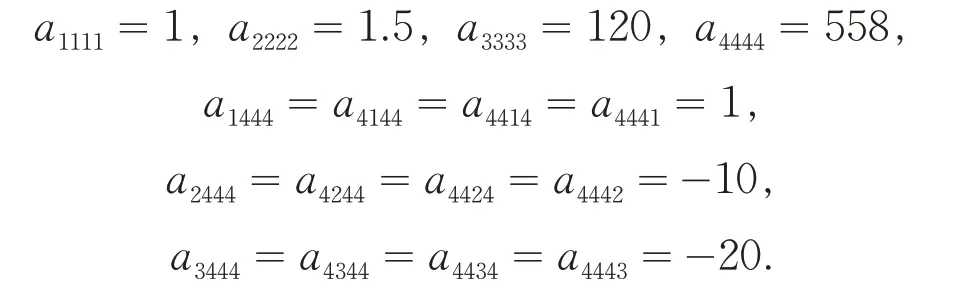
其余的ai1i2i3i4= 0.则:

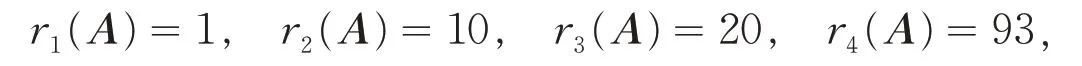
所以N1= {1},N2= {2},N3= {3,4}.计算得:

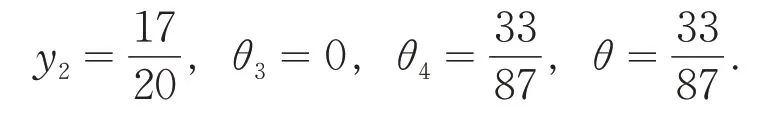
当i= 1时,

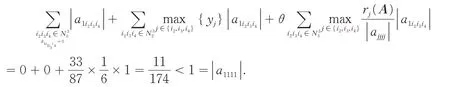
当i= 2时,

因此A满足本文定理1的条件,由定理4知A是正定的,即f(x)是正定的.但:

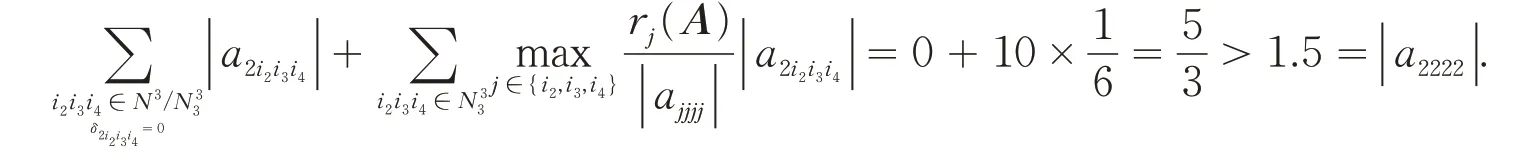
因此A不满足文献[10]中定理1的条件.

本文给出了H-张量新的判别不等式,得到了偶次齐次多项式正定性新的判定条件,并用数值例子表明了新方法的可行性.