基于响应面法的螺纹接头快速连接器分瓣内螺纹片优化设计
伍开宇, 朱海清, 沈 伟, 方 明
(1.江南大学 机械工程学院, 江苏 无锡 214122; 2.嘉兴市计量检定测试院, 浙江 嘉兴 314001)
压力表、真空压力表、真空表及压力变送器等压力计量器具在众多行业中被广泛应用,为了保证其计量性能稳定可靠,需进行定期检定。多数用户采用的方式是将压力计量器具拆下送到计量检定单位进行离线检定。目前国内大多数计量检定设备的连接头多为传统内螺纹接头,压力计量器具离线检定时的安装与拆卸主要依靠扳手,工作人员劳动强度大且工作效率低。而螺纹接头快速连接器采用弹簧按压式可快速连接与拆卸,与传统内螺纹接头相比,其操作简便,灵活性高,可提高检定工作效率同时减轻了检定员工作强度。
螺纹接头快速连接器最高工作压力为16 MPa,其可靠性不容忽视。而分瓣内螺纹片为固定压力计量器具螺纹接头的主要受力部件,工作时分瓣内螺纹片的过大变形会扩大其端面密封间隙导致O形密封圈出现挤隙现象,很可能会导致O形密封圈接触压力达不到要求而密封失效。因此,对其进行结构尺寸参数优化,降低分瓣内螺纹片的结构变形量对于提高螺纹接头快速连接器的运行寿命、可靠性具有重要意义。
1 分瓣内螺纹片结构仿真分析
1.1 螺纹接头快速连接器整体结构
螺纹接头快速连接器结构如图 1 所示,该装置主要由5部分组成,分别是分瓣内螺纹片、按压套筒、内芯、固定底座和密封圈(包括压缩弹簧)组成。其中分瓣内螺纹片是快速连接器的核心部分,由6块沿周向均布的相同分瓣内螺纹片组成,套筒与内芯分别有支撑的压缩弹簧。安装时,螺纹接头按压内芯,分瓣内螺纹片向内闭合,套筒在弹簧的作用下上弹使分瓣内螺纹片抱住螺纹接头,将压力计量器具的螺纹接头稳定地固定在检定设备上,并保证良好的密封性能。拆卸时,按压套筒,套筒下移,分瓣内螺纹片张开,内芯在弹簧的作用下将螺纹接头推出,从而轻松拆卸。
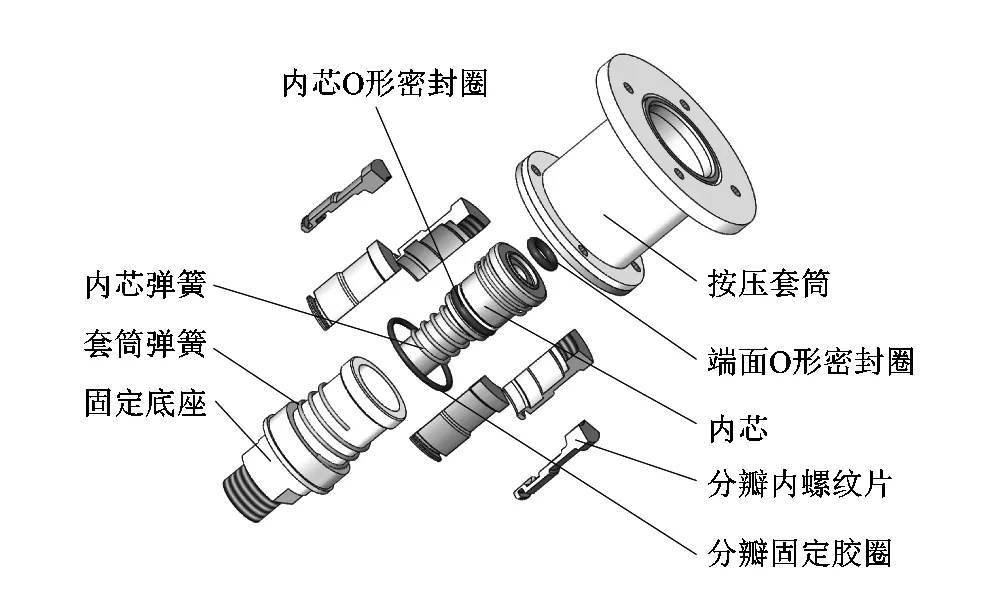
图1 螺纹接头快速连接器爆炸图
1.2 分瓣内螺纹片结构参数模型
分瓣内螺纹片的结构参数如图2所示。由于抓取机构是由6块沿周向均布的分瓣内螺纹片组成,且受力情况相同,所以文中选取其中的一片进行有限元分析。

图2 分瓣内螺纹片参数化模型
1.3 仿真分析
分瓣内螺纹片的材料选用 45号钢,材料属性如表1所示。螺纹接头工作温度为室温,安全系数取1.3;其许用应力[σ]为273 MPa。

表1 45号钢材料属性
将分瓣内螺纹片参数化模型导入ANSYS Workbench软件的 Static Structural 模块,采用六面体网格对其进行网格划分,网格大小设置为0.4 mm,划分完的网格节点数为148 382,单元数为32 946,网格平均质量为95.2%,网格质量较高[1]。
静力学分析模拟极限危险工况,即待检定压力计量器具螺纹接头为M20×1.5、检定压力为16 MPa工况下的分瓣内螺纹片受力情况。内芯受力F为压力产生的推力F1=5 966.00 N加上弹簧产生的推力F2=69.44 N,F为6 035.44 N;内芯受力最终通过螺纹接头传导至分瓣内螺纹片。其中分瓣内螺纹片将螺纹接头压紧在校验座上时,分瓣内螺纹片的内螺纹与接头外螺纹接触,经计算校核内螺纹不会失效,将其简化为受力面平行受力。
对图2中标记面A处施加大小为F/6,方向平行于接触面A向上的力载荷,B面施加固定约束,C面添加圆柱面约束,得到分瓣内螺纹片总变形云图与等效应力云图如图3所示。从图3可以看出分瓣内螺纹片最大变形量为0.027 mm,最大等效应力σmax=265.32 MPa。最大变形量相对于密封间隙0.195 mm而言,变动量为15.3%,因此需对其结构尺寸参数进行优化,减小变形量。

图3 优化前分瓣内螺纹片计算云图
2 基于响应面法的结构优化
响应面法是一种采用试验设计理论对指定的设计点集合进行试验,得到目标函数和约束函数的响应面模型,从而预测非试验点响应值的方法[2-4],具有精度高、周期短、试验次数少且能考虑各设计变量间相互影响趋势等优点。响应面模型的建立包含试验点的选取、拟合函数的选取以及模型合理性评估3个部分[5-8]。
2.1 设计变量的确定
影响快速接头分瓣内螺纹片结构性能的因素很多,在其它条件不变时,选取分瓣内螺纹片上的内螺纹部分厚度l、凹槽深度a、凹槽宽度b、凹槽离底面高度h、内壁半径r、外壁半径R以及成型旋转角度θ为设计变量,研究其对分瓣内螺纹片的弹性变形与等效应力的影响。
2.2 试验设计
试验设计(design of experiment,DOE)作为数理统计的分支之一,其目的是在设计空间选取较少的试验点,在满足统计分析要求的前提下达到缩短试验周期以及降低试验成本的目的[9]。常用的试验设计方法有:全因子试验设计、正交实验设计、BBD设计(box-behnken design)与拉丁方试验设计(Latin square design)等。
试验点的选取作为响应面模型构建的第1步,对响应面的精度有很大影响。其中拉丁方试验设计相较于其他的试验设计方法更具填充性与均匀性,是一种覆盖率高、均衡性好的试验设计方法[10]。
课题组选取分瓣内螺纹片的设计变量个数为7,设计变量的初始值及取值范围如表2所示。其中外壁半径R在设计时有最小尺寸限制为18.5 mm。采用拉丁方试验设计方法可确定仿真计算样本数为79。

表2 设计变量初始值和取值范围
2.3 响应面模型建立
响应面模型采用目前较为常用的二阶多项式表达[11]:
(1)
式中:y(x)为拟合函数;xi和xj为输入设计变量;k为设计变量数;a0,ai,aii和aij为回归系数,回归系数的个数为n。
n的计算公式:
(2)
2.4 模型合理性评估
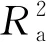
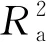
(3)
(4)
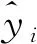
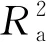
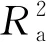
表3 响应面模型的R2值及值
建立的二阶响应面模型的拟合度曲线如图4 所示,通过其可判断二阶响应面模型的预测值与试验设计所取样本点的仿真计算值之间的拟合程度。模型预测的分瓣内螺纹片总质量M、最大变形Dmax与最大等效应力σmax的预测值均分布在y=x直线附近,说明课题组所建立的响应面模型预测值与试验设计所取样本点的仿真计算值具有很好一致性,响应面模型预测能力满足后续对分瓣内螺纹片进一步优化分析的需求。

图4 预测模型拟合度曲线
3 多目标优化
3.1 目标函数和约束条件
分瓣内螺纹片结构优化的目的是提高结构的可靠性。本研究所涉及的优化模型将分瓣内螺纹片结构的最大变形量与最大等效应力的值最小作为优化目标,约束条件为最大等效应力小于材料的许用应力[σ],最大变形量应低于优化前的结构最大变形量0.027 mm。对其建立的多目标优化数学模型如下:
(5)
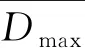
3.2 基于多目标遗传算法求解
传统的多目标优化方法都是将多目标转化为单目标再进行求解,如权重加和法、约束法与理想点法等, 上述优化方法的权重系数均需人为设定,易受主观因素的影响,其优化结果不一定为最优解[13]。多目标遗传算法通过迭代遗传同时对多个目标进行并行处理, 且算法具有很强的鲁棒性, 被公认为最有效的多目标优化算法之一。课题组基于多目标遗传算法对分瓣内螺纹片的多目标优化问题进行求解。
遗传算法的初始样本数量设置为7 000, 每次样本迭代数量设置为1 000。图5为遗传算法经20次迭代后求解的最优Pareto解,从图中可以看出分瓣内螺纹片的最大变形量Dmax与结构质量M是呈负相关的,最大变形量Dmax的减小会伴随着结构质量M的增大。权衡这2个性能指标,课题组重点关注结构最大变形量的优化,故选择算法给出的3组最优解中最大变形量最小的一组解作为分瓣内螺纹片的优化设计方案。
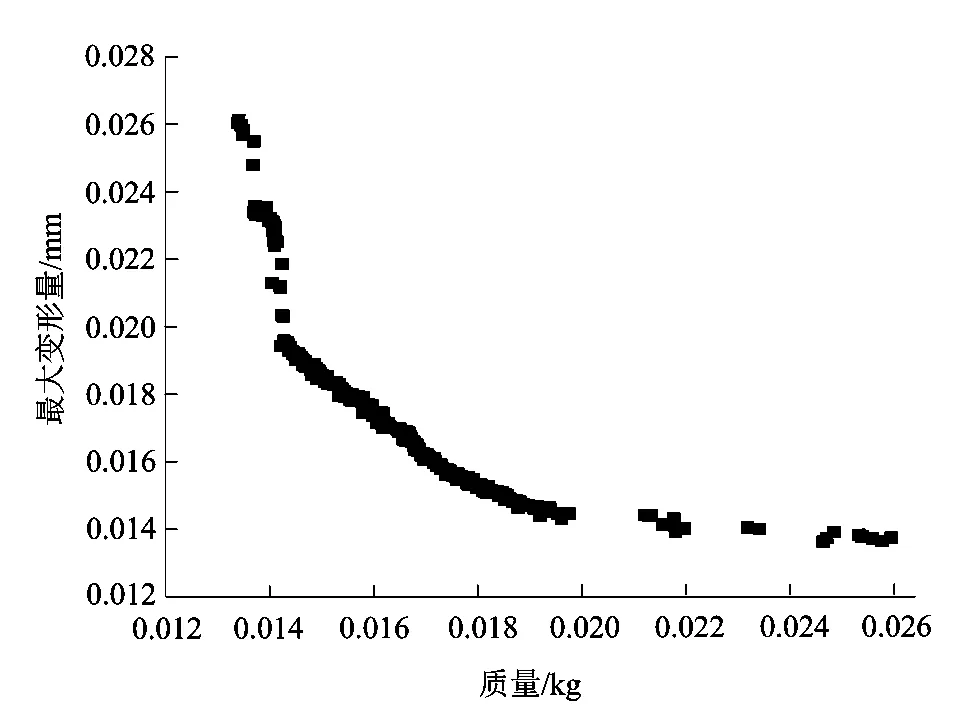
图5 遗传算法最优Pareto解
4 优化结果与分析
为使多目标优化求解所得最优解的尺寸便于实际加工制造,应在其基础上将其修约为一位小数。对输入设计变量与目标参数进行相关性灵敏度分析,根据相关性对尺寸进行修约,从而使结构更贴合预期的优化目标[14]。对于分瓣内螺纹片结构,过大变形将导致O形密封圈的密封间隙增大而出现“挤隙”现象,严重影响螺纹接头快速连接器的密封性能,因此课题组根据图6所示设计变量与结构最大变形量的灵敏度来对各遗传算法求取的最优解进行尺寸修约。
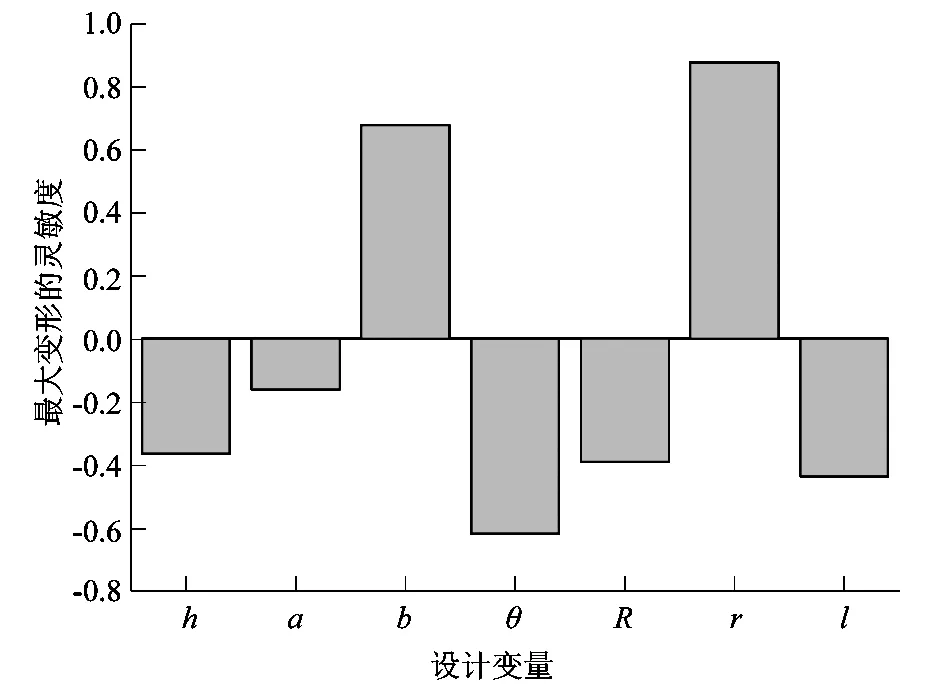
图6 设计变量对最大变形的灵敏度
由图6可知,最大变形与凹槽宽度b、内壁半径r呈正相关;与凹槽离底面高度h、凹槽深度a、成型旋转角度θ、外壁半径R及内螺纹部分厚度l呈负相关。优化前后与对最优解修约后各设计变量值的对比如表4所示。

表4 优化前后设计变量值
优化前后的各目标参数响应值对比如表5所示,从中可以看出分瓣内螺纹片结构最大变形量减小了35.75%,最大等效应力减小了29.7%,总质量仅增大了6.16%。同时从表4可以看出分瓣内螺纹片的各目标参数响应值的变化主要由l,a,b及h的大幅增大与r的小幅减小引起,说明其优化结果一定程度上符合前文所述的灵敏度分析。优化后的分瓣内螺纹片结构的最大变形量Dmax与最大等效应力σmax均大幅降低,结构总质量仅略微增大,分瓣内螺纹片为小尺寸零件,对其质量的大小并无要求,优化效果符合预期目标,验证了本优化方法的可行性。

表5 结构优化前后目标参数响应值对比
根据表4所示的修约后的设计变量值建立分瓣内螺纹片的三维模型并对其进行有限元分析,其最大变形及等效应力云图如图7所示。

图7 优化后结构计算云图
5 结语


