基于七次多项式插值的RRT避障规划

石英男， 胥光申*， 盛晓超

(1.西安工程大学 机电工程学院， 陕西 西安 710048；2.西安工程大学 西安市现代智能纺织装备重点实验室， 陕西 西安 710048)

工业机械臂是机械化和自动化生产加工过程中一种重要的机械设备，在自动化生产过程中通过模拟人的动作抓取和移动物体来完成各项工作，提高劳动生产力[1]。

机械臂避障轨迹规划问题是机械臂研究的重要课题，主要研究当工作空间中存在障碍物的情况下，如何寻找到一条从起始点到目标点的路径。现有的机械臂避障轨迹规划的研究有人工势场法、蚁群算法、栅格法和快速拓展随机树算法RRT等。课题组基于快速拓展随机树RRT算法进行研究，RRT算法是一种通过随机构建空间填充树进行有效搜索的非凸、高维空间算法。相较于基于图的搜索算法，RRT算法最主要的优点就是收敛速度较快，在多自由度机械臂的路径规划问题中发挥着重要作用。

对于关节空间的轨迹规划问题，国内外学者多采用多项式插值法。基于多项式插值法的运行位移、速度和加速度曲线比基于线性插值法的运行曲线更为平稳，机械臂的轨迹精度更高。文献[2]中分析了在工业机器人轨迹规划中采用三、五次多项式的运动性能，结果表明五次多项式的轨迹规划效果优于三次多项式。在实际工程应用中，常采用五次多项式插值法进行关节轨迹规划，该方法的计算量较小，但关节位移变化较大影响了机械臂工作的平稳性[3]。

因此，课题组采用七次多项式对各关节进行轨迹规划。课题组使用MATLAB机器人工具箱对机械臂进行建模以及RRT避障轨迹规划的仿真。研究结果表明：机械臂在运动过程中，各关节角位移、角速度及角加速度随时间变化曲线没有发生突变，机械臂通过RRT算法能够实现平稳的避障运动。

1 六轴机械臂的运动学分析

1.1 机械臂结构及连杆参数

课题组选择了经典的6自由度串联机械臂来进行建模。6自由度串联机械臂由6个关节及6个杆件组成，具有6个关节自由度。根据标准D-H表示法，建立6自由度串联机械臂坐标系如图1所示。6自由度串联机械臂D-H参数如表1所示[4-5]。

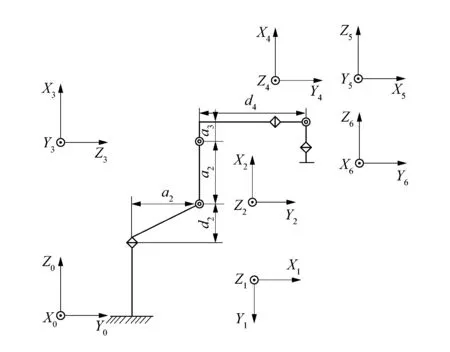
图1 6自由度机械臂坐标系

表1中，关节角θi为从xi-1到xi绕zi的转动角度；距离di为从xi-1到xi沿zi的距离；长度ai为从zi到zi+1沿xi的距离；角度αi为从从zi到zi+1绕xi转动的角度。

表1 6自由度机械臂D-H参数

连杆变换的一般表达式：

(1)

(2)

变换矩阵表示由3个方向向量和1个位置向量组成。向量n，o和a是3个方向向量，表示机械臂末端相对于参考坐标系的方向，如n轴相对于参考坐标系x轴方向表示为nx。第4个向量p是位置向量，向量p表示机械臂末端坐标系的原点相对于参考坐标系的位置，如px表示机械臂末端坐标系的原点在参考坐标系x轴的px处。

1.2 机械臂MATLAB建模

根据机械臂的D-H参数表，使用MATLAB的机器人工具箱Robotics Toolbox对6自由度机械臂进行建模，在Link函数输入连杆参数，再利用SearlLink函数连接各关节建立机械臂[6]，最后得到图2所示的6自由度机械臂的三维模型。

图2 6自由度机械臂仿真模型

2 基于RRT算法的路径规划

2.1 机械臂避障规划

课题组在获取起始点和目标点以及障碍物等环境信息后，通过RRT算法求得路径，利用机器人工具箱将起始点和目标点之间所经过的路径点与时间相对应，将关节变量变换成与时间关系的函数，然后对角速度和角加速度进行约束进而得到机械臂在避障运动过程中的轨迹规划。

2.2 快速拓展随机树RRT算法

RRT算法是一种与树的生长相似的构造方法。在路径规划时，会在状态空间中生成一个随机点，从树中找到距离该随机点最近的位姿点，沿着位姿点到随机点的生长方向，判断随机点是否和障碍物发生碰撞，如不碰撞，将该随机点添加到树中，不断重复，直到最终点附近区域被搜索到为止。RRT算法的流程如图3所示[7]。

图3 RRT算法流程图

RRT算法路径规划的描述：

1) 初始化搜索树。令状态空间中的起始点为搜索树的起点，此时搜索树中只存在根节点Xstart一个节点；

2) 在状态空间中产生一个随机点Xrandom，若该点不在障碍物范围内则计算搜索树中所有节点到点Xrandom的欧式距离，并找到距离最近的节点Xnear，若该点在障碍物范围内则删除点Xrandom并重新生成随机点，重复该过程直至找到最近的点;

3) 生成新节点。在点Xnear和点Xrandom连线方向，由点Xnear指向点Xrandom固定生长距离Growdistance生成一个新的节点Xnew，并判断该节点是否在障碍物范围内，若不在障碍物范围内则将点Xnew添加到搜索树中，否则的话返回步骤2)重新对状态空间进行随机采样；

4) 停止搜索。当点Xnear和目标点Xgoal之间的距离小于某个标准时，将点Xgoal作为搜索树的最后一个节点，退出搜索，算法结束并得到所规划的路径。

2.3 机械臂RRT路径规划

使用MATLAB平台，在三维空间中设定起始点Source=[100,100,10]，设定目标点Goal=[100,-100,10]，在起始点与目标点之间添加障碍物，得到如图4所示的三维空间环境。

图4 三维空间环境

在三维空间中，通过RRT算法建立搜索树如图5所示。

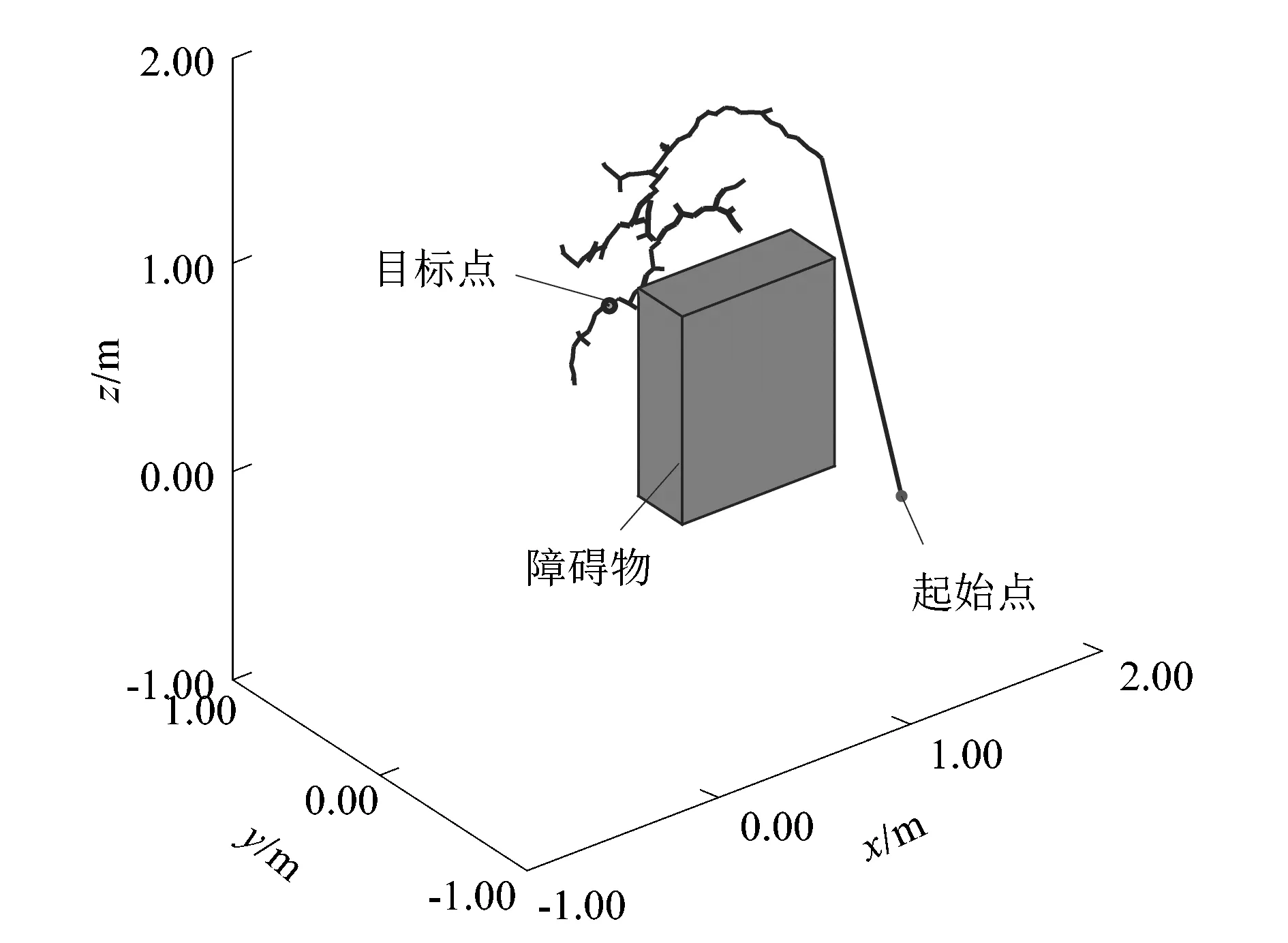
图5 RRT搜索树

根据RRT搜索树得到机械臂的运动路径轨迹如图6所示。

图6 有障碍物的路径轨迹

根据RRT算法得到的路径，使用MATLAB机器人工具箱，通过五次多项式插值法对机械臂进行轨迹规划，得到机械臂的运动过程和各个关节运行曲线如图7～10所示。

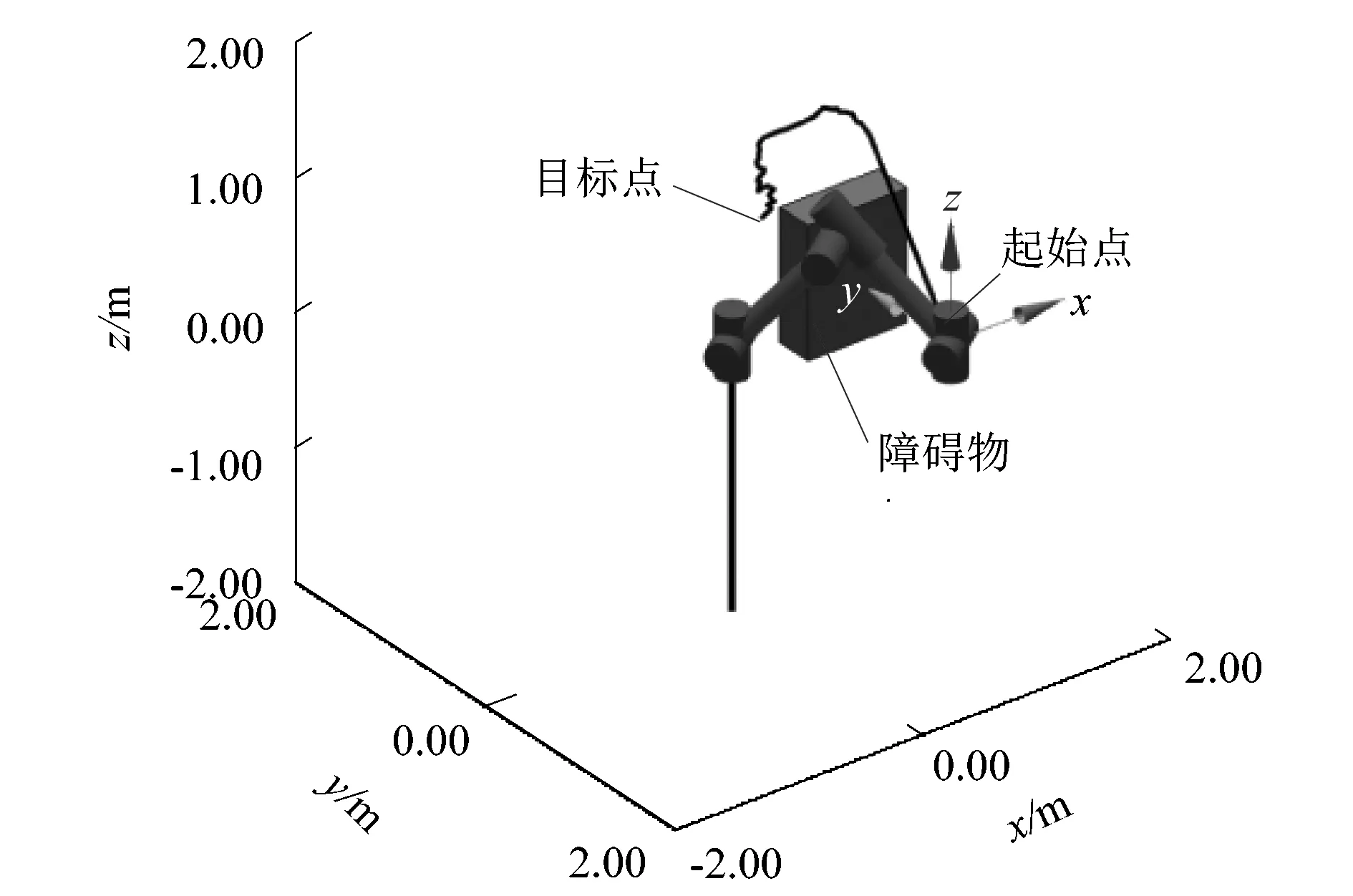
图7 6自由度机械臂避障运动轨迹

图8 各关节角位移曲线

图9 各关节角速度曲线

图10 关节角加速度曲线

从图7中可以看到机械臂从起始点Source开始，沿着轨迹线绕过障碍物，最终达到指定目标点Goal。说明了RRT算法在三维空间进行路径规划的可行性。

仿真结果表明：使用RRT算法在存在障碍物的情况下进行路径规划可以有效的避开障碍物，是一种有效的轨迹规划算法。但是图8中可以明显的看出关节1和关节6的关节位移变化较为明显，各关节的角速度曲线也不够平滑，说明采用五次多项式进行轨迹规划时机械臂的运动平稳性有所欠缺，不满足对作业精度要求较高的场合。为了提高机械臂在避障过程中的作业精度，课题组提出在避障时采用七次多项式插值法来对机械臂进行轨迹规划[8-9]。

3 七次多项式插值的轨迹规划

3.1 七次多项式算法

一般多项式插值法的次数越高其曲线越平滑，但是次数过高会导致插值结果偏离原函数。为了保证计算精度一般最高选取七次多项式插值法进行插值计算。七次多项式插值法规划出的曲线比五次多项式插值法得到的曲线更加平稳连续，机械臂运动性能更高。

采用七次多项式插值法进行关节空间的轨迹规划，设七次多项式：

θt=a0+a1t+a2t2+a3t3+a4t4+a5t5+a6t6+a7t7。

(3)

当时间t=0时：

(4)

当时间t=tm时:

(5)

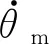
式(3)～(5)可写成如下的矩阵形式：

(6)

公式(6)可简化为θ=Ma。通过计算M-1求出各关节位置，进而求得目标运动轨迹的轨迹方程[10-11]。

3.2 七次多项式插值法避障仿真

本研究中机械臂主要做避障运动，过程较为简单，所以采用点到点运动(point-to-point，PTP)的轨迹规划。之前已经通过RRT算法求得了机械臂的路径，采用七次多项式插值法进行插值计算，并输出其关节角位移、关节角速度和关节角加速度随时间的变化曲线如图11～13所示。

对比图11～13结果和图8～10结果可知，机械臂的各个关节角位移、关节角速度和角加速度的变化更加平滑，这说明采用七次多项式插值法比采用五次多项式插值法的轨迹规划精度更高。

图11 各关节角位移曲线

图12 各关节角速度曲线

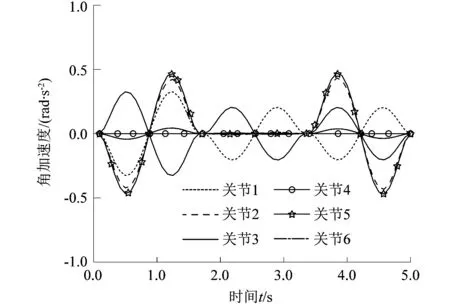
图13 各关节角加速度曲线

较五次多项式插值法来说，七次多项式插值法需要保证角加速度曲线连续，无凸变，其机械臂关节的角加速度轨迹更加平滑，机械臂各关节电机的负载更加稳定，提升了机械臂的作业精度。

五次多项式插值法和七次多项式插值法的优缺点对比如表2所示[12]。

表2 2种多项式插值法的优缺点对比

4 结语

为了提高机械臂在避障过程中作业精度，课题组提出采用七次多项式插值法进行轨迹规划，并在MATLAB平台上进行仿真实验。实验结果表明，对比使用五次多项式插值法的轨迹规划曲线来看，采用七次多项式插值法对机械臂运动进行关节空间轨迹规划时，机器人各个关节运动轨迹更加平滑，关节的角速度不存在突变的问题，关节的角加速度也更加连续，实现了机械臂的稳定运行，提高了机械臂的作业精度，是一种有效的轨迹规划方法。课题组的研究为之后的机械臂避障研究提供了参考，进一步的研究将引入工业以太网EtherCAT作为通信方式进行机械臂控制平台开发，实现对机械臂的避障控制。